Рисунок из параллельных и перпендикулярных прямых (6 видео)

Прямая. Параллельные и перпендикулярные прямые.

Содержание

теория по математике 📈 планиметрия
Обозначения прямой
Признаки параллельности прямых
Аксиома параллельных прямых
Следствия из аксиом параллельных прямых
Перпендикулярные прямые
Урок математики в 6-м классе «Паралелльность прямых»
Презентация к уроку
Перпендикулярные прямые — основные свойства, признаки и правила построения
Основные свойства
Доказательство взаимного расположения
Определение перпендикулярности прямой и плоскости
Построение перпендикуляра
Трехмерное пространство
Четырехмерная система координат и лемма
Применение термина
📹 Видео

теория по математике 📈 планиметрия

Линия, которую изображают на плоскости при помощи линейки, причем, эта линия не должна быть ограничена точкой ни с одной стороны, называют прямой. Другими словами, прямая не имеет ни начала, ни конца.

Обозначения прямой

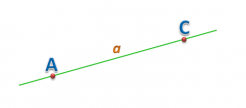
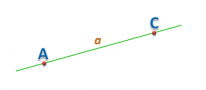
Обычно прямые обозначают прописной латинской буквой или двумя заглавными (если на прямой лежат точки). Рассмотрим это на рисунке. Данную прямую мы можем назвать двумя способами: прямая а; прямая АС.

Рассмотрим теперь две прямые на плоскости. Для них существует два случая расположения: пересекаются и не пересекаются.

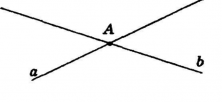
Если две прямые пересекаются, то есть имеют общую точку, то их называют пересекающимися. На рисунке показаны прямые а и b, которые пересекаются в точке A. Запись с помощью символов для данного рисунка выполняют следующим образом: а ∩ b=А, где ∩ — это знак «пересечение».

Если две прямые на плоскости не пересекаются, то их называют параллельными прямыми. На рисунке изображены параллельные прямые. Запись осуществляется следующим образом: a | | b, где | | — знак параллельности.

Признаки параллельности прямых

Рассмотрим прямую с, которая пересекает две прямые а и b и образует с ними восемь углов. Такую прямую с называют — секущая. Пары углов, которые образует секущая, также имеют названия. Итак, на данном рисунке изображены эти все прямые и восемь углов.

Необходимо запомнить названия следующих углов:

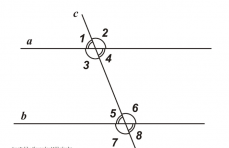
накрест лежащие углы: 4 и 5; 3 и 6;
односторонние углы: 4 и 6; 3 и 5;
соответственные углы: 1 и 5; 3 и 7; 2 и 6; 4 и 8.

С данными углами связаны следующие признаки параллельности прямых:

если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны;
если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;
если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180 0 , то прямые параллельны.

Видео:Эксперт (Короткометражка, Русский дубляж)Скачать

Аксиома параллельных прямых

Вспомним, что аксиомой принято называть утверждения, не требующие доказательств.

Через любые две точки на плоскости проходит прямая и притом только одна.

Аксиома №2 Через точку, не лежащую на данной прямой, можно провести только одну прямую параллельную данной.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Следствия из аксиом параллельных прямых

Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

На данном рисунке видно, что а и b параллельные прямые, с – секущая, она пересекает прямую а в точке А, значит и будет пересекать прямую b в некоторой точке С.

Если две прямые параллельны третьей, то они параллельны.

По данному рисунку видно, что если прямая CD параллельна АВ и прямая MN параллельна АВ, то CD и MN тоже будут параллельны.

Видео:Перпендикулярные прямые. 6 класс.Скачать

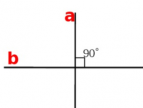
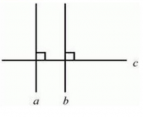
Перпендикулярные прямые

Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.

На рисунке показаны такие прямые а и b. Запись с помощью символов можно сделать следующим образом: а ⊥ b, где « ⊥ » — знак перпендикулярности. Заметим, что две прямые, перпендикулярные к третьей, не пересекаются. На данном рисунке а ⟂ с, b ⟂ c. Видно, что прямые а и b не пересекаются, то есть они – параллельны.

Видео:Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

Урок математики в 6-м классе «Паралелльность прямых»

Презентация к уроку

Образовательные задачи урока:

На основе повторения ранее изученного материала в ходе знакомства с новым создать условия для формирования у учащихся
- понятия параллельных прямых, акцентировав внимание на том, что параллельные прямые лежат в одной плоскости;
- понятий параллельных отрезков и лучей;
- представления о единственности прямой на плоскости, параллельной данной и проходящей через данную точку.
Продолжить формирование навыков работы с инструментами.
Продолжить развитие логического мышления, способностей правильно формулировать мысли в процессе обобщения изученного, работать в группе, отстаивать свою точку зрения.
Развивать критическое мышление.

Воспитательные задачи урока:

Вызвать заинтересованность в изучаемом материале.
Пробудить любознательность.
Возбудить желание решать задачи самостоятельно.
Закрепить уверенность в успехе, достигнутом на уроке в процессе выполнения заданий.

Оборудование: АРМ учителя; каркасные модели многогранников; индивидуальные наборы для конструирования; предметы, поверхность которых похожа на псевдосферу, сферу и другие; рабочие листы к уроку разного уровня сложности (для учащихся 1, 2, 3 уровня обучаемости) (Приложение 3), при этом 6 разных цветов внутри каждого уровня (например, рабочий лист 1 уровня сложности красного, синего, белого, зеленого, желтого, черного цветов)

Продолжительность: 2 урока (можно провести в один день с перерывом, можно разделить на два дня).

Общая цель урока: научить понимать термины, используемые в теме (параллельные прямые, параллельные отрезки, параллельные лучи), находить их на рисунке, строить параллельные прямые разными способами.

Содержание

Деятельность учащихся

Учащиеся 1 уровня обучаемости

Учащиеся 2 уровня обучаемости

Учащиеся 3 уровня обучаемости

Конструирование определения параллельных прямых, отрезков, лучей

Рассмотрите слайды №11, №12.
– Какие геометрические фигуры мы видим на этом рисунке? Какие из них параллельны?

Для получения существенного признака о принадлежности прямых одной плоскости рассматривается слайд №13:

Одновременно со слайдом учащимся демонстрируется каркас куба.
Совместно с учащимися уточняется определение параллельных прямых.

Записывают существенные и несущественные признаки параллельных прямых в рабочий лист

Формулируют определение параллельных отрезков, записывают существенные и несущественные признаки параллельных прямых и параллельных отрезков в рабочий лист

Формулируют определение параллельных отрезков, лучей, записывают существенные и несущественные признаки параллельных прямых, параллельных отрезков и параллельных лучей в рабочий лист

Этап урока

1.Организационный
2. Погружение в тему	Работа со слайдами №2, №3	Делают предположения
	Работа со слайдом №4 Речь на уроке пойдет о прямой. Предлагается слайд №5. Задания: Опишите рисунки. Что общего между ними и в чем различие? Почему? Можно ли объединить какие-нибудь из них? Рассмотрим следующие рисунки: если продолжить стороны трапеции и параллелограмма, то одни прямые пересекутся, а другие – нет. Как можно назвать прямые, идущие рядом?	Разгадывают ребус: *прямая* Отвечают на вопросы: На 1 рисунке – пересекающиеся прямые, на 2 – не пересекающиеся, на 3 – пересекающиеся (перпендикулярные). Общее: на всех рисунках две прямые. Общее: на 1 и 3 рисунках – пересекающиеся прямые, различие: на 2 – не пересекающиеся. Рисунки 1 и 3 можно объединить. Формулируют вывод: прямые могут пересекаться и не пересекаться. Учащиеся делают предположения.
Изучение нового материала	«Рядом идущие» это перевод с греческого языка слова «параллелос». Значит, как можно назвать прямые, которые «идут рядом», то есть не пересекаются?	Делают предположения и приходят к правильному термину: параллельные.
	Работа со слайдами № 6, 7, запись на доске с помощью математического знака	Осмысливают информацию, заполняют лист
	Выполнение заданий, затем проговаривание по слайду № 8	Находят на рисунке параллельные прямые и делают записи в рабочем листе Озвучивают выполненное задание	Находят на рисунке параллельные прямые и отрезки, делают записи	Находят на рисунке параллельные отрезки, прямые, лучи, делают записи
	Приведите примеры параллельных и перпендикулярных прямых из жизни.	Учащиеся приводят примеры, фантазируют по поводу этой проблемы.
	Представьте, что параллельность и перпендикулярность исчезли из нашей жизни, что измениться в мире?
Сообщение о кубизме	Параллельность и перпендикулярность настолько важны, что их не оставили без внимания даже люди, весьма далекие от математики. В начале XX века в живописи зародилось авангардистское направление, характеризующееся использованием геометризованных условных форм, стремлением «раздробить» реальные объекты на стереометрические примитивы. Это направление было названо кубизмом.	Осмысливают получаемую информацию, заносят новые понятия в рабочий лист.
Осмысливают информацию, делают записи	Отвечают на вопросы, корректируют записи	Отвечают на вопросы, корректируют записи
Задание: сформулировать определение параллельных прямых.	Предлагаются варианты ответов, формулируется определение.
Учащимся предъявляется таблица «Параллельные и перпендикулярные прямые» (Приложение 1) и предлагается найти ошибку.	Находят ошибку в отсутствии одного существенного признака
О параллельности каких геометрических фигур можно сформулировать определения?	Формулируют определение параллельности – прямых – отрезков – лучей – прямой и отрезка – прямой и луча – луча и отрезка
Выполнение заданий в рабочих листах	Собирают каркас куба, используя индивидуальные наборы для конструирования, находят параллельные отрезки и делают записи, при необходимости получают помощь учителя	Без сборной конструкции записывают параллельные отрезки, получают каркасные модели других многогранников, находят и записывают параллельные отрезки	Записывают параллельные отрезки, проводят на рисунке другие параллельные отрезки и делают записи (диагонали граней)
Построение параллельных прямых	Найдите решение задачи: как на листе бумаги, на листе фанеры, на земельном участке провести параллельные прямые?	Учащиеся собираются в группы по цвету рабочих листов и решают данную проблему.
	Представление результатов работы групп. Просмотр слайда №16	Предлагаются возможные варианты: с помощью линейки и угольника, с помощью двух угольников, с помощью циркуля и линейки, на земельном участке с помощью доски, трех досок, шпагата и доски и другие варианты.
	Доказательство важности нахождения способов построения и проверки параллельности прямых: зрительные иллюзии.	Рассматривают зрительные иллюзии (гимнастика для глаз).
«Древо знаний»	На доске нарисовано дерево – яблоня, а на ней яблоки трех цветов с написанными на них заданиями трех уровней. Ребятам предлагается «собрать урожай», учитывая, что — «красные яблоки уже созрели» — они висят высоко, сорвать их тяжело – задания на них самые трудные, — «желтые яблоки» — висят ниже, сорвать легче, задания тоже легче, — «зеленые яблоки» — висят совсем низко, поэтому и задания самые простые. Задания на яблоках находятся в Приложении 2. На их выполнение дается определенное время (учитель определяет самостоятельно в зависимости от резервов урока и возможностей класса). Задания заготавливаются в избытке, можно их продублировать, выполняются на карточке, прикрепленной к яблоку (у учеников 1 уровня проверяются на уроке, у 2 уровня по мере возможности, остальные сдаются на проверку, невыполненные и с ошибками разбираются на следующем уроке).	Выполняют задания на яблоках, при необходимости получают помощь учителя	Выполняют задания самостоятельно, при необходимости общаются с одноклассниками	Выполняют задания самостоятельно либо в парах
Историческая справка о евклидовой геометрии	При выполнении заданий вам необходимо было построить прямую, параллельную данной, проходящую через данную точку. Сколько прямых при данных условиях можно провести? Предложение о том, что через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну, было известно еще до н.э. Древнегреческий ученый Евклид называл данное предложение постулатом, и его вместе со всеми известными на тот момент геометрическими предложениями, он описал в «Началах», а геометрия, изложенная в этой книге, называется евклидовой геометрией. Надо отметить, что много сотен лет многие ученые пробовали доказать это предложение (в книге он был под номером 5, поэтому его стали называть пятым постулатом). Внес в это свой вклад и русский математик Н.И.Лобачевский.	Делают вывод на основании выполненной работы о единственности такой прямой, записывают его в рабочий лист.
Историческая справка о Лобачевском и его геометрии	Коля Лобачевский родился 1 декабря 1792 года. Ему не исполнилось еще и 10 лет, когда его отец умер. Осталась его мать, Прасковья Александровна Лобачевская, с тремя малолетними сыновьями. Потребовались ее энергичные усилия, чтобы добиться зачисления сыновей в Казанскую императорскую гимназию на казенный счет. На вступительном экзамене Коле предлагали решить различные математические задачи. Он их решал мгновенно в уме! На просьбу прочитать стихотворение он прочитал «К Мельпомене» Горация и стихотворение М.В.Ломоносова. (Стихотворение входит в программу литературы 5 класса, поэтому учащиеся с ним знакомы, можно предложить процитировать отрывок). Николай учился в гимназии с большим трудолюбием, кроме обязательных – латинского и немецкого – языков, он самостоятельно изучил французский и греческий настолько, что мог читать серьезные книги по математике и философии. В 15 лет он окончил гимназию, а в 24 года уже стал профессором математики. Начался период полного раскрытия незаурядной личности Лобачевского, период изумительно многостороннего и страстного увлечения преподавательской работой профессора, но пятый постулат Евклида ему не давал покоя. Тогда он сделал вывод: пятый постулат недоказуем и от господствовавшего более двух тысяч лет убеждения, что евклидова геометрия есть единственная, необходимо отказаться. Лобачевский создал новую геометрию, но не на плоскости, а на другой поверхности: Есть легенда о том, что он эту поверхность обнаружил в кабинете химии, разглядывая колбу. Из понимания параллельности «по Лобачевскому» вытекает много диковинных на первый взгляд, но строго обоснованных следствий, например, существуют «бесконечные треугольники» и другие удивительные факты, к которым мы обратимся позднее. Открытие Лобачевского было настолько смелым и так сильно опередило развитие математической мысли того времени, что во всем мире почти никто из математиков – его современников – не был готов к восприятию идей воображаемой геометрии. А Фет писал без глаголов, и получалось красиво: Шелест, робкое дыханье, трели соловья. Через 40 лет после дня смерти Лобачевского, перед зданием Казанского университета был установлен памятник великому математику, создателю геометрии, названной в его честь.	В качестве домашнего задания предлагается найти тексты задач, которые предлагали решить Лобачевскому на вступительном экзамене. Цитируют отрывок стихотворения «Случились вместе два астронома в пиру…» Случились вместе два астронома в пиру И спорили весьма между собой в жару. Один твердил: Земля, вертясь, круг Солнца ходит Другой – Земля с собой планеты водит. Один Коперник был, другой слыл Птолемей… Учащимся предлагается прочитать документальный роман Джавада Тарджеманова о Н.И.Лобачевском «Юность Лобачевского (рождение гения)». Учащиеся рассматривают предметы, расположенные на партах, похожие на псевдосферу, шар и другие тела, пробуют провести прямую, параллельную данной через данную точку, делают предположения. Осмысливают получаемую информацию, делают записи
Домашнее задание	Запись домашнего задания, комментарии	Авторы учебника Зубарева И.И., Мордкович А.Г. №148, 149, вопросы на с.43	№ 151, вопросы на стр. 43	№150, вопросы на стр. 43 Десятиминутное эссе «О параллельности»
		Просмотр рабочего листа урока, при необходимости внесение дополнений, корректив Найти тексты задач, предложенных на экзамене Коле Лобачевскому
Рефлексия урока	Сегодня итог урока подведем, поразмыслив в «шести шляпах». Разделимся на шесть групп. Каждая группа получает одну из шести шляп и свои мысли, впечатления и опыт представляет исходя из цвета шляпы. 1 группа – белая шляпа – мыслим фактами, цифрами. Без эмоций, без субъективных оценок. Ответить на вопросы: – Какие новые факты вам стали известны в течение урока? – Кто эти люди и как они связаны друг с другом (слайд 2)? 2 группа – желтая шляпа – позитивное мышление. Необходимо выделить в рассматриваемом материале позитивные стороны и аргументировать, почему они являются позитивными. 3 группа – черная шляпа – противоположность желтой шляпе. Сказать, что было трудно, непонятно, над какими вопросами и заданиями необходимо еще поработать. 4 группа – красная шляпа – эмоциональная шляпа. Нужно связать изменения собственного эмоционального состояния с теми или иными моментами рассматриваемого вопроса. С каким моментом связана та или иная эмоция: грусть, интерес, раздражение, обида, агрессия, удивление, радость и т.д.? 5 группа – зеленая шляпа – творческое мышление. Творческое мышление. Ответьте на вопросы: почему урок носит такое имя? Кто автор стихотворения (слайд 3)? Пофантазируйте, какая геометрия (какие геометрии) могут существовать, кроме евклидовой и геометрии Лобачевского и на каких поверхностях они будут справедливы? 6 группа – синяя шляпа – философская, обобщающая. Распределиться и походить по другим группам, послушать их высказывания, потом собраться и сформулировать выводы, обобщив высказывания всех «шляп».	Учащиеся объединяются в группы по цвету рабочих листов. Ответ на слайде № 31: Евклид – древнегреческий ученый, автор книги «Начала», его именем названа геометрия на плоскости Н.И.Лобачевский – русский математик, создатель новой геометрии М.В.Ломоносов – первый русский ученый – естествоиспытатель, поэт, художник, историк, его имя носит МГУ, автор стихотворения, которое прочитал Коля Лобачевский на вступительном экзамене в Казанскую императорскую гимназию Н.Коперник – польский астроном, создатель гелиоцентрической системы мира, Н.И. Лобачевского называют Коперником в геометрии, а также о нем говорится в стихотворении М.В.Ломоносова Х.Колумб – мореплаватель, испанский адмирал, о нем писал в стихотворении Коля Лобачевский Л.Н.Толстой – русский писатель, учился в Казанском университете, когда Лобачевский там был ректором.
Итог урока	Учитель подводит итог, предлагает к просмотру предпоследний слайд – видеоролик.	Просматривают ролик, осмысливают информацию

Литература: Кордемский Б.А. Великие жизни в математике: Кн. для учащихся 8 – 11 кл. – М.: Просвещение, 1995. – 192

Видео:Построение параллельных прямыхСкачать

Перпендикулярные прямые — основные свойства, признаки и правила построения

В геометрии распространено понятие прямых. Они обозначаются двумя большими латинскими буквами или одной маленькой. При построении линии могут пересекаться и иметь только одну общую точку. Взаимно перпендикулярные прямые находятся относительно друг друга под углом 90°. Построение проводится при применении специальных инструментов.

Видео:Параллельные прямые. 6 класс.Скачать

Основные свойства

При рассмотрении того, какие прямые называют перпендикулярными, нужно уделить внимание свойствам. Они выглядят следующим образом:

Через одну точку А можно провести только одну перпендикулярную линию основному отрезку, остальные линии будут наклонными и могут скрещиваться.

Несколько перпендикуляров никогда не будут между собой пересекаться.

Для обозначения перпендикуляра применяется знак «⊥». В подобном случае угол составляет 90°. На чертеже пересечение обозначается своеобразным квадратом, которые рисуется от двух пересекающихся линий.

Видео:Перпендикулярные прямыеСкачать

Доказательство взаимного расположения

Рассматриваемый термин получил широкое распространение, он фигурирует практически в каждой геометрической задаче. В некоторых случаях о взаимном расположении известно, в других это нужно доказать. Задача доказательства заключается в определении прямого угла между двумя прямыми или плоскостями. Необходимое и достаточное условие перпендикулярности заключается в теореме:

Для определения расположения плоскостей или отрезков относительно друг друга следует провести геометрическое построение. Проходить отрезки должны в одной точке.

Видео:Перпендикулярные и параллельные прямые. Математика 6 классСкачать

Определение перпендикулярности прямой и плоскости

Рассматривая определение перпендикулярных прямых следует учитывать, что подобное свойство применимо к плоскости. Основной признак заключается в перпендикулярности отрезка к любому другому, который находится в плоскости. Перпендикулярность прямых в пространстве указывается определенным знаком.

Доказать перпендикулярность можно проведя геометрические построения. Признаки расположения плоскости и прямой под углом 90° заключаются в следующем:

Отрезки могут быть также параллельными. В этом случае нет точки, в которой будут они пересекаться.

Видео:6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Построение перпендикуляра

Выдержать угловой коэффициент можно различным образом. В большинстве случаев для этого нужно иметь при себе циркуль. Построить перпендикуляр можно следующим образом:

С помощью циркуля проводится построение полуокружности с центром в точке Х. На основном отрезке в результате этого получается две точки А и В. Для отображения полуокружности применяется другой цвет, полученная линия вспомогательная, поэтому не выделяется жирным.

С точки А и В проводится откладывание двух полуокружностей, пересекающихся в двух местах по касательной. Данные точки (P и Q) используются для откладывания линии, которая может пересечь их и основной отрезок с ранее отложенными точками А и В.

Существенно упростить задачу можно путем применения специального чертежного инструмента, к примеру, любого прямоугольного треугольника. Он может называться угольником, основной его признак заключается в наличии двух перпендикулярных плоскостей. Построение проводится следующим образом:

В геометрии чаще всего применяется именно второй способ. Однако первый урок позволяет начертить два взаимно перпендикулярных отрезка с высокой точностью. Недостаток применения циркуля заключается в наличии вспомогательных линий, которые стереть сложно. Написать о взаимном расположении линий можно в описательной записке.

Видео:Перпендикулярные прямые. Практическая часть. 6 класс.Скачать

Трехмерное пространство

В начертательной геометрии линии всегда находятся в двухмерном пространстве. В специальных программах можно начертить отрезки в трехмерном пространстве. Подобное взаимное расположение может выглядеть следующим образом:

Два отрезка перпендикулярны относительно друг друга в случае, если они параллельны другим взаимно перпендикулярным линиям, лежащим в одной плоскости.

Показать правильное взаимное расположение можно путем обозначения угла. Для этого применяются различные способы.

Если две линии лежат в одной плоскости, то они взаимно перпендикулярны при образовании четырех прямых углов.

В жизни подобное расположение прямых встречается крайне часто. Проверить угол можно при применении специальных инструментов.

Видео:Построение параллельных и перпендикулярных прямыхСкачать

Четырехмерная система координат и лемма

Некоторые программы работают с четырехмерным пространством. Взаимное расположение плоскостей под прямым углом в этом случае имеет два смысла: они могут быть перпендикулярны в трехмерном смысле при образовании двугранного угла 90°.

Рассматриваться взаимное расположение плоскостей может и в 4-мерном смысле. Условия выглядят следующим образом:

Они должны пересекаться в точке.

Любые две линии, проведенные в плоскостях через точку пересечения также могут быть перпендикулярными.

Условия четырехмерного пространства определяют то, что через одну точку можно провести 6 взаимно перпендикулярных плоскостей. Определять их взаимное расположение можно несколькими различными способами.

Лемма, касающаяся перпендикулярности, связана с определением параллельности. Если одна из параллельных линий расположена под прямым углом относительно плоскости или отрезка, то вторая также перпендикулярна. Ответ на многие задачи связан с доказательством леммы:

Даны два параллельных отрезка а и b, а также с. Задача заключается в доказательстве b ⊥ c при условии, что a ⊥ c.

Через произвольную точку М проводится третий и четвертый отрезок, которые параллельны прямой а и с. Образующийся угол АМС равен 90°.

Параллельны b и a при условии, что третий дополнительный отрезок параллелен отрезку а. В этом случае он будет параллелен и b.

При соблюдении условий полученный угол будет являться прямым. С учетом проведенных построений можно сформулировать определение перпендикулярности параллельных отрезков.

Видео:Параллельные и перпендикулярные прямые.Скачать

Применение термина

Как ранее было отмечено, встречается большое количество примеров применения рассматриваемого термина. На основе теоремы и доказательства были созданы различные формулы, позволяющие определить протяженность одного из сторон геометрической фигуры.

В средних и старших классах встречается большое количество задач, связанных с определением угла и протяженности сторон построенной фигуры. В некоторых случаях проводится построение диагонали, которая делит 90° на две равные части.

В жизни взаимное перпендикулярное расположение плоскостей встречается крайне часто. Примером служат несущие элементы различных сооружений. Подобное расположение позволяет правильно распределить оказываемую нагрузку. Править наклон можно путем применения специальных измерительных инструментов.

Многие геометрические фигуры построены на основе перпендикулярного расположения отрезков. Наиболее распространен параллелограмм или квадрат, треугольник. За счет выдерживания правильного угла обеспечивается также взаимное параллельное расположение сторон.

Приведенная выше информация указывает на то, что определение угла, под которым расположены плоскости, проводится в самых различных сферах. Инженеры и строители должны с высокой точностью контролировать этот показатель.