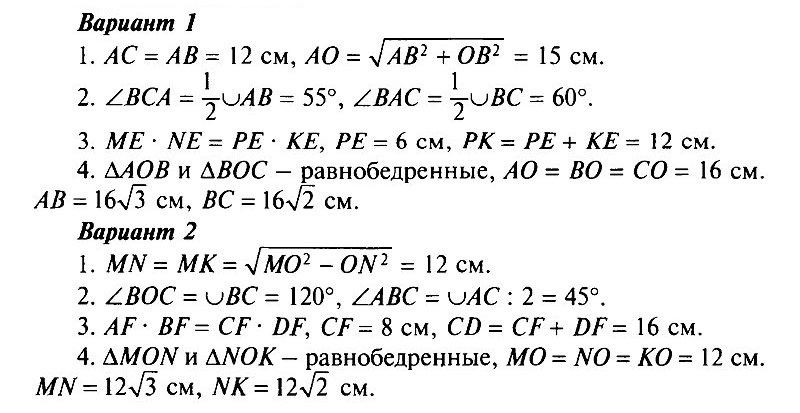Решение задач по теме окружность 8 класс с решением

Подбор задач по теам: Касательная к окружности; центральные и вписанные углы, четыре замечательные точки треугольника. Задачи снабжены рисунками и подробным решением, некоторые задачи представлены в виде «Реши задачу по готовому чертежу». По данным темам также представлены самостоятельные работы в двух вариантах, указаны ответы к ним.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Скачать:

Видео:Геометрия 8 класс : Решение задач. Вписанная окружностьСкачать

Предварительный просмотр:

Окружность. Задачи. Геометрия 8

1. Радиус окружности 5см. Найдите расстояние от центра окружности до прямой, содержащей хорду, равную 8см.

2. Найдите расстояние от точки А до ближайшей к ней точки окружности с центром О радиуса r, если : а) ОА = 12см, r = 8см; б) ОА = 6см, r = 8см.

АВ = ОА — r, АВ = r – ОА,

АВ = 12 – 8 = 4(см) АВ = 8 – 6 = 2(см)

3 . Докажите, что АВ ‹ АС, используя неравенство треугольника.

Имеем ОА‹ ОС + АС

ОВ + АВ ‹ ОС + АС, т.к. ОВ = ОС = r,

Изложить материал в виде небольшой лекции.

1 . , прямая А – секущая.

2. , прямая а имеет с окружностью

одну общую точку.

3 . , прямая а не имеет общих точек

Касательная к окружности. Геометрия 8

1 . Через концы диаметра АВ окружности проведены две касательные к ней. Третья касательная пересекает первые две в точках С и Д. Докажите, что квадрат радиуса этой окружности равен произведению отрезков СА и ВД.

Очевидно, что ∆ СОД — прямоугольный.

, но АС = СК, ВД = КД

(св-во 2-х касательных, проведенных из одной точки к окружности)

2 . Из точки, кратчайшее расстояние которой до окружности равно 25мм, проведена к окружности касательная. Отрезок этой касательной между данной точкой и точкой касания равен 35мм. Найти длину диаметра окружности.

∆ АОВ, В = 90º . По теореме Пифагора:

Ответ : Длина диаметра равна 24 мм.

3 . Из точки, наибольшее расстояние которой до окружности 50мм, проведена к окружности касательная. Отрезок этой касательной между точкой касания и данной точкой равен 40мм. Найти длину диаметра окружности.

∆ АОВ, В = 90º . По теореме Пифагора:

Ответ: Длина диаметра равна 18 мм.

Касательная к окружности. Геометрия 8

1. Дано: R = 5, АВ – касательная.

2 . Дано: АВ – касательная,

Найти: R окружности.

3. Дано: АВ, ВС – касательные,

4. Дано: АВ – касательная,

АО = ОВ, R = 6, АВ = 16

5. Дано: М, Н, К — точки касания

МВ = 4, АК = 5, НС = 8.

1. Прямая КЕ касается окружности с центром в точке О, К – точка касания. Найдите ОЕ, если КЕ = 8см, а радиус окружности равен 6см.

2. В треугольнике АВС АВ = 4см, ВС = 3см, АС = 5см. Докажите, что АВ – отрезок касательной, проведенной из точки А к окружности с центром в точке С и радиусом 3см.

1. Прямая NМ касается окружности с центром в точке О, М – точка касания, , а радиус окружности равен 5см. Найдите NО.

2 . В треугольнике NМК NМ = 6см, МК = 8см, NК = 10см. Докажите, что МК – отрезок касательной, проведенной из точки К к окружности с центром в точке N и радиусом 6см.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Задачи по теме «Окружность 8 класс. Подготовка к ОГЭ по математике»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Окружность 8 класс

Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.

Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.

Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 8.

Точка О — центр окружности, ∠ BOC=160° (см. рисунок). Найдите величину угла BAC (в градусах).

Точка О – центр окружности, ∠ AOB=130° (см. рисунок). Найдите величину угла ACB(в градусах).

Точка О — центр окружности, ∠ BAC=40° (см. рисунок). Найдите величину угла BOC (в градусах).

В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.

На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠ NBA=38 ∘ . Найдите угол NMB. Ответ дайте в градусах.

На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠ NBA=73 ∘ . Найдите угол NMB. Ответ дайте в градусах.

Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ ABC=15 ∘ и ∠ OAB=8 ∘ . Найдите угол BCO. Ответ дайте в градусах.

Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ ABC=56 ∘ и ∠ OAB=15 ∘ . Найдите угол BCO. Ответ дайте в градусах.

Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 84 ∘ . Найдите величину угла OMK. Ответ дайте в градусах.

Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠ C, если ∠ A=75 ∘ . Ответ дайте в градусах.

Точка О – центр окружности, ∠ AOB=84° (см. рисунок). Найдите величину угла ACB(в градусах).

Радиус окружности с центром в точке O равен 85, длина хорды AB равна 80 (см. рисунок). Найдите расстояние от хорды AB до параллельной ей касательной k.

В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 130 ∘ . Найдите вписанный угол ACB. Ответ дайте в градусах.

Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ ABC=25 ∘ . Найдите величину угла BOC. Ответ дайте в градусах.

На окружности с центром O отмечены точки A и B так, что ∠ AOB=66 ∘ . Длина меньшей дуги AB равна 99. Найдите длину большей дуги.

На окружности с центром O отмечены точки A и B так, что ∠ AOB=140 ∘ . Длина меньшей дуги AB равна 98. Найдите длину большей дуги.

Точка О — центр окружности, ∠ BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).

Точка О — центр окружности, ∠ BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).

Четырехугольник ABCD вписан в окружность. Угол ABC равен 70 ∘ , угол CAD равен 49 ∘ . Найдите угол ABD. Ответ дайте в градусах.

Центральный угол AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 7.

Отрезок AB=40 касается окружности радиуса 75 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

Отрезок AB=48 касается окружности радиуса 14 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB =12 , AO =13 .

AC и BD – диаметры окружности с центром O. Угол ACB равен 79 ∘ . Найдите угол AOD. Ответ дайте в градусах.

Касательные в точках A и B к окружности с центром O пересекаются под углом 72 ∘ . Найдите угол ABO. Ответ дайте в градусах.

В угол C величиной 83 ∘ вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.

В угол C величиной 40 ∘ вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.

Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 130°.

Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.

На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.

134. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ ABC=177 ∘ . Найдите величину угла BOC. Ответ дайте в градусах.

Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.

Около трапеции, один из углов которой равен 48°, описана окружность. Найдите остальные углы трапеции.

Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠ C, если ∠ A=9 ∘ . Ответ дайте в градусах.

В окружности с центром O, AC и BD – диаметры. Центральный угол AOD равен 136 ∘ . Найдите вписанный угол ACB. Ответ дайте в градусах.

В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.

В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 10.

Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.

Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB=30, CD=40, а расстояние от центра окружности до хорды AB равно 20.

В трапецию, сумма длин боковых сторон которой равна 22, вписана окружность. Найдите длину средней линии трапеции.

В трапецию, сумма длин боковых сторон которой равна 14, вписана окружность. Найдите длину средней линии трапеции.

Найдите угол ABC. Ответ дайте в градусах.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 987 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 677 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Видео:КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 536 010 материалов в базе

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 25.10.2015
• 526
• 0

• 25.10.2015
• 947
• 0

• 25.10.2015
• 8115
• 39

• 25.10.2015
• 1864
• 39

• 25.10.2015
• 1974
• 0

• 25.10.2015
• 922
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 25.10.2015 21965
• DOCX 111.5 кбайт
• 321 скачивание
• Рейтинг: 3 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Седельникова Галина Дмитриевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 42300
• Всего материалов: 11

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Геометрия 8 класс : Решение задач на центральные и вписанные углыСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Самаре и Тольятти часть школьников перевели на дистанционное обучение

Время чтения: 1 минута

Путин поручил обучать педагогов работе с девиантным поведением

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Школьники в Пензенской области с 7 по 14 февраля уйдут на внеплановые каникулы

Время чтения: 2 минуты

Пермский Роспотребнадзор предписал перевести обучение в школах и ссузах на дистант

Время чтения: 2 минуты

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Решение задач по теме окружность 8 класс с решением

Контрольная работа по геометрии в 8 классе «Окружность» с ответами и решениями (3 уровня сложности по 2 варианта). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 8 класса. ГЛАВА VIII. ОКРУЖНОСТЬ. Урок 66. Геометрия 8 класс Контрольная № 5 по теме «Окружность» (Уровень 1-й, легкий).

Другие варианты контрольной № 5:

Видео:Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Контрольная работа № 5
«Окружность»

Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.

ХОД УРОКА

1. Организационный момент

Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.

2. Выполнение контрольной работы

Контрольная работа № 5
Уровень 1 (легкий). Геометрия 8 класс

Вариант 1

1. АВ и АС — отрезки касательных, проведенные к окружности радиусом 9 см. Найдите длины отрезков АС и АО, если АВ = 12 см.
2. Дано: ∪АВ : ∪BC = 11 : 12 (рис. 8.178). Найти: ∠BCA, ∠BAC.
3. Хорды MN и РК пересекаются в точке Е так, что ME = 12 см, NE = 3 см, РЕ = КЕ. Найдите РК.
4. * Окружность с центром О и радиусом 16 см описана около треугольника АВС так, что ∠OAB = 30°, ∠OCB = 45°. Найдите стороны АВ и ВС треугольника.

Вариант 2

1. MN и МК — отрезки касательных, проведенные к окружности радиусом 5 см. Найдите MN и МК, если МО = 13 см.
2. Дано: ∪АВ : ∪АС = 5 : 3 (рис. 8.179). Найти: ∠BOC, ∠ABC.
3. Хорды АВ и CD пересекаются в точке F так, что АF = 4 см, BF = 16 см, CF = DF. Найдите CD.
4. * Окружность с центром О и радиусом 12 см описана около треугольника MNK так, что ∠MON = 120°, ∠NOK= 90°. Найдите стороны MN и NK треугольника.

3. Рефлексия учебной деятельности

В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.
Домашнее задание: решить задачи, с которыми ученик не справился.

Ответы на контрольную работу
I уровня сложности

Критерии оценивания результатов контрольной работы

• оценка «5» — правильно решены четыре задачи;
• оценка «4» — правильно решены три задачи или правильно решены две задачи, а при решении двух других задач допущены ошибки;
• оценка «3» — правильно решены две задачи или правильно решена одна задача, а при решении двух других задач допущены ошибки;
• оценка «2» — правильно решено менее двух задач.

За правильно решенную дополнительную задачу (№ 5) ставится дополнительная оценка.

Вы смотрели: Геометрия 8 класс Контрольная № 5. Поурочное планирование по геометрии для 8 класса. УМК Атанасян (Просвещение). Урок 66. Контрольная работа № 5 по теме «Окружность» (Уровень 1, легкий) + ОТВЕТЫ и РЕШЕНИЯ.

Другие варианты контрольной № 5:

В учебных целях использованы цитаты из учебного пособия «Поурочные разработки по геометрии. 8 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

🎬 Видео

Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Решение задач по теме: "Окружность"Скачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

8 класс. Решаем задачи на центральные и вписанные углы | Часть 1Скачать

ГЕОМЕТРИЯ 8 класс: Решение задач. Описанная окружностьСкачать

Геометрия 8 класс: Решение задач на касательную к окружностиСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

ОКРУЖНОСТЬ радиус окружности ЗАДАЧИ 8 класс АтанасянСкачать

Решение задач по теме "Окружность". Часть 1Скачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Задача на окружности из ОГЭ-2023!! Разбор за 30 секСкачать

Решение задач на тему "Подобные треугольники". 8 классСкачать