Решение задач касательная к окружности 8 класс с решением (5 видео)

Решение задач касательная к окружности 8 класс с решением

Репетитор
по алгебре

Касательная к окружности .

Касательная к окружности перпендикулярна радиусу

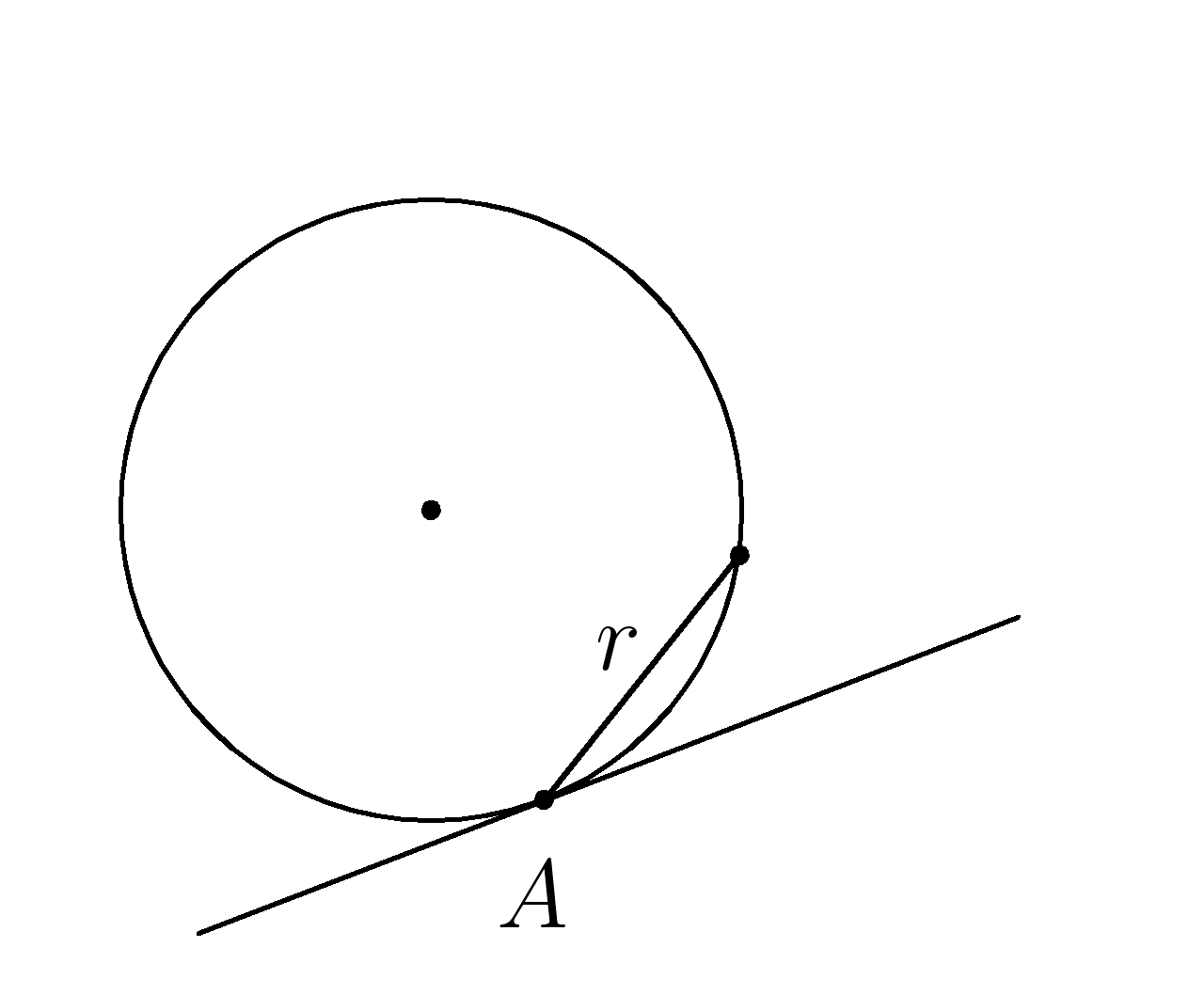
4. Через точку (A ) окружности проведены касательная и хорда, равная радиусу окружности. Найти угол между ними.
Показать ответ Показать решение Видеорешение

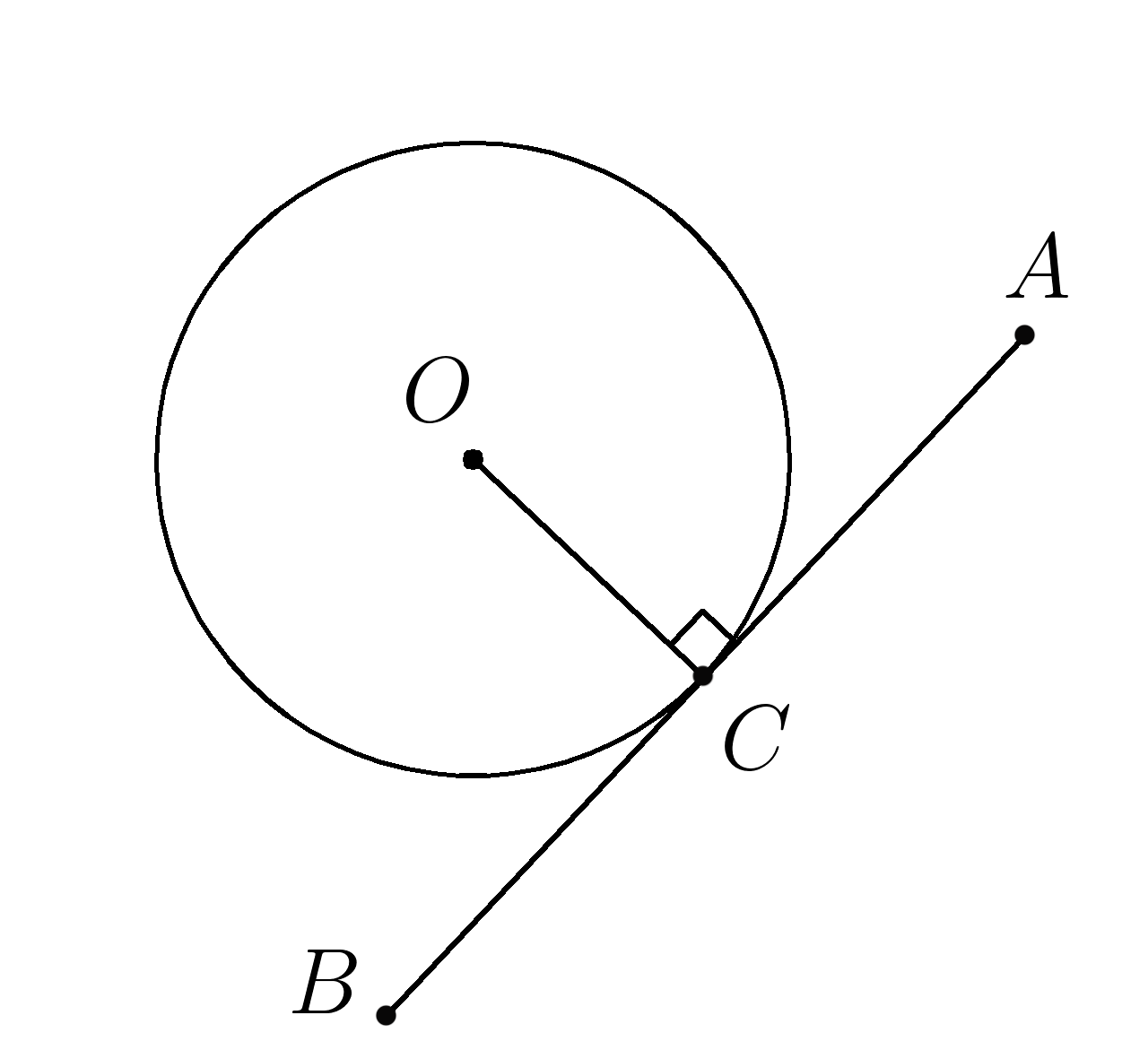
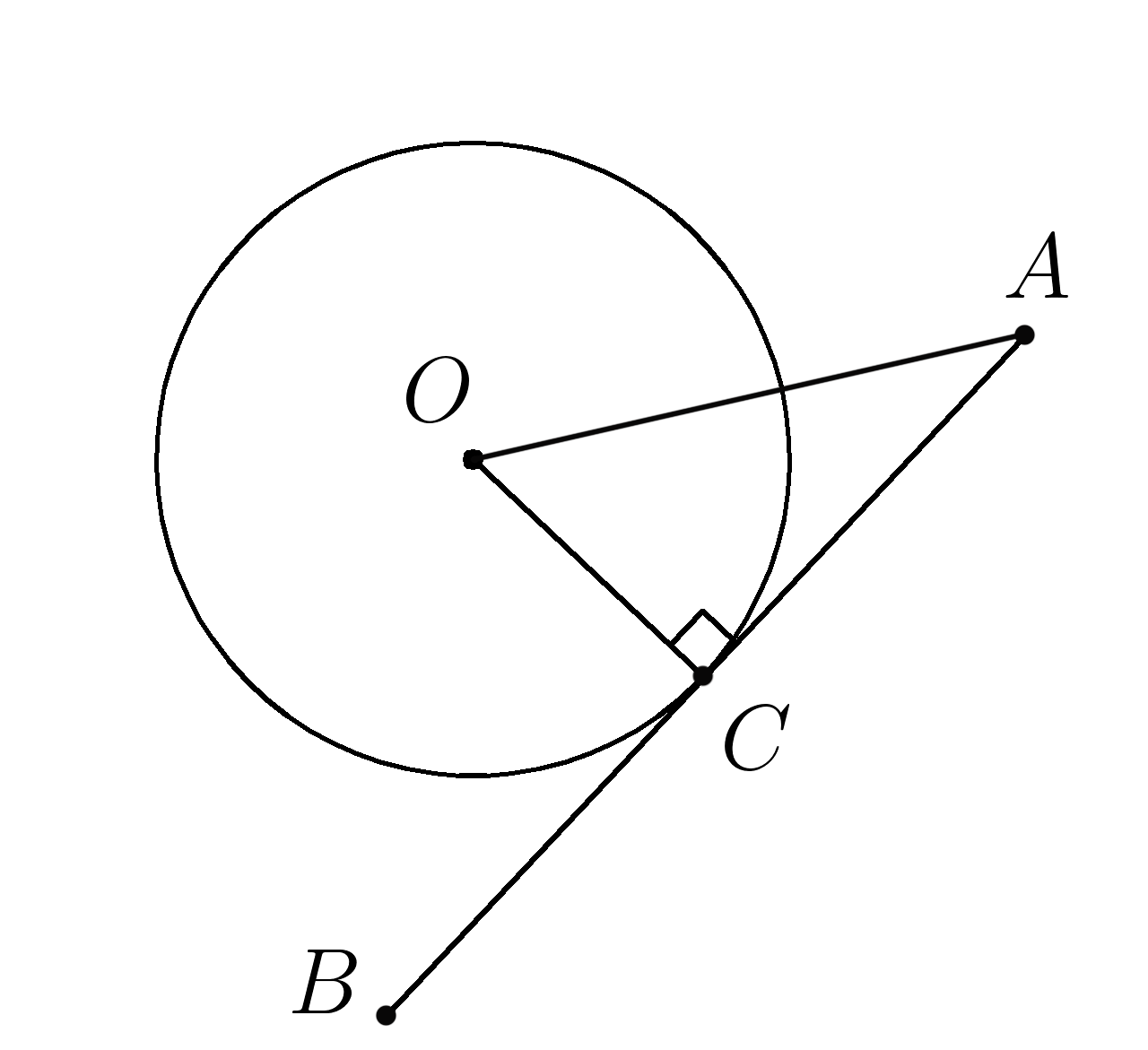
Дано: (AB ) касательная, ( AC ) хорда
(AC=r )
Найти: ( angle CAB )

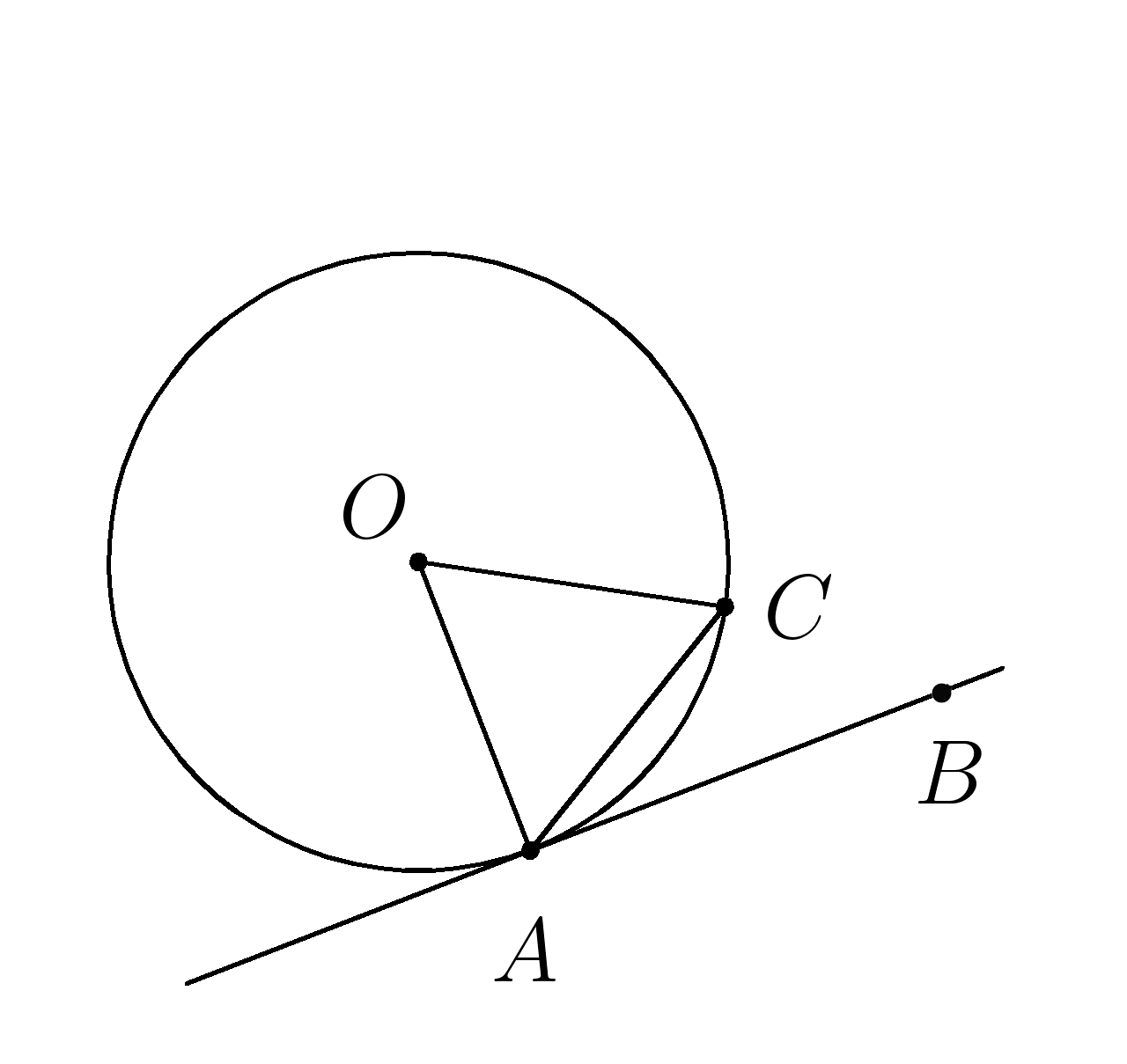
(OA ) радиус
(AB perp OA ) Т.к касательная перпендикулярна радиусу в точке касания

Треугольник (OAC ) равносторонний т.к каждая его сторона равна радиусу

Каждый угол равностороннего треугольника равен (60^0 )

(angle CAB=angle OAB-angle OAB =90^0-60^0=30^0 )

Ответ: ( angle CAB= 30^0 )

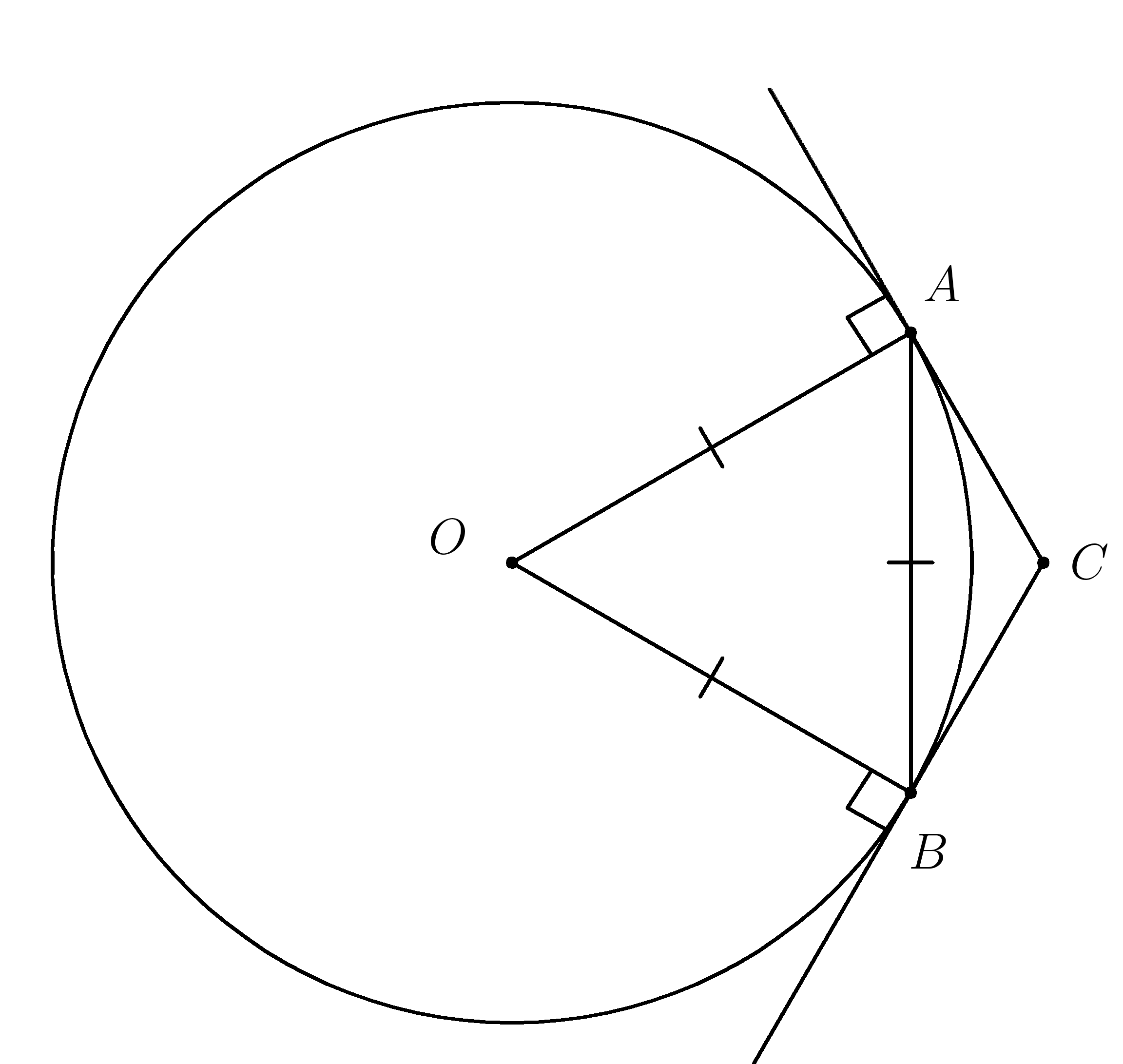
5. Через концы хорды (AB), равной радиусу окружности, проведены две касательнае, пересекающиеся в точке (C ). Найти угол (ACB)
Показать ответ Показать решение Видеорешение

Ответ: (angle ACB=120^0 )

Дано: (AB=OB=OA )
Найти: ( angle ACB )
( angle OBC=90^0 ;;;;;;;;;;; angle OAC=90^0 )

( angle OBA= angle OAB=60^0) (так как ( Delta OBA ) равносторонний )

( angle ABC=angle OBC-angle OBA=90^0-60^0=30^0 )

( angle BAC=angle OAC-angle OAB=90^0-60^0=30^0 )

(angle BAC+angle ABC+angle ACB=180^0 )

Содержание

Касательная к окружности. Решение задач
Просмотр содержимого документа «Касательная к окружности. Решение задач»
Решение задач по теме «Касательная к окружности». методическая разработка по геометрии (8 класс) на тему
Скачать:
Предварительный просмотр:
🎦 Видео

Видео:КАСАТЕЛЬНАЯ к ОКРУЖНОСТИ 8 класс геометрия АтанасянСкачать

Касательная к окружности. Решение задач

Просмотр содержимого документа
«Касательная к окружности. Решение задач»

8 класс. Геометрия

Решение задач по теме «Касательная к окружности»

Учитель математики: Барсукова И.Е.

Повторение теоретического материала

Как вы думаете, сколько общих точек могут иметь прямая и окружность?

r две общие точки одна общая точка не имеют общих точек Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку . Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки . Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек . » width=»640″

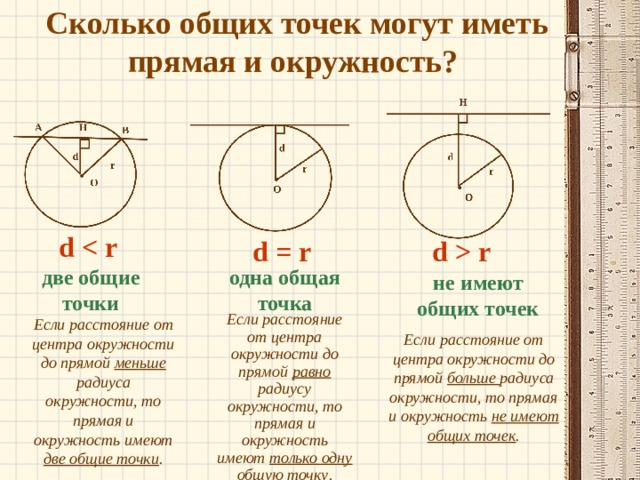
Сколько общих точек могут иметь прямая и окружность?

две общие точки

одна общая точка

не имеют общих точек

Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку .

Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки .

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .

Касательная к окружности

Определение: П рямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

m – касательная к окружности с центром О

М – точка касания

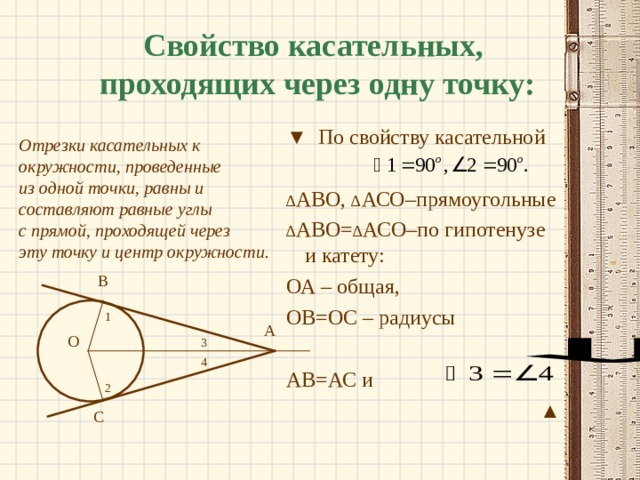
Свойство касательных, проходящих через одну точку:

Отрезки касательных к

из одной точки, равны и

составляют равные углы

с прямой, проходящей через

эту точку и центр окружности.

▼ По свойству касательной

∆ АВО= ∆ АСО–по гипотенузе и катету:

Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она является к асательной.

окружность с центром О

m – прямая, которая проходит через точку М

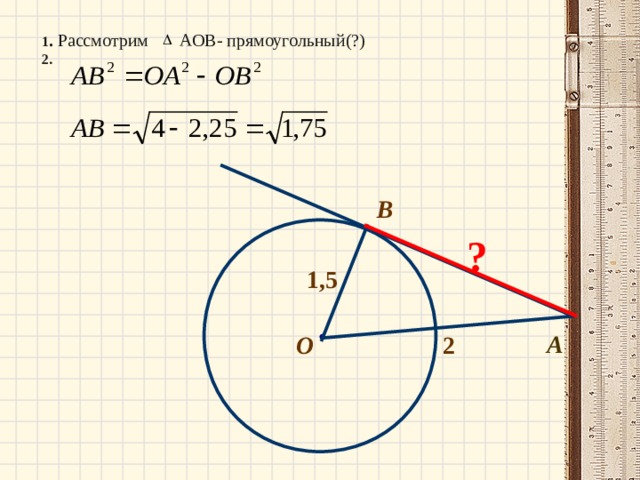
1 . Рассмотрим АОВ- прямоугольный(?)

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Решение задач по теме «Касательная к окружности».
методическая разработка по геометрии (8 класс) на тему

Данная разработка урока систематизирует знания учащихся по теме «Касательная к окружности»

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Скачать:

Вложение	Размер
kasatelnayak_okruzhnosti.docx	518.17 КБ

Видео:Решение задач Касательная к окружностиСкачать

Предварительный просмотр:

Дата: 15.03.18-8А,В 17.03.18-8Б

УМК: геометрия 7 – 9 класс Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др.

Тема урока: Градусная мера дуги окружности . Решение задач по теме касательная к окружности.

Тип урока: Урок получения новых знаний и умений

Цели: Образовательные: Ввести понятие дуги окружности.

Развивающие: развитие математического и общего кругозора, мышления и речи, внимания и памяти; формирование умений применять приемы наблюдения, сравнения, анализа;

Воспитательные: воспитание интереса к геометрии и ее приложениям, активности, общей культуры.

Оборудование: учебник, доска, чертежные инструменты

I. Организационный момент

Сообщить тему урока, сформулировать цели урока.

П. Актуализация знаний учащихся

(Три ученика готовятся у доски.)

— Сформулируйте и докажите теорему о свойстве касательной.

— Сформулируйте и докажите теорему о свойстве отрезков касательных к окружности, проведенных из одной точки.

— Сформулируйте и докажите теорему, обратную теореме о свойстве касательной.

Проверка домашнего задания (готовит ученик у доски)

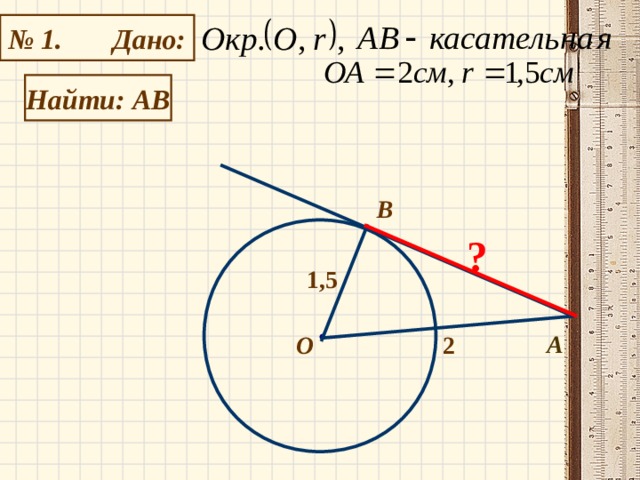
Прямая АВ касается окружности с центром О радиуса r в точке В . Найдите АВ, если АОВ = 60°, а r = 12 см.

∆АОВ- прямоугольный, А = 90° — О = 30° => ОВ = ОА => ОА = 24 см.

По теореме Пифагора АВ = (см). Ответ: (см).

— Каково взаимное расположение касательной АВ и радиуса ОВ.

— Как найти катет АВ треугольника АОВ?

Далее можно заслушать учащихся, подготовивших у доски доказательства теорем.

Решение задач на готовых чертежах

(Самостоятельно с последующей проверкой по готовым ответам.)

Рис. Дано: К = 5, АВ- касательная.

Рис. Дано: АВ — касательная; АВ = 12, ОВ = 13.

Найти: R окружности.

Рис. Дано: АВ, ВС — касательные, ОВ = 2, АО = 4.

Рис. Дано: АВ — касательная, R = 6, АО = ОВ.

5 . Рис. Дано: М, М, К -точка касания.

ОТВЕТ: P ABC = 34.

6 . Рис. Дано: АВ = 10 см, О — центр окружности, СD — касательная, АЕ || СD. Найти: ОС.

ОТВЕТ: ОС = .

III. Решение задач

1. Самостоятельно решить задачи № 641, 644, 647, записав краткое решение (учитель в это время оказывает индивидуальную помощь менее подготовленным учащимся).

Отрезки АВ и АС являются отрезками касательных к окружности с центром О , проведенными из точки А. Найдите угол ВАС, если середина отрезка АО лежит на окружности.

Краткое решение (см. рис.):

В ∆ ОАС С = 90°, ОС = ОА => ОАС = 30° => ВАС = 60°.

Прямые МА и МВ касаются окружности с центром О в точках А и В . Точка С симметрична точке О относительно точки В. Докажите, что АМС = 3 ВМС.

Краткое решение (см. рис. ):

МА и МВ — отрезки касательных, проведенных из точки М => 1 = 2 . Точки О и С симметричны относительно точки В => ОВ = ВС и О, В, С лежат на одной прямой => ∆ OMB = ∆ СМВ по двум катетам => 2 = 3 => АМС = 3 ВМС.

Отрезок АН — перпендикуляр, проведенный из точки А к прямой, проходящей через центр О окружности радиуса 3 см. Является ли прямая АН касательной к окружности, если: а) ОА = 5 см, АН = 4 см; б) НАО = 45°, ОА = 4 см; в) НАО= 30°, ОА = 6 см?

Краткое решение (см. рис.):

а) ОА = 5 см, АН = 4 см => ОН = = 3 см = r => АН — касательная к окружности.

б) HОA = 45°, ОА = 4 см => ОН = НА, ОН 2 + НА 2 = ОА 2 =>2 ОН 2 = 16 => ОН = см 3 см => АН является касательной к окружности.

в) HОA = 30°, ОА = 6 см => OH = OA = 3 см = r => АН — касательная к окружности.

Ответ: а) да; б) нет; в) да.

IV. Самостоятельная работа

К первой задаче из самостоятельной работы записать краткое решение (можно на рисунке); ко второй задаче — полное решение.

1. Прямая КЕ касается окружности с центром в точке О, К— точка касания. Найдите ОЕ, если КЕ = 8 см, а радиус окружности равен 6 см.

2. В треугольнике АВС АВ = 4 см, ВС = 3 см, АС = 5 см. Докажите, что АВ — отрезок касательной, проведенной из точки А к окружности с центром в точке С и радиусом, равным 3 см.

1. Прямая МN касается окружности с центром в точке О, М- точка касания, МNО = 30°, а радиус окружности равен 5 см. Найдите N0.

2. В треугольнике МNК МN = 6 см, МК = 8 см, NК = 10 см. Докажите, что МК — отрезок касательной, проведенной из точки К к окружности с центром в точке N и радиусом, равным 6 см.

1. АВ и ВС — отрезки касательных, проведенных к окружности с центром О и радиусом, равным 10 см. Найдите ВО, если АОС = 60°.

2. Докажите, что основание АС равнобедренного треугольника АВС является касательной окружности с центром в точке В и радиусом, равным медиане треугольника, проведенной к его основанию.

1. МN и NК — отрезки касательных, проведенных к окружности с центром О, MNК = 90°. Найдите радиус окружности, если ОN= 2 см.

2. Докажите, что стороны равностороннего треугольника касаются окружностей, проведенных с центрами в его вершинах и радиусами, равными любой из его биссектрис.

1. ЕК и ЕF — отрезки касательных, проведенных к окружности с центром О и радиусом, равным 6 см, КОF = 120°, А — точка пересечения КF и ОЕ. Найдите ОА и АЕ.

2. Даны угол и отрезок. Постройте окружность радиусом, равным данному отрезку, касающуюся сторон данного угла.

1. РМ и РN — отрезки касательных, проведенных к окружности с центром О и радиусом, равным 10 см, МОN= 120°, Е — точка пересечения МN и ОР. Найдите ОЕ и РЕ.

2. Даны угол и отрезок. Постройте окружность, касающуюся сторон данного угла, с центром, удаленным от вершины угла на расстояние, равное длине данного отрезка.

4. Изучение нового материала (в плане учебника стр. 167)