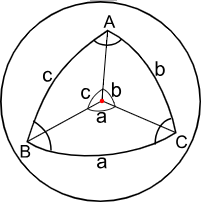
Сферические треугольники.

Свойства сферических треугольников.
Каждая сторона и угол сферического треугольника по определению меньше 180°. Геометрия на поверхности шара является неевклидовой; в каждом сферическом треугольнике сумма сторон заключена между 0 и 360°, сумма углов заключена между 180° и 540°. В каждом сферическом треугольнике против большей стороны лежит больший угол. Сумма любых двух сторон больше третьей стороны, сумма любых двух углов меньше, чем 180° плюс третий угол.
Сферический треугольник единственным образом определяется (с точностью до преобразования симметрии):
- тремя сторонами,
- тремя углами,
- двумя сторонами и заключенным между ними углом,
- стороной и двумя прилежащими к ней углами.
Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Решение прямоугольных и четвертных сферических треугольников
Прямоугольные и четвертные сферические треугольники являются частным случаем косоугольных сферических треугольников.
Прямоугольным сферическим треугольником называется такой сферический треугольник, у которого один из углов равен 90°.
Четвертным сферическим треугольником называется такой сферический треугольник, у которого одна из сторон равна 90°.
К этим треугольникам применимы все правила и алгоритмы решения косоугольных сферических треугольников.
Прямоугольные треугольники можно решать по основным формулам сферической тригонометрии. Так как один из углов равен 90°, формулы значительным образом упрощаются (sin(90°)=1, cos(90°)=0) и состоят, как правило, из двух множителей. Но более рационально производить решение по правилам Модюи-Непера, почти полностью исключающим промежуточные преобразования, а значит и ускоряющим решение (
Пример 3.2).
Правила Модюи-Непера формулируются следующим образом:
1) В прямоугольном сферическом треугольнике косинус любого среднего элемента равен произведению котангенсов крайних смежных с ним элементов.
2) Косинус отдельно лежащего элемента сферического треугольника равен произведению синусов двух не смежных с ним рядом лежащих элементов.
В обоих правилах принято, что катеты лежат рядом друг с другом и вместо катетов надо брать их дополнения до 90°.
Формул такого вида 10. Все они однотипны, поэтому для примера приведём четыре характерных:
|

cos a = ctg B ctg C
cos B = ctg a ctg (90° – c)
| |
 |
cos (90° – c) = sin C sin a
cos a = sin (90° – b) sin (90° – c)
Следовательно, в задаче на прямоугольный треугольник, надо задать два элемента и указать, какой угол равен 90°.

1) Выполняем схематический чертёж и помечаем данные и искомые элементы.
2) Подбираем необходимые формулы.
(по основным формулам сферической тригонометрии)
A, B – формула котангенсов;
c – формула косинуса стороны;
1. ctg A sin C = ctg a sin b – cos b cos C
2. ctg B sin C = ctg b sin a – cos a cos C
3. cos c = cos a cos b + sin a sin b cos C
3) Преобразовываем формулы и производим анализ на знаки. После преобразований независимо от первоначальных формул результат одинаков.
ctg A = ctg a sin b
ctg B = ctg b sin a
cos c = cos a cos b
(по правилам Модюи-Непера)
cos (90 – a) = ctg B ctg (90 – b)
cos (90 – b) = ctg A ctg (90 – a)
cos c = sin (90 – b) sin (90 – a)
ctg A = ctg a sin b
ctg B = ctg b sin a
cos c = cos a cos b
Не забываем, что отношение, это разность логарифмов
lg sin A = 9.76234 lg sin B = 9.99528 lg sin С =10,00000



0,00971 0.00971 0.00971
Четвертные сферические треугольники, как и прямоугольные можно решать по основным формулам сферической тригонометрии. Т.к. одна из сторон равна 90°, формулы значительным образом упрощаются (sin(90°)=1, cos(90°)=0) и состоят, как правило, из двух множителей. Возможен и другой путь решения: свести четвертной треугольник к полярному прямоугольному и производить решение по правилам Модюи-Непера.
Сферические треугольники ABC и A1B1C1 называются полярными, если их стороны и углы связаны следующими соотношениями:
т.е. сумма угла данного треугольника с противоположной стороной полярного ему треугольника равна 180°.

Дано: a =31°15.2′, C = 120°15.4′
1) Выполняем схематический чертёж и помечаем данные и искомые элементы.
2) Подбираем необходимые формулы. (по основным формулам сферической тригонометрии)
A – теорема синусов
B – формула котангенсов;
c – формула косинуса стороны;
1.
2. ctg B sin C = ctg b sin a – cos a cos C
3. cos c = cos a cos b + sin a sin b cos C
3) Преобразовываем формулы, отделяем неизвестные, а так же производим анализ формулы на знаки.
1. sin A = sin a sin C
2. tg B = — cos a tg C
3. tg b = — ctg a sec C
а 90° sin C (+), sec C и tg C ( – )
Так как во всех формулах результат положителен, все искомые величины находятся в первой четверти.
4) Составляем схему вычислений и производим вычисления с использованием таблиц 5-а МТ-75(63) Таблица 3.6. Подробности использования таблиц приведены в пояснениях к таблицам. Что бы не менять наименования функций для аргументов больших 90° при входе в таблицу берём их дополнения до 180°.
| lg | lg | lg | ||||
| a=31°15.2′ C=120°15.4′ | sin sin | 9.71502 9.93640 | cos tg | 9.93191 0.23408 | ctg sec | 0.21687 0.29768 |
| sin A | 9.65142 | tg B | 0.16599 | tg b | 0.51455 | |
| A | 26°37.5′ | B | 55°41.5′ | b | 72°59,8′ | |
| A=26°37.5′ | B=55°41.5′ | b=72°59,8′ |
5) Производим контроль вычислений по теореме синусов. Проверку можно производить как на калькуляторе, так и при помощи таблиц логарифмов[1].
lg sin a = 9.71502 lg sin b = 9.98059 lg sin с =10.00000
lg sin A = 9.65142 lg sin B = 9.91699 lg sin C = 9.93640
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Сферический треугольник
Сферический треугольник ABC расположен на поверхности сферы как показано на рисунках.
Стороны a, b, c (являющиеся дугами больших кругов) измеряются величинами опирающихся на них центральных углов.
A, B, C есть углами, противоположными сторонам a, b, c соответственно.
Площадь сферического треугольника $ABC = (A + B + C — pi)R^2$
где R — радиус сферы.
Отношение между сторонами и углами сферического треугольника
Правило косинусов
cos a = cos b ⋅ cos c + sin b ⋅ sin c ⋅ cos A
cos A = — cos B ⋅ cos C + sin B ⋅ sin C ⋅ cos a
с подобными результатами при использовании других сторон и углов.
с подобными результатами при использовании других сторон и углов.
Подобные утверждения справедливы и для других углов и сторон.
где $S = frac$.
Подобные утверждения справедливы и для других углов и сторон.
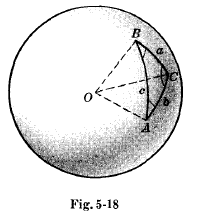
Правила Непера для прямоугольного сферического треугольника
За исключением прямоугольного угла C, есть пять частей сферического треугольника ABC, которые приведены на рис. 5-19 и обозначены как a, b, A, c, B.
Предположим, что эти части расположены по кругу, как на рис. 5-20, где мы допишем префикс co (означающий дополнение) к гипотенузе c и углам A и B.
Любая из этих частей круга называется средняя часть, две другие соседние части называются смежные части и две другие оставшиеся части называются противоположные части.
Синус любой средней части равен произведению тангенсов смежных частей.
Синус любой средней части равен произведению косинусов противоположных частей.
Пример:
Так как co-A = 90° — A, co-B = 90° — B, мы имеем
sin a = tg b ⋅ tg(co-B) или sin a = tg b ⋅ ctg B
sin(co-A) = cos a ⋅ cos(co-B) или cos A = cos a ⋅ sin B.
🔥 Видео
Решение прямоугольных треугольниковСкачать

МОС. ЛР 7.Скачать

9. Площадь сферического треугольникаСкачать

Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

ЗАДАНИЕ 1 ЕГЭ (ПРОФИЛЬ). РЕШЕНИЕ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА.Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

РЕШУ ЕГЭ. Планиметрия (ЕГЭ, задание 6): Решение прямоугольного треугольникаСкачать

Задача — гроб. Меньше 1 людей могут её решитьСкачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Высота, биссектриса, медиана. 7 класс.Скачать

МОРСКАЯ НАВИГАЦИЯ | СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯСкачать

☀️ГЕОМЕТРИЯ В ЕГЭ | ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК | ЗАДАНИЕ 3 ЕГЭ 2022 | СИНУСЫ, КОСИНУСЫ, ТАНГЕНСЫСкачать

9 класс, 15 урок, Решение треугольниковСкачать

Лекция 1. Точка на прямой. Метод прямоугольного треугольникаСкачать

Решение прямоугольных треугольников. Синус, косинус, тангенс, котангенс. Решение задачСкачать