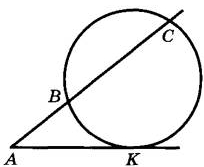
Через точку А, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке К. Другая прямая пересекает окружность в точках В и С, причём АВ = 4, BС = 12. Найдите АК.
Источник: ОГЭ Ященко 2022 (50 вариантов)
Найдём АС:
АС = АВ + ВС = 4 + 12 = 16
По теореме о секущей и касательной (подробно о ней здесь):
Если из одной точки (А) к окружности проведены секущая (АС) и касательная (АК), то произведение всей секущей (АС) на ее внешнюю часть (АВ) равно квадрату отрезка касательной (АК).
АС·АВ = АК 2
16·4 = АК 2
64 = АК 2
АК = √64 = 8
Ответ: 8.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 5
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Видео:Геометрия Докажите, что если через точку A к окружности проведены касательная AM (M – точка касания)Скачать

Через точку А к данной окружности проведены касательная АВ (В — точка касания) и секущая AD, проходящая через центр О
Видео:№635. Через точку А окружности проведены касательная и хорда, равная радиусу окружности.Скачать

Ваш ответ
Видео:Через точку A, лежащую вне окружности, проведены две прямые.Скачать

решение вопроса
Видео:Из точки A проведены две касательные к окружности ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,013
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
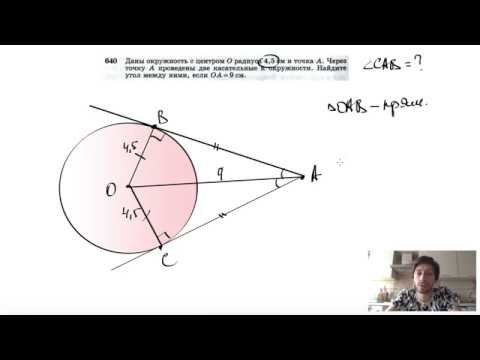
Видео:№640. Даны окружность с центром О радиуса 4,5 см и точка А. Через точку А проведены две касательныеСкачать
Сможете ли вы решить задачу, которую Михаил Мишустин задал школьникам
А вы сможете решить задачу, которую премьер-министр России задал школьникам? С виду она простая, но не обольщайтесь
Задача, которую российский премьер-министр задал школьникам, имела довольно короткую формулировку: проведите из заданной точки на окружности прямую, перпендикулярную ее диаметру, не используя измерительных приборов вроде линейки с делениями. Все, что у вас есть — линейка без делений, при помощи которой можно чертить лишь прямые линии. Наглядно условие задачи можно увидеть на рисунке ниже.
Итак, как же решить такую нетривиальную задачу? Для начала нужно соединить концы диаметра с красной точкой на окружности. Угол между ними получится равным 90°. Показать это очень легко, воспользовавшись теоремой о двух пересекающихся хордах. Согласно ей, угол между двумя хордами равен полусумме дуг, которую охватывает каждая из них. В данном случае, так как хорды проведены из точек диаметра, их сумма составит половину окружности, то есть 180°, а 1/2 этой величины будет равна 90°.
Результаты первого шага можно увидеть на фото статьи, где премьер-министр уже прочертил обе хорды. На втором шаге нужно выбрать еще одну точку на окружности справа от той, с которой мы только что проводили манипуляции. К ней так же проводим две хорды с концов диаметра и получаем второй прямой угол. А теперь продлим левую хорду левого прямоугольного треугольника и правую хорду правого до точки пересечения за пределами окружности, как показано на рисунке ниже.
Проведенная из вершины этого большого треугольника прямая, проходящая через пересечение двух высот, тоже будет высотой исходе из теоремы о точке пересечения высот треугольника. Теперь нам необходимо построить параллельную этой высоте прямую, которая проходит через красную точку. Для этого продлеваем высоту большого треугольника до пересечения с противоположной частью окружности. Затем проводим прямую через точку пересечения высоты с верхней частью окружности и через красную точку. Продлеваем диаметр за пределы окружности до пересечения с полученной до этого прямой.
Ну, и наконец, проводим из получившейся точки пересечения прямую к точке, где встречается высота и нижняя часть окружности. То место, где последняя прямая пересекла окружность, и будет «копией» красной точки, но на нижней полусфере. Соединяем две точки и полученная прямая будет перпендикулярна диаметру. Более наглядно — на рисунке ниже.
🎬 Видео
№672. Через точку А, лежащую вне окружности, проведены две секущие, одна из которых пересекаетСкачать

Геометрия Через точку A, лежащую вне окружности, проведены две прямые, одна из которых касаетсяСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

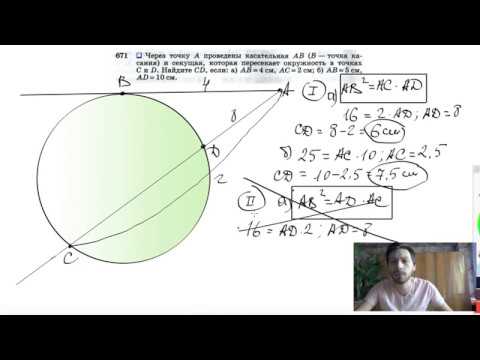
№671. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекаетСкачать
Геометрия Через точку A проведены к окружности касательная AM (M – точка касания) и секущаяСкачать

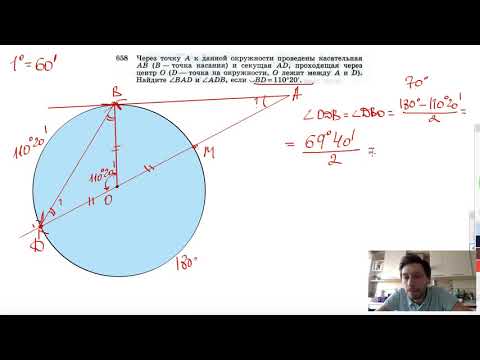
№658. Через точку А к данной окружности проведены касательная АВ (В — точка касания) и секущая ADСкачать
Геометрия Через точку A, лежащую вне окружности, проведены две прямые, одна из которых пересекаетСкачать

ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ в точке ЗАДАЧИ 8 классСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

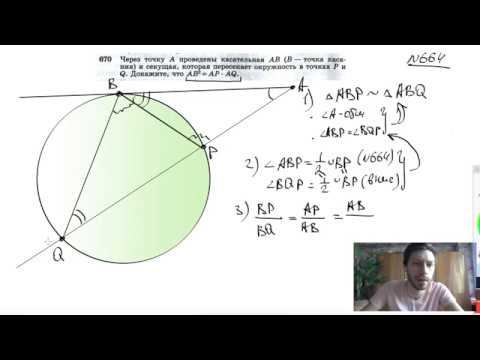
№670. Через точку А проведены касательные АВ (В — точка касания) и секущая, которая пересекаетСкачать
№963. На окружности, заданной уравнением х2+у2 = 25, найдите точки: а) с абсциссой -4Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать