- Исходные данные.
- Развертка прямой призмы.
- Развертка пирамиды.
- Что такое призма: определение, элементы, виды, варианты сечения
- Определение призмы
- Элементы призмы
- Варианты сечения призмы
- Виды призм
- Развертка прямой призмы
- Построение развертки призмы
- Алгоритм построения развертки призмы
- Видео «Развертка призмы»
- 💥 Видео
Видео:Развертка наклонной призмыСкачать

Исходные данные.
Видео:Развертка призмыСкачать

Развертка прямой призмы.
1. Проводим горизонтальную прямую. От произвольной точки G этой прямой откладываем отрезки GU, UЕ, ЕК, КG1, равные длинам сторон основания призмы.
2. Из точек G, G’ восстанавливаем перпендикуляры и на них откладываем величины, равные высоте призмы. Полученные точки соединяем прямой. Прямоугольник GG1’G1’G’ является разверткой боковой поверхности призмы.
3. Для указания на развертке граней призмы из точек U, Е, К восстанавливаем перпендикуляры.
4. Для получения полной развертки поверхности призмы к развертке поверхности пристраиваем многоугольники ее оснований.
5. Для построения на развертке линии пересечения призмы с пирамидой замкнутых ломаных линий 1 2 3 и 4 5 6 7 8 пользуемся вертикальными прямыми. Например, для определения положения точки 1 на развертке поступаем так: на отрезке GU от точки G вправо откладываем отрезок G10, равный отрезку G1.
Из точки 10 восстанавливаем перпендикуляр к отрезку GU и на нем откладываем аппликату z точки 1.
6. Аналогично строим и находим остальные точки.
Видео:Построение призмы высотой 30ммСкачать

Развертка пирамиды.
1. Определяем натуральную величину ребер пирамиды методом вращения. Данные построения выполняются отдельно на кальке.
Аналогичным образом определяется натуральная величина остальных ребер пирамиды.
2. Зная натуральные величины ребер пирамиды, строим ее развертку.
3. На ребрах и на гранях пирамиды (на развертке) определяем вершины пространственной ломаной пересечения пирамиды с призмой.
Видео:Как начертить УСЕЧЕННУЮ ПРИЗМУ В ОБЪЕМЕ и ее РАЗВЕРТКУСкачать

Что такое призма: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения призмы. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Видео:Развертка пирамидыСкачать

Определение призмы
Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.
На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.
Видео:Развёртка призмы и пирамидыСкачать

Элементы призмы
Для рисунка выше:
- Основания – равные многоугольники. Это могут быть треугольники, четырех-, пяти-, шестиугольники и т.д. В нашем случае – это параллелограммы (или прямоугольники) ABCD и A1B1C1D1.
Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:
Примечание: свойства призмы представлены в отдельной публикации.
Видео:Определение натуральной величины сечения прямой призмы с плоскостью . Построение развертки призмы.Скачать

Варианты сечения призмы
- Диагональное сечение – секущая плоскость проходит через диагональ основания призмы и два соответствующих боковых ребра.
Примечание: У треугольной призмы нет диагонального сечения, т.к. основанием фигуры является треугольник, у которого нет диагоналей.
- Перпендикулярное сечение – секущая плоскость пересекает все боковые ребра под прямым углом.
Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем.
Видео:5_Развертка призмы (раскатка)Скачать

Виды призм
Рассмотрим разновидности фигуры с треугольным основанием.
- Прямая призма – боковые грани расположены под прямым углом к основаниям (т.е. перпендикулярны им). Высота такой фигуры равняется ее боковому ребру.
- Наклонная призма – боковые грани фигуры не перпендикулярны ее основаниям.
- Правильная призма – основаниями являются правильные многоугольники. Может быть прямой или наклонной.
- Усеченная призма – часть фигуры, оставшаяся после пересечения ее плоскостью, не параллельной основаниям. Также может быть как прямой, так и наклонной.
Видео:Построение развертки пирамиды и призмыСкачать

Развертка прямой призмы
Дано:
Пересечение пирамиды и призмы
Необходимо:
Построить развертку прямой призмы и показать на ней линию пересечения призмы с пирамидой.
Построение развертки прямой призмы намного легче, чем развертка пирамиды.
Видео:7_Линия сечения на развертке призмыСкачать

Построение развертки призмы
Построение развертки прямой призмы облегчается тем, что все размеры для развертки берутся с эпюр и нам не надо находить натуральные величины ребер призмы. Так как дана прямая призма, то боковые ребра призмы проецируются на фронтальную плоскость проекций в натуральную величину. Ребра оснований прямой призмы параллельны горизонтальной плоскости проекций и проецируются на нее также в натуральную величину.
Видео:№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать

Алгоритм построения развертки призмы
- Проводим горизонтальную прямую.
- От произвольной точки G этой прямой откладываем отрезки GU, UE, ЕК, КG равные длинам сторон основания призмы.
- Из точек G, U, . восстанавливают перпендикуляры и на них откладывают величины равные высоте призмы. Полученные точки соединяют прямой. Прямоугольник GG1G1G является разверткой боковой поверхности призмы. Для указания на развертке граней призмы из точек U, E, K восставляют перпендикуляры.
- Для получения полной развертки поверхности призмы к развертке поверхности пристраивают многоугольники ее оснований.
Для построения на развертке линии пересечения призмы с пирамидой замкнутых ломанных линий 1, 2, 3 и 4, 5, 6, 7, 8 пользуемся вертикальными прямыми.
Более подробно в видеоуроке по начертательной геометрии в Автокад
Видео:Шестиугольная призма.Ортогональные и изометрическая проекции.Урок 17.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Видео «Развертка призмы»
💥 Видео
Лекция №6 Построения разверток многогранниковСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

[Начертательная геометрия] Развертка призмы способ нормального сеченияСкачать
![[Начертательная геометрия] Развертка призмы способ нормального сечения](https://i.ytimg.com/vi/25c8vpG37DA/0.jpg)
Площадь поверхности призмы. 11 класс.Скачать

3_Развертка пирамидыСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

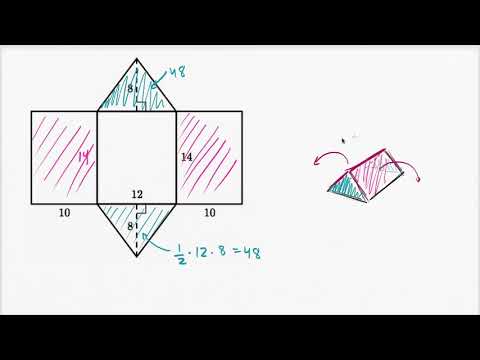
Нахождение площади поверхности треугольной призмы при помощи развёртки (видео 5)| Объём и ПлощадьСкачать
Развертка цилиндраСкачать












 Примечание: У треугольной призмы нет диагонального сечения, т.к. основанием фигуры является треугольник, у которого нет диагоналей.
Примечание: У треугольной призмы нет диагонального сечения, т.к. основанием фигуры является треугольник, у которого нет диагоналей.





