Равнобедренный тупоугольный треугольник свойства

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Равнобедренный треугольник. 7 класс.Скачать

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
4. Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Видео:Геометрия 7 класс (Урок№32 - Повторение. Равнобедренный треугольник и его свойства.)Скачать

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Равнобедренный тупоугольный треугольник – основание, формула

Равнобедренный треугольник наиболее часто встречается в задачах по геометрии. Так сложилось, что равнобедренный треугольник не столь прост в решении, как правильный, но при этом обладает рядом интересных свойств, которые могут затруднить решение задачи.

Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Равнобедренный треугольник

Равнобедренным треугольником зовется треугольник, две стороны которого равны между собой. Тогда третья сторона зовется основанием, а равные стороны считаются боковыми.

Рис. 1. Равнобедренный треугольник.

Любой равнобедренный треугольник имеет ряд свойств:

• Углы при основании равнобедренного треугольника равны.
• Медиана, проведенная к основанию равнобедренного треугольника является биссектрисой и высотой.

Именно эти два свойства определяют специфические особенности равнобедренных треугольников. Как и произвольные треугольник, равнобедренные треугольники бывают 3 видов:

• Остроугольные
• Прямоугольные
• Тупоугольные.

Углы при основании равнобедренного треугольника равны, а сумма углов треугольника всегда равна 180 градусам. Поэтому в равнобедренном и тупоугольном треугольнике наибольший угол всегда лежит напротив основания. Если такой угол лежал бы при основании, то сумма углов превысила бы 180 градусов, а это невозможно.

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Тупоугольный треугольник

Тупой угол это угол больше 90 градусов. Очень часто тупоугольный треугольник стараются изобразить так, чтобы тупой угол находился у основания треугольника. Такой подход облегчает восприятие фигуры.

Рис. 2. Тупоугольный треугольник.

В любой треугольник тупой угол добавляет несколько особенностей:

• Одна из высот треугольника будет проходить вне треугольника. Она упадет на продолжение одной из сторон.
• Ортоцентр, т.е. точка пересечения высот треугольника будет находится за пределами треугольника.
• Два других угла треугольника всегда будут острыми.

Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

Равнобедренный тупоугольный треугольник

Равнобедренный треугольник это треугольник, который с одной стороны содержит в себе тупой угол, с другой имеет две равные между собой стороны.

Такой равнобедренный треугольник сложно воспринимать визуально. Дело в том, что с одной стороны тупоугольные треугольники ученики часто изображают так, чтобы тупой угол был при основании.

Но если тупой угол начертить в основании, то реальное основание тупоугольного равнобедренного треугольника будет визуально совпадать с боковой стороной. Такой подход очень часто приводит к ошибкам. Поэтому равнобедренный тупоугольный треугольник лучше рисовать с тупым углом напротив основания, а сам угол подписывать прямо на чертеже.

Рис. 3. Равнобедренный тупоугольный треугольник.

С другой стороны, этот подход не всегда помогает воспринимать фигуру именно как тупоугольный треугольник. Поэтому и нужно подписывать углы, а при решении доказывать или проверять условие на наличие доказательств существования тупого угла в треугольнике.

Видео:Тупоугольный треугольник для острого умаСкачать

Что мы узнали?

Мы узнали, что такое тупоугольный равнобедренный треугольник и какими особенностями он обладает. Поговорили о том, как лучше начертить тупоугольный треугольник и выделили проблемы, которые могут возникнуть с этим вопросом при решении задач.

Видео:Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

Равнобедренный тупоугольный треугольник

Средняя оценка: 4.8

Всего получено оценок: 199.

Средняя оценка: 4.8

Всего получено оценок: 199.

Равнобедренный треугольник наиболее часто встречается в задачах по геометрии. Так сложилось, что равнобедренный треугольник не столь прост в решении, как правильный, но при этом обладает рядом интересных свойств, которые могут затруднить решение задачи.

Видео:Равнобедренный тупоугольный треугольникСкачать

Равнобедренный треугольник

Равнобедренным треугольником называется треугольник, две стороны которого равны между собой. Тогда третья сторона называется основанием, а равные стороны считаются боковыми.

Рис. 1. Равнобедренный треугольник.

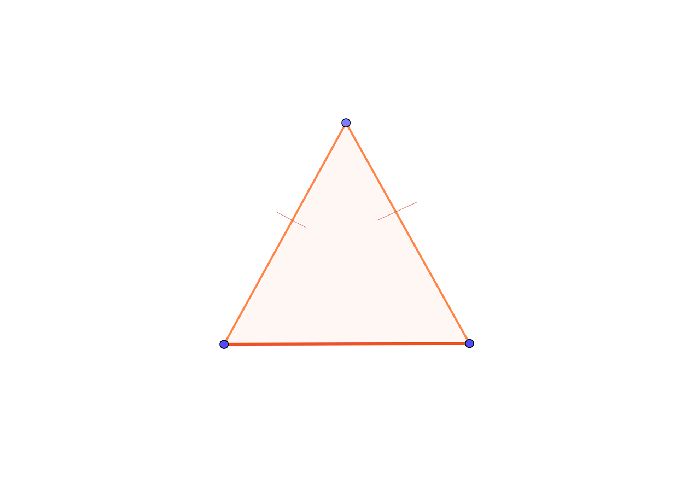
Любой равнобедренный треугольник имеет ряд свойств:

• Углы при основании равнобедренного треугольника равны.
• Медиана, проведенная к основанию равнобедренного треугольника является биссектрисой и высотой.

Именно эти два свойства определяют специфические особенности равнобедренных треугольников. Как и произвольные треугольник, равнобедренные треугольники бывают 3 видов:

• Остроугольные
• Прямоугольные
• Тупоугольные.

Углы при основании равнобедренного треугольника равны, а сумма углов треугольника всегда равна 180 градусам. Поэтому в равнобедренном и тупоугольном треугольнике наибольший угол всегда лежит напротив основания. Если такой угол лежал бы при основании, то сумма углов превысила бы 180 градусов, а это невозможно.

Видео:Геометрия 7 класса в одной задаче. Геометрия 7 класс кратко | МатематикаСкачать

Тупоугольный треугольник

Тупой угол это угол больше 90 градусов. Очень часто тупоугольный треугольник стараются изобразить так, чтобы тупой угол находился у основания треугольника. Такой подход облегчает восприятие фигуры.

Рис. 2. Тупоугольный треугольник.

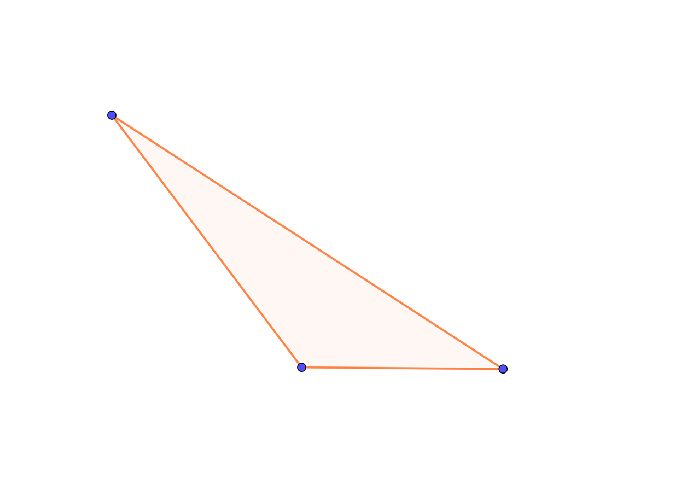
В любой треугольник тупой угол добавляет несколько особенностей:

• Две высоты тупоугольного треугольника будут проходить вне треугольника. Они падают на продолжение одной из сторон.
• Ортоцентр, т.е. точка пересечения высот треугольника будет находится за пределами треугольника.
• Два других угла треугольника всегда будут острыми.

Видео:Можно ли так повернуть налево?/Три задачки для опытных водителейСкачать

Равнобедренный тупоугольный треугольник

Равнобедренный треугольник – это треугольник, который с одной стороны содержит в себе тупой угол, а с другой стороны имеет две равные между собой стороны.

Такой равнобедренный треугольник сложно воспринимать визуально. Дело в том, что с одной стороны тупоугольные треугольники ученики часто изображают так, чтобы тупой угол был при основании.

Но если тупой угол начертить в основании, то реальное основание тупоугольного равнобедренного треугольника будет визуально совпадать с боковой стороной. Такой подход очень часто приводит к ошибкам. Поэтому равнобедренный тупоугольный треугольник лучше рисовать с тупым углом напротив основания, а сам угол подписывать прямо на чертеже.

Рис. 3. Равнобедренный тупоугольный треугольник.

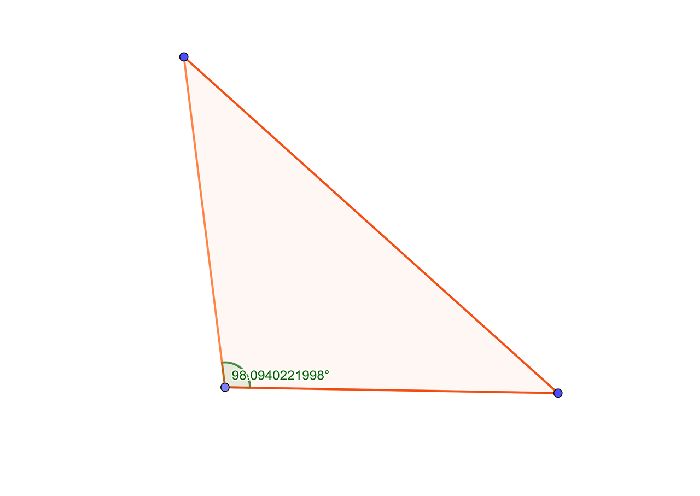
С другой стороны, этот подход не всегда помогает воспринимать фигуру именно как тупоугольный треугольник. Поэтому и нужно подписывать углы, а при решении доказывать или проверять условие на наличие доказательств существования тупого угла в треугольнике.

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Что мы узнали?

Мы узнали, что такое тупоугольный равнобедренный треугольник и какими особенностями он обладает. Поговорили о том, как лучше начертить тупоугольный треугольник и выделили проблемы, которые могут возникнуть с этим вопросом при решении задач.

💥 Видео

Свойства равнобедренного треугольника | Геометрия 7-9 класс #19 | ИнфоурокСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Виды треугольниковСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

32. Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать