Равнобедренный треугольник с углом 120 вписан в окружность

Геометрия | 10 — 11 классы

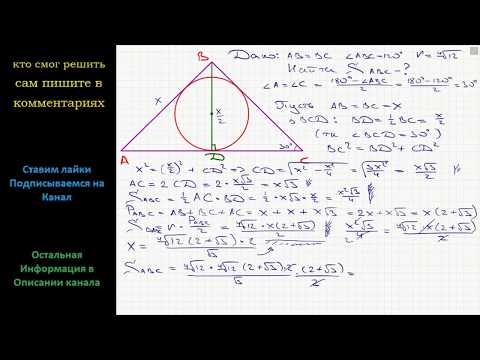
Равнобедренный треугольник вписан в окружность радиуса 4 √ 3 НАЙДИТЕ ВЫСОТУ, ПРОВЕДЁННУЮ К БОКОВОЙ СТОРОНЕ, ЕСЛИ ОДИН ИЗ УГЛОВ ТРЕУГОЛЬНИКА РАВЕН 120 ГРАДУСОВ.

При построение получим треугольник АВС 120 * при вершине .

Соединим А и С с центром окружности О.

Получим 2 треугольника АВО и ВСО равно сторонних по 60 * у каждого угла.

О — центр окружности.

Высота треугольника АВС будет равна высоте треугольника АВО, как равновеликие.

Значит находим высоту .

H = R * cos 60 * = 4 / 3 * / 3 / 2 = 4 * 3 / 2 = 6

Ответ : высота равна 6.

Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

В равнобедренном треугольнике боковая сторона равна 40, а диаметр описанной окружности равен 50?

В равнобедренном треугольнике боковая сторона равна 40, а диаметр описанной окружности равен 50.

Найдите радиус вписанной в данной треугольник окружности.

Видео:Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

Площадь равнобедренного треугольника равна S, угол между высотой, проведенной к боковой стороне, и основанием равен а?

Площадь равнобедренного треугольника равна S, угол между высотой, проведенной к боковой стороне, и основанием равен а.

Найти радиус окружности вписанной в данный треугольник.

Видео:Геометрия В равнобедренный треугольник с углом 120 при вершине и боковой стороной а вписанаСкачать

Основание равнобедренного треугольника = 18см, боковая сторона = 15см, найдите радиусы вписанной в треугольник окружности и описанной около треугольника окружности?

Основание равнобедренного треугольника = 18см, боковая сторона = 15см, найдите радиусы вписанной в треугольник окружности и описанной около треугольника окружности.

Видео:Геометрия Найти площадь равнобедренного треугольника с углом 120, если радиус вписанного круга равенСкачать

1. Высота , проведённая к боковой стороне тупоугольного равнобедренного треугольника , образует с боковой стороны угол 16 градусов?

1. Высота , проведённая к боковой стороне тупоугольного равнобедренного треугольника , образует с боковой стороны угол 16 градусов.

Найдите углы треугольника.

Видео:ЕГЭ Математика Задание 6#27862Скачать

В равнобеддренном треугольнике угол между основанием м высотой, проведённой к боковой стороне, равен 24°?

В равнобеддренном треугольнике угол между основанием м высотой, проведённой к боковой стороне, равен 24°.

Найдите углы равнобедренного треугольника.

Видео:№707. Угол, противолежащий основанию равнобедренного треугольника, равен 120°, боковая сторонаСкачать

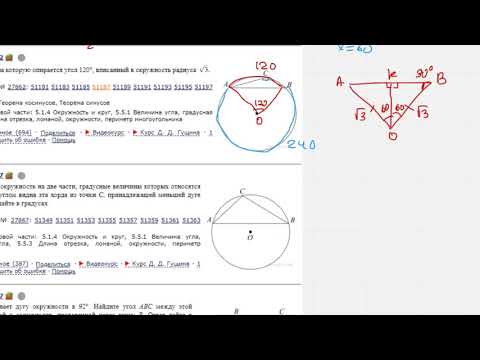
1)Радиус окружности , вписанной в правильный треугольник, равен 29?

1)Радиус окружности , вписанной в правильный треугольник, равен 29.

Найдите высоту этого треугольника.

2)Боковые стороны равнобедренного треугольника равны 60, основание равно 72.

Найдите радиус окружности, описанной около этого треугольника.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведённая к основанию, — 8 см?

В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведённая к основанию, — 8 см.

Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности описанной около этого треугольника.

Видео:Задачи на ОкружностьСкачать

В равнобедренном треугольнике боковая сторона равна 40, а радиус описанной окружности равен 25?

В равнобедренном треугольнике боковая сторона равна 40, а радиус описанной окружности равен 25.

Найдите радиус вписанной окружности в данный треугольник.

Видео:Равнобедренный треугольник с углом 120°Скачать

В равнобедренном треугольнике один из углов равен 120 градусов, а основание 12 см?

В равнобедренном треугольнике один из углов равен 120 градусов, а основание 12 см.

Найдите высоту, проведённую к боковой стороне.

Видео:№250. Основанием пирамиды является равнобедренный треугольник с углом 120°. Боковые ребраСкачать

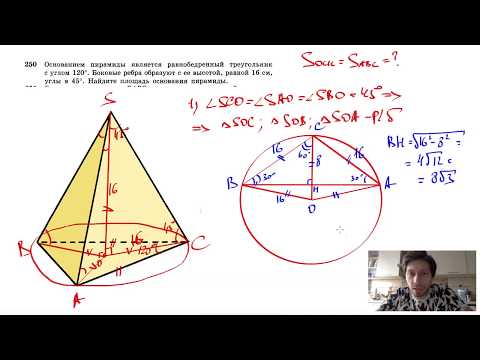
В равнобедренном треугольнике один из углов равен 120 градусов, а основание равно 4 см?

В равнобедренном треугольнике один из углов равен 120 градусов, а основание равно 4 см.

Найдите высоту, проведённую к боковой стороне.

На этой странице вы найдете ответ на вопрос Равнобедренный треугольник вписан в окружность радиуса 4 √ 3 НАЙДИТЕ ВЫСОТУ, ПРОВЕДЁННУЮ К БОКОВОЙ СТОРОНЕ, ЕСЛИ ОДИН ИЗ УГЛОВ ТРЕУГОЛЬНИКА РАВЕН 120 ГРАДУСОВ?. Вопрос соответствует категории Геометрия и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Видео:№259. Угол, противолежащий основанию равнобедренного треугольника, равен 120°. Высота, проведеннаяСкачать

Треугольник вписанный в окружность

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:№703. В окружность вписан равнобедренный треугольник ABC с основанием ВС. Найдите углы треугольникаСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:В равнобедренном треуг один из углов 120 , основание 4см, найдите высоту проведенную к бок сторонеСкачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:ЕГЭ 6 номер. Нахождение диаметра описанной окружности около равнобедренного треугольникаСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Равнобедренный треугольник с углом 120 вписан в окружность

В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на отрезке BC, а вершина E — на отрезке AB.

а) Докажите, что FH = 2DH.

б) Найдите площадь прямоугольника DEFH, если AB = 4.

а) Пусть P — основание перпендикуляра, опущенного из точки D на прямую AB, тогда DH = DP.

В равнобедренном треугольнике EAD угол AED равен 30°. В прямоугольном треугольнике EPD находим откуда получаем, что FH = 2DH.

б) Пусть AM — высота треугольника ABC — пересекает ED в точке N. Тогда

Пусть DH = EF = x, тогда FH = ED = 2x. Треугольники ABC и AED подобны, следовательно,

Значит, площадь прямоугольника DEFH равна

Ответ:

Приведем решение пункта а) Сергея Федорова.

Треугольник ABC равнобедренный, следовательно,

Углы BDE и DBC равны как накрест лежащие, угол DBC равен углу DBE, поскольку BD является биссектрисой, следовательно, углы BDE и DBE равны, тогда треугольник DBE равнобедренный, DE = BE.

В треугольнике BFE катет EF лежит против угла в 30 градусов, следовательно, BE = 2EF, тогда DE = 2EF.

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, 💥 Видео Свойство окружности, описанной около равнобедренного треугольникаСкачать Вписанные углы в окружностиСкачать 7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности