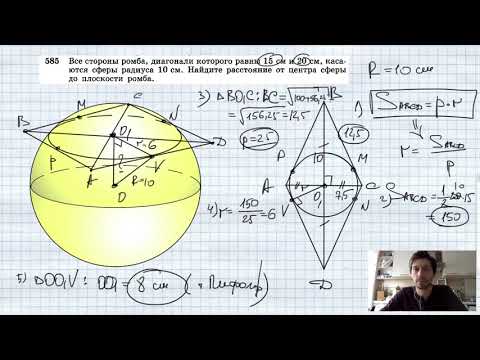
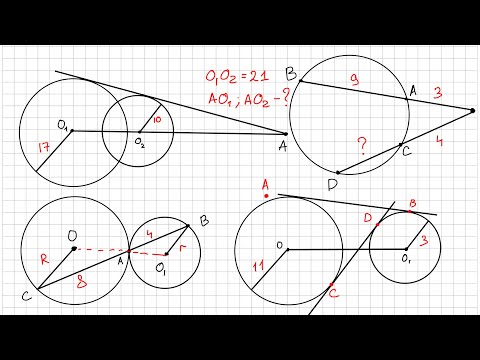
Расстояние между центрами окружностей радиусов 2 и 8 равно 15. Этих окружностей и их общей внутренней касательной касается третья окружность. Найдите её радиус.
Пусть a — расстояние между центрами окружностей радиусов r и R, a ≥ r + R. Если общая внутренняя касательная касается окружностей в точках C и D, то
Действительно, пусть O1 и O2 — центры окружностей радиусов r и R соответственно (см. рис.). Из точки O2 опустим перпендикуляр O2F на прямую O1C. Из прямоугольного треугольника O1FO2 находим, что
Пусть x — радиус искомой окружности, O3 — её центр. Заметим, что прямая CD — либо общая внешняя касательная окружностей с центрами O3 и O2 (см. рис.), либо общая внешняя касательная окружностей с центрами O3 и O1 (см. рис.). В первом них этих случаев искомая окружность касается прямой CD в точке C, во втором — в точке D.
По доказанному 
В первом случае CD — общая внешняя касательная к окружности с центрами O3 и O2, поэтому 
значит, 
откуда 
Во втором случае CD — общая внешняя касательная к окружностям с центрами O3 и O1, поэтому 
откуда 
Ответ: 
или 
- Как расположены относительно друг друга две окружности, если расстояние между их центрами равно : а)15 см, а радиусы равны 9 см и 7см ; б) 8 см, а диаметры равны 20 см и 2 см?
- Привет, помогите пожалуйста, я буду очень благодарна за решение задач?
- Две окружности касаются внешним образом?
- 1. Две окружности, радиусы которых равны r, проходят через центры друг друга?
- Как расположены относительно друг друга две окружности, если расстояние между их центрами равно : а) 15 см, а радиусы равны 9 см и 7 см ; б) 8 см, а диаметры равны 20 см и 2 см?
- Две окружности касаются внешним образом?
- 1 номер?
- Две окружности диаметром 10 см и 15 см касаются друг друга внутренним образом ?
- Две окружности с радиусами 3 см и 6 см касаются друг друга внешним образом чему равно расстояние Между центрами окружностей?
- ДВЕ ОКРУЖНОСТИ НЕ ПЕРЕСЕКАЮТСЯ И РАСПОЛОЖЕНЫ ОДНА ВНУТРИ ДРУГОЙ?
- Как расположена прямая относительно окружности, если диаметр окружности равен 16 см , а расстояние прямой от центра равно 1) 7 см ; 2) 8 см ; 3) 9 см?
- Как найти расстояние между центрами окружностей
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Ответ
- Проверено экспертом
Как расположены относительно друг друга две окружности, если расстояние между их центрами равно : а)15 см, а радиусы равны 9 см и 7см ; б) 8 см, а диаметры равны 20 см и 2 см?
Геометрия | 10 — 11 классы
Как расположены относительно друг друга две окружности, если расстояние между их центрами равно : а)15 см, а радиусы равны 9 см и 7см ; б) 8 см, а диаметры равны 20 см и 2 см?
А) они пересекутся, т.
К. расстояние между ними 15, а радиусы в сумме дают 16
б)тоже пересекаться, т.
8 , а радиусы в сумме дают 11.
Привет, помогите пожалуйста, я буду очень благодарна за решение задач?
Привет, помогите пожалуйста, я буду очень благодарна за решение задач.
Спасибо * 1)Запишите условие того, что прямая и окружность радиуса 5см : а)не имеют ни одной общей точки.
2)Как расположены относительно друг друга две окружности, если расстояние между их центрами равно : а)15см, а радиусы равны 9см и 7см.
Б)8см, а диаметры равны 20см и 2 см.
3)Две окуржности касаются внутренним образом.
Радиус одной окружности в три раза больше радиуса другой.
Найдите диаметры окружностей, если расстояние между их центрами равно 6см.
Помогите всё это решить!
Буду очень благодарна!
Две окружности касаются внешним образом?
Две окружности касаются внешним образом.
Радиус одной окружности на 3 см меньше радиуса другой окружности.
Найдите диаметры окружностей, если расстояние между их центрами равно 11 см.
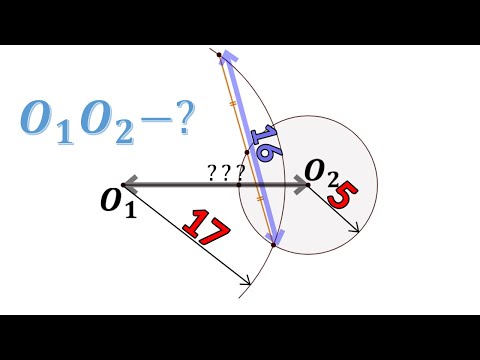
1. Две окружности, радиусы которых равны r, проходят через центры друг друга?
1. Две окружности, радиусы которых равны r, проходят через центры друг друга.
Выразите r через их общую хорду.
2. Две равные и взаимно перпендикулярные хорды окружности в точке пересечения делятся на части длиной 10 см и 16 см.
Найдите радиус окружности.
Как расположены относительно друг друга две окружности, если расстояние между их центрами равно : а) 15 см, а радиусы равны 9 см и 7 см ; б) 8 см, а диаметры равны 20 см и 2 см?
Как расположены относительно друг друга две окружности, если расстояние между их центрами равно : а) 15 см, а радиусы равны 9 см и 7 см ; б) 8 см, а диаметры равны 20 см и 2 см?
Подробное решение, пожалуйста.
Две окружности касаются внешним образом?
Две окружности касаются внешним образом.
Радиус одной окружности на 3 см меньше радиуса другой окружности.
Найдите диаметры окружностей, если расстояние между их центрами равно 11 см.
1 номер?
Радиус окружности 2, 5 см.
Найдите ее диаметр.
Может ли ее хорда быть равной 6 см?
Могут ли касаться две окружности, если их радиусы равны 25 см и 50 см, а расстояние между центрами 60 см?
(решите пожалуйста понятно, и сделайте чертеж).
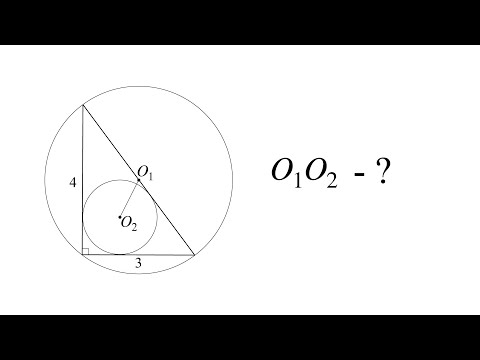
Две окружности диаметром 10 см и 15 см касаются друг друга внутренним образом ?
Две окружности диаметром 10 см и 15 см касаются друг друга внутренним образом .
Найдите расстояние между центрами этих окружностей .
Две окружности с радиусами 3 см и 6 см касаются друг друга внешним образом чему равно расстояние Между центрами окружностей?
Две окружности с радиусами 3 см и 6 см касаются друг друга внешним образом чему равно расстояние Между центрами окружностей.
ДВЕ ОКРУЖНОСТИ НЕ ПЕРЕСЕКАЮТСЯ И РАСПОЛОЖЕНЫ ОДНА ВНУТРИ ДРУГОЙ?
ДВЕ ОКРУЖНОСТИ НЕ ПЕРЕСЕКАЮТСЯ И РАСПОЛОЖЕНЫ ОДНА ВНУТРИ ДРУГОЙ.
ИХ ДИАМЕТРЫ ОТНОСЯТСЯ КАК 2 : 5.
ДИАМЕТР БОЛЬШЕЙ ОКРУЖНОСТИ ДЕЛИТСЯ МЕНЬШЕЙ ОКРУЖНОСТЬЮ НА ТРИ ЧАСТИ, ПРИЧЕМ КРАЙНИЕ РАВНЫ 10 СМ И 5 СМ.
НАЙДИТЕ ДИАМЕТРЫ ОКРУЖНОСТЕЙ И РАССТОЯНИЕ МЕЖДУ ИХ ЦЕНТРАМИ.
Как расположена прямая относительно окружности, если диаметр окружности равен 16 см , а расстояние прямой от центра равно 1) 7 см ; 2) 8 см ; 3) 9 см?
Как расположена прямая относительно окружности, если диаметр окружности равен 16 см , а расстояние прямой от центра равно 1) 7 см ; 2) 8 см ; 3) 9 см?
Вы перешли к вопросу Как расположены относительно друг друга две окружности, если расстояние между их центрами равно : а)15 см, а радиусы равны 9 см и 7см ; б) 8 см, а диаметры равны 20 см и 2 см?. Он относится к категории Геометрия, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.
Всего 5, если учитывать прямую, которая уже есть, если не учитывать то 4.
A(вектор) = = DA₁(вектор) + BC(вектор) + BA(вектор) = = CB₁(вектор) + B₁C₁(вектор) + C₁D₁(вектор) = CD₁(вектор) можно (и нужно) заменить данные векторы равными им. DA₁(вектор) = CB₁(вектор) и т. Д. .
Если один угол — прямой, то угол параллельный ему будет также прямым, а так как сумма любого четырехугольника = 360 градусов, два остальных угла будут равняться 180 градусам, а в ромбе параллельные углы равны каждый будет по 90 градусов, в итоге полу..
В основании правильной треугольной пирамиды лежит правильный (равносторонний) треугольник со стороной (a), а боковые грани пирамиды — равные равнобедренные треугольники. Площадь боковой поверхности пирамиды (Sбок)равна сумме площадей боковых граней ..
1миля(географическая) = 1 / 15 градуса земного экватора ≈ 7, 42км 1верста(путевая, или пятисотная) = 500 саженей ≈ 1066, 8м 1аршин(шаг) = 4 четверти = 28 дюймов = 16 вершков ≈ 71, 12см.
Посмотри внизу таблицу, по твоему вопросу не понятно, что надо.
Углы при меньшем основании : 35, 35. Углы при большем основании : 145, 145.
Нужно взять транспортир. И.
AD = AK + KD = 5 + 15 = 20 Д. П. CH (перпендкуляр AD) BC = KH AK = HD = 5 BC = KH = AD — AK — HD = 20 — 5 — 5 = 10 Ответ AD = 20 ; BC = 10.
Как найти расстояние между центрами окружностей
У Вас недостаточно прав для добавления комментариев.
Вам необходимо зарегистрироваться на сайте
Все права защищены 2019
Перепечатка информации возможна только при наличии
согласия администратора и активной ссылки на источник!
 Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Расстояние между центрами окружностей больше суммы их радиусов
Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Расстояние между центрами окружностей больше суммы их радиусов
Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей
Расстояние между центрами окружностей больше суммы их радиусов
Расстояние между центрами окружностей равно сумме их радиусов
Расстояние между центрами окружностей равно разности их радиусов
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
Расстояние между центрами окружностей меньше разности их радиусов
d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.
Каждая из окружностей лежит вне другой
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
| Внешняя касательная к двум окружностям | |
 | |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.
Существует единственная общая внешняя касательная. Других общих касательных нет.
Существуют две общих внешних касательных. Других общих касательных нет.
Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Внутреннее касание двух окружностей |
| Окружности пересекаются в двух точках |
| Внешнее касание двух окружностей |
| Каждая из окружностей лежит вне другой |
| Фигура | Рисунок | Формула | ||
| Внешняя касательная к двум окружностям |  | |||
| Внутренняя касательная к двум окружностям |  | |||
| Общая хорда двух пересекающихся окружностей |  | |||
| Внешняя касательная к двум окружностям | |
| |
Длина общей внешней касательной к двум окружностям вычисляется по формуле
Длина общей внутренней касательной к двум окружностям вычисляется по формуле
Длина общей хорды двух окружностей вычисляется по формуле
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
Длина общей хорды двух окружностей вычисляется по формуле
Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, ОтветПроверено экспертомУравнение окружности с центром (a;b) и радиусом R центр окружности (-2;6) радиус 6 центр окружности (4;-5)радиус 5 по формуле расстояние между двумя точками : находим расстояние между центрами заданных окружностей |
