Общие касательные к двум окружностям
 Взаимное расположение двух окружностей |
| Общие касательные к двум окружностям |
| Формулы для длин общих касательных и общей хорды |
| Доказательства формул для длин общих касательных и общей хорды |
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Касание окружностей
- Внутреннее касание
- Внешнее касание
- Расстояние между центрами окружностей касающихся внутренним образом
- Как написать хороший ответ?
- 🌟 Видео
Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
| ||
| Внешнее касание двух окружностей | ||
| ||
| Внутреннее касание двух окружностей | ||
| ||
| Окружности пересекаются в двух точках | ||
| ||
| ||
| Каждая из окружностей лежит вне другой | ||
Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
| |
| Внутреннее касание двух окружностей | |
| |
| Окружности пересекаются в двух точках | |
| |
| Внешнее касание двух окружностей | |
| |
| |
| Каждая из окружностей лежит вне другой | |
| |
| Внешняя касательная к двум окружностям | |||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||
| Внутреннее касание двух окружностей | |||||||||||||||||||||
| Окружности пересекаются в двух точках | |||||||||||||||||||||
| Внешнее касание двух окружностей | |||||||||||||||||||||
| Каждая из окружностей лежит вне другой | |||||||||||||||||||||
| Фигура | Рисунок | Формула | ||||||||||||
| Внешняя касательная к двум окружностям |  | |||||||||||||
| Внутренняя касательная к двум окружностям |  | |||||||||||||
| Общая хорда двух пересекающихся окружностей |  | |||||||||||||
| Внешняя касательная к двум окружностям | ||||
| ||||
| Внутренняя касательная к двум окружностям | ||||
| ||||
| Общая хорда двух пересекающихся окружностей | ||||
| ||||
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
Длина общей хорды двух окружностей вычисляется по формуле
Видео:Как найти расстояние между центрами | Олимпиадная математикаСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:расстояние между центрамиСкачать  Касание окружностейГоворят, что две окружности касаются, если они имеют единственную общую точку. Эта точка называется точкой касания окружностей. Касание окружностей бывает внутренним и внешним. Видео:ЕГЭ и ОГЭ. Окружности и касательные, секущие, подобие. Свойства. Расстояние между центрами.Скачать 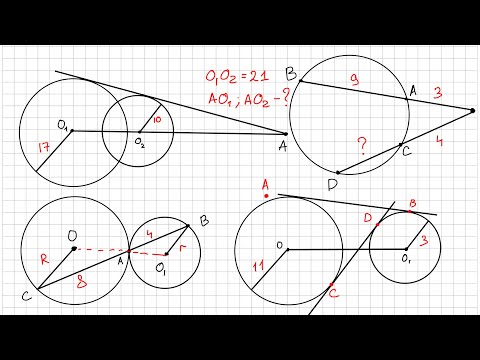 Внутреннее касаниеКасание называется внутренним, если центры окружностей лежат по одну сторону от точки касания окружностей. Построим две окружности, первая с центром A и радиусом AC, отметим на радиусе AC точку B, это будет центр второй окружности с радиусом BC:
Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внутренним образом. При внутреннем касании двух окружностей, расстояние между их центрами равно разности их радиусов. Видео:Урок 47. Взаимное расположение окружностей (8 класс)Скачать  Внешнее касаниеКасание называется внешним, если центры окружностей лежат по разные стороны от точки касания. Построим две окружности, первая с центром A и радиусом AC, вторая с центром B и радиусом BC:
Построенные окружности имеют только одну общую точку C. Говорят, что они касаются внешним образом. При внешнем касании двух окружностей, расстояние между их центрами равно сумме их радиусов. Видео:Окружности касаются внутренним образом.мой вариант решения задачи.#hard.Скачать 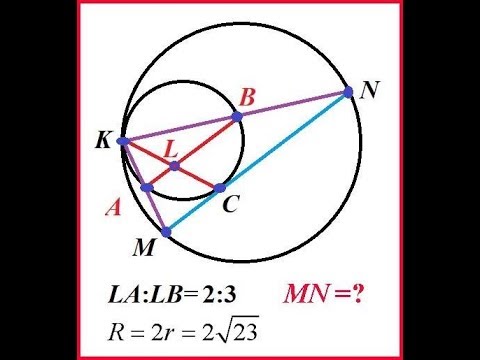 Расстояние между центрами окружностей касающихся внутренним образомВопрос по геометрии: Расстояние между центрами двух окружностей, касающихся внутренним образом, равно 18 см. Найдите радиусы окружностей, если один из них в 4 раза меньше другого. Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ? Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно! Ответы и объяснения 1Примем меньший радиус равнымr, тогда больший = 4r Расстояние между центром меньшей окружности и точкой касания равно r, а между центром большей окружности и точкой касания 4r. Расстояние между центрами окружностей
Знаете ответ? Поделитесь им!Как написать хороший ответ?Чтобы добавить хороший ответ необходимо:
Этого делать не стоит:
Есть сомнения?Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия. Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы! Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения. 🌟 ВидеоКасание окружностейСкачать  Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать  Параметр. Серия 13. Решение задач с окружностями. Касание двух окружностейСкачать  Занятие 1 к главе 9Скачать 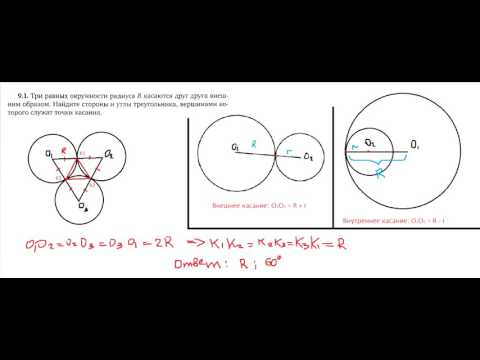 ЕГЭ Задание 16 Комбинация трёх окружностейСкачать  Планиметрия 18 | mathus.ru| окружностей и их общей внутренней касательной касается третья окружностьСкачать  Геометрия. Задача. Окружности.Скачать  Касающиеся окружности.Скачать  Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать  Касание окружностей | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать  ЕГЭ Задание 16 Внутреннее касание двух окружностейСкачать 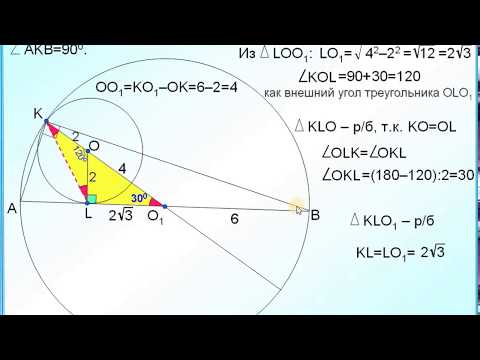 КАСАЮЩИЕСЯ ОКРУЖНОСТИСкачать  ОГЭ Задание 26 Внешнее касание двух окружностейСкачать  |
