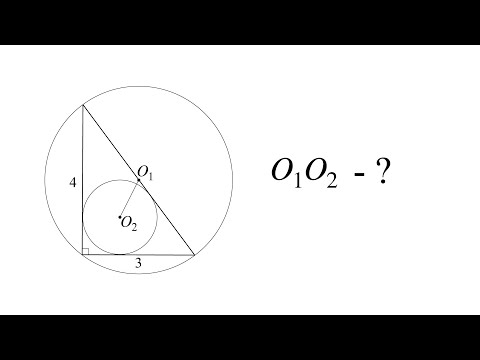Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
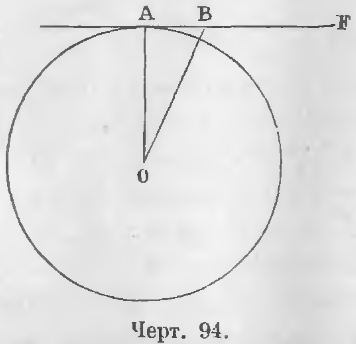
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
- Как найти расстояние между центрами окружностей
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Ответ
- Проверено экспертом
- Математика
- Зависимость между углами, дугами и хордами
- Взаимное отношение хорд и их расстояний от центров
- Относительное положение двух окружностей
- Расстояние между центрами окружностей
- 📺 Видео
Видео:Расстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать

Как найти расстояние между центрами окружностей
У Вас недостаточно прав для добавления комментариев.
Вам необходимо зарегистрироваться на сайте
Все права защищены 2019
Перепечатка информации возможна только при наличии
согласия администратора и активной ссылки на источник!
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
Видео:Планиметрия 12 | mathus.ru | расстояние между центрами пересекающихся окружностейСкачать

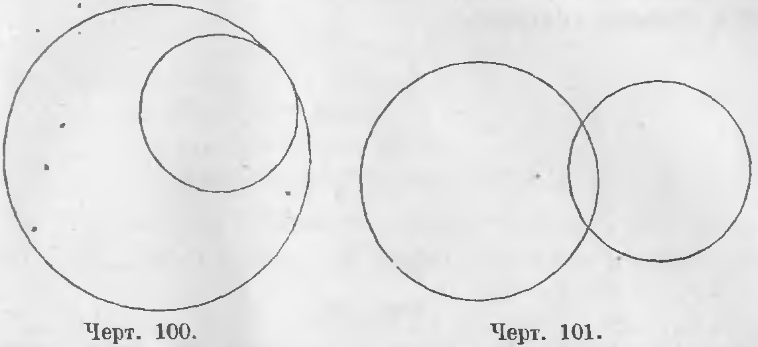
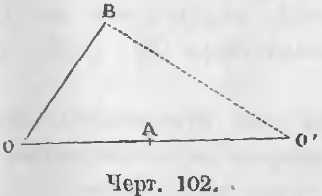
Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  |
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

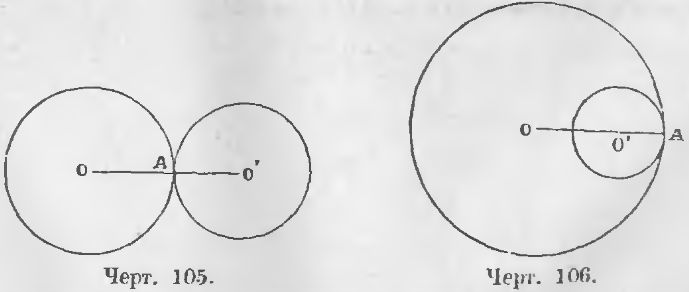
Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов

Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов

Расстояние между центрами окружностей меньше разности их радиусов
d r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей

Расстояние между центрами окружностей больше суммы их радиусов

Расстояние между центрами окружностей равно сумме их радиусов
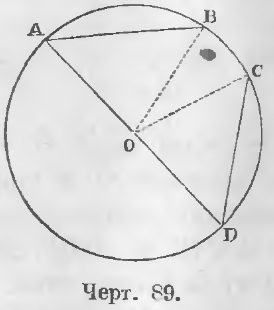
Расстояние между центрами окружностей равно разности их радиусов

Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов
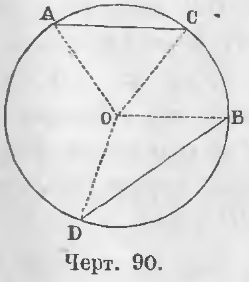
Расстояние между центрами окружностей меньше разности их радиусов
d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

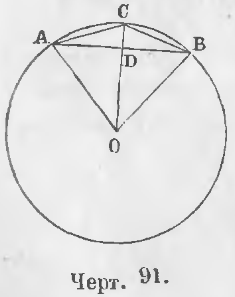
Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

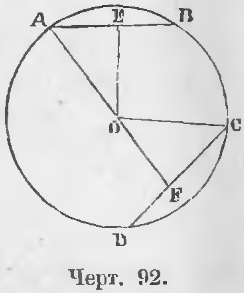
Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также
две общих внешних касательных. Других общих касательных нет.

Каждая из окружностей лежит вне другой
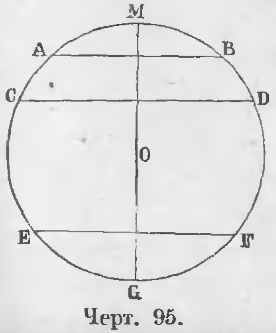
Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

| Внешняя касательная к двум окружностям | |
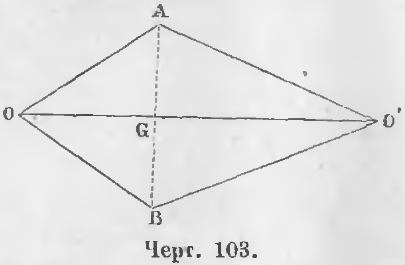
 | |
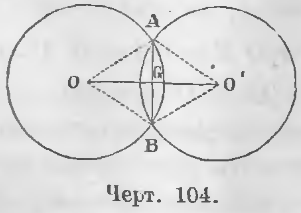
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Внутреннее касание двух окружностей |
| Окружности пересекаются в двух точках |
| Внешнее касание двух окружностей |
| Каждая из окружностей лежит вне другой |
| Фигура | Рисунок | Формула | ||
| Внешняя касательная к двум окружностям |  | |||
| Внутренняя касательная к двум окружностям |  | |||
| Общая хорда двух пересекающихся окружностей |  | |||
| Внешняя касательная к двум окружностям | |
 | |
Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
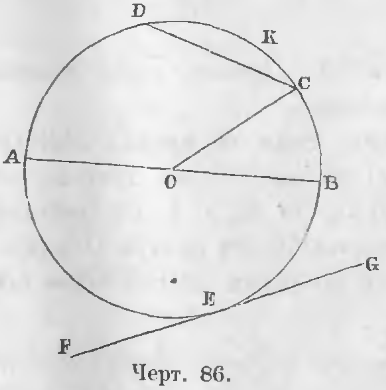
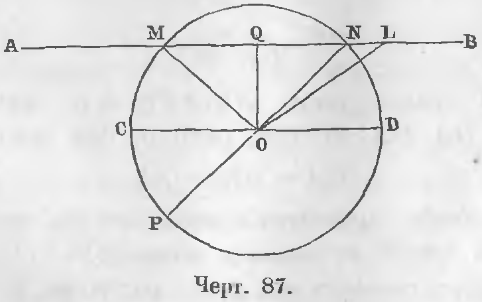
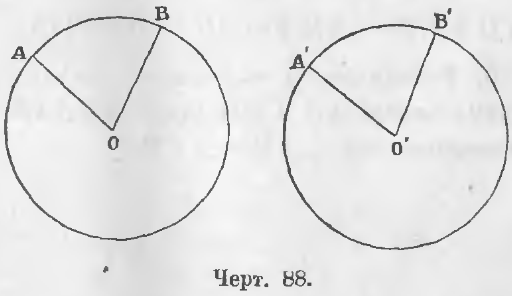
 Длина общей хорды двух окружностей вычисляется по формуле Видео:"Парадоксальное" среднее расстояние между точками на окружностиСкачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:М1152. Расстояние между центрами вписанной и описанной окружностейСкачать 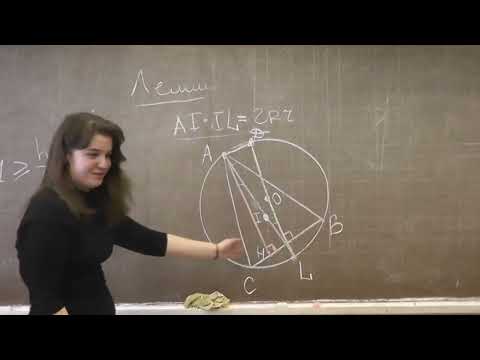 ОтветПроверено экспертомУравнение окружности с центром (a;b) и радиусом R центр окружности (-2;6) радиус 6 центр окружности (4;-5)радиус 5 по формуле расстояние между двумя точками : находим расстояние между центрами заданных окружностей Видео:Планиметрия 5 | mathus.ru | расстояние между центрами окружностей в параллелограммеСкачать  МатематикаОкружность есть такая плоская кривая, у которой все точки находятся на равном расстоянии от одной точки, лежащей внутри ее и называемой центром. Круг. Кругом называется часть плоскости, ограниченная окружностью. Радиус. Радиусом называется отрезок, соединяющий центр с какой-нибудь точкой окружности. Радиус есть расстояние точки окружности от центра. Из самого определения окружности следует, что все ее радиусы равны. На чертеже 86 кривая линия BCDAEB есть окружность, O ее центр, отрезки OA, OB, OC — радиусы. Эти отрезки равны Диаметр. Отрезок, проходящий через центр от одной точки окружности до другой, называется диаметром. Всякий диаметр состоит из двух радиусов, а так как все радиусы равны, то следовательно и все диаметры равны. Дуга есть часть окружности. Слово дуга иногда обозначают знаком ◡, так что дугу BC изображают письменно: ◡BC. Хорда. Отрезок, соединяющий две какие-нибудь точки окружности, называется хордой. Хорда есть прямая, стягивающая две точки дуги. На чертеже 86 линия AB есть диаметр, часть окружности BC есть дуга, прямая CD есть хорда. Сегмент есть часть плоскости, содержащийся между дугой и хордой. Сектор есть часть плоскости, содержащийся между двумя радиусами и дугой круга. На чертеже 86 площадь COB есть сектор, а CKD сегмент. Касательная есть прямая, имеющая с окружностью только одну общую точку, которая называется точкой касания. Углом при центре называется угол, имеющий вершину в центре. На чертеже 86 прямая FG есть касательная, а E точка касания. Теорема 55. Прямая может пересечь окружность только в двух точках. Доказательство. Если бы прямая AB кроме двух точек M и N (черт. 87) имела бы еще третью точку пересечения L, то три точки окружности M, N, L, по свойству окружности, были бы на равном расстоянии от центра O, следовательно, три отрезка MO, NO, LO были бы равны: MO = NO = LO. Если же NO = LO, то вышло бы, что равные наклонные находятся на неравных расстояниях от перпендикуляра OQ, что противоречит свойству косвенных, следовательно, третьей точки пересечения быть не может (ЧТД). Теорема 56. Диаметр делит окружность и круг на две равные части. Доказательство. Перегнем верхнюю часть круга около диаметра CD (черт. 87) до совпадения ее с нижней частью, тогда все точки верхней совпадут с точками нижней части окружности, ибо в противном случае не все точки окружности находились бы на равном расстоянии от центра. Видео:1 2 4 сопряжение окружностейСкачать  Зависимость между углами, дугами и хордамиТеорема 57. В двух равных кругах равным углам при центре соответствуют равные дуги. Дано. Две окружности описаны (черт. 88) одними и теми же радиусами и углы при центре равны: Требуется доказать, что ◡AB = ◡A’B’. Доказательство. Наложим круг O’ на круг O так, чтобы центр O’ совпал с центром O и сторона OA со стороною O’A’. Точка A’ по равенству радиусов совпадает с точкой A. По равенству углов A’O’B’ и AOB отрезок O’B’ пойдет по отрезку OB и по равенству радиусов точка B’ упадет в точку B. Две крайние точки дуги A’B’ совпадут с двумя крайними точками дуги AB, следовательно, и все промежуточные точки дуги A’B’ совпадут с промежуточными точками дуги AB, так как окружность O’ совпадает с окружностью O, ибо они описаны равными радиусами. Теорема 58 (обратная 57). Равным дугам соответствуют равные углы. Дано. Дуги AB и A’B’ равны (◡AB = ◡A’B’) (черт. 88). Требуется доказать, что ∠AOB = ∠A’O’B’. Доказательство. Наложим сектор A’O’B’ на сектор AOB так, чтобы отрезок O’A’ совпал с отрезком OA. Дуга A’B’ упадет на дугу AB и B’ упадет в B. Отрезок B’O’ совпадет с отрезком BO и угол AOB совпадет с углом A’O’B’, следовательно, Теорема 59. Диаметр больше всякой хорды. Даны диаметр CD и хорда MN (черт. 87). Требуется доказать, что CD > MN. Доказательство. Проведем радиусы MO и NO. Ломаная линия MON больше прямой MN MON > MN или MO + ON > MN Так как MO = CO, NO = OD, то заменяя MO и NO равными им величинами, получим неравенства: CO + OD > MN или CD > MN (ЧТД). Теорема 60. Равные хорды стягивают равные дуги. Даны равные хорды AB и CD (черт. 89) (AB = CD). Требуется доказать, что ◡AB = ◡CD. Доказательство. Соединив точки A, B, C, D с центром, имеем OA = OC и OB = OD как радиусы, AB = CD по условию. Следовательно, ∠AOB = ∠COD, откуда ◡AB = ◡CD (ЧТД). Теорема 61 (обратная 60). Равные дуги стягиваются равными хордами. Дано. Дуги AB и CD равны (черт. 89) (◡AB = ◡CD). Требуется доказать, что AB = CD. Доказательство. Два треугольника AOB и COD равны, ибо OA = OC и OB = OD как радиусы, ∠AOB = ∠COD ибо по условию дуги AB и CD равны, а потому и углы равны (теорема 58). Следовательно, AB = CD (ЧТД). Теорема 62. Если дуги меньше полуокружности, то против большей дуги лежит большая хорда. Дано. Дуга BD больше дуги AC (черт. 90) (◡BD > ◡AC). Требуется доказать, что BD > AC. Доказательство. Соединим точки A, C, B, D с центром O. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BOD > AOC. Следовательно, BD > AC (теорема 23) (ЧТД). Теорема 63 (обратная 62). Против большей хорды лежит большая дуга. Дано. Хорда BD больше хорды AC (черт. 90) (BD > AC). Требуется доказать, что ◡BD > ◡AC. Доказательство. В двух треугольниках AOC и BOD OA = OB и OC = OD как радиусы, BD > AC по условию. Поэтому ∠BOD > ∠AOC (теорема 24). Следовательно, ◡BD > ◡AC (ЧТД). Видео:Планиметрия 11 |mathus.ru| расстояние между центрами пересекающихся окружностейСкачать  Взаимное отношение хорд и их расстояний от центровТеорема 64. Радиус, перпендикулярный к хорде, делит как хорду так и дугу пополам. Радиус OC перпендикулярен к хорде AB (черт. 91). Требуется доказать, что AD = BD и ◡AC = ◡CB. Доказательство. Соединим точки A и B с центром O. Равные наклонны OA и OB находятся на равных расстояниях от перпендикуляра OC, следовательно, AD = DB. Если же перпендикуляр CD восставлен из середины отрезка AB, то его точка C находится на равном расстоянии от концов перпендикуляра, поэтому хорды AC и CB равны, а следовательно, т. е. дуга AB делится перпендикуляром OC пополам (ЧТД). Следствие. Перпендикуляр, восставленный из середины хорды, проходит через центр. Доказательство. Так как центр находится на равном расстоянии от концов хорды, то он находится на перпендикуляре, восставленном из середины хорды. Теорема 65. Равные хорды находятся на равном расстоянии от центра. Дано. Хорды AB и CD равны: AB = CD (черт. 92). Требуется доказать, что их расстояния от центра равны, т. е. Доказательство. Соединив точки A и C с центром O, имеем два равных прямоугольных треугольника AEO и COF, ибо OA = OC как радиусы, AE = CF как половины равных хорд (теорема 64). Следовательно, Теорема 66 (обратная 65). На равных расстояниях от центра находятся равные хорды. Дано. Расстояния хорд AB и CD от центра равны, т. е. Требуется доказать, что AB = CD. Доказательство. Два прямоугольных треугольника AEO и COF равны, ибо имеют по равной гипотенузе и равному катету. Действительно, OE = OF по условию, OA = OC как радиусы, следовательно, AE = CF или ½AB = ½CD, откуда Теорема 67. Большая хорда к центру ближе меньшей. Дано. Хорда AB больше хорды AC (черт. 93), т. е. AB > AC. Требуется доказать, что OD ⊥ AO. Требуется доказать, что AF касательная к окружности. Доказательство. Всякая другая точка B перпендикуляра AB находится на расстоянии BO большем AO, ибо наклонная больше перпендикуляра, следовательно точка B находится вне окружности. Таким образом прямая AB имеет с окружностью только одну общую точку A, следовательно, она будет касательной (ЧТД). Теорема 69 (обратная 68). Касательная к окружности, проведенная в конец радиуса, перпендикулярна к радиусу. Дано. Прямая AF касается окружности в точке A (черт. 94). Требуется доказать, что AF ⊥ OA. Доказательство. Прямая AB как касательная имеет с окружностью только одну общую точку A. Всякая другая точка B лежит вне окружности, следовательно, всякий отрезок OB больше OA. Таким образом, отрезок OA есть кратчайшее расстояние точки O от AB, следовательно, OA ⊥ AB (ЧТД). Теорема 70. Между параллельными хордами находятся равные дуги. Дано. Хорды AB и CD параллельны: AB || CD (черт. 95). Требуется доказать, что ◡AC = ◡BD. Доказательство. a) Из центра окружности O опустим перпендикуляр OM на хорду AB, тогла отрезок OM перпендикулярен и к хорде CD. Вычитая второе равенство из первого, получим: ◡CM — ◡AM = ◡MD — ◡MB или b) Если параллельные хорды AB и EF (черт. 95) лежат по обе стороны центра, то, продолжив прямую OM до пересечения с окружностью в точке G, имеем: Так как полуокружности MAG и MBG равны MAG = MBG, то следовательно, Видео:Сможешь найти расстояние между центрами пересекающихся окружностей?Скачать 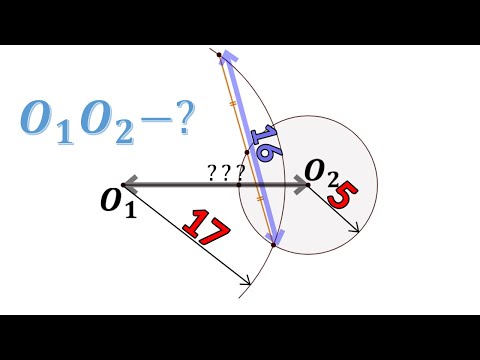 Относительное положение двух окружностейКонцентрические и эксцентрические круги. Два круга называются концентрическими, когда они имеют один общий центр, и эксцентрическими, когда из центры не совпадают. На чертеже 96 представлены круги концентрические и на чертежах 97, 98, 99, 100 и 101 круги эксцентрические. Внешние и внутренние круги. Круги называются внешними, когда все точки одного лежат вне площади другого круга, и внутренними, когда все точки одного лежат внутри площади другого круга. На чертежах 97 и 99 изображены круги внешние, на чертежах 96, 98 и 100 круги внутренние. Касательные окружности. Окружности называются касательными, когда они имеют одну общую точку. Общая точка двух касательных окружностей называется их точкой соприкосновения. Соприкосновение называется внешним, когда два круга, имея общую точку, лежат один вне другого, и внутренним, когда один круг лежит внутри другого. На черт. 99 имеем случай внешнего, а на чертеже 100 случай внутреннего соприкосновения. Пересекающиеся окружности. Окружности называются пересекающимися, когда они имеют две общие точки (черт. 101). Линия центров есть отрезок, соединяющий центры двух кругов. Теорема 71. Две окружности, имеющие общую точку на линии центров, другой общей точки иметь не могут. Дано. Две окружности с центрами O и O’ имеют общую точку A (черт. 102). Требуется доказать, что другой общей точки у них нет. Доказательство. Положим, существует другая общая точка B, следовательно, OB = OA и O’B = O’A. Складывая эти равенства, мы имели бы OB + O’B = OA + O’A или равенство несообразное, ибо ломаная не может равняться прямой. Итак, другой общей точки быть не может (ЧТД). Теорема 72. Две окружности, имеющие одну общую точку вне линии центров, имеют и другую общую точку по другую сторону линии центров. Дано. Две окружности, центры которых O и O’, имеют общую точку A вне отрезка OO’ (черт. 103), соединяющей центры. Требуется доказать, что существует и другая общая точка по другую сторону центров. Доказательство. Из точки A опустим на линию центров перпендикуляр AG и на продолжении его отложим отрезок BG, равный AG. Докажем, что точка B будет другая общая точка. Точка B лежит на окружности O, ибо AO = BO как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’. Точка B лежит на окружности O’, ибо AO’ = BO’ как равные наклонные, находящиеся на равных расстояниях AG и BG от перпендикуляра OO’, следовательно, точка B есть другая общая точка (ЧТД). Теорема 73. Если две окружности пересекаются в двух точках, то линия центров перпендикулярна и делит пополам хорду, соединяющую точки пересечения. Дано. Точки A и B есть точки пересечения (черт. 104) двух окружностей. Требуется доказать, что AG = BG и AB ⊥ OO’. Доказательство. Треугольники OAO’ и OBO’ равны, ибо OO’ сторона общая. OA = OB как радиусы окружности O. O’A = O’B как радиусы окружности O’. Треугольники AOG и BOG равны, ибо OG сторона общая, AO = BO как радиусы, ∠AOG = ∠BOG по доказанному. Следовательно, AG = BG (хорда AB делится линией центров пополам), ∠AGO = ∠BGO (хорда AB перпендикулярна к линии центров). Таким образом, хорда AB делится пополам и перпендикулярна к линии центров OO’ (ЧТД). Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать  Расстояние между центрами окружностей1. Если две окружности пересекаются в двух точках, расстояние центров меньше суммы и больше разности радиусов. Действительно, с одной стороны (черт. 104) 2. Если две окружности касаются, расстояние центров равно сумме радиусов, если соприкосновение внешнее, и разности радиусов, если соприкосновение внутреннее. Из чертежа 105 видно, что а из чертежа 106 3. Если одна окружность лежит вне другой, расстояние центров больше суммы радиусов. Из чертежа 107 видно, что 4. Если окружность лежит одна внутри другой, расстояние центров меньше разности радиусов. Действительно, из чертежа 108 видно, что Для того, чтобы имело место равенство, нужно дробь во второй части неравенства (1) увеличить. Для этого следует ее знаменатель уменьшить. Положим, мы нашли, что имеет место равенство Разделим дугу AB на равное число таких частей, чтобы каждая часть была менее GF; тогда одна из точек деления i упадет в промежутке между G и F. Дуги AB и Ai соизмеримы, следовательно, Разделив равенства (b) на (a), находим равенство несообразное, ибо первая часть его больше, а вторая меньше 1, следовательно, допущение (1) не имеет места. AOB/AOF ∆ ObC ибо они, будучи прямоугольными, имеют по равной гипотенузе OC, OD, OA, OB и равным катетам, следовательно, aC = bC 📺 ВидеоГеометрия Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружСкачать  Расстояние между центрами. Окружность. Математика 10-11 классы.Скачать  Как найти расстояние между центрами | Олимпиадная математикаСкачать  9 класс, 8 урок, Взаимное расположение двух окружностейСкачать  Радиус и диаметрСкачать  Математика Радиусы двух пересекающихся окружностей равны 17 см и 39 см, а расстояние между ихСкачать  Уравнение окружности (1)Скачать  9 класс, 6 урок, Уравнение окружностиСкачать  Окружность вписанная в треугольник и описанная около треугольника.Скачать  Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать  |