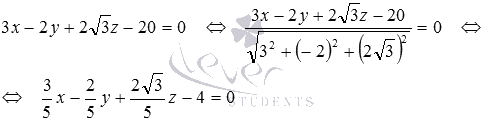Расстояние между параллельными плоскостями равно расстоянию от любой прямой одной верно ли

В этой статье содержится ответ на вопрос: «Как найти расстояние между двумя параллельными плоскостями методом координат»? Сначала дано определение расстояния между параллельными плоскостями. Далее получена формула, позволяющая вычислять расстояние между параллельными плоскостями, которые заданы в прямоугольной системе координат. В заключении разобраны решения примеров и задач на нахождение расстояния между параллельными плоскостями.

Навигация по странице.

Видео:Расстояние между параллельными прямымиСкачать

Расстояние между двумя параллельными плоскостями – определение.

Расстояние между двумя параллельными плоскостями определяется через расстояние от точки до плоскости. Покажем, как это делается.

Рассмотрим две параллельные плоскости и . Возьмем на любой из этих плоскостей точку М₁ и опустим перпендикуляр М₁H₁ из этой точки на другую плоскость. Длина перпендикуляра M₁H₁ является расстоянием между параллельными плоскостями и .

Расстояние между параллельными плоскостями – это расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.

Такое определение расстояния между параллельными плоскостями не случайно. Оно тесно связано со следующей теоремой.

Все точки одной из параллельных плоскостей находятся на одинаковом расстоянии от другой плоскости.

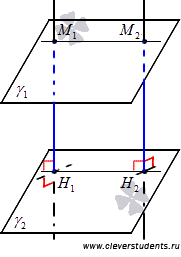
Пусть нам даны две параллельные плоскости и . Чтобы доказать эту теорему нам нужно доказать, что два перпендикуляра М₁H₁ и M₂H₂ , проведенные из различных точек М₁ и М₂ одной из заданных параллельных плоскостей к другой плоскости, имеют одинаковую длину.

Прямые М₁H₁ и M₂H₂ параллельны, так как они перпендикулярны к одной плоскости. Из аксиомы о единственной плоскости, проходящей через три различные точки, не лежащие на одной прямой, следует, что через две параллельные прямые проходит единственная плоскость (об этом мы упоминали в разделе способы задания плоскости). Тогда будем считать, что через параллельные прямые M₁H₁ и M₂H₂ проходит плоскость . Очевидно, плоскость пересекает плоскости и по прямым М₁М₂ и H₁H₂ . Эти прямые не пересекаются (в противном случае плоскости и имели бы общую точку, что невозможно, так как они параллельны по условию), значит, они параллельны. Таким образом, в четырехугольнике М₁М₂H₂H₁ противоположные стороны попарно параллельны, следовательно, М₁М₂H₂H₁ — параллелограмм (в нашем случае прямоугольник). Следовательно, его противоположные стороны равны. То есть, , что и требовалось доказать.

Следует отметить, что расстояние между параллельными плоскостями является наименьшим из расстояний между произвольными точками этих параллельных плоскостей.

Видео:10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Нахождение расстояния между параллельными плоскостями – теория, примеры, решения.

Переходим к вопросу нахождения расстояния между параллельными плоскостями.

На уроках геометрии в 10-11 классах расстояние между параллельными плоскостями находится примерно так: строится какой-нибудь перпендикуляр от некоторой точки одной плоскости к другой плоскости и определяется его длина. Для этого, в зависимости от условий задачи, применяется либо теорема Пифагора, либо признаки равенства или подобия соответствующих треугольников, либо определения синуса, косинуса, тангенса угла.

Если же есть возможность ввести прямоугольную систему координат и заданные параллельные плоскости описать с помощью уравнений, то расстояние между параллельными плоскостями можно отыскать методом координат. Давайте детально его разберем.

Сформулируем условие задачи.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и заданы две параллельные плоскости и . Требуется найти расстояние между этими параллельными плоскостями.

Решение будем строить на основе определения расстояния между параллельными плоскостями.

Так как в условии задачи определены плоскости и , то мы можем отыскать координаты некоторой точки М₁ , лежащей на одной из заданных плоскостей (для определенности будем считать, что точка лежит в плоскости ). Также мы можем получить нормальное уравнение плоскости в виде . Тогда искомое расстояние между параллельными плоскостями равно расстоянию от точки до плоскости , которой соответствует нормальное уравнение вида . Это расстояние вычисляется по формуле (ее вывод смотрите в разделе вычисление расстояния от точки до плоскости).

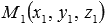
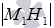
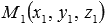
Итак, чтобы найти расстояние между двумя параллельными плоскостями нужно:

• определить координаты точки М₁ , лежащей в одной из заданных плоскостей;
• найти нормальное уравнение другой плоскости в виде ;
• вычислить искомое расстояние по формуле .

В частности, если в прямоугольной системе координат Oxyz плоскости соответствует общее уравнение плоскости , а плоскости — общее уравнение плоскости вида , то расстояние между параллельными плоскостями и вычисляется по формуле .

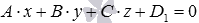
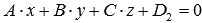
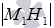
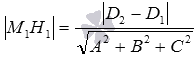
Поясним, как была получена эта формула.

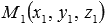
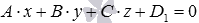
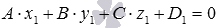
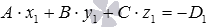
Пусть точка лежит в плоскости . Тогда координаты точки М₁ удовлетворяют уравнению плоскости , то есть, справедливо равенство , откуда имеем . Это равенство мы используем позже.

Нормальное уравнение плоскости в зависимости от знака числа D₂ имеет вид или . Но при любом значении числа D₂ расстояние от точки до плоскости можно вычислить по формуле . Учитывая полученное выше равенство , последняя формула примет вид .

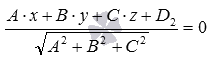
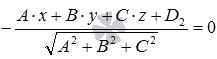
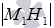
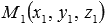
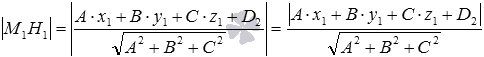
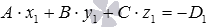
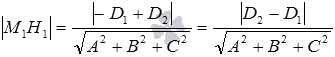
Осталось разобрать решения нескольких примеров.

Найдите расстояние между параллельными плоскостями и , которые в прямоугольной системе координат Oxyz определены уравнениями и соответственно.

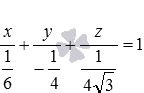
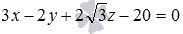
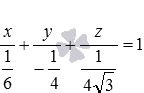
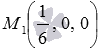
Заданное уравнение плоскости в отрезках вида позволяет легко найти координаты точки М₁ , лежащей в этой плоскости. В качестве точки М₁ возьмем точку, в которой плоскость пересекает ось Ox , то есть, .

Приведем общее уравнение плоскости к нормальному виду:

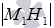
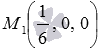
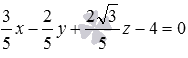
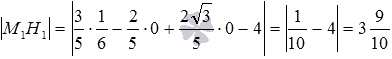
Теперь вычисляем расстояние от точки до плоскости :
.

Это и есть искомое расстояние между заданными параллельными плоскостями.

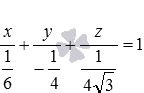
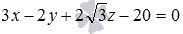
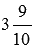
От уравнения плоскости в отрезках перейдем к общему уравнению плоскости: . Чтобы коэффициенты при переменных x , y и z в общих уравнениях плоскостей и стали равными, умножим обе части второго уравнения на два: . Теперь мы можем воспользоваться формулой для вычисления расстояния между параллельными плоскостями: .

.

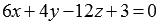
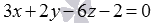
Вычислите расстояние между параллельными плоскостями и .

Очевидно, при таком условии задачи удобно использовать второй способ для нахождения расстояния между параллельными плоскостями. Если умножить обе части второго уравнения плоскости на два, то коэффициенты при переменных x , y и z в уравнениях 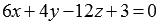и станут равны и можно будет применить формулу: .

Несомненно, можно было использовать первый способ.

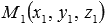
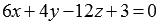
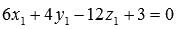
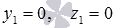
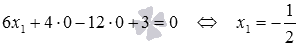
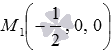
Пусть точка лежит в плоскости , тогда ее координаты удовлетворяют уравнению плоскости, то есть, справедливо равенство . Приняв , вычислим x₁ : . Следовательно, .

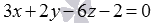
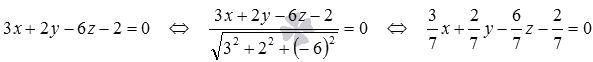
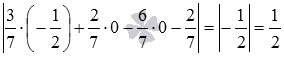
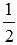
Теперь приведем общее уравнение плоскости к нормальному виду: . Тогда искомое расстояние между параллельными плоскостями равно .

.

Видео:Расстояние между параллельными плоскостямиСкачать

Теоретические самостоятельные работы по геометрии

Теоретические самостоятельные работы по геометрии

Подготовила учитель математики

МОУ Дугдинская СОШ

Проверочная работа №1.

Аксиомы стереометрии и следствия из них

1. Верно ли, что если концы отрезка лежат в данной плоскости, то и его середина лежит в данной плоскости?

2. Могут ли две плоскости иметь общую точку, но не иметь общей прямой?

3. Точка А не лежит в плоскости KMN. Назовите прямую пересечения плоскостей AMN и AKM.

4. Даны точки А, В, С и D. Плоскость α проходит через прямую АВ, но не проходит через точку С. Прямые AD и ВС пересекаются в точке В. Сколько данных точек лежит в плоскости α?

5. В пространстве даны прямая и точка. Сколько различных плоскостей можно через них провести?

6. *Верно ли, что если три данные точки лежат в одной плоскости, то они не лежат на одной прямой?

7. *Могут ли три прямые иметь общую точку, но не лежать в одной плоскости?

8. *Три прямые пересекаются в точке А. Через данную точку необходимо провести плоскость, содержащую ровно две из трех данных прямых.

Сколько таких плоскостей можно провести? Рассмотрите все возможные случаи.

одну или бесконечно много

три или не одной

Проверочная работа №2.

Параллельные прямые в пространстве.

Параллельность прямой и плоскости

1. Верно ли, что две параллельные прямые лежат в одной плоскости?

2. Может ли прямая, параллельная плоскости, пересекать какую-либо прямую этой плоскости?

3. Определите взаимное расположение прямой а и плоскости α, если:

a || b и прямая b пересекает плоскость α.

4. Дана плоскость β и прямые а, b, с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если:

а || с , прямые b и с пересекаются, а прямая с лежит в плоскости β.

5. Может ли прямая в пространстве пересекать одну из двух параллельных прямых, но не пересекать другую?

6. Определите взаимное расположение прямой а и плоскости α, если в плоскости α не существует прямой, пересекающей а.

7. Верно ли, что две прямые, параллельные одной плоскости, параллельны?

8. Могут ли прямые AB и CD быть параллельными, если прямые AD и BC пересекаются?

Проверочная работа №3.

Взаимное расположение прямых в пространстве

1. Верно ли, что если две прямые в пространстве не пересекаются, то они параллельны?

2. Может ли угол в пространстве быть тупым?

3. Определите взаимное расположение прямых a и b , если прямая а лежит в плоскости α, а прямая b пересекает плоскость α в точке, не лежащей на прямой а.

4. Прямая l пересекает плоскость треугольника АВС в точке В. Назовите прямую, скрещивающуюся с l и содержащую сторону данного треугольника.

5. Определите, верно ли на плоскости, в пространстве или и на плоскости, и в пространстве данное утверждение:

«Если две различные прямые не пересекаются, то они параллельны.

6. Верно ли, что две прямые, параллельные одной плоскости, могут быть скрещивающимися?

7. Могут ли в пространстве два угла с соответственно параллельными сторонами не быть равными?

8. Определите, какой из случаев взаимного расположения прямых a и b невозможен, если прямая а пересекается с с, а b||с.

Проверочная работа №4.

Тетраэдр и параллелепипед

1. Верно ли, что прямая, лежащая в одной из двух параллельных плоскостей, параллельна второй плоскости?

2. Могут ли рёбра тетраэдра лежать на параллельных прямых?

3. Параллельные плоскости α и β пересекают плоскость γ по прямым a и b соответственно. Определите взаимное расположение прямых a и b .

4. Определите вид сечения параллелепипеда плоскостью, проходящей через середины четырёх боковых рёбер.

5. Дана плоскость α и точка А вне данной плоскости. Определите, какую фигуру в пространстве образуют все прямые, параллельные данной плоскости и проходящие через данную точку. Как расположена эта фигура по отношению к плоскости α?

6. Верно ли, что если в каждой из двух параллельных плоскостей проходит прямая, то эти прямые скрещивающиеся?

7. Может ли в тетраэдре DABC грань DBC содержать прямую, параллельную ребру DA?

8. Плоскость γ пересекает параллельные плоскости α и β по прямым a и b соответственно. Прямая с скрещивается с прямой b . Укажите, какой из случаев взаимного расположения прямых а и с невозможен.

9. Определите, какую фигуру в пространстве образуют середины всех отрезков с концами на двух данных скрещивающихся прямых. Как расположена эта фигура по отношению к данным прямым?

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

ТЕОРЕТИЧЕСКАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА ПО ГЕОМЕТРИИ — 10 класс

Видео:Видеоурок "Расстояние между прямыми в пространстве"Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

ТЕОРЕТИЧЕСКАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА

Проверочная работа №1.

Аксиомы стереометрии и

следствия из них

1. Верно ли, что если концы отрезка лежат в данной плоскости, то и его середина лежит в данной плоскости?

2. Могут ли две плоскости иметь общую точку, но не иметь общей прямой?

3. В пространстве даны прямая и точка. Сколько различных плоскостей можно через них провести?

4. *Верно ли, что если три данные точки лежат в одной плоскости, то они не лежат на одной прямой?

5. *Могут ли три прямые иметь общую точку, но не лежать в одной плоскости?

Проверочная работа №3.

Взаимное расположение прямых в пространстве

1. Верно ли, что если две прямые в пространстве не пересекаются, то они параллельны?

2. Может ли угол в пространстве быть тупым?

3. Верно ли, что две прямые, параллельные одной плоскости, могут быть скрещивающимися?

4. Могут ли в пространстве два угла с соответственно параллельными сторонами не быть равными?

Проверочная работа №6.

Перпендикуляр и наклонные.

1. Верно ли, что длина перпендикуляра меньше длины наклонной, проведённой из этой же точки?

2. Может ли угол между прямой и плоскостью быть тупым?

3. *Верно ли, что расстояние между параллельными плоскостями равно расстоянию от любой прямой одной плоскости до другой плоскости?

4. *Могут ли две прямые, образующие с данной плоскостью неравные углы, быть параллельными?

Проверочная работа №7.

1. Верно ли, что любая прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна к другой плоскости?

2. Может ли диагональ прямоугольного параллелепипеда быть меньше одного из рёбер?

ТЕОРЕТИЧЕСКАЯ САМОСТОЯТЕЛЬНАЯ РАБОТА

Проверочная работа №1.

Аксиомы стереометрии и

следствия из них

1. Верно ли, что если концы отрезка лежат в данной плоскости, то и его середина лежит в данной плоскости?

2. Могут ли две плоскости иметь общую точку, но не иметь общей прямой?

3. В пространстве даны прямая и точка. Сколько различных плоскостей можно через них провести?

4. *Верно ли, что если три данные точки лежат в одной плоскости, то они не лежат на одной прямой?

5. *Могут ли три прямые иметь общую точку, но не лежать в одной плоскости?

Проверочная работа №2.

Параллельные прямые в пространстве.

Параллельность прямой и плоскости

1. Верно ли, что две параллельные прямые лежат в одной плоскости?

2. Может ли прямая, параллельная плоскости, пересекать какую-либо прямую этой плоскости?

3. Может ли прямая в пространстве пересекать одну из двух параллельных прямых, но не пересекать другую?

4. Верно ли, что две прямые, параллельные одной плоскости, параллельны?

Проверочная работа №4.

Тетраэдр и параллелепипед

1. Верно ли, что прямая, лежащая в одной из двух параллельных плоскостей, параллельна второй плоскости?

2. Могут ли рёбра тетраэдра лежать на параллельных прямых?

3. Верно ли, что если в каждой из двух параллельных плоскостей проходит прямая, то эти прямые скрещивающиеся?

Проверочная работа №5.

Перпендикулярность прямой и плоскости

1. Верно ли, что две прямые, перпендикулярные к одной плоскости, параллельны?

2. Может ли прямая, перпендикулярная к плоскости, быть параллельной прямой, лежащей в этой плоскости?

3. Могут ли две скрещивающиеся прямые быть перпендикулярными к одной плоскости?

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Видео:7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 342 человека из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 689 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Контрольная работа по геометрии по теме: «Параллельность прямой и плоскости» -10 класс

Кроссенс по геометрии на тему «Средняя линия трапеции» (9 класс)

Конспекты по кыргызского языка на тему» Айдана»

Тест по кыргызского языка на тему»Коп бурчтук»

Конспект по кыргызского языка на тему» Коп бурчтук»

Презентация урока по теме «Решение задач по теореме Пифагора»

Урок (план и технологическая карта) по геометрии на тему «Вычитание векторов» (9 класс)

«Задачи для игры «Лото»»

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5442218 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ

Время чтения: 1 минута

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

💥 Видео

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Геометрия 7 класс (Урок№26 - Расстояние от точки до прямой. Расстояние между параллельными прямыми.)Скачать

9. Угол между плоскостями Условия параллельности и перпендикулярности плоскостейСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Параллельность прямой и плоскости. 10 класс.Скачать

7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

6 серия "Расстояние между параллельными плоскостями" из курса видеолекций "Метод координат"Скачать

Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Расстояние от точки до плоскости / Вывод формулыСкачать

✓ Как решать стереометрию | ЕГЭ-2023. Математика. Профильный уровень. Задание 13 | Борис ТрушинСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

10 класс, 10 урок, Параллельные плоскостиСкачать

Расстояние между скрещивающимися прямыми (вводный урок)Скачать