Расположение центров вписанной и описанной окружностей

Ключевые слова: окружность, описанная окружность, центр окружности, вписанная окружность, треугольник, четырехугольник, вневписанная окружность

Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.

Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.

Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
Сам многоугольник в таком случае называется описанным около данной окружности.
Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.

Для произвольного многоугольника невозможно вписать в него и описать около него окружность.
Для треуголь ника это всегда возможно.

Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности

• Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
• В любой треугольник можно вписать окружность, и только одну.
• Радиус вписанной в треугольник окружности равен отношению площади треугольника и его полупериметра: $$r = frac

  $$ , где S — площадь треугольника, а $$p =frac$$ — полупериметр треугольника.

Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.

Окружность называется описанной около треугольника, если она проходит через три его вершины.

• Вокруг любого треугольника можно описать окружность, и только одну.
• В любом треугольнике сторона равна произведению диаметра описанной окружности и синуса противолежащего угла.
• Площадь треугольника равна отношению произведения длин всех его сторон к учетверенному радиусу окружности, описанной около этого треугольника: $$R =frac$$, где S — площадь треугольника.

• Центр вневписанной окружности лежит на пересечении биссектрис внешних углов, при вершинах касаемой стороны, и биссектрисы угла при третей вершине.

Окружность, вписанная в прямоугольный треугольник

• Радиус вписанной окружности находят по формулам: $$r = frac$$, и $$r = frac$$, где a и b катеты прямоугольного треугольника, а c гипотенуза прямоугольного треугольника.

Окружность, описанная около прямоугольного треугольника

• Центр описанной окружности совпадает с серединой гипотенузы.
• Радиус равен половине гипотенузы: $$R = frac$$.
• Радиус равен медиане, проведенной к гипотенузе: $$R = m_$$.

Четырехугольник, вписанный в окружность

• Четырехугольник можно вписать в окружность, если сумма противолежащих углов равна $$180^circ: alpha + beta + gamma +delta = 180^circ$$.
• Если четырехугольник вписан в окружность, то суммы противолежащих углов равны $$180^circ$$.
• Сумма произведений противолежащих сторон четырехугольника ABCD равна произведению диагоналей: $$ABcdot DC + AD cdot BC = BD cdot AC$$.
• Площадь: $$S = sqrt$$, где $$p = frac$$ — полупериметр четырехугольника.

Окружность, вписанная в ромб

• В любой ромб можно вписать окружность.
• Радиус r вписанной окружности: $$r = frac$$, где h — высота ромба или $$r = frac <d_cdot d_>$$, где a — сторона ромба, d₁ и d₂ — диагонали ромба.

Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Описанная и вписанная окружность

теория по математике 📈 планиметрия

Видео:ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Описанная окружность

Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.

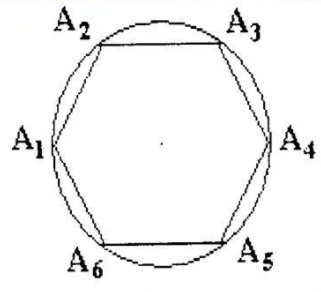
Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Вписанная окружность

Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.

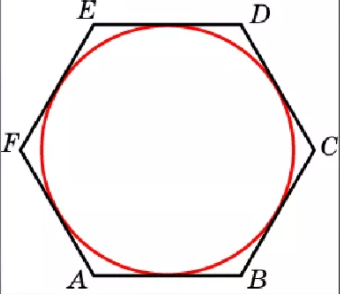
В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.

Вписанный и описанный треугольники

Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.

В любой треугольник можно вписать окружность: 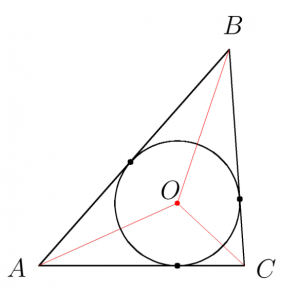Центр вписанной окружности

Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.

Вписанный и описанный четырехугольники

Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.

Условие вписанной в 4-х угольник окружности

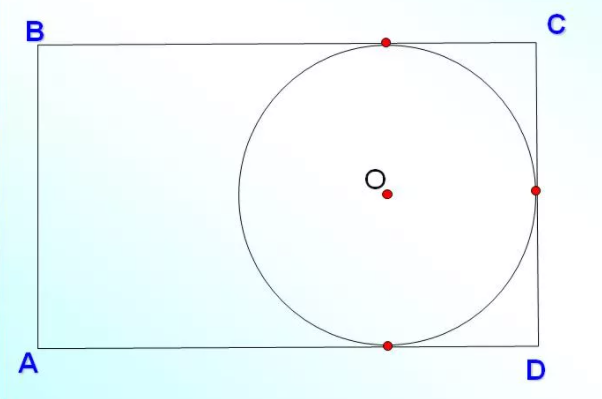
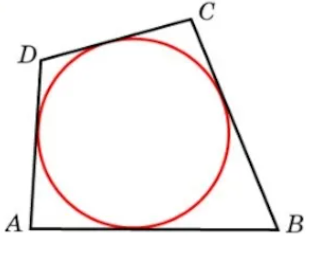
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.

На рисунке выполняется данное условие, то есть AD + BC=DC + AB

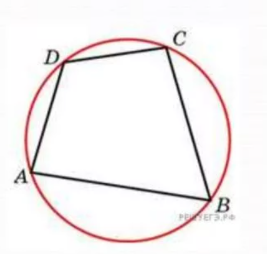
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.

На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вписанные и описанные окружности

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом занятии мы изучим вписанные и описанные окружности. Для начала дадим определение вписанной окружности, поговорим об ее основных свойствах. Также рассмотрим варианты описанной окружности, перечислим ее главные свойства. Используя полученные сведения, вместе с преподавателем решим несколько примеров на эту тему.

🌟 Видео

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Расстояние между центрами вписанной и описанной окружностей треугольника и их радиусами #ShortsСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанная и описанная окружности. ЗадачиСкачать

Геометрия. 9 класс. Формулы для нахождения радиусов вписанной и описанной окружностей треугольникаСкачать

Вписанная и описанная окружностиСкачать

Геометрия 6. Радиусы вписанной и описанной окружностей.Скачать

Построить описанную окружность (Задача 1)Скачать

8 класс, 38 урок, Вписанная окружностьСкачать

Радиус описанной окружностиСкачать

Описанная и вписанная окружности треугольника - 7 класс геометрияСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

М1152. Расстояние между центрами вписанной и описанной окружностейСкачать

ОПИСАННАЯ и ВПИСАННАЯ окружности. §21 геометрия 7 классСкачать

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать