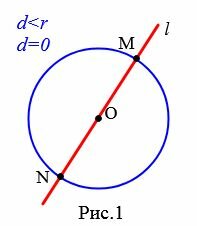
Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.
Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.
  |
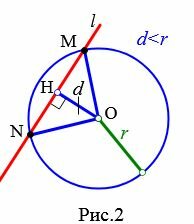Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
В этом случае прямая называется секущей по отношению к окружности.
Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.
 |
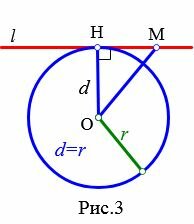Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.
Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.
 |
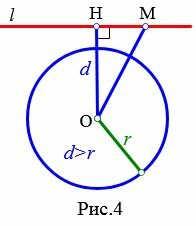Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Отрезки и прямые, связанные с окружностью. Теорема о бабочке
 Отрезки и прямые, связанные с окружностью |
| Свойства хорд и дуг окружности |
| Теоремы о длинах хорд, касательных и секущих |
| Доказательства теорем о длинах хорд, касательных и секущих |
| Теорема о бабочке |
Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать
Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства | ||||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||||
| Круг |  | |||||||||||||||||||||||||||
| Радиус |  | |||||||||||||||||||||||||||
| Хорда |  | |||||||||||||||||||||||||||
| Диаметр |  | |||||||||||||||||||||||||||
| Касательная |  | |||||||||||||||||||||||||||
| Секущая |  | |||||||||||||||||||||||||||
| Окружность |
|
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Конечная часть плоскости, ограниченная окружностью
Отрезок, соединяющий центр окружности с любой точкой окружности
Отрезок, соединяющий две любые точки окружности
Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности
Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания
Прямая, пересекающая окружность в двух точках
Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать
Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
|
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Большая из двух хорд расположена ближе к центру окружности.
У равных дуг равны и хорды.
Дуги, заключённые между параллельными хордами, равны.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать
Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема | ||||||||||||||||
| Пересекающиеся хорды |  | |||||||||||||||||
| Касательные, проведённые к окружности из одной точки |  | |||||||||||||||||
| Касательная и секущая, проведённые к окружности из одной точки |  | |||||||||||||||||
| Секущие, проведённые из одной точки вне круга |  | |||||||||||||||||
| Пересекающиеся хорды | ||
| ||
| Касательные, проведённые к окружности из одной точки | ||
| ||
| Касательная и секущая, проведённые к окружности из одной точки | ||
| ||
| Секущие, проведённые из одной точки вне круга | ||
| ||
| Пересекающиеся хорды |
|
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать
Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать
Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
Видео:Взаимное расположение прямой и окружности | Геометрия 7-9 класс #68 | ИнфоурокСкачать
Геометрия. 8 класс
Конспект
Рассмотрим окружность с центром в точке О и прямую a, её не пересекающую.
Расстояние от центра окружности до прямой равно длине перпендикуляра ОВ.
Это расстояние больше радиуса окружности.
Будем перемещать прямую, параллельно самой себе в сторону центра окружности. В определённый момент, прямая коснется окружности.
Расстояние от центра окружности до прямой равно радиусу окружности.
Прямая, имеющая с окружностью только одну общую точку называется касательной к окружности.
Общая точка прямой и окружности называется точкой касания.
Будем передвигать прямую далее к центру. Прямая пересечет окружность в двух точках.
Расстояние от центра окружности до прямой меньше радиуса.
Продолжая движение дальше, мы получим еще одну касательную к окружности.
Продолжим движение прямой дальше, она опять не будет иметь с окружностью общих точек.
Расстояние от центра окружности опять больше её радиуса.
Рассмотрим случай, когда прямая имеет с окружностью одну общую точку.
Сформулируем свойство касательной.
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Дано: Окружность с центром О, a – касательная, B – точка касания.
Доказать: a ⊥ OB
Доказательство:
Пусть утверждение неверно, т.е. прямая a не перпендикулярна радиусу OB. Тогда OB – наклонная к прямой a. Перпендикуляр меньше наклонной, тогда расстояние от центра O до прямой a меньше радиуса. Следовательно, прямая a и окружность имеют 2 общие точки. Но это противоречит условию, т.к. прямая a – касательная. Значит наше предположение неверно и a ⊥ OB.
Верно и обратное утверждение:
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Проведем к окружности две касательные из одной точки, не принадлежащей окружности.
Выполняется утверждение:
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Докажите его самостоятельно, используя равенство треугольников AOВ и AOС.
Дано: окружность с центром O, касательные AB и AC
Доказать: AB = AC, ∠OAB = ∠OAC
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.
🎦 Видео
Геометрия 8 класс (Урок№25 - Взаимное расположение прямой и окружности.)Скачать
70. Взаимное расположение прямой и окружностиСкачать
Взаимное расположение окружностей. 7 класс.Скачать
Стереометрия 10 класс. Часть 1 | МатематикаСкачать
Урок по геометрии ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИСкачать
Окружность. 7 класс.Скачать
Геометрия 8 класс : Взаимное расположение прямой и окружностиСкачать
Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать
9 класс, 8 урок, Взаимное расположение двух окружностейСкачать
Теорема о числе точек пересечения окружности и прямойСкачать
Взаимное расположение прямой и окружности, математика 6 классСкачать
Геометрия. 7 класс. Взаимное расположение прямой и окружности /13.04.2021/Скачать
9 класс, 7 урок, Уравнение прямойСкачать
