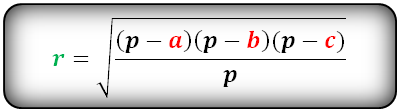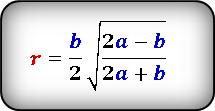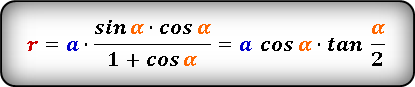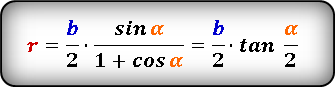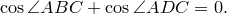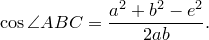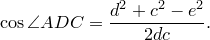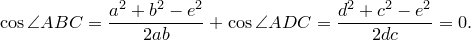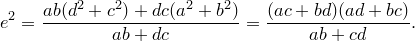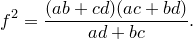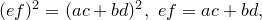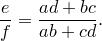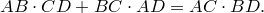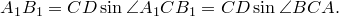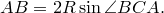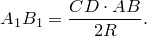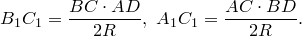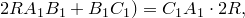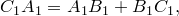Радиусы окружностей в разных фигурах

Видео:Найти центр и радиус окружностиСкачать

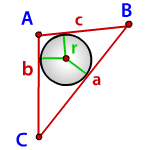
Радиус вписанной окружности в треугольник

a , b , c — стороны треугольника

p — полупериметр, p=( a + b + c )/2

Формула радиуса вписанной окружности в треугольник ( r ):

Видео:Радиус и диаметрСкачать

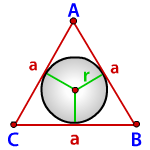
Радиус вписанной окружности в равносторонний треугольник

a — сторона треугольника

r — радиус вписанной окружности

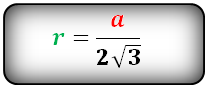
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

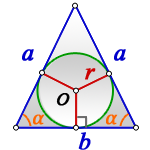
Радиус вписанной окружности равнобедренный треугольник

1. Формулы радиуса вписанной окружности если известны: стороны и угол

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

α — угол при основании

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :

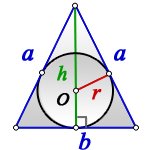
2. Формулы радиуса вписанной окружности если известны: сторона и высота

a — равные стороны равнобедренного треугольника

b — сторона ( основание)

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :

Видео:Радиус описанной окружностиСкачать

Как найти радиус окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Видео:Радиус описанной окружности трапецииСкачать

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.

Видео:1 2 4 сопряжение окружностейСкачать

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Видео:Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Видео:КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Видео:Окружность и круг, 6 классСкачать

Разные виды окружностей и теоремы, с ними связанные.

Окружностью называется геометрическая фигура, состоящая из всех точек плоскости,расположенных на заданном расстоянии от данной точки

Вписанная и описанная окружность, формулы для вычисления радиусов, площадей.

Окружность Аполлония — геометрическое место точек плоскости, отношение расстояний от которых до двух заданных точек — величина постоянная, не равная единице.

Биполярные координаты — ортогональная система координат на плоскости, основанная на кругах Аполлония.

Пусть на плоскости даны две точки A и B. Рассмотрим все точки P этой плоскости, для каждой из которых

где k — фиксированное положительное число. При k = 1 эти точки заполняют срединный перпендикуляр к отрезку AB; в остальных случаях указанное геометрическое место — окружность, называемая окружностью Аполлония.

Просмотр содержимого документа
«Разные виды окружностей и теоремы, с ними связанные.»

“А в окружность я влюбился и на ней остановился.”

Цель проекта: Изучить свойства, виды разных окружностей и теоремы, с ними связанные.

Я начал свою работу с того , что изучил свойства окружности в школьном курсе геометрии по учебнику А.В.Погорелова “Геометрия 7-9” и материал за рамками школьного курса. При сборе информации из различных источников и в работе над проектом я расширил свои знания и буду продолжать дальше изучать эту тему и делиться знаниями с одноклассниками и всеми , кому это интересно.

Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом. Замкнутый круг, не имеющий внутренное пространство.

Окружность диаметра AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом.

Окружность — это фигура, состоящая из всех точек плоскости, для каждой из которых отношение расстояний до двух данных точек равно данному числу, отличному от единицы. (см. Окружность Аполлония)

Также фигура, состоящая из всех таких точек, для каждой из которых сумма квадратов расстояний до двух данных точек равна заданной величине, большей половины квадрата расстояния между данными точками.

Радиус — не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из её точек.

Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром.

Окружность называется единичной, если ее радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.

Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

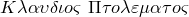
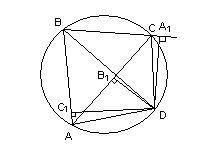
Клавдий Птолемей (), живший в конце первого — начале второго века н.э., был древнегреческим ученым-астрономом, математиком, астрологом, географом, оптиком и теоретиком музыки. Он известен как комментатор Евклида. Птолемей пытался доказать знаменитый Пятый постулат. Основной труд Птолемея — “Альмагест”, в котором он изложил сведения по астрономии. Включал “Альмагест” и каталог звездного неба.

Теорема Птолемея. Вокруг четырехугольника можно описать окружность тогда и только тогда, когда произведение его диагоналей равно сумме произведений его противоположных сторон.

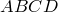
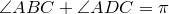
Доказательство необходимости. Поскольку четырехугольник вписан в окружность, то

, откуда

Из треугольника 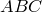по теореме косинусов находим

Аналогично из треугольника :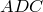

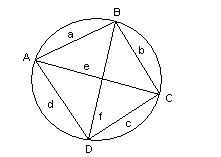
Сумма этих косинусов равна нулю:

Отсюда выразим :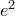

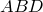
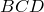
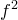
Рассмотрим треугольники и и найдем :

что и требовалось доказать.

Попутно мы доказали еще одно утверждение. Для четырехугольника, вписанного в окружность,

Доказательство достаточности. Пусть выполнено равенство

Докажем, что вокруг четырехугольника 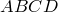можно описать окружность.

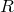
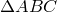
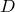
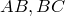
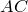
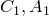
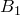
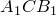
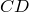
Обозначим через радиус окружности, описанной вокруг . Из точки опустим перпендикуляры на прямые и и обозначим точки пересечения этих прямых и перпендикуляров к ним через и соответственно. По теореме синсов для треугольника получаем (диаметр описанной окружности для этого треугольника равен ):

По теореме синусов для треугольника 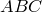имеем

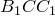
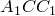
Таким же образом, рассматривая треугольники и получим соотношения

Отсюда, подставляя эти выражения в исходное равенство, имеем

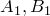
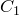
откуда следует, что точки и лежат на одной прямой.

Докажем теперь, что из этого следует, что вокруг четырехугольника 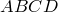можно описать окружность (достаточное условие теоремы Симсона).

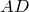
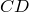
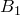
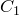
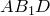
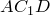
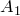
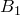
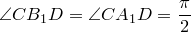
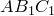
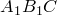
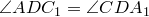
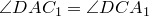
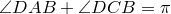
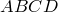
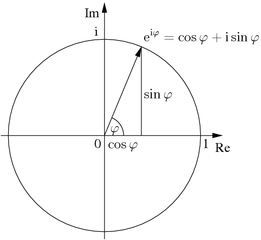
Построим окружности на отрезках и как на диаметрах. Первая из них проходит через точки и (углы и прямые), а вторая — через точки и (). Углы и равны как вертикальные, откуда следует, что , а значит, и . Отсюда , и вокруг четырехугольника можно описать окружность.

Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту с тригонометрическими функциями.

Формула Эйлера утверждает, что для любого вещественного числа x выполнено следующее равенство:

,

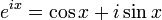
где e — основание натурального логарифма,

i — мнимая единица.

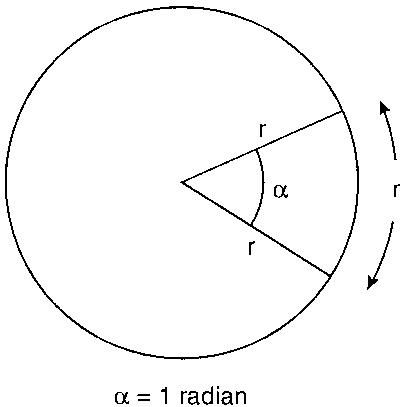
Угол, образуемый дугой окружности, равной по длине радиусу, принимается за 1 радиан.

Длина единичной полуокружности обозначается через π.

🔍 Видео

Уравнение окружности (1)Скачать

Радиус вписанной окружности #математика #егэ #математикапрофиль2023 #fyp #школаСкачать

Радиус вписанной окружности, формулу через площадь и полупериметрСкачать