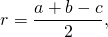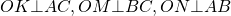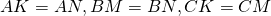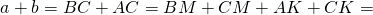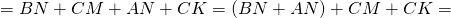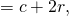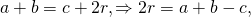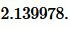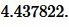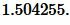Радиус вписанной в прямоугольный треугольник окружности равен
где a и b — катеты, c — гипотенуза.
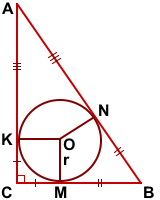
Проведём радиусы OK, OM, ON к сторонам треугольника.
(как отрезки касательных, проведённых из одной точки).
Отсюда следует, что четырёхугольник CKOM — квадрат, стороны которого равны радиусу вписанной в треугольник ABC окружности: CK=CM=OM=OK=r.
Таким образом, формула радиуса вписанной в прямоугольный треугольник окружности
- Решение №2414 Радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле r=(a+b-c)/2 …
- Радиус вписанной окружности в прямоугольный треугольник онлайн
- 1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
- 2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
- 3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
- 🔍 Видео
Видео:🔴 Радиус вписанной в прямоугольный треугольник ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать

Решение №2414 Радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле r=(a+b-c)/2 …
Радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле , где a и b – катеты, а c – гипотенуза. Пользуясь этой формулой, найдите c, если a = 20, b = 21 и r = 6.
Источник: ОГЭ Ященко 2022 (36 вар)
Подставим все значения в формулу и найдём с:
|·2
12 = 20 + 21 – c
12 = 41 – c
c = 41 – 12 = 29
Ответ: 29.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.8 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Видео:Формулы для радиуса окружности #shortsСкачать

Радиус вписанной окружности в прямоугольный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в прямоугольный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Радиус вписанной в прямоугольный треугольник окружности. 14 задание из ОГЭ по математикеСкачать

1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
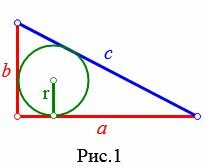 |
Радиус вписанной в треугольник окружности, если известна площадь треугольника S и полупериметр p вычисляется из следующей формулы (статья Радиус вписанной в треугольник окружности, формула (5)):
| ( small r= frac, ) | (1) |
| ( small p= frac. ) | (2) |
Площадь прямоугольного треугольника по катетам вычисляется из формулы:
| ( small S= large frac small cdot a cdot b. ) | (3) |
Подставляя (2) и (3) в (1) получим формулу вписанной в прямоугольный треугольник окружности:
| ( small r= large frac<fracab><frac(a+b+c)> ) ( small = large frac, ) | (4) |
| ( small c= sqrt. ) | (5) |
Из формулы (4) выведем другую эквивалентную формулу. Умножим числитель и знаменатель формулы (4) на ( small a+b-c ):
| ( small r= frac ) ( small = frac ) ( small = frac ) | (6) |
Учитывая (5), формулу (6) можно переписать так:
| ( small r= frac ) ( small = frac .) |
Таким образом другая формула вычисления радиуса вписанной в треугольник окружности имеет вид:
| ( small r= frac ,) | (7) |
где c вычисляется из (5).
Пример 1. Известны катеты прямоугольного треугольника a=17 и b=5. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (4) и (7). Вычислим, сначала, гипотенузу прямоугольного треугольника из формулы (5):
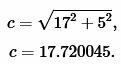 |
Подставим значения ( small a=17, ; b=5; c=17.720045 ) в (7):
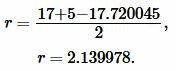 |
Ответ:
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
Пусть известны катет a прямоугольного треугольника и прилежащий к нему угол β(Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
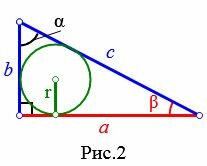 |
| ( small frac=frac .) |
Учитывая, что ( small alpha=90°-beta ) и ( small sin (90°-beta)=cos beta ), получим:
| ( small frac=frac ) ( small =frac=frac .) | (8) |
Тогда из (8) получим:
| ( small b=frac. ) | (9) |
Далее, из теоремы синусов:
| ( small frac=frac ) ( small =frac=frac .) |
| ( small c=frac .) | (10) |
Чтобы получить формулу радиуса вписанной в прямоугольный треугольник окружности через катет и прилежащий к нему угол, подставим значения ( small b ) и ( small c ) из (9) и (10) в (7):
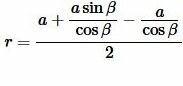 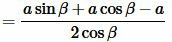 |
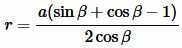 | (11) |
Пример 2. Известны катет ( small a=21 ) и прилежащий к нему угол ( small beta=30° ) прямоугольного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Подставим значения ( small a=21 ) ( small beta=30° ) в (11):
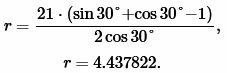 |
Ответ:
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
Пусть известны катет a прямоугольного треугольника и противолежащий угол ( small alpha; ) (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
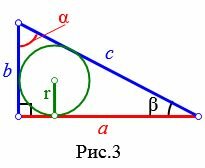 |
В предыдущем параграфе мы вывели формулу вписанной в прямоугольный треугольник окружности по катету и прилежащему углу (формула (11)). Учитывая, что в прямоугольном треугольнике сумма острых углов равна 90°, имеем:
| ( small alpha+beta=90°) ( small beta=90°-alpha ) |
Тогда (11) можно преобразовать так (подробнее на странице Формулы приведения тригонометрических функций:
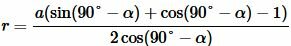 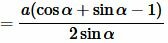 |
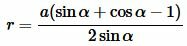 | (12) |
Пример 3. Известны катет ( small a=6 ) прямоугольного треугольника и противолежащий угол ( small alpha=53°. ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (12). Подставим значение ( small a=6, ; alpha=53° ) в (12):
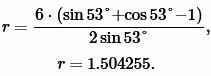 |
Ответ:
🔍 Видео
Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Радиус вписанной окружности, формулу через площадь и полупериметрСкачать

Формула радиуса вневписанной окружности в прямоугольный треугольник, касающейся катета.Скачать

Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

Важная формула для ЕГЭ! Радиус вписанной окружности для прямоугольного треугольникаСкачать
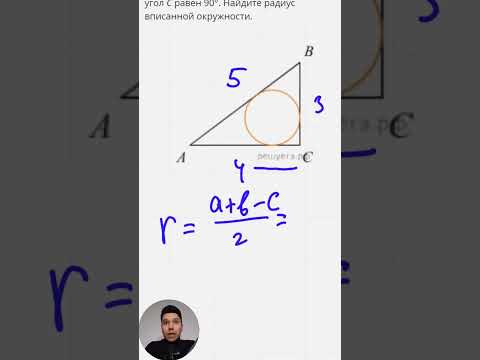
ОГЭ Задание 25 Окружность вписанная в прямоугольный треугольникСкачать

🔴 Площадь треугольника вычисляется по формуле ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать

Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

СТОРОНА КВАДРАТА через РАДИУС вписанной и описанной окружностейСкачать