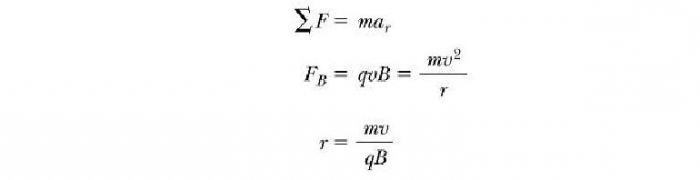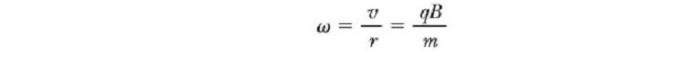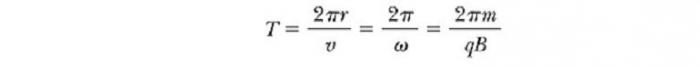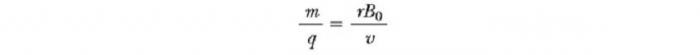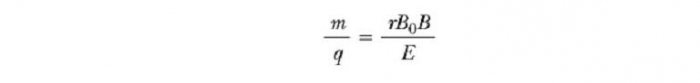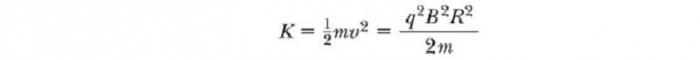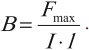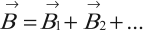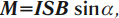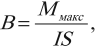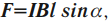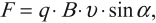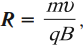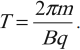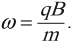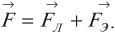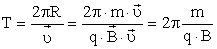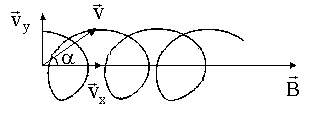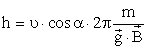Радиус окружности и период обращения заряда в магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Видео:Движение заряженной частицы в магнитном поле | 16 задание ЕГЭ | Магнитные поля в ЕГЭ по физикеСкачать

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
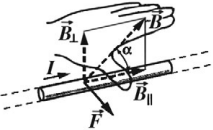
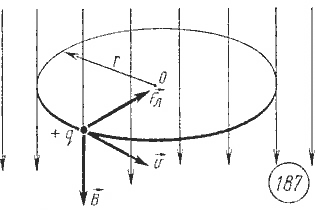
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Видео:Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Движение заряженных частиц в однородном магнитном поле

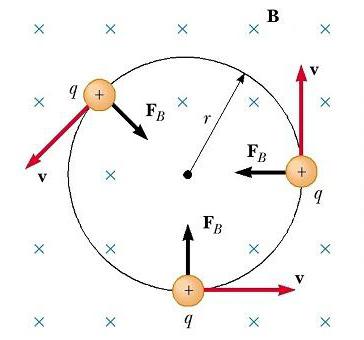
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Видео:26 задание ЕГЭ Движение частицы в магнитном поле | ЕГЭ по физике| Физика 11 классСкачать

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Видео:Движение заряженной частицы в поперечном магнитном полеСкачать

Движение частицы под углом к вектору магнитного поля

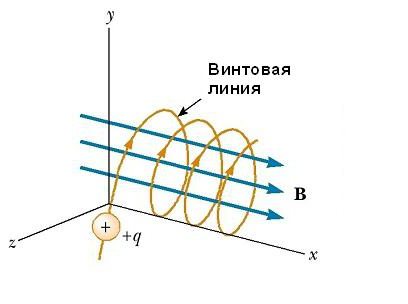
Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

Видео:Физика - движение по окружностиСкачать

Неоднородное магнитное поле: как в нем движутся частицы

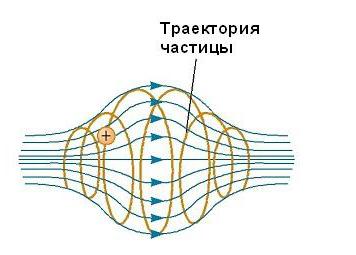
Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

Видео:55. Движение частиц в электромагнитных поляхСкачать

Как Земля влияет на движение космических частиц

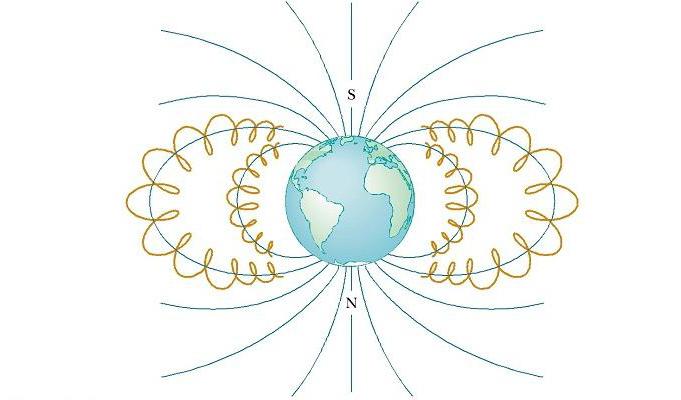
Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

Видео:Все виды движения в магнитном поле | Физика ЕГЭ 2023 | УмскулСкачать

Селектор скоростей

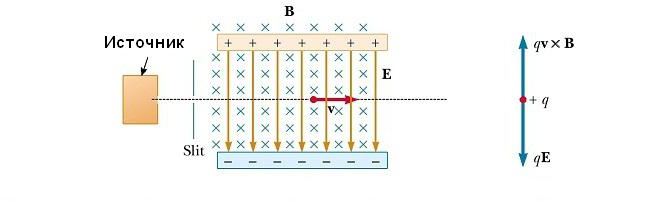
Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Видео:Тема 27. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Видео:Физика. 10 класс. Сила Лоренца. Движение заряженной частицы в магнитном поле /12.04.2021/Скачать

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

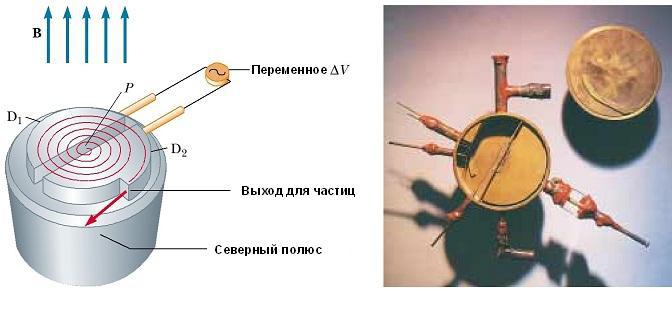
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т — время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один «удар» через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы — ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Видео:10 класс. Физика. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Видео:Урок 277. Масс-спектрограф. Циклотрон. Магнитный щит ЗемлиСкачать

Магнитное поле

Магнитное поле – особая форма материи, существующая вокруг движущихся электрических зарядов – токов.

Источниками магнитного поля являются постоянные магниты, проводники с током. Обнаружить магнитное поле можно по действию на магнитную стрелку, проводник с током и движущиеся заряженные частицы.

Для исследования магнитного поля используют замкнутый плоский контур с током (рамку с током).

Впервые поворот магнитной стрелки около проводника, по которому протекает ток, обнаружил в 1820 году Эрстед. Ампер наблюдал взаимодействие проводников, по которым протекал ток: если токи в проводниках текут в одном направлении, то проводники притягиваются, если токи в проводниках текут в противоположных направлениях, то они отталкиваются.

Свойства магнитного поля:

• магнитное поле материально;
• источник и индикатор поля – электрический ток;
• магнитное поле является вихревым – его силовые линии (линии магнитной индукции) замкнутые;
• величина поля убывает с расстоянием от источника поля.

Важно!
Магнитное поле не является потенциальным. Его работа на замкнутой траектории может быть не равна нулю.

Магнитным взаимодействием называют притяжение или отталкивание электрически нейтральных проводников при пропускании через них электрического тока.

Магнитное взаимодействие движущихся электрических зарядов объясняется так: всякий движущийся электрический заряд создает в пространстве магнитное поле, которое действует на движущиеся заряженные частицы.

Силовая характеристика магнитного поля – вектор магнитной индукции ​ ( vec ) ​. Модуль вектора магнитной индукции равен отношению максимального значения силы, действующей со стороны магнитного поля на проводник с током, к силе тока в проводнике ​ ( I ) ​ и его длине ​ ( l ) ​:

Обозначение – ( vec ) , единица измерения в СИ – тесла (Тл).

1 Тл – это индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила 1 Н.

Направление вектора магнитной индукции совпадает с направлением от южного полюса к северному полюсу магнитной стрелки (направление, которое указывает северный полюс магнитной стрелки), свободно установившейся в магнитном поле.

Направление вектора магнитной индукции можно определить по правилу буравчика:

если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции.

Для определения магнитной индукции нескольких полей используется принцип суперпозиции:

магнитная индукция результирующего поля, созданного несколькими источниками, равна векторной сумме магнитных индукций полей, создаваемых каждым источником в отдельности:

Поле, в каждой точке которого вектор магнитной индукции одинаков по величине и направлению, называется однородным.

Наглядно магнитное поле изображают в виде магнитных линий или линий магнитной индукции. Линия магнитной индукции – это воображаемая линия, в любой точке которой вектор магнитной индукции направлен по касательной к ней.

Свойства магнитных линий:

• магнитные линии непрерывны;
• магнитные линии замкнуты (т.е. в природе не существует магнитных зарядов, аналогичных электрическим зарядам);
• магнитные линии имеют направление, связанное с направлением тока.

Густота расположения позволяет судить о величине поля: чем гуще расположены линии, тем сильнее поле.

На плоский замкнутый контур с током, помещенный в однородное магнитное поле, действует момент сил ​ ( M ) ​:

где ​ ( I ) ​ – сила тока в проводнике, ​ ( S ) ​ – площадь поверхности, охватываемая контуром, ​ ( B ) ​ – модуль вектора магнитной индукции, ​ ( alpha ) ​ – угол между перпендикуляром к плоскости контура и вектором магнитной индукции.

Тогда для модуля вектора магнитной индукции можно записать формулу:

где максимальный момент сил соответствует углу ​ ( alpha ) ​ = 90°.

В этом случае линии магнитной индукции лежат в плоскости рамки, и ее положение равновесия является неустойчивым. Устойчивым будет положение рамки с током в случае, когда плоскость рамки перпендикулярна линиям магнитной индукции.

Видео:Урок 87 (осн). Вращательное движение. Период и частота вращенияСкачать

Взаимодействие магнитов

Постоянные магниты – это тела, длительное время сохраняющие намагниченность, то есть создающие магнитное поле.

Основное свойство магнитов: притягивать тела из железа или его сплавов (например стали). Магниты бывают естественные (из магнитного железняка) и искусственные, представляющие собой намагниченные железные полосы. Области магнита, где его магнитные свойства выражены наиболее сильно, называют полюсами. У магнита два полюса: северный ​ ( N ) ​ и южный ​ ( S ) ​.

Важно!
Вне магнита магнитные линии выходят из северного полюса и входят в южный полюс.

Разделить полюса магнита нельзя.

Объяснил существование магнитного поля у постоянных магнитов Ампер. Согласно его гипотезе внутри молекул, из которых состоит магнит, циркулируют элементарные электрические токи. Если эти токи ориентированы определенным образом, то их действия складываются и тело проявляет магнитные свойства. Если эти токи расположены беспорядочно, то их действие взаимно компенсируется и тело не проявляет магнитных свойств.

Магниты взаимодействуют: одноименные магнитные полюса отталкиваются, разноименные – притягиваются.

Видео:Движение заряженной частицы в магнитном поле 2021-1Скачать

Магнитное поле проводника с током

Электрический ток, протекающий по проводнику с током, создает в окружающем его пространстве магнитное поле. Чем больше ток, проходящий по проводнику, тем сильнее возникающее вокруг него магнитное поле.

Магнитные силовые линии этого поля располагаются по концентрическим окружностям, в центре которых находится проводник с током.

Направление линий магнитного поля вокруг проводника с током всегда находится в строгом соответствии с направлением тока, проходящего по проводнику.

Направление магнитных силовых линий можно определить по правилу буравчика: если поступательное движение буравчика (1) совпадает с направлением тока (2) в проводнике, то вращение его рукоятки укажет направление силовых линий (4) магнитного поля вокруг проводника.

При изменении направления тока линии магнитного поля также изменяют свое направление.

По мере удаления от проводника магнитные силовые линии располагаются реже. Следовательно, индукция магнитного поля уменьшается.

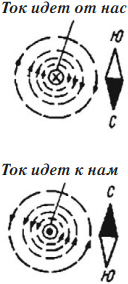
Направление тока в проводнике принято изображать точкой, если ток идет к нам, и крестиком, если ток направлен от нас.

Для получения сильных магнитных полей при небольших токах обычно увеличивают число проводников с током и выполняют их в виде ряда витков; такое устройство называют катушкой.

В проводнике, согнутом в виде витка, магнитные поля, образованные всеми участками этого проводника, будут внутри витка иметь одинаковое направление. Поэтому интенсивность магнитного поля внутри витка будет больше, чем вокруг прямолинейного проводника. При объединении витков в катушку магнитные поля, созданные отдельными витками, складываются. При этом концентрация силовых линий внутри катушки возрастает, т. е. магнитное поле внутри нее усиливается.

Чем больше ток, проходящий через катушку, и чем больше в ней витков, тем сильнее создаваемое катушкой магнитное поле. Магнитное поле снаружи катушки также складывается из магнитных полей отдельных витков, однако магнитные силовые линии располагаются не так густо, вследствие чего интенсивность магнитного поля там не столь велика, как внутри катушки.

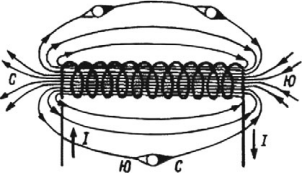
Магнитное поле катушки с током имеет такую же форму, как и поле прямолинейного постоянного магнита: силовые магнитные линии выходят из одного конца катушки и входят в другой ее конец. Поэтому катушка с током представляет собой искусственный электрический магнит. Обычно для усиления магнитного поля внутрь катушки вставляют стальной сердечник; такую катушку называют электромагнитом.

Направление линий магнитной индукции катушки с током находят по правилу правой руки:

если мысленно обхватить катушку с током ладонью правой руки так, чтобы четыре пальца указывали направление тока в ее витках, тогда большой палец укажет направление вектора магнитной индукции.

Для определения направления линий магнитного поля, создаваемого витком или катушкой, можно использовать также правило буравчика:

если вращать ручку буравчика по направлению тока в витке или катушке, то поступательное движение буравчика укажет направление вектора магнитной индукции.

Электромагниты нашли чрезвычайно широкое применение в технике. Полярность электромагнита (направление магнитного поля) можно определить и с помощью правила правой руки.

Видео:Парфенов К.В. - Олимпиадная физика для 11-го класса - 9. Движение зарядов в магнитном полеСкачать

Сила Ампера

Сила Ампера – сила, которая действует на проводник с током, находящийся в магнитном поле.

Закон Ампера: на проводник c током силой ​ ( I ) ​ длиной ​ ( l ) ​, помещенный в магнитное поле с индукцией ​ ( vec ) ​, действует сила, модуль которой равен:

где ​ ( alpha ) ​ – угол между проводником с током и вектором магнитной индукции ​ ( vec ) ​.

Направление силы Ампера определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции ​ ( B_perp ) ​ входила в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец покажет направление силы Ампера.

Сила Ампера не является центральной. Она направлена перпендикулярно линиям магнитной индукции.

Сила Ампера широко используется. В технических устройствах создают магнитное поле с помощью проводников, по которым течет электрический ток. Электромагниты используют в электромеханическом реле для дистанционного выключения электрических цепей, магнитном подъемном кране, жестком диске компьютера, записывающей головке видеомагнитофона, в кинескопе телевизора, мониторе компьютера. В быту, на транспорте и в промышленности широко применяют электрические двигатели. Взаимодействие электромагнита с полем постоянного магнита позволило создать электроизмерительные приборы (амперметр, вольтметр).

Простейшей моделью электродвигателя служит рамка с током, помещенная в магнитное поле постоянного магнита. В реальных электродвигателях вместо постоянных магнитов используют электромагниты, вместо рамки – обмотки с большим числом витков провода.

Коэффициент полезного действия электродвигателя:

где ​ ( N ) ​ – механическая мощность, развиваемая двигателем.

Коэффициент полезного действия электродвигателя очень высок.

Алгоритм решения задач о действии магнитного поля на проводники с током:

• сделать схематический чертеж, на котором указать проводник или контур с током и направление силовых линий поля;
• отметить углы между направлением поля и отдельными элементами контура;
• используя правило левой руки, определить направление силы Ампера, действующей на проводник с током или на каждый элемент контура, и показать эти силы на чертеже;
• указать все остальные силы, действующие на проводник или контур;
• записать формулы для остальных сил, упоминаемых в задаче. Выразить силы через величины, от которых они зависят. Если проводник находится в равновесии, то необходимо записать условие его равновесия (равенство нулю суммы сил и моментов сил);
• записать второй закон Ньютона в векторном виде и в проекциях;
• решить полученную систему уравнений относительно неизвестной величины;
• решение проверить.

Видео:Движение заряженных частиц Лекция 9-2Скачать

Сила Лоренца

Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.

Формула для нахождения силы Лоренца:

где ​ ( q ) ​ – заряд частицы, ​ ( v ) ​ – скорость частицы, ​ ( B ) ​ – модуль вектора магнитной индукции, ​ ( alpha ) ​ – угол между вектором скорости частицы и вектором магнитной индукции.

Направление силы Лоренца определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции ​ ( B_perp ) ​ входила в ладонь, а четыре вытянутых пальца указывали направление скорости положительно заряженной частицы, то отогнутый на 90° большой палец покажет направление силы Лоренца.

Если заряд частицы отрицательный, то направление силы изменяется на противоположное.

Важно!
Если вектор скорости сонаправлен с вектором магнитной индукции, то частица движется равномерно и прямолинейно.

В однородном магнитном поле сила Лоренца искривляет траекторию движения частицы.

Если вектор скорости перпендикулярен вектору магнитной индукции, то частица движется по окружности, радиус которой равен:

где ​ ( m ) ​ – масса частицы, ​ ( v ) ​ – скорость частицы, ​ ( B ) ​ – модуль вектора магнитной индукции, ​ ( q ) ​ – заряд частицы.

В этом случае сила Лоренца играет роль центростремительной и ее работа равна нулю. Период (частота) обращения частицы не зависит от радиуса окружности и скорости частицы. Формула для вычисления периода обращения частицы:

Угловая скорость движения заряженной частицы:

Важно!
Сила Лоренца не меняет кинетическую энергию частицы и модуль ее скорости. Под действием силы Лоренца изменяется направление скорости частицы.

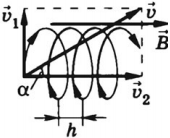
Если вектор скорости направлен под углом ​ ( alpha ) ​ (0° ( alpha ) ( vec_2 ) ​, параллелен вектору ( vec ) , а другой, ( vec_1 ) , – перпендикулярен ему. Вектор ( vec_1 ) не меняется ни по модулю, ни по направлению. Вектор ( vec_2 ) меняется по направлению. Сила Лоренца будет сообщать движущейся частице ускорение, перпендикулярное вектору скорости ( vec_1 ) . Частица будет двигаться по окружности. Период обращения частицы по окружности – ​ ( T ) ​.

Таким образом, на равномерное движение вдоль линии индукции будет накладываться движение по окружности в плоскости, перпендикулярной вектору ( vec ) . Частица движется по винтовой линии с шагом ​ ( h=v_2T ) ​.

Важно!
Если частица движется в электрическом и магнитном полях, то полная сила Лоренца равна:

Особенности движения заряженной частицы в магнитном поле используются в масс-спектрометрах – устройствах для измерения масс заряженных частиц; ускорителях частиц; для термоизоляции плазмы в установках «Токамак».

Алгоритм решения задач о действии магнитного (и электрического) поля на заряженные частицы:

• сделать чертеж, указать на нем силовые линии магнитного (и электрического) поля, нарисовать вектор начальной скорости частицы и отметить знак ее заряда;
• изобразить силы, действующие на заряженную частицу;
• определить вид траектории частицы;
• разложить силы, действующие на заряженную частицу, вдоль направления магнитного поля и по направлению, ему перпендикулярному;
• составить основное уравнение динамики материальной точки по каждому из направлений разложения сил;
• выразить силы через величины, от которых они зависят;
• решить полученную систему уравнений относительно неизвестной величины;
• решение проверить.

Видео:ОЛИМПИАДНАЯ ФИЗИКА. Магнитное поле - 1Скачать

Радиус окружности и период обращения частицы по окружности

Видео:ЕГЭ по физике 2016. задание 18. Частица в магнитном поле.Скачать

Движение заряженной частицы в магнитном поле.

Для вывода общих закономерностей движения заряженной частицы в магнитном поле будем считать магнитное поле однородным, электрические поля на частицу не действуют. При этом учтем очевидное:

а) Если заряженная частица движется в магнитном поле вдоль силовой линии, сила Лоренца, действующая на неё, равна нулю

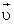
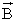
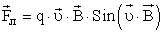
б) Если заряженная частица движется в магнитном поле со скоростью , перпендикулярно к вектору , то сила Лоренца, равная постоянна по модулю и перпендикулярна к траектории частицы.

Согласно второму закону Ньютона, эта сила создаёт центростремительное ускорение. Поэтому частица будет двигаться по окружности, радиус которой определяется из условия:

, , ,

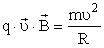
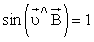
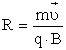
период вращения частицы, т. е. время, затрачиваемое ею на один полный оборот,

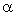
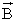
в) Если скорость заряженной частицы направлена под углом к вектору то её движение можно представить в виде двух движений: 1) равномерного прямолинейного движения вдоль поля, 2) равномерного движения по окружности в плоскости перпендикулярной полю (Рис. 23).

В результате этих двух движений возникает движение по винтовой линии, ось которой параллельна вектору 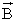. Шаг винтовой линии:

Направление, в котором закручивается частица, зависит от знака её заряда.

Действие магнитного поля на движущиеся заряженные частицы. Действие магнитного поля на проводник с током означает, что магнитное поле действует на движущиеся электрические заряды. Найдем силу, действующую на электрический заряд q при его движении в однородном магнитном поле с индукцией .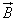
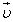
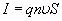
Сила тока I в проводнике связана с концентрацией n свободных заряженных частиц, скоростью их упорядоченного движения и площадью S поперечного сечения проводника следующим выражением:

,(1)

где q — заряд отдельной частицы.

.

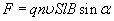
Так как произведение nSl равно числу свободных заряженных частиц в проводнике длиной l

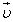
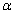
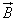
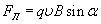
то сила, действующая со стороны магнитного поля на одну заряженную частицу, движущуюся со скоростью под углом к вектору индукции, равна

.(2)

Эту силу называют силой Лоренца.
Направление вектора силы Лоренца 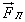определяется правилом левой руки, в нем за направление тока нужно брать направление вектора скорости положительного заряда (рис. 186). Для случая движения отрицательно заряженных частиц четыре пальца следует располагать противоположно направлению вектора скорости.

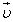
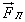
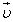
Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила , постоянная по модулю и направленная перпендикулярно вектору скорости (рис. 187).

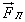
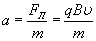
В вакууме под действием силы Лоренца частица приобретает центростремительное ускорение

(3)

и движется по окружности. Радиус r окружности, по которой движется частица, определяется из условия

, .(4)

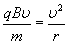
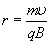
Период обращения частицы в однородном магнитном поле равен

.(5)

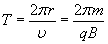
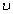
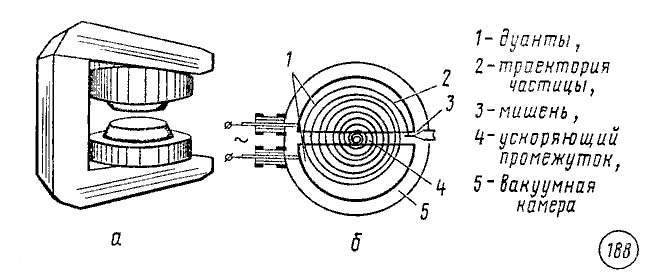
Последнее выражение показывает, что период обращения частицы в однородном магнитном поле при постоянной массе не зависит от скорости и радиуса r траектории ее движения. Этот факт используется, например, в ускорителе заряженных частиц — циклотроне.

Циклотрон. В этом ускорителе заряженные частицы — протоны, ядра атомов гелия — разгоняются переменным электрическим полем постоянной частоты в вакууме в зазоре между двумя металлическими электродами — дуантами. Дуанты находятся между полюсами постоянного электромагнита (рис. 188, а).

Под действием магнитного поля внутри дуантов заряженные частицы движутся по окружности. К моменту времени, когда они совершают половину оборота и подходят к зазору между дуантами, направление вектора напряженности электрического поля между дуантами изменяется на противоположное и частицы вновь испытывают ускорение. Каждую следующую половину оборота частицы пролетают по окружности все большего радиуса (рис. 188, б), но период их обращения остается неизменным. Поэтому для ускорения частиц на дуанты подается переменное напряжение с постоянным периодом.
Ускорение частиц в циклотроне с постоянным периодом возможно лишь до значений скоростей, значительно меньших скорости света. С приближением скорости частицы к скорости света в вакууме, равной c = 300000 км/с, масса частицы возрастает, вследствие чего увеличивается период ее обращения в магнитном поле. Равенство периода обращения частицы и периода изменения электрического поля нарушается, ускорение прекращается.

топлива по сравнению с обычной тепловой электростанцией.

В заключение, по традиции, предлагаем Вашему вниманию шпаргалку по этой теме:

Видео:Урок 90. Движение по окружности (ч.2)Скачать

I. Механика

Видео:сила Лоренца | правило левой руки | физика 11 классСкачать

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Радиус окружности и период обращения частицы по окружности

α-частица, кинетическая энергия которой W=500 эВ, влетает в однородное магнитное поле, перпендикулярное к направлению ее движения. Индукция магнитного поля B=0,1 Тл. Найти силу F, действующую на α-частицу, радиус R окружности, по которой движется α-частица, и период обращения Т α-частицы.

Дано:

W=500 эВ = 800·10 -19 Дж

Решение:

На α-частицу, движущуюся в магнитном поле, действует сила Лоренца

Силовая линия вектора В перпендикулярна скорости, т.е.

Скорость найдем, зная кинетическую энергию α-частицы

ила Лоренца является центростремительной

Радиус R окружности, по которой движется α-частица, будет равен