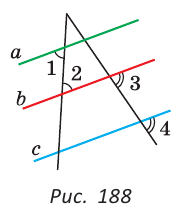
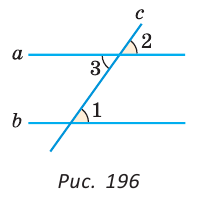
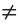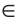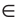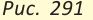Угол 3 = 180-130=60 крадуов
угол абц= 130
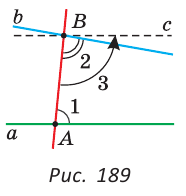
угол абд=130/2=65, значит угол 2=65, а угол 1 = 180-65= 115
- Как написать хороший ответ?
- Параллельные прямые — определение и вычисление с примерами решения
- Определения параллельных прямых
- Признаки параллельности двух прямых
- Аксиома параллельных прямых
- Обратные теоремы
- Пример №1
- Параллельность прямых на плоскости
- Две прямые, перпендикулярные третьей
- Накрест лежащие, соответственные и односторонние углы
- Признаки параллельности прямых
- Пример №2
- Пример №3
- Пример №4
- Аксиома параллельных прямых
- Пример №5
- Пример №6
- Свойства параллельных прямых
- Пример №7
- Пример №8
- Углы с соответственно параллельными и соответственно перпендикулярными сторонами
- Расстояние между параллельными прямыми
- Пример №9
- Пример №10
- Справочный материал по параллельным прямым
- Перпендикулярные и параллельные прямые
- Прямые а и б параллельны bd биссектриса
- 🎬 Видео
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:№202. На рисунке 116 прямые а, b и с пересечены прямой d, ∠1=42°, ∠2=140°, ∠3=138°. Какие из прямыхСкачать
Параллельные прямые — определение и вычисление с примерами решения
Содержание:
Параллельные прямые:
Ранее мы уже дали определение параллельных прямых.
Напомним, что две прямые на плоскости называются параллельными, если они не пересекаются.
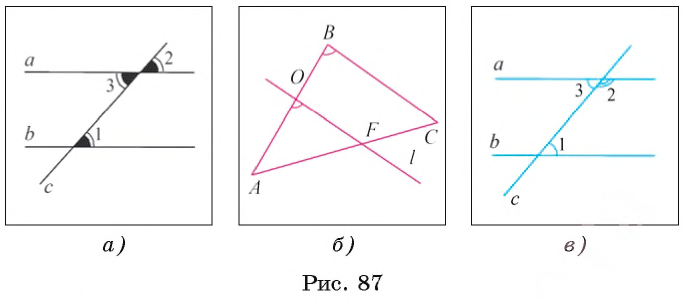
Например, если две прямые a и b плоскости перпендикулярны прямой c этой плоскости, то они не пересекаются, т. е. параллельны (рис. 85, а). Этот факт нами был доказан как следствие из теоремы о существовании и единственности перпендикуляра, проведенного из точки к данной прямой.
Два отрезка называются параллельными, если они лежат на параллельных прямых.
Отрезок называется параллельным прямой, если он лежит на прямой, параллельной данной прямой.
Например, на рисунке 85, B изображены параллельные отрезки АВ и СD (параллельность отрезков АВ и СD обозначается следующим образом: АВ 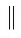
Аналогично определяется параллельность двух лучей, отрезка и прямой, луча и прямой, а также отрезка и луча. Например, на рисунке 85, в изображены отрезок PQ, параллельный прямой l, и отрезок ТК, параллельный лучу СD.
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Определения параллельных прямых
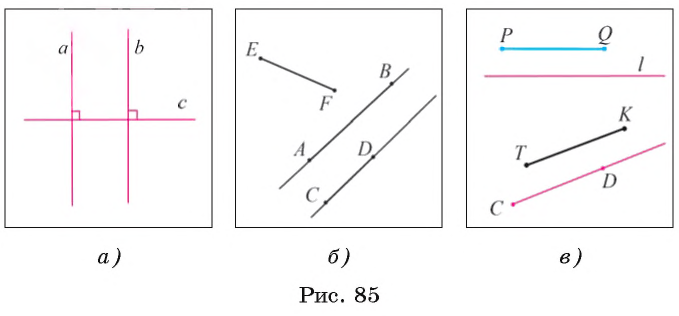
На рисунке 10 прямые 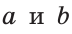
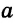
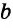
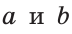
Это можно записать так: 

На плоскости две прямые могут либо пересекаться, либо не пересекаться. Прямые на плоскости, которые не пересекаются, называются параллельными. Если прямые 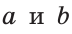
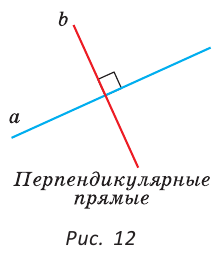
Две прямые, которые при пересечении образуют прямой угол, называются перпендикулярными прямыми. Если прямые 
ВАЖНО!
Совпадающие прямые будем считать одной прямой. Поэтому, если сказано «даны две прямые», это означает, что даны две различные несовпадающие прямые. Это касается также точек, лучей, отрезков и других фигур.
Есть два способа практического сравнения длин отрезков, а также величин углов: 1) наложение; 2) сравнение результатов измерения. Оба способа являются приближенными. В геометрии отрезки и углы могут быть равны, если это дано по условию либо следует из условия на основании логических рассуждений.
Признаки параллельности двух прямых
Прямая c называется секущей по отношению к прямым a и b, если она пересекает каждую из них в различных точках.
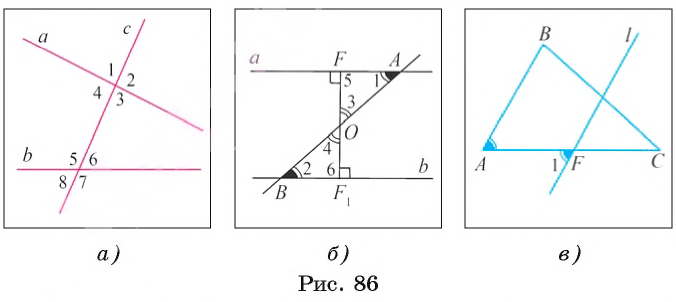
При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 86, а обозначены цифрами. Некоторые пары этих углов имеют специальное название:
- углы 3 и 5, 4 и 6 называются внутренними накрест лежащими;
- углы 4 и 5, 3 и 6 называются внутренними односторонними;
- углы 1 и 5, 4 и 8, 2 и 6, 3 и 7 называются соответственными.
Рассмотрим признаки параллельности двух прямых.
Теорема 1 (признак параллельности прямых по равенству внутренних накрест лежащих углов). Если при пересечении двух прямых секущей внутренние накрест лежащие углы равны, то прямые параллельны.
- Пусть при пересечении прямых а и b секущей АВ внутренние накрест лежащие углы 1 и 2 равны (рис. 86, б). Докажем, что а
b.
- Если
1 =
2 = 90°, то а
АВ и b
АВ. Отсюда в силу теоремы 1 (глава 3, § 2) следует, что а
b.
- Если
1 =
2
90°, то из середины О отрезка АВ проведем отрезок ОF
a.
- На прямой b отложим отрезок ВF1 = АF и проведем отрезок ОF1.
- Заметим, что
ОFА =
ОF1В по двум сторонам и углу между ними (АО = ВО, АF= BF1 и
1 =
2). Из равенства этих треугольников следует, что
З =
4 и
5 =
6.
- Так как
3 =
4, а точки А, В и О лежат на одной прямой, то точки F1, F и О также лежат на одной прямой.
- Из равенства
5 =
6 следует, что
6 = 90°. Получаем, что а
FF1 и b
FF1, а а
b.
Например, пусть прямая l проходит через точку F, принадлежащую стороне АС треугольника АВС, так, что 
Теорема 2 (признак параллельности прямых по равенству соответственных углов). Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
1) Пусть при пересечении прямых а и b секущей с соответственные углы равны, например 

2) Заметим, что 

3) Из равенств 





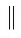
Например, пусть прямая l пересекает стороны AB и АС треугольника ABC в точках О и F соответственно и 

Теорема 3 (признак параллельности прямых по сумме градусных мер внутренних односторонних углов). Если, при пересечении двух прямых секущей сумма градусных мер внутренних односторонних углов равна 180°, то прямые параллельны.
- Пусть при пересечении двух прямых а и b секущей с сумма градусных мер внутренних односторонних углов равна 180°, например
1 +
2 = 180° (рис. 87, в).
- Заметим, что
3 +
2 = 180°, так как углы 3 и 2 являются смежными.
- Из равенств
l +
2 = 180° и
3 +
2 = 180° следует, что
1 =
3.
- Поскольку равны внутренние накрест лежащие углы 1 и 3, то прямые а и b параллельны.
Аксиома параллельных прямых
Как уже отмечалось, при доказательстве теорем опираются на уже доказанные теоремы и некоторые исходные утверждения, которые называются аксиомами. Познакомимся еще с одной аксиомой, имеющей важное значение для дальнейшего построения геометрии.
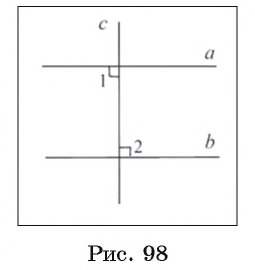
Пусть в плоскости дана прямая а и не лежащая на ней произвольная точка О. Можно доказать, что через точку О в этой плоскости проходит прямая, параллельная прямой а. Действительно, проведем через точку О прямую с, перпендикулярную прямой a, затем прямую b, перпендикулярную прямой с. Так как прямые а и b перпендикулярны прямой с, то они не пересекаются, т. е. параллельны (рис. 92). Следовательно, через точку O 
Большой вклад в решение этого вопроса внес русский математик Н. И. Лобачевский (1792—1856).
Таким образом, в качестве одной из аксиом принимается аксиома параллельных прямых, которая формулируется следующим образом.
Аксиома параллельных прямых. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Непосредственно из аксиомы параллельны х прямых в качестве следствий получаем следующие теоремы.
Теорема 1. Если две прямые параллельны третьей прямой, то они параллельны.
Пусть прямые а и b параллельны прямой с. Докажем, что а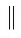
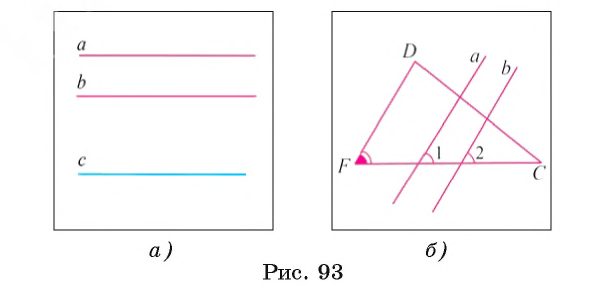
Например, пусть прямые а и b пересекают сторону FС треугольника FDС так, что 



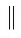
Теорема 2. Пусть три прямые лежат в плоскости. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.
Пусть прямые а и b параллельны, а прямая с пересекает прямую а в точке О (рис. 94, а). Докажем, что прямая с пересекает прямую b. Проведем доказательство методом от противного. Допустим, что прямая с не пересекает прямую b. Тогда через точку О проходят две прямые а и с, не пересекающие прямую b, т. е. параллельные ей (рис. 94, б). Но это противоречит аксиоме параллельных прямых. Следовательно, наше предположение неверно и прямая с пересекает прямую b.
Обратные теоремы
В формулировке любой теоремы можно выделить две ее части: условие и заключение. Условие теоремы — это то, что дано, а заключение — то, что требуется доказать. Например, рассмотрим признак параллельности прямых: если при пересечении двух прямых секущей внутренние накрест лежащие углы равны, то прямые параллельны. В этой теореме условием является первая часть утверждения: при пересечении двух прямых секущей внутренние накрест лежащие углы равны (это дано), а заключением — вторая часть: прямые параллельны (это требуется доказать).
Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением — условие данной теоремы.
Теперь докажем теоремы, обратные признакам параллельности прямых.
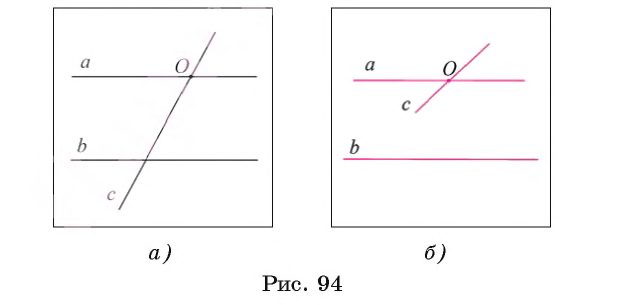
Теорема 3 (о равенстве внутренних накрест лежащих углов). Если две параллельные прямые пересечены секущей, то внутренние накрест лежащие углы равны.
1) Пусть параллельные прямые а и b пересечены секущей AВ (рис. 95, а). Докажем, что внутренние накрест лежащие углы, например 1 и 2, равны.
2) Доказательство теоремы проведем методом от противного. Допустим, что углы 1 и 2 не равны. Отложим угол QАВ, равный углу 2, так, чтобы угол QАВ и 
3) По построению накрест лежащие углы QАВ и 
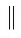


Например, пусть прямая l параллельна стороне ВС треугольника АВС (рис. 95, б). Тогда 

Теорема 4 (о равенстве соответственных углов). Если две параллельные прямые пересечены секущей, то соответственные углы равны.
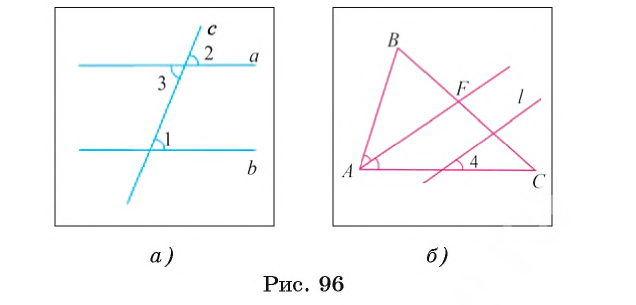
- Пусть параллельные прямые а и b пересечены секущей с. Докажем, что соответственные углы, например 1 и 2, равны (рис. 96, а).
- Так как прямые а и b параллельны, то по теореме 3 данного параграфа накрест лежащие углы 1 и 3 равны, т. е.
1 =
3. Кроме того,
2 =
3, так как они вертикальные.
- Из равенств
1 =
3 и
2 =
3 следует, что
1 =
2.
Например, пусть прямая l параллельна биссектрисе AF треугольника ABC (рис. 96, б), тогда 





Теорема 5 (о свойстве внутренних односторонних углов). Если две параллельные прямые пересечены секущей, то сумма градусных мер внутренних односторонних углов равна 180°.
1) Пусть параллельные прямые а и b пересечены секущей с. Докажем, например, что 

2) Так как прямые а и b параллельны, то по теореме 4 справедливо равенство 

3) Углы 2 и 3 смежные, следовательно, 

4) Из равенств 





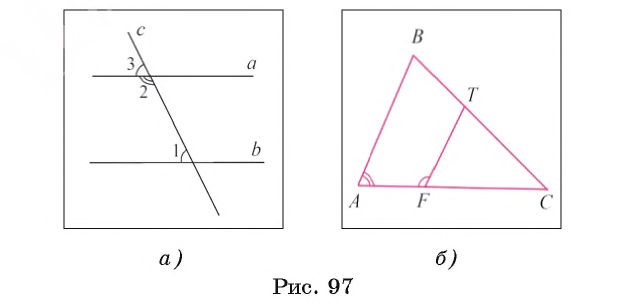
Например, пусть отрезок FT параллелен стороне АВ треугольника ABC (рис. 97, б). Тогда 

Заметим, если доказана какая-либо теорема, то отсюда еще не следует, что обратная теорема верна. Например, известно, что вертикальные углы равны, но если углы равны, то отсюда не вытекает, что они являются вертикальными.
Пример №1
Докажите, что если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой прямой.
1) Пусть прямые а и b параллельны и с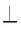
2) Так как прямая с пересекает прямую а, то она пересекает и прямую b.
3) При пересечении параллельных прямых а и b секущей с образуются равные внутренние накрест лежащие углы 1 и 2.
Так как 


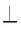
Что и требовалось доказать.
Видео:№186. На рисунке 106 прямые а и b пересечены прямой с. Докажите, что a||b, если: a)∠1=37°Скачать

Параллельность прямых на плоскости
Параллельность прямых — одно из основных понятий геометрии. Параллельность часто встречается в жизни. Посмотрев вокруг, можно убедиться, что мы живем в мире параллельных линий. Это края парты, столбы вдоль дороги, полоски «зебры» на пешеходном переходе.
Две прямые, перпендикулярные третьей
Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Лучи и отрезки называются параллельными, если они лежат на параллельных прямых. Если прямые 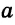
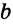
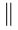
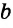
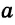
Вы уже знаете теорему о параллельных прямых на плоскости: «Две прямые, перпендикулярные третьей, параллельны между собой». Другими словами, если 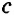
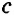
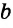
Данная теорема позволяет решить две важные практические задачи.
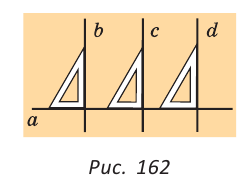
Первая задача заключается в проведении нескольких параллельных прямых.
Пусть дана прямая 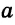
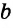
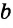
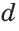
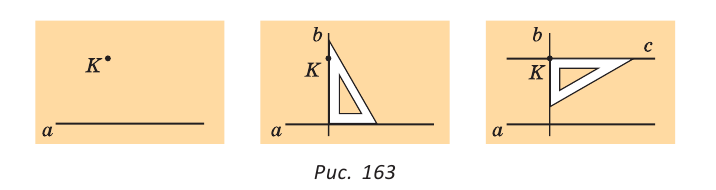
Вторая задача — проведение прямой, параллельной данной и проходящей через точку, не лежащую на данной прямой.
По рисунку 163 объясните процесс проведения прямой 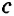
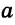
Из построения следует: так как 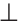
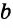
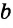
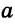
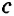
Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной.
Накрест лежащие, соответственные и односторонние углы
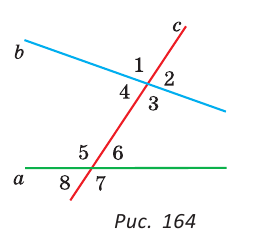
При пересечении двух прямых 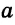
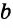
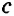
Некоторые пары этих углов имеют специальные названия:
3 и
5,
4 и
6 — внутренние накрест лежащие углы;
2 и
8,
1 и
7 — внешние накрест лежащие углы;
2 и
6,
3 и
7,
1 и
5,
4 и
8 — соответственные углы;
3 и
6,
4 и
5 — внутренние односторонние углы;
2 и
7,
1 и
8 — внешние односторонние углы.
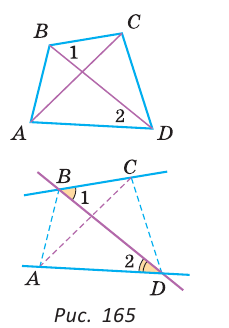
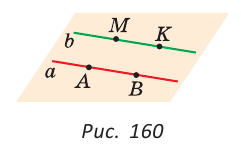
На рисунке 165 отмечены углы 1 и 2. Они являются внутренними накрест лежащими углами при прямых ВС и AD и секущей BD. В этом легко убедиться, продлив отрезки ВС, AD и BD.
Признаки параллельности прямых
С указанными парами углов связаны следующие признаки параллельности прямых.
Теорема (первый признак параллельности прямых). Если при пересечении двух прямых секущей внутренние накрест лежащие углы равны, то прямые параллельны.
Дано: 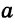
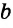
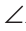
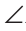
Доказать: 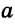
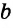
Доказательство:
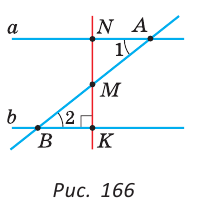
Из середины М отрезка АВ опустим перпендикуляр МК на прямую 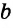
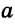
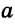
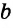
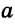
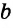
Теорема (второй признак параллельности прямых). Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Дано: 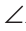
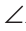
Доказать: 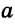
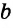
Доказательство:
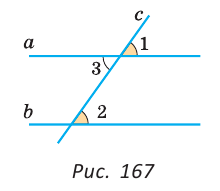
Углы 1 и 3 равны как вертикальные. А так как углы 1 и 2 равны по условию, то углы 2 и 3 равны между собой. Но углы 2 и 3 — внутренние накрест лежащие при прямых 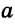
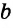
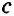
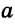
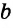
Теорема (третий признак параллельности прямых). Если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Дано: 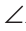
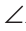
Доказать: 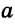
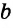
Доказательство:
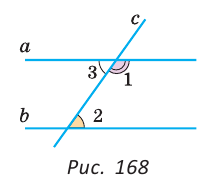
Углы 1 и 3 — смежные, поэтому их сумма равна 180°. А так как сумма углов 1 и 2 равна 180° по условию, то углы 2 и 3 равны между собой. Но углы 2 и 3 — внутренние накрест лежащие при прямых 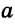
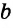
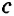
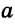
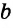
Пример №2
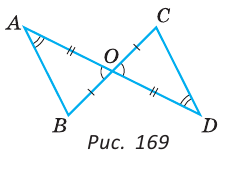
Доказать, что если отрезки AD и ВС пересекаются и точкой пересечения делятся пополам, то прямые АВ и CD параллельны.
Доказательство:
Пусть О — точка пересечения отрезков AD и ВС (рис. 169).
Треугольники АОВ и DOC равны по двум сторонам и углу между ними (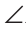
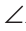
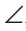
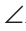
Пример №3
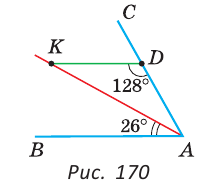
На биссектрисе угла ВАС взята точка К, а на стороне АС — точка D, 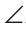
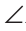
Доказательство:
Так как АК — биссектриса угла ВАС (рис. 170), то
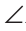
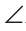
Углы ADK и ВАС — внутренние односторонние при прямых KD и ВА и секущей АС. А поскольку 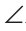
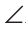
Пример №4
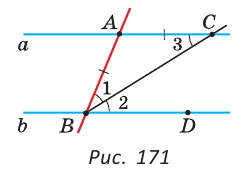
Биссектриса ВС угла ABD отсекает на прямой а отрезок АС, равный отрезку АВ. Доказать, что прямые а и b параллельны (рис. 171).
Доказательство:
Так как ВС — биссектриса угла ABD, то 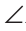
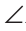

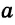
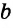
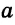
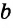
Реальная геометрия
На рисунке 184 изображен электронный угломер — инструмент для нанесения параллельных линий на рейке или доске. Прибор состоит из двух частей, скрепленных винтом. Одна часть неподвижная, она прижимается к доске, а другая поворачивается на необходимый угол, градусная мера которого отражается на экране угломера. Зажав винт, закрепляют нужный угол. Сдвинув неподвижную часть угломера вдоль доски, наносят новую линию разметки. Так получают параллельные линии, по которым затем распиливают доску.
Аксиома параллельных прямых
Вы уже знаете, что на плоскости через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной (см. § 15). Из пятого постулата Евклида (постулат — аксиоматическое предположение) следует, что такая прямая — единственная.
На протяжении двух тысячелетий вокруг утверждения о единственности параллельной прямой разыгрывалась захватывающая и драматичная история! Со времен Древней Греции математики спорили о том, можно доказать пятый постулат Евклида или нет. То есть это теорема или аксиома?
В конце концов работы русского математика Н. И. Лобачевского (1792—1856) позволили выяснить, что доказать пятый постулат нельзя. Поэтому это утверждение является аксиомой.
Аксиома параллельных прямых. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.
Если прямая 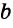
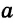
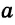
Поиски доказательства пятого постулата Евклида привели к развитию математики и физики, к пересмотру научных представлений о геометрии Вселенной. Решая проблему пятого постулата, Лобачевский создал новую геометрию, с новыми аксиомами, теоремами, отличающуюся от геометрии Евклида, которая теперь так и называется — геометрия Лобачевского.
Вы уже знаете, что на плоскости две прямые, перпендикулярные третьей, параллельны между собой. А если две прямые параллельны третьей прямой, то что можно сказать про первые две прямые? На этот вопрос отвечает следующая теорема.
Теорема (о двух прямых, параллельных третьей). На плоскости две прямые, параллельные третьей, параллельны между собой.
Дано: 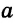
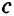
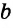
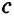
Доказать: 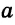
Доказательство:
Предположим, что прямые 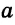
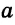
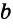
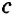
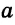
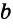
Метод доказательства «от противного»
При доказательстве теоремы о двух прямых, параллельных третьей, мы применили метод доказательства от противного (то есть «от противоположного»). Суть его в следующем. Утверждение любой теоремы делится на условие — то, что в теореме дано, и заключение — то, что нужно доказать.
В доказанной выше теореме условие: «Каждая из двух прямых параллельна третьей прямой», а заключение: «Эти две прямые параллельны между собой».
Используя метод от противного, предполагают, что из данного условия теоремы следует утверждение, противоположное (противное) заключению теоремы. Если при сделанном предположении путем логических рассуждений приходят к какому-либо утверждению, противоречащему аксиомам или ранее доказанным теоремам, то сделанное предположение считается неверным, а верным — ему противоположное.
В доказательстве нашей теоремы мы предположили, что эти две прямые не параллельны, а пересекаются в точке. И пришли к выводу, что тогда нарушается аксиома параллельных прямых. Следовательно, наше предположение о пересечении прямых не верно, а верно ему противоположное: прямые не пересекаются, то есть параллельны.
Методом от противного ранее была доказана теорема о двух прямых, перпендикулярных третьей.
Данный метод является очень мощным логическим инструментом доказательства. Причем не только в геометрии, но и в любом аргументированном споре.
Теорема. Если на плоскости прямая пересекает одну из двух параллельных прямых, то она пересекает и другую прямую.
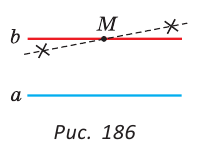
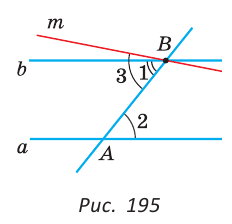
Пример №5
На рисунке 188 
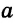
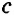
Доказательство:
Так как накрест лежащие углы 1 и 2 равны, то 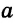
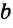
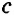
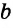
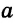
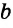
Пример №6
Доказать, что если сумма внутренних односторонних углов при двух данных прямых и секущей меньше 180°, то эти прямые пересекаются.
Доказательство:
Пусть 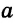
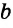
Отложим от луча АВ угол 3, который в сумме с углом 1 дает 180°. Получим прямую 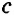
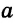
Свойства параллельных прямых
Вы знаете, что если две прямые пересечены секущей и накрест лежащие углы равны, то прямые параллельны. Это признак параллельности прямых. Обратное утверждение звучит так: «Если две прямые параллельны и пересечены секущей, то накрест лежащие углы равны». Это утверждение верно, и оно выражает свойство параллельных прямых. Докажем его и два других свойства для соответственных и односторонних углов.
Теорема (о свойстве накрест лежащих углов при параллельных прямых и секущей). Если две параллельные прямые пересечены секущей, то внутренние накрест лежащие углы равны.
Дано: 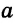
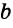
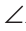
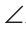
Доказать: 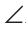
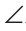
Доказательство:
Предположим, что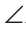
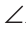
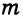
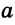
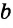
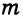
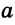
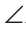
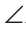
Теорема (о свойстве соответственных углов при параллельных прямых и секущей). Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Дано: 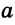
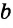
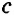
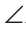
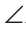
Доказать: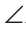
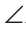
Доказательство:
Углы 1 и 3 равны как накрест лежащие при параллельных прямых 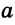
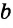
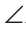
Теорема (о свойстве односторонних углов при параллельных прямых и секущей).
Если две параллельные прямые пересечены секущей, то сумма внутренних односторонних углов равна 180°.
Дано: 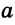
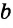
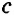
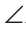
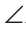
Доказать: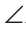
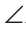
Доказательство:
Углы 2 и 3 — смежные. По свойству смежных углов 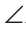
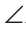
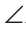
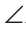
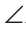
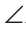
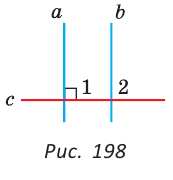
Следствие.
Прямая, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой прямой.
На рисунке 198 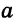
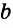
Доказанные нами теоремы о свойствах углов при двух параллельных прямых и секущей являются обратными признакам параллельности прямых.
Чтобы не путать признаки и свойства параллельных прямых, нужно помнить следующее:
- а) если ссылаются на признак параллельности прямых, то требуется доказать параллельность некоторых прямых;
- б) если ссылаются на свойство параллельных прямых, то параллельные прямые даны, и нужно воспользоваться каким-то их свойством.
Пример №7
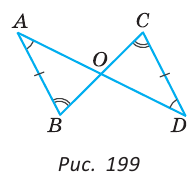
Доказать, что если отрезки АВ и CD равны и параллельны, а отрезки AD и ВС пересекаются в точке О, то треугольники АОВ и DOC равны.
Доказательство:
Углы BAD и CD А равны как накрест лежащие при параллельных прямых АВ и CD и секущей AD (рис. 199).
Углы ABC и DCB равны как накрест лежащие при параллельных прямых АВ и CD и секущей ВС. Тогда 

Пример №8
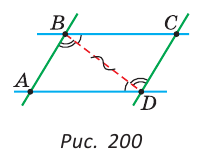
Доказать, что отрезки параллельных прямых, заключенные между двумя другими пересекающими их параллельными прямыми, равны между собой.
Доказательство:
Пусть АВ || CD, ВС || AD (рис. 200).
Докажем, что АВ = CD, ВС=AD. Проведем отрезок BD. У треугольников ABD и CDB сторона BD — общая,
Геометрия 3D
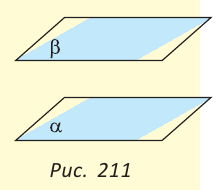
Две плоскости называются параллельными, если они не имеют общих точек (не пересекаются).
Если плоскости 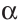
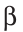
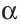
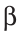
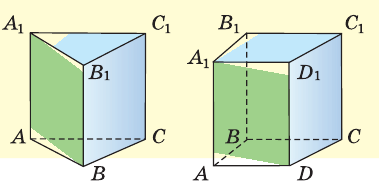
Существует еще один вид многогранников — призмы (рис. 212). У призмы две грани (основания) — равные многоугольники, которые лежат в параллельных плоскостях, а остальные грани (боковые) — параллелограммы (задача 137).
У прямой призмы боковые грани — прямоугольники, боковые ребра перпендикулярны плоскостям оснований и равны между собой. На рисунке 212 изображены треугольная и четырехугольная прямые призмы. У них параллельны плоскости верхней и нижней граней.
Углы с соответственно параллельными и соответственно перпендикулярными сторонами
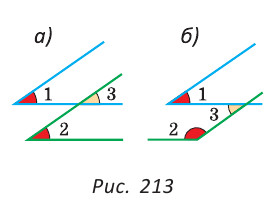
Теорема (об углах с соответственно параллельными сторонами).
Углы с соответственно параллельными сторонами или равны (если оба острые или оба тупые), или в сумме составляют 180° (если один острый, а другой тупой).
1) Острые углы 1 и 2 (рис. 213, а) — это углы с соответственно параллельными сторонами. Используя рисунок, докажите самостоятельно, что углы 1 и 2 равны.
2) Острый угол 1 и тупой угол 2 (рис. 213, б) — это углы с соответственно параллельными сторонами. Используя этот рисунок и результат пункта 1), докажите, что сумма углов 1 и 2 равна 180°.
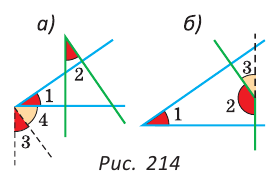
Теорема (об углах с соответственно перпендикулярными сторонами).
Углы с соответственно перпендикулярными сторонами или равны (если оба острые или оба тупые), или в сумме составляют 180° (если один острый, а другой тупой).
Доказательство:
1) Острые углы 1 и 2 — это углы с соответственно перпендикулярными сторонами (рис. 214, а). Построим острый угол 3 в вершине угла 1, стороны которого параллельны сторонам угла 2. Стороны угла 3 перпендикулярны сторонам угла 1 (прямая, перпендикулярная одной из параллельных прямых, перпендикулярна и другой прямой). По предыдущей теореме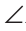
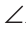
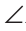
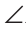
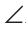
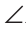
2) Острый угол 1 и тупой угол 2 — это углы с соответственно перпендикулярными сторонами (рис. 214, б). Используя этот рисунок и результат пункта 1), докажите самостоятельно, что сумма углов 1 и 2 равна 180°.
Запомнить:
- Признаки параллельности прямых: «Если при пересечении двух прямых секущей накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180°, то прямые параллельны».
- Свойства параллельных прямых: «Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны, соответственные углы равны и сумма односторонних углов равна 180°».
- На плоскости две прямые, перпендикулярные третьей, параллельны между собой.
- На плоскости две прямые, параллельные третьей, параллельны между собой.
- Прямая, перпендикулярная одной из двух параллельных прямых, будет перпендикулярна и другой прямой.
- Углы с соответственно параллельными сторонами или равны, или в сумме составляют 180°.
- Углы с соответственно перпендикулярными сторонами или равны, или в сумме составляют 180°.
Расстояние между параллельными прямыми
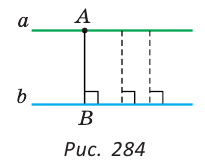
Определение. Расстоянием между параллельными прямыми называется расстояние от точки одной из этих прямых до другой прямой.
Если 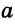
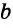
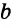
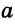
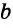
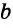
Теорема (о расстоянии между параллельными прямыми).
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Дано: 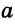
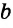
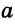
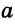
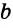
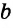
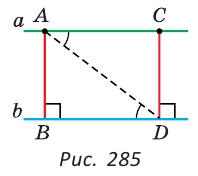
Доказать: АВ = CD (рис. 285).
Доказательство:
Проведем отрезок AD. Углы CAD и BDA равны как внутренние накрест лежащие при параллельных прямых 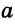
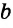
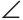
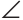
Следствие.
Все точки, лежащие в одной полуплоскости относительно данной прямой и равноудаленные от этой прямой, лежат на прямой, параллельной данной.
Доказательство:
Пусть перпендикуляры АВ и CD к прямой 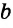
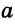
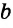
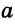
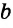
В силу того что прямая, перпендикулярная к одной из двух параллельных прямых, будет перпендикулярна и к другой прямой, перпендикуляр АВ к прямой 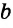
Пример №9
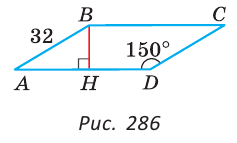
В четырехугольнике ABCD АВ || CD, AD || ВС, АВ = 32 см, 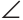
Решение:
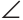
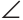
Тогда 
Расстояние между параллельными прямыми измеряется длиной перпендикуляра, опущенного из любой точки одной из прямых на другую прямую. Опустим перпендикуляр ВН на прямую AD. В прямоугольном треугольнике АВН катет ВН лежит против угла в 30°. Поэтому он равен половине гипотенузы. Значит, ВН =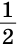
Пример №10
Найти геометрическое место точек, равноудаленных от двух данных параллельных прямых.
Решение:
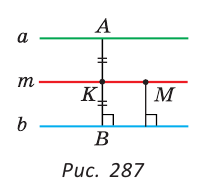
1) Пусть 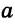
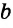
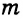
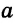
Тогда 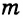
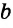
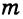
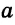
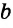
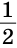
2) Пусть некоторая точка М (см. рис. 287) равноудалена от прямых 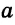
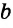
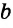
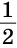
Таким образом, все точки прямой 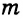
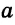
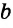
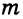
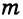
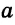
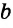
Геометрия 3D
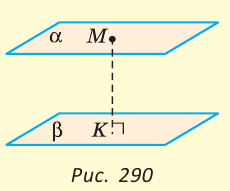
Расстоянием между параллельными плоскостями называется длина перпендикуляра, опущенного из точки, принадлежащей одной из плоскостей, на другую плоскость (рис. 290). В вашем классе пол и потолок — части параллельных плоскостей. Расстояние между ними равно высоте классной комнаты.
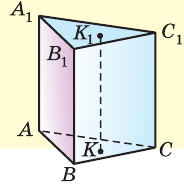
Высотой прямой призмы называется расстояние между плоскостями оснований. Отрезок КК1 — перпендикуляр к плоскости ABC, равный ее высоте. У прямой призмы боковые ребра перпендикулярны плоскостям оснований. Поэтому высота призмы равна длине бокового ребра, то есть АА1 = КК1 (рис. 291).
Запомнить:
- Сумма углов треугольника равна 180°.
- Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
- Катет меньше гипотенузы. Перпендикуляр меньше наклонной, проведенной из той же точки к одной прямой.
- Прямоугольные треугольники могут быть равны: 1) по двум катетам; 2) по катету и прилежащему острому углу; 3) по катету и противолежащему острому углу; 4) по гипотенузе и острому углу; 5) по катету и гипотенузе.
- Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. Если катет равен половине гипотенузы, то он лежит против угла в 30°.
- В треугольнике против большей стороны лежит больший угол, а против большего угла — большая сторона.
- В треугольнике любая сторона меньше суммы двух других его сторон (неравенство треугольника).
- Любая точка биссектрисы равноудалена от сторон угла. Если точка внутри угла равноудалена от сторон угла, то она лежит на биссектрисе этого угла.
- Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Если в треугольнике медиана равна половине стороны, к которой она проведена, то треугольник прямоугольный.
- Биссектрисы треугольника пересекаются в одной точке (2-я замечательная точка).
- Расстояние от любой точки одной из параллельных прямых до другой прямой есть величина постоянная.
Справочный материал по параллельным прямым
Параллельные прямые
- ✓ Две прямые называют параллельными, если они не пересекаются.
- ✓ Основное свойство параллельных прямых (аксиома параллельности прямых). Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
- ✓ Две прямые, перпендикулярные третьей прямой, параллельны.
- ✓ Если две прямые параллельны третьей прямой, то они параллельны.
- ✓ Расстоянием между двумя параллельными прямыми называют расстояние от любой точки одной из прямых до другой прямой.
Признаки параллельности двух прямых
- ✓ Если две прямые а и b пересечь третьей прямой с, то образуется восемь углов (рис. 246). Прямую с называют секущей прямых а и b.
- Углы 3 и 6, 4 и 5 называют односторонними.
- Углы 3 и 5, 4 и 6 называют накрест лежащими.
- Углы 6 и 2, 5 и 1, 3 и 7, 4и 8 называют соответственными.
- ✓ Если накрест лежащие углы, образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны.
- ✓ Если сумма односторонних углов, образующихся при пересечении двух прямых секущей, равна 180°, то прямые параллельны.
- ✓ Если соответственные углы, образующиеся при пересечении двух прямых секущей, равны, то прямые параллельны.
Свойства параллельных прямых
- ✓ Если две параллельные прямые пересекаются секущей, то:
- • углы, образующие пару накрест лежащих углов, равны;
- • углы, образующие пару соответственных углов, равны;
- • сумма углов, образующих пару односторонних углов, равна 180°.
- ✓ Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Перпендикулярные и параллельные прямые
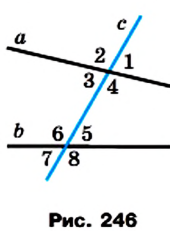
Две прямые называют взаимно перпендикулярными, если они пересекаются под прямым углом.
На рисунке 264 прямые 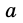
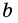
На рисунке 265 прямые 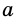
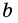
Основное свойство параллельных прямых (аксиома параллельности прямых). Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.
Углы, образованные при пересечении двух прямых секущей. Признаки и свойство параллельности прямых. Свойства углов, образованных при пересечении двух параллельных прямых секущей
Прямую с называют секущей для прямых 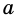
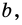
Пары углов 4 и 5; 3 и 6 называют внутренними односторонними; пары углов 4 и 6; 3 и 5 — внутренними накрест лежащими; пары углов 1 и 5; 2 и 6; 3 и 7; 4 и 8 — соответственными углами.
Признаки параллельности прямых:
- Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
- Если при пересечении двух прямых секущей внутренние накрест лежащие углы равны, то прямые параллельны.
- Если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
- Две прямые, перпендикулярные третьей, параллельны.
Свойство параллельных прямых. Две прямые, параллельные третьей прямой, параллельны друг другу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Соотношения между сторонами и углами треугольника
- Неравенство треугольника — определение и вычисление
- Свойства прямоугольного треугольника
- Расстояние между параллельными прямыми
- Медианы, высоты и биссектрисы треугольника
- Равнобедренный треугольник и его свойства
- Серединный перпендикуляр к отрезку
- Второй и третий признаки равенства треугольников
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:№536. Отрезок BD является биссектрисой треугольника ABC. а) Найдите АВ, если ВС = 9 смСкачать

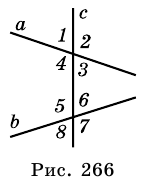
Прямые а и б параллельны bd биссектриса
305. Параллельны ли изображённые на рисунке 212 прямые a и b , если:
3) ∠ 4 = 125°, ∠ 6 = 55°;
4) ∠ 2 = 35°, ∠ 5 = 146°;
5) ∠ 1 = 98°, ∠ 6 = 82°;
6) ∠ 1 = 143°, ∠ 7 = 37°?
306. На каких из рисунков 213, а – г прямые m и n параллельны?
307. На рисунке 214 укажите все пары параллельных прямых.
308. На рисунке 215 укажите параллельные прямые, если ∠ 1 = 53°, ∠ 2 = 128°, ∠ 3 = 127°.
309. На рисунке 216 AB = BC , CD = DK . Докажите, что AB ‖ DK .
310. На рисунке 217 AK — биссектриса угла BAC , AM = MK . Докажите, что MK ‖ AC .
311. На рисунке 218 ∠ ACB = ∠ ACD , AD = CD . Докажите, что BC ‖ AD .
312. В треугольнике ABC известно, что AB = BC , ∠ A = 60°, ∠ BCD — смежный с ∠ ACB , CM — биссектриса угла BCD . Докажите, что AB ‖ CM .
313. Отрезки AB и CD пересекаются в точке O и делятся этой точкой пополам. Докажите, что AC ‖ BD .
314. На рисунке 219 AB = CD , BC = AD . Докажите, что AB ‖ CD .
315. Известно, что некоторая прямая m пересекает прямую a (рис. 220). Пересекает ли прямая m прямую b ?
316. Каково взаимное расположение прямых CD и EF на рисунке 221?
317. Угол ABC равен 60°, а угол BCD — 120°. Можно ли утверждать, что прямые AB и CD параллельны?
318. Угол между прямыми a и c равен углу между прямыми b и c . Можно ли утверждать, что прямые a и b параллельны?
319. Четыре угла, образованные при пересечении прямых a и b прямой c , равны по 40°, а любой из остальных четырёх углов — 140°. Можно ли утверждать, что прямые a и b параллельны?
320. Прямая пересекает биссектрису BM треугольника ABC в точке O , являющейся серединой отрезка BM , а сторону BC — в точке K . Докажите, что если OK ⊥ BM , то MK ‖ AB .
321. Отрезки AM и CK — медианы треугольника ABC . На продолжении отрезка AM за точку M отложен отрезок MF , а на продолжении отрезка CK за точку K — отрезок KD так, что MF = AM , KD = CK . Докажите, что точки B , D и F лежат на одной прямой.
Упражнения для повторения
322. Луч OC разбивает угол AOB на два угла так, что ∠ AOC : ∠ BOC = 3 : 5. Найдите угол между лучом OC и биссектрисой угла, смежного с углом AOB , если угол BOC на 42° больше угла AOC .
323. На рисунке 222 AB = BC , ∠ ABK = ∠ CBM . Докажите, что BM = BK .
324. Равнобедренные треугольники ABC и ADC имеют общее основание AC . Прямая BD пересекает отрезок AC в точке E . Докажите, что AE = EC .
Наблюдайте, рисуйте, конструируйте, фантазируйте
325. Приведите пример, когда общей частью (пересечением) треугольника и четырёхугольника является восьмиугольник.
Когда сделаны уроки
Пятый постулат Евклида
В § 6 вы узнали, что в качестве аксиом выбирают очевидные утверждения. Тогда почему бы, например, теоремы 1.1 и 5.1 не включить в список аксиом, ведь они тоже очевидны? Ответ на этот вопрос понятен: если какое-то утверждение можно доказать с помощью аксиом, то это утверждение — теорема, а не аксиома. С этих позиций очень поучительна история, связанная с пятым постулатом Евклида
V постулат. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны от секущей, с которой эта сумма меньше двух прямых углов ( рис. 223 ).
Можно показать, что пятый постулат и сформулированная нами в § 13 аксиома параллельности прямых равносильны, т. е. из постулата следует аксиома и наоборот — из аксиомы следует постулат.
Более двадцати веков многие учёные пытались доказать пятый постулат, т. е. вывести его из других аксиом Евклида. Лишь в начале XIX в. несколько математиков независимо друг от друга пришли к выводу: утверждение, что через данную точку, не лежащую на данной прямой, мож но провести только одну прямую, параллельную данной , является аксиомой.
Вам может показаться, что в этом выводе ничего особенного нет: присоединяем аксиому параллельности к уже существующему списку аксиом-правил, а дальше доказываем теоремы.
Однако если в футболе добавить только одно правило, например разрешить полевым игрокам играть и руками, то мы получим совершенно новую игру.
Если пятый постулат — это правило, которое мы принимаем, а не теорема, то его можно заменить противоположным утверждением.
Так и поступил Н.И. Лобачевский. Он заменил лишь одно правило — аксиому параллельности прямых — следующим: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную. Новая аксиома позволила построить новую геометрию — неевклидову.
Н.И. Лобачевский (1792–1856)
Выдающийся русский математик, про-
фессор Казанского университета.
С подобной идеей несколько позже выступил венгерский математик Янош Бойяи (1802–1860).
🎬 Видео
№204 Концы отрезка АВ лежат на параллельных прямых а и b. Прямая, проходящая через середину ОСкачать

№191. Отрезок ВК — биссектриса треугольника ABC. Через точку К проведена прямая, пересекающаяСкачать
Высота, биссектриса, медиана. 7 класс.Скачать

№193. В треугольнике ABC ∠A=40°, ∠B=70°. Через вершину B проведена прямая BD так, что луч ВССкачать

Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

№93. Прямые а и b параллельны. Через точку М прямой a проведена прямая MN, отличная от прямой а и неСкачать
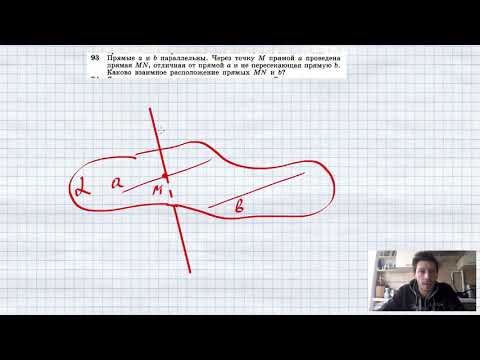
№188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АССкачать
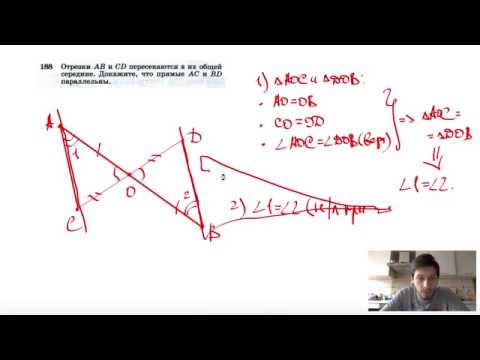
№192. В треугольнике ABC угол А равен 40°, а угол BCE, смежный с углом ACB, равен 80°Скачать

№139. На рисунке 76 АВ = CD, AD = ВС, BE — биссектриса угла ABC, a DF — биссектриса угла ADC.Скачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

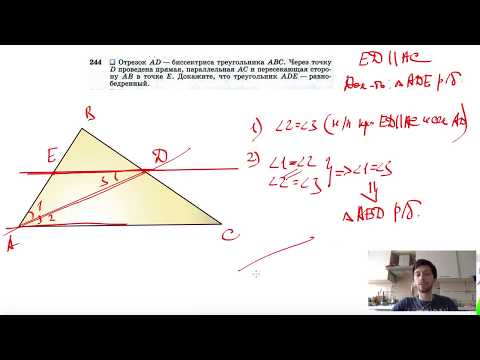
№244. Отрезок AD — биссектриса треугольника ABC. Через точку D проведена прямая, параллельная АССкачать
№198. Прямые а и b перпендикулярны к прямой р, прямая с пересекает прямую а. ПересекаетСкачать

№538. Биссектриса AD треугольника ABC делит сторону ВС на отрезки CD и BD, равные соответственноСкачать

№16. Параллельные прямые a и b лежат в плоскости α. Докажите,Скачать

7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Параллельные прямые (задачи).Скачать

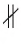
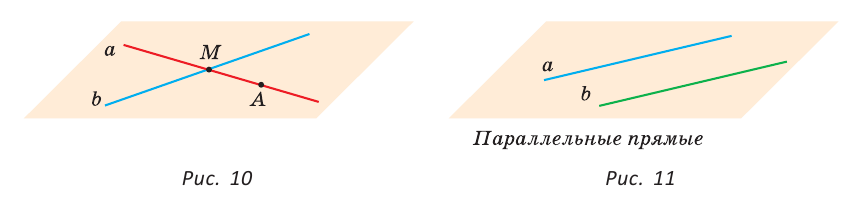
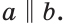
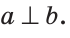
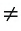 90°, то из середины О отрезка АВ проведем отрезок ОF
90°, то из середины О отрезка АВ проведем отрезок ОF  ОFА =
ОFА = 
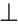
 3 и
3 и 5,
5, 4 и
4 и 6 — внутренние накрест лежащие углы;
6 — внутренние накрест лежащие углы;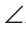 2 и
2 и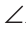 8,
8,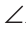 1 и
1 и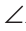 7 — внешние накрест лежащие углы;
7 — внешние накрест лежащие углы; 6,
6, 3 и
3 и 7,
7, 1 и
1 и 5,
5, 4 и
4 и 8 — соответственные углы;
8 — соответственные углы;