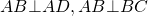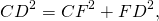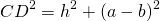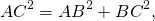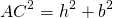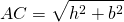В данной статье мы расскажем Вам о свойствах прямоугольной трапеции, как обычной, так и той, в которую вписана окружность.
Для начала напомним некоторые основные определения.
Трапеция – это четырехугольник, имеющий 2 параллельные друг другу стороны, причем 2 другие стороны параллельными не являются.
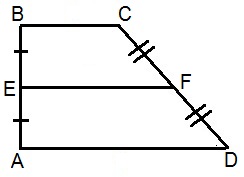
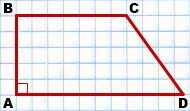
Прямоугольная трапеция — это такая трапеция, одна из боковых сторон которой перпендикулярна ее основаниям (изображена на рис.).
Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон фигуры (на рис. EF).
- Основные свойства прямоугольной трапеции
- Свойства прямоугольной трапеции, в которую вписана окружность
- SABCD = BC * AD
- Свойства трапеции, описанной около окружности: формулы и теоремы
- Элементы, виды и признаки геометрической фигуры трапеция
- Свойства трапеции, описанной около окружности
- Еще немного о свойствах трапеции, заключенной в окружность
- Прямоугольная трапеция
- 🎦 Видео
Видео:Задача про трапецию, описанную около окружностиСкачать

Основные свойства прямоугольной трапеции
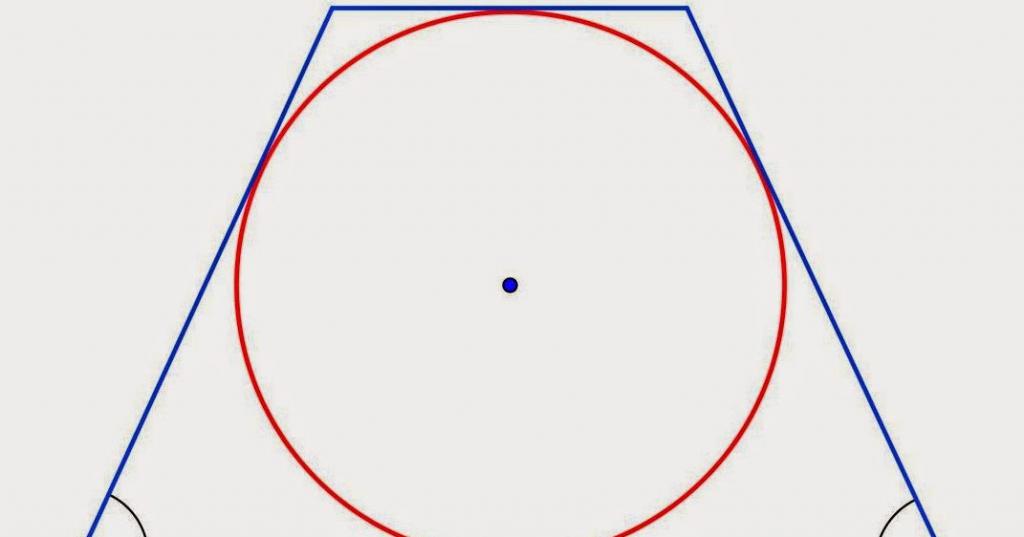
- Средняя линия EF равна половине суммы ее оснований BC и AD.
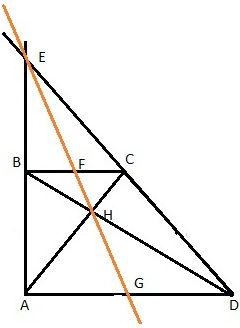
- точка пересечения (H) диагоналей прямоугольной трапеции AC и BD;
- точка пересечения (E) продолжений боковых сторон трапеции AB и CD;
- середины (F и G) оснований трапеции BC и AD.
Данным свойством обладает как прямоугольная, так и равносторонняя трапеция.
Видео:Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать
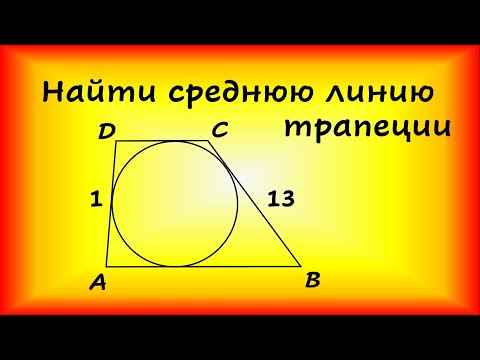
Свойства прямоугольной трапеции, в которую вписана окружность
SABCD = BC * AD
Узнать подробнее о свойствах трапеции с прямым углом, в которую вписана окружность, а также ознакомиться с доказательствами этих свойств, можно на сайте uznateshe.ru.
Понравилась статья, расскажите о ней друзьям:
Видео:2121 периметр прямоугольной трапеции описанной около окружности равен 100Скачать

Свойства трапеции, описанной около окружности: формулы и теоремы
Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».
Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.
Видео:Около трапеции описана окружностьСкачать
Элементы, виды и признаки геометрической фигуры трапеция
Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.
У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:
- Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
- При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
- Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
- При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
- При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
- Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°. Отрезок, соединяющий основания, будет равен 1/2 их разности.
Видео:Периметр прямоуг. трапеции, описанной около окружн., равен 100, ее большая боковая сторона равна 37.Скачать

Свойства трапеции, описанной около окружности
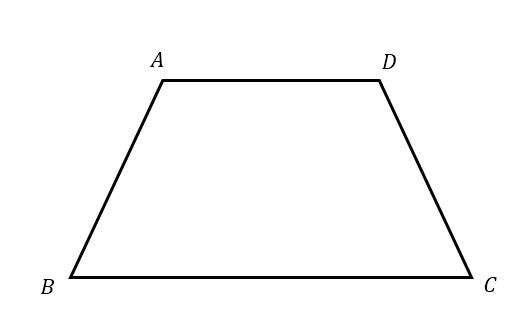
Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.
Итак, подробнее о свойствах трапеции, описанной около окружности:
- Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
- При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
- Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Еще немного о свойствах трапеции, заключенной в окружность
Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.
Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.
На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.
Видео:Радиус описанной окружности трапецииСкачать

Прямоугольная трапеция
Что такое прямоугольная трапеция и какими свойствами она обладает?
Прямоугольная трапеция — это трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Рисунок прямоугольной трапеции
ABCD- прямоугольная трапеция,
AD ∥ BC — основания трапеции,
AB и CD — ее боковые стороны,
Свойства прямоугольной трапеции:
1) Высота прямоугольной трапеции равна ее меньшей боковой стороне.
AB — высота трапеции ABCD.
2) У прямоугольной трапеции два угла — прямые, один — острый и один — тупой.
∠A и ∠B — прямые, ∠D — острый, ∠C — тупой.
3) Высота, проведенная из вершины тупого угла, делит прямоугольную трапецию на прямоугольник и прямоугольный треугольник.
ABCD — прямоугольник (так как у него все углы — прямые). Следовательно, AF=BC, CF=AB.
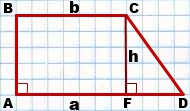
FCD — прямоугольный треугольник. FD=AD-AF,
отсюда FD=AD-BC. Если AD=a, BC=b, CF=AB=h, то
4) Квадрат меньшей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и меньшего основания.

По теореме Пифагора,
5) Квадрат большей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и большего основания.

🎦 Видео
ОГЭ по математике. Задание 15Скачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

✓ Радиус описанной окружности | ЕГЭ. Задание 1. Математика. Профильный уровень | Борис ТрушинСкачать

Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

ЕГЭ. Трапеция, описанная около окружности.Скачать

Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

6 Периметр прямоугольной трапеции, описанной около окружностиСкачать

ЕГЭ математика 2023 Вариант 2 задача 1Скачать
Окружность вписанная в треугольник и описанная около треугольника.Скачать