Прямоугольная диметрия окружности последовательность построения эллипса во фронтальной плоскости (7 видео)

Аксонометрические проекции

Во многих случаях при выполнении технических чертежей оказывается полезным наряду изображением предметов в системе ортогональных проекций иметь более наглядные изображения. Для построения таких изображений применяются проекции, называемые аксонометрическими .

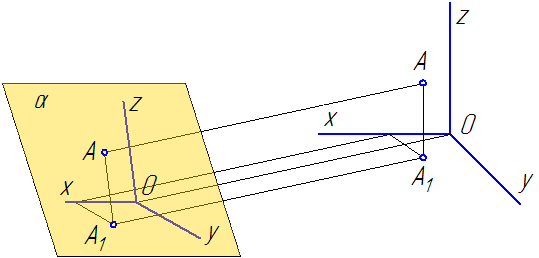
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α (Рисунок 4.1).

Рисунок 4.1p/

Направление проецирования S определяет положение аксонометрических осей на плоскости проекций α, а также коэффициенты искажения по ним. При этом необходимо обеспечить наглядность изображения и возможность производить определения положений и размеров предмета.
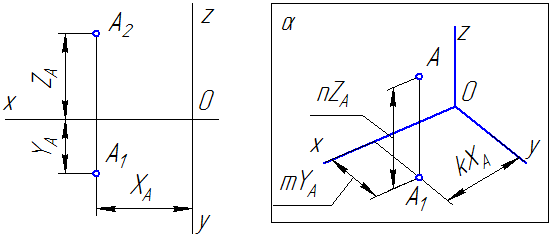
В качестве примера на Рисунке 4.2 показано построение аксонометрической проекции точки А по ее ортогональным проекциям.

Рисунок 4.2

Здесь буквами k, m, n обозначены коэффициенты искажения по осям OX, OY и OZ соответственно. Если все три коэффициента равны между собой, то аксонометрическая проекция называется изометрической, если равны между собой только два коэффициента, то проекция называется диметрической, если же k≠m≠n, то проекция называется триметрической.
Если направление проецирования S перпендикулярно плоскости проекций α, то аксонометрическая проекция носит названия прямоугольной. В противном случае, аксонометрическая проекция называется косоугольной.
ГОСТ 2.317-2011 устанавливает следующие прямоугольные и косоугольные аксонометрические проекции:

прямоугольные изометрические и диметрические;
косоугольные фронтально изометрические, горизонтально изометрические и фронтально диметрические;

Ниже приводятся параметры только трех наиболее часто применяемых на практике аксонометрических проекций.
Каждая такая проекция определяется положением осей, коэффициентами искажения по ним, размерами и направлениями осей эллипсов, расположенных в плоскостях, параллельных координатным плоскостям. Для упрощения геометрических построений коэффициенты искажения по осям, как правило, округляются.

Содержание

4.1. Прямоугольные проекции
4.1.1. Изометрическая проекция
4.1.2. Диметрическая проекция
4.2 Косоугольные проекции
4.2.1 Фронтальная диметрическая проекция
4.3 Построение эллипса
4.3.1 Построения эллипса по двум осям
4.3.2 Построение эллипса по хордам
4.4 Штриховка сечений
Построение окружности в прямоугольной диметрической проекции
Порядок построения фронтальных диметрических проекций
🔍 Видео

Видео:Построение окружности в диметрииСкачать

4.1. Прямоугольные проекции

4.1.1. Изометрическая проекция

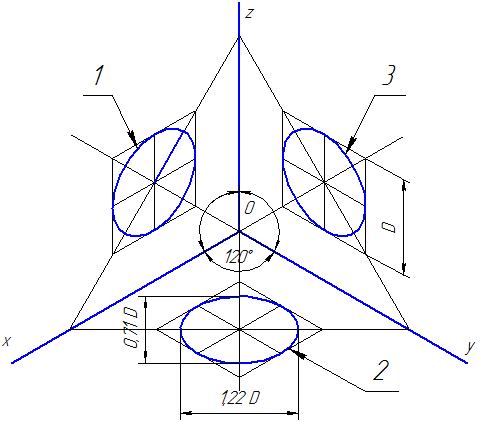
Направление аксонометрических осей приведено на Рисунке 4.3.

Рисунок 4.3 – Аксонометрические оси в прямоугольной изометрической проекции

Действительные коэффициенты искажения по осям OX, OY и OZ равны 0,82. Но с такими значениями коэффициентов искажения работать не удобно, поэтому, на практике, используются приведенные коэффициенты искажений. Эта проекция обычно выполняется без искажения, поэтому, приведенные коэффициенты искажений принимается k = m = n =1. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются в эллипсы, большая ось которых равна 1,22, а малая – 0,71 диаметра образующей окружности D.

Большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

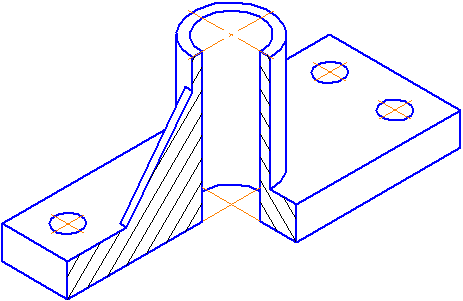
Пример выполнения изометрической проекции условной детали с вырезом приводится на Рисунке 4.4.

Рисунок 4.4 – Изображение детали в прямоугольной изометрической проекции

4.1.2. Диметрическая проекция

Положение аксонометрических осей проводится на Рисунке 4.5.

Для построения угла, приблизительно равного 7º10´, строится прямоугольный треугольник, катеты которого составляют одну и восемь единиц длины; для построения угла, приблизительно равного 41º25´ — катеты треугольника, соответственно, равны семи и восьми единицам длины.

Коэффициенты искажения по осям ОХ и OZ k=n=0,94 а по оси OY – m=0,47. При округлении этих параметров принимается k=n=1 и m=0,5. В этом случае размеры осей эллипсов будут: большая ось эллипса 1 равна 0,95D и эллипсов 2 и 3 – 0,35D (D – диаметр окружности). На Рисунке 4.5 большие оси эллипсов 1, 2 и 3 расположены под углом 90º к осям OY, OZ и OX, соответственно.

Пример прямоугольной диметрической проекции условной детали с вырезом приводится на Рисунке 4.6.

Рисунок 4.5 – Аксонометрические оси в прямоугольной диметрической проекции

Рисунок 4.6 – Изображение детали в прямоугольной диметрической проекции

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

4.2 Косоугольные проекции

4.2.1 Фронтальная диметрическая проекция

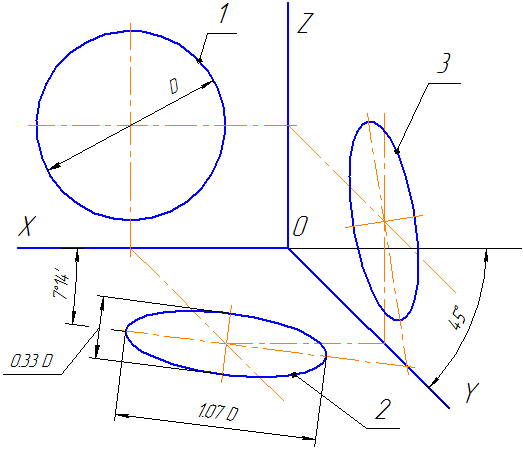
Положение аксонометрических осей приведено на Рисунке 4.7. Допускается применять фронтальные диметрические проекции с углом наклона к оси OY, равным 30 0 и 60 0 .

Коэффициент искажения по оси OY равен m=0,5 а по осям OX и OZ — k=n=1.

Рисунок 4.7 – Аксонометрические оси в косоугольной фронтальной диметрической проекции

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на плоскость XOZ без искажения. Большие оси эллипсов 2 и 3 равны 1,07D, а малая ось – 0,33D (D — диаметр окружности). Большая ось эллипса 2 составляет с осью ОХ угол 7º 14´, а большая ось эллипса 3 составляет такой же угол с осью OZ.

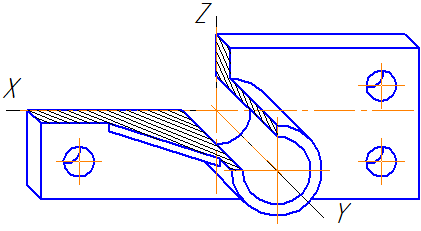
Пример аксонометрической проекции условной детали с вырезом приводится на Рисунке 4.8.

Как видно из рисунка, данная деталь располагается таким образом, чтобы её окружности проецировались на плоскость XОZ без искажения.

Рисунок 4.8 – Изображение детали в косоугольной фронтальной диметрической проекции

Видео:Прямоугольные диметрические проекцииСкачать

4.3 Построение эллипса

4.3.1 Построения эллипса по двум осям

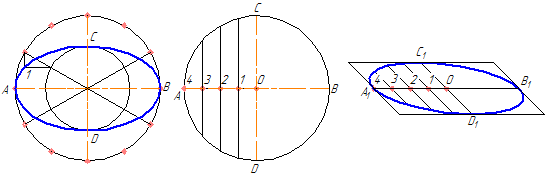
На данных осях эллипса АВ и СD строятся как на диаметрах две концентрические окружности (Рисунок 4.9, а).

Одна из этих окружностей делится на несколько равных (или неравных) частей.

Через точки деления и центр эллипса проводятся радиусы, которые делят также вторую окружность. Затем через точки деления большой окружности проводятся прямые, параллельные линии АВ.

Точки пересечения соответствующих прямых и будут точками, принадлежащими эллипсу. На Рисунке 4.9, а показана лишь одна искомая точка 1.

а б в
Рисунок 4.9 – Построение эллипса по двум осям (а), по хордам (б)

4.3.2 Построение эллипса по хордам

Диаметр окружности АВ делится на несколько равных частей, на рисунке 4.9,б их 4. Через точки 1-3 проводятся хорды параллельно диаметру CD. В любой аксонометрической проекции (например, в косоугольной диметрической) изображаются эти же диаметры с учетом коэффициента искажения. Так на Рисунке 4.9,б А₁В₁=АВ и С₁ D₁ = 0,5CD. Диаметр А ₁В₁ делится на то же число равных частей, что и диаметр АВ, через полученные точки 1-3 проводятся отрезки, равные соответственным хордам, умноженным на коэффициент искажение (в нашем случае – 0,5).

4.4 Штриховка сечений

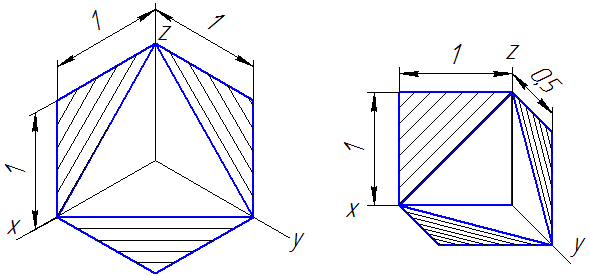
Линии штриховки сечений (разрезов) в аксонометрических проекциях наносятся параллельно одной из диагоналей квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (Рисунок 4.10: а – штриховка в прямоугольной изометрии; б – штриховка в косоугольной фронтальной диметрии).

а б
Рисунок 4.10 – Примеры штриховки в аксонометрических проекциях

Видео:Построение прямоугольной изометрии окружностиСкачать

Построение окружности в прямоугольной диметрической проекции

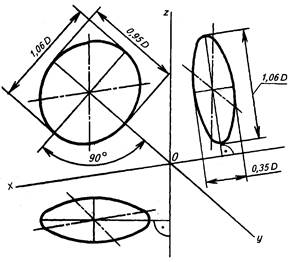
В прямоугольной диметрии окружности проецируются в виде эллипсов, малые оси которых, как и в изометрии, параллельны осям, отсутствующим в плоскостях данных окружностей. Например, для эллипса, лежащего в горизонтальной плоскости, малая ось идет по направлению оси z’, а большая — перпендикулярна к ней (рис. 3.55).

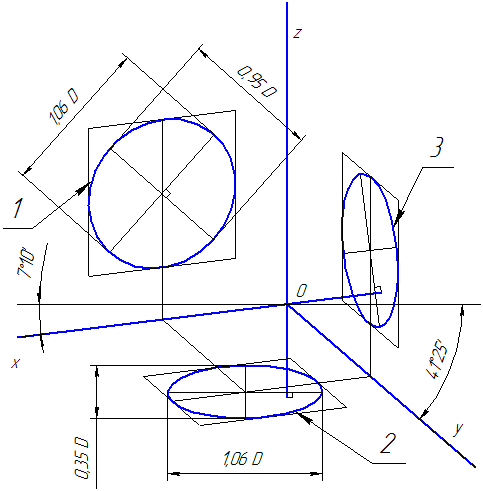
Изображение окружностей в прямоугольной диметрии

Длина большой оси для всех эллипсов одинакова и равна 1,06D диаметра изображаемой окружности. Величина малой оси различна: для фронтальной плоскости проекций величина малой оси равна 0,95-0,95D длины большой оси, или 0,95 диаметра окружности (0,95D); для горизонтальной и профильной плоскостей и для плоскостей, параллельных им, величина малой оси равна 1/3 большой оси, то есть 0,35 диаметра окружности (0,35D).

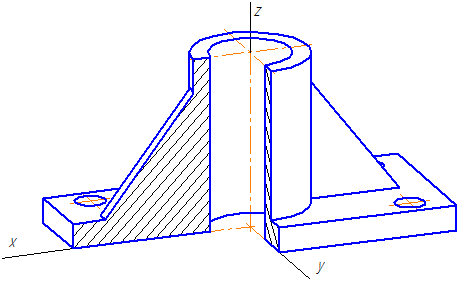
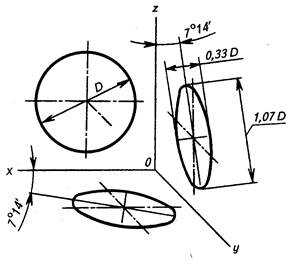
Во фронтальной диметрической проекции окружность, лежащая в плоскости П„изображается без искажения. Это обстоятельство представляет существенное преимущество при вычерчивании фронтальной диметрии деталей цилиндрической формы или с большим числом цилиндрических отверстий (рис. 3.57).

Окружности, спроецированные на плоскости П₁ и П₂, изображаются эллипсами, у которых большая ось этих эллипсов равна 1,07D, а малая — 0,33D. В отличие от прямоугольной диметрии, большая ось эллипса в плоскости П₁ наклонена к горизонтальному направлению под углом 7 о 14′, а в профильной плоскости — под тем же углом к вертикальному направлению. Упрощенное построение эллипсов в виде овалов выполняют по тем же правилам, что и в прямоугольной диметрии.

Изображение окружностей во фронтальной диметрии

Видео:Построение эллипса по восьми точкам в прямоугольной диметрииСкачать

Порядок построения фронтальных диметрических проекций

Рассмотрим порядок построения фронтальной диметрической проекции предмета, три вида которого приведены на рис. 3.5, а.

Вначале проводят оси (рис. 3.5, б). Затем в плоскости xOz строят изображение передней грани (рис. 3.5, в). При этом все отрезки вертикальных прямых линий проводят параллельно оси 2, а отрезки горизонтальных прямых – параллельно оси х. Чтобы выполнить построение, от точки О по оси х откладывают ширину предмета – размер 50 мм. Затем из конца отложенного отрезка восставляют перпендикуляр и откладывают на нем размер высоты (90 мм), так как высота параллельна оси z. Верхняя сторона фигуры параллельна нижней, поэтому из конца полученного отрезка проводят прямую, параллельную оси х, и откладывают на ней соответствующий размер (20 мм). Из полученной точки проводят линию, параллельную оси z. От точки О по оси z откладывают высоту, равную 40 мм, и из полученной точки проводят линию, параллельную оси х. Таким образом, передняя грань предмета изображена.

Рис. 3.5. Порядок построения фронтальной диметрической проекции предмета

Затем проводят линии, соответствующие ребрам, перпендикулярным передней грани призмы. Их вычерчивают параллельными оси у.

Ось у показывает на чертеже направление, перпендикулярное плоскости xOz. Поэтому толщину предмета откладывают параллельно оси у, т.е. под углом 45°. Длина всех ребер одинакова, так как передняя грань параллельна задней. На всех прямых, расположенных под углом 45°, нужно было бы отложить одинаковые отрезки длиной по 60 мм. Но так как по оси у все размеры сокращают наполовину, то откладывают по 30 мм (рис. 3.5, д). Полученные точки последовательно соединяют прямыми (рис. 3.5, е).

Построение легко проверить. Ребра, ограничивающие заднюю грань, параллельны соответствующим ребрам передней грани. Следовательно, и на чертеже они должны быть взаимно параллельны. Если это не получилось, проекция построена неверно.

Затем обводят видимый контур и наносят размеры (рис. 3.5, ж). Размерные и выносные линии в наглядных изображениях располагают параллельно аксонометрическим осям.

Рассмотрим построение фронтальной диметрической проекции правильной треугольной призмы, два вида которой даны на рис. 3.6, а. Построение проведено следующим образом. Вычерчены оси (рис. 3.6, б). Затем построена фигура основания призмы – равносторонний треугольник (рис. 3.6, в). Для этого по оси х в обе стороны от точки О отложено по половине длины стороны основания: отрезки прямых по 40 мм. От точки О по оси у отложен отрезок, равный половине высоты треугольника. Три полученные точки соединены прямыми, которые образовали аксонометрическое изображение равностороннего треугольника. Затем из вершин полученного треугольника проведены линии, изображающие вертикальные ребра призмы (рис. 3.6, г). На одном из них отложена высота вычерчиваемого тела, равная 100 мм. Ребра верхнего основания проведены параллельно соответствующим ребрам нижнего основания, как это имеет место в действительности. Невидимое ребро проведено штриховой линией, обведен видимый контур и проставлены размеры (рис. 3.6, д).

Рис. 3.6. Последовательность построения фронтальной диметрической проекции треугольной призмы

Построение фронтальной диметрической проекции правильной шестиугольной призмы выполнено так (рис. 3.7, а). В окружность с центром в точке О пересечения осей вписан шестиугольник (рис. 3.7, б) со стороной, равной 40 мм. Ребра проведены под углом 45°, т. е. параллельно оси у (рис. 3.7, в). На одном из ребер отложен сокращенный вдвое размер высоты – 50 мм, и на этом расстоянии проведены параллельные сторонам шестиугольника прямые, изображающие видимые ребра основания призмы (рис. 3.7, г), затем обведен видимый контур и поставлены размеры (рис. 3.7, д).

Рис. 3.7. Последовательность построения фронтальной диметрической проекции шестиугольной призмы

Правильную четырехугольную пирамиду во фронтальной диметрической проекции, два вида которой представлены на рис. 3.8, а, легко изобразить, начиная с фигуры основания. Для этого откладывают по оси х полный размер стороны основания пирамиды, а по оси у – размер, сокращенный вдвое (рис. 3.8, б). Через полученные точки проводят отрезки прямых, параллельные осям х и у, получая фронтальную диметрическую проекцию квадрата, являющегося основанием пирамиды.

По оси z от точки О откладывают высоту пирамиды и полученную точку соединяют с вершинами основания (рис. 3.8, в). Затем обводят видимый и невидимый контуры, наносят размеры (рис. 3.8, г).

Рис. 3.8. Последовательность построения фронтальной диметрической проекции четырехугольной пирамиды

Как видно из построения, высота пирамиды совпадает с осью z. Такое положение изображаемого объекта, когда его высота, сторона основания, боковые ребра и другие элементы параллельны осям х, у, z, соответственно является предпочтительным, так как это облегчает построение аксонометрических проекций.

Рассмотрим вычерчивание наглядного изображения детали, имеющей выступ (рис. 3.9, а). В этом случае важно выбрать правильный порядок выполнения чертежа. Построение не следует начинать с выступа, лучше сначала вычертить тело детали, а затем пристроить выступ, как это сделано на рис. 3.9, б – д.

Рис. 3.9. Последовательность построения фронтальной диметрической проекции детали, имеющей выступ

Рассмотрев несколько случаев построения фронтальных диметрических проекций разных деталей, можно сделать вывод, что выбор последовательности построения наглядного изображения зависит от формы детали. В одних случаях целесообразно начинать чертить с изображения передней грани, в других – с основания предмета, иногда – с задней грани. Но во всех случаях необходимо придерживаться следующих правил:

• ребра, перпендикулярные плоскости хОу, проводить параллельно оси у,
• параллельные элементы предметов сохранять параллельными и в аксонометрической проекции;
• все отрезки прямых линий, которые в натуре имели направление, параллельное осям х, у или z, оставлять параллельными тем же осям и в наглядном изображении;
• располагать изображаемый объект целесообразно так, чтобы основные его элементы совпадали с осями проекций.