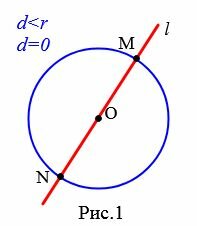
Прямая и окружность имеют две точки если (3 видео)

Взаимное расположение прямой и окружности

Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.

Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.

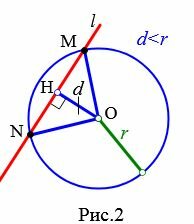Прямая и окружность имеют две точки если

Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.

В этом случае прямая называется секущей по отношению к окружности.

Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.

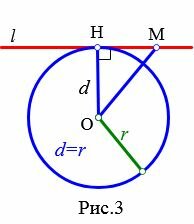Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.

Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

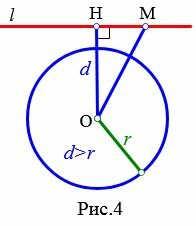Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

Содержание

Please wait.
We are checking your browser. megamozg.com
Why do I have to complete a CAPTCHA?
What can I do to prevent this in the future?
Геометрия. 8 класс
🎦 Видео

Видео:№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Please wait.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

We are checking your browser. megamozg.com

Видео:Прямая и окружность. Математика. 6 класс.Скачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d3362e66ee77a43 • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Видео:Окружность и круг, 6 классСкачать

Геометрия. 8 класс

Конспект
Рассмотрим окружность с центром в точке О и прямую a, её не пересекающую.
Расстояние от центра окружности до прямой равно длине перпендикуляра ОВ.

Это расстояние больше радиуса окружности.
Будем перемещать прямую, параллельно самой себе в сторону центра окружности. В определённый момент, прямая коснется окружности.

Расстояние от центра окружности до прямой равно радиусу окружности.
Прямая, имеющая с окружностью только одну общую точку называется касательной к окружности.
Общая точка прямой и окружности называется точкой касания.
Будем передвигать прямую далее к центру. Прямая пересечет окружность в двух точках.
Расстояние от центра окружности до прямой меньше радиуса.

Продолжая движение дальше, мы получим еще одну касательную к окружности.

Продолжим движение прямой дальше, она опять не будет иметь с окружностью общих точек.
Расстояние от центра окружности опять больше её радиуса.

Рассмотрим случай, когда прямая имеет с окружностью одну общую точку.

Сформулируем свойство касательной.
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Дано: Окружность с центром О, a – касательная, B – точка касания.
Доказать: a ⊥ OB
Доказательство:
Пусть утверждение неверно, т.е. прямая a не перпендикулярна радиусу OB. Тогда OB – наклонная к прямой a. Перпендикуляр меньше наклонной, тогда расстояние от центра O до прямой a меньше радиуса. Следовательно, прямая a и окружность имеют 2 общие точки. Но это противоречит условию, т.к. прямая a – касательная. Значит наше предположение неверно и a ⊥ OB.
Верно и обратное утверждение:
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Проведем к окружности две касательные из одной точки, не принадлежащей окружности.

Выполняется утверждение:
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Докажите его самостоятельно, используя равенство треугольников AOВ и AOС.
Дано: окружность с центром O, касательные AB и AC
Доказать: AB = AC, ∠OAB = ∠OAC
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.