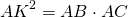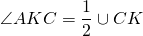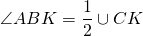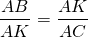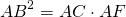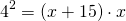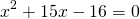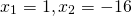Пропорциональность отрезков в окружности

Теорема 111. 1) Перпендикуляр, опущенный из какой-нибудь точки окружности на диаметр, среднепропорционален между частями диаметра. Этот перпендикуляр называется иногда ординатой.

2) Хорда, соединяющая конец диаметра с точкой окружности, среднепропорциональна между диаметром и отрезком, прилежащем хорде.

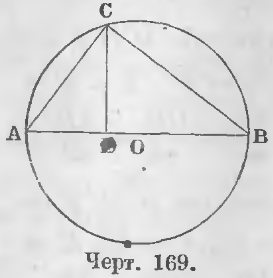
Дано. Опустим из какой-нибудь точки C окружности перпендикуляр CD на диаметр AB (черт. 169).

Требуется доказать, что 1) AD/CD = CD/DB, а также 2) AD/AC = AC/AB.

Доказательство. Соединим точку C с концами диаметра AB, тогда при точке C образуется прямой угол ACB, в котором отрезок CD есть перпендикуляр, опущенный из вершины прямого угла на гипотенузу.

На основании теоремы 100 имеет место пропорция:

на основании теоремы 101 пропорция:

AD/AC = AC/AB, DB/CB = CB/AB (1)

Следствие. Квадраты хорд относятся как соответствующие отрезки диаметра.

Доказательство. Из пропорции (1) следуют равенства:

AC 2 = AB · AD, CB 2 = AB · BD

откуда по разделении находим:

AC 2 /CB 2 = AD/DB.

Теорема 112. Части пересекающихся хорд обратно пропорциональны между собой.

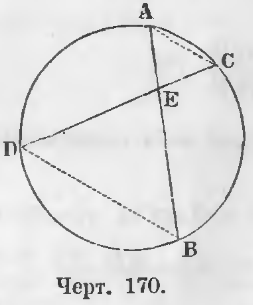
Даны две пересекающиеся хорды AB и CD (черт. 170).

Требуется доказать, что

т. е. большая часть первой хорды относится к большей части второй как меньшая часть второй хорды к меньшей части первой.

Доказательство. Соединим точку A с C и B с D, тогда образуются два подобных треугольника ACE и DBE, ибо углы при точке E равны как вертикальные, ∠CAB = ∠CDB как опирающиеся на концы дуги CB, ∠ACD = ∠ABD как опирающиеся на концы дуги AD.

Из подобия треугольников ACE и DBE вытекает пропорция:

Из пропорции (a) вытекает равенство:

показывающее, что произведение отрезков одной равно произведению отрезков другой хорды.

Теорема 113. Две секущие, проведенные из одной и той же точки вне окружности, обратно пропорциональны внешним своим частям.

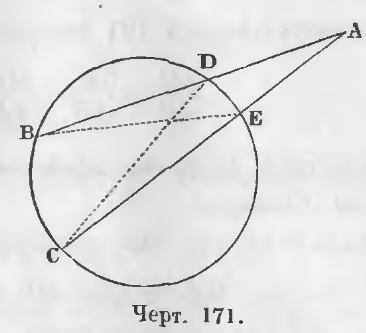
Даны две секущие AB и AC, проведенные из точки A (черт 171).

Требуется доказать, что

т. е. первая секущая относится ко второй, как внешняя часть второй относится к внешней части первой секущей.

Доказательство. Соединим точки D с C, а B с E.

Два треугольника ∠ABE и ∠ADC подобны, ибо угол A общий, B = C как опирающиеся на концы одной и той же дуги DE, следовательно и ∠ADC = ∠AEB.

Из подобия треугольников ADC и ABE вытекает пропорция:

Из этой же пропорции вытекает равенство

показывающее, что произведение секущей на ее внешний отрезок равно произведению другой секущей на ее отрезок (если секущие выходят из одной точки).

Теорема 114. Касательная среднепропорциональна между целой секущей и внешней ее частью.

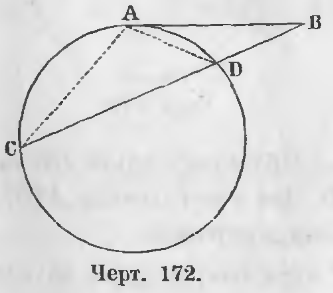
Дана касательная AB и секущая BC (черт. 172).

Требуется доказать, что

Доказательство. Соединим точку A с точками C и D.

Треугольники ABC и ABD подобны, ибо угол B общий, ∠BAD = ∠ACD, следовательно, ∠CAB = ∠ADB.

Из подобия этих треугольников вытекает пропорция:

Из этой пропорции вытекает равенство:

показывающее, что квадрат касательной равен произведению секущей на внешнюю ее часть.

Свойство сторон вписанного четырехугольника

Теорема 115. Во всяком четырехугольнике, вписанном в круг, произведение диагоналей равно сумме произведений противоположных сторон.

Это предположение, известное под именем теоремы Птоломея, встречается в первый раз в сочинении Птоломея «Альагест» во II веке по Р. Х.

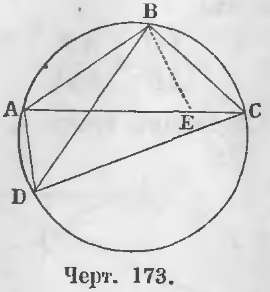
Дан вписанный четырехугольник ABCD (черт. 173) и проведены диагонали AC и BD.

Требуется доказать, что AC · BD = AB · CD + BC · AD.

Доказательство. Проведем прямую BE так, чтобы угол EBC равнялся углу ABD. Два треугольника ABD и BEC подобны, ибо ∠ABD = ∠CBE по построению, ∠ADB = ∠BCE как опирающиеся на одну и ту же дугу AB, следовательно,

Из подобия этих треугольников вытекает пропорция:

Треугольники ABE и BCD подобны, ибо ∠ABE = ∠DBC по построению, ∠BAE = ∠BDC как опирающиеся на дугу BC, следовательно,

Из подобия этих треугольников вытекает пропорция:

Из пропорций (a) и (b) вытекают равенства:

BC · AD = BD · EC
AB · CD = BD · AE

Сложив эти равенства, имеем:

BC · AD + AB · CD = BD · EC + BD · AE = BD (EC + AE)

Так как EC + AE = AC, то

BD · AC = BC · AD + AB · CD (ЧТД).

Теорема 116. Во всяком вписанном четырехугольнике диагонали относятся как суммы произведений сторон, опирающихся на концы диагоналей.

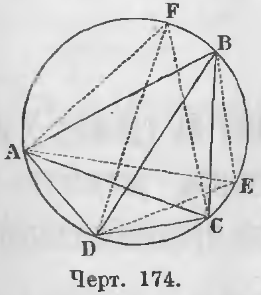
Дан вписанный четырехугольник ABCD (черт. 174) и проведены диагонали AC и BD.

Требуется доказать, что

BD/AC = (AD · DC + AB · BC) / (BC · CD + AD · AB)

Доказательство. а) От точки B отложим дугу BE равную DC и соединим точку E с точками A, B, D.

Для вписанного четырехугольника ABED имеет место равенство:

AE · BD = AD · BE + AB · DE.

Так как BE = CD по построению, DE = BC, ибо ◡DE = ◡DC + ◡CE и ◡BC = ◡BE + ◡CE.

Заменив BE и DE их величинами, имеем равенство:

AE · BD = AD · CD + AB · BC (a)

b) Отложив от точки A дугу AF равную дуге BC и соединив точку F с точками A, D, C, имеем для четырехугольника AFCD равенство:

AC · DF = AF · CD + AD · CF

В этом равенстве AF = BC по построению, CF = AB (ибо ◡CF = ◡BC + ◡BF и ◡AB = ◡AF + ◡BF = ◡BC + ◡BF)

Заменяя величины AF и CF их величинами, найдем равенство:

AC · DF = BC · CD + AD · AB (b)

В равенствах (a) и (b) отрезки AE и DF равны, ибо

◡ADE = AD + DE = ◡AD + ◡BC = ◡AD + ◡AF = ◡DAF

Разделяя равенства (a) и (b), находим:

BC/AD = (AD · C D + AB · BC) / (BC · CD + AD · AB) (ЧТД).

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Свойство касательной и секущей

Теорема о пропорциональности отрезков секущей и касательной

(Свойство касательной и секущей, проведённых из одной точки)

Для касательной и секущей к окружности, проведённых из одной точки, квадрат расстояния от этой точки до точки касания равен произведению длины секущей на длину её внешней части.

Другими словами, квадрат расстояния от данной точки до точки касания равен произведению расстояний от этой точки до точек пересечения секущей с окружностью.

Дано : окр. (O;R), AK — касательная, AB — секущая,

окр. (O;R)∩AK=K, (O;R)∩AB=B, C

Проведём хорды BK и CK.

Рассмотрим треугольники ABK и AKC.

(как вписанный угол, опирающийся на дугу CK).

Значит, треугольники ABK и AKC подобны (по двум углам).

Из подобия треугольников следует пропорциональность их соответствующих сторон:

По основному свойству пропорции

Что и требовалось доказать .

Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найти AC, если диаметр окружности равен 15, а AB=4.

Дано :

∆ABC, B, C ∈ окр.(O;R) O∈AC, AB — касательная, AB=4, FC — диаметр, FС=15

По свойству касательной и секущей, проведённых из одной точки,

Пусть AF=x, тогда AC=x+15. Составим и решим уравнение:

Второй корень не подходит по смыслу задачи. Следовательно, AC=1+15=16.

📹 Видео