При изображении окружности в стандартной изометрии большие оси получающихся

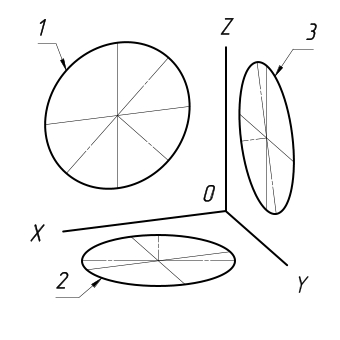
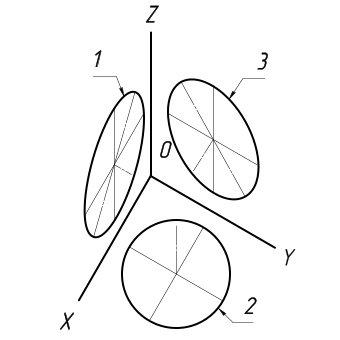
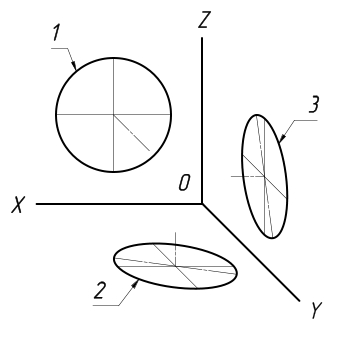
В общем случае окружность проецируется в эллипс, если плоскость окружности расположена под углом к плоскости проекции. Следовательно, аксонометрией окружности будет эллипс. Для построения прямоугольной аксонометрии окружностей, лежащих в координатных или им параллельных плоскостях, руководствуются правилом: большая ось эллипса перпендикулярна аксонометрии той координатной оси, которая отсутствует в плоскости окружности.

В прямоугольной изометрии равные окружности, расположенные в координатных плоскостях, проецируются в равные эллипсы (рис. 2).

Просмотр содержимого документа
«ОКРУЖНОСТЬ В ИЗОМЕТРИИ»

АКСОНОМЕТРИЯ ОБЪЕМНЫХ ТЕЛ.

ОКРУЖНОСТЬ В ИЗОМЕТРИИ.

Научить строить оси аксонометрических проекций. Строить аксонометрические проекции плоских фигур.

Развитие пространственного мышления.

Содействовать в развитии умений использования чертёжных инструментов при графических построениях, в развитии умений выполнять нанесения размеров на чертежах.

Содействовать в воспитании у уч-ся аккуратности, усидчивости в работе.

Методы: Рассказ, объяснение, демонстрация.

Оборудование: Учебник, чертёжные инструменты, учебная презентация.

Тип урока: Получение новых знаний.

Орг. момент – 1-2 мин.

Новый материал – 20мин.

Закрепление – 15 мин.

Заключительная часть урока – 2-3 мин.

Прямоугольная изометрия характеризуется тем, что коэффициенты искажения составляют 0,82. Их получают из соотношения (1).

Для прямоугольной изометрии из соотношения (1) получаем:

Зu2 = 2, или и = v — w = (2/3)1/2 = 0,82, (1)

т. е. отрезок координатной оси длиной 100 мм в прямоугольной изометрии изобразится отрезком аксонометрической оси длиной 82 мм. При практических построениях пользоваться такими коэффициентами искажения не совсем удобно, поэтому ГОСТ 2.317—69 рекомендует пользоваться приведенными коэффициентами искажения:

Построенное таким образом изображение будет больше самого предмета в 1,22 раза, т. е. масштаб изображения в прямоугольной изометрии будет МА 1,22: 1.

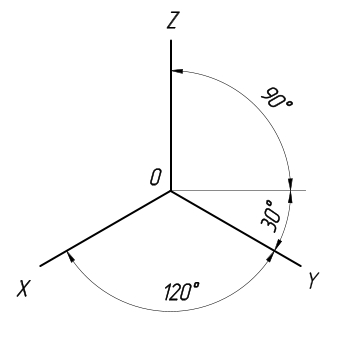
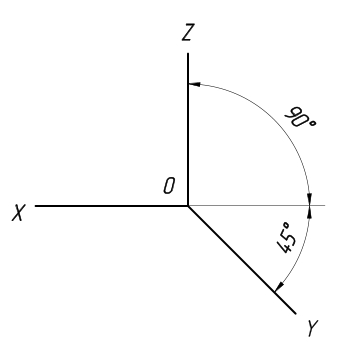
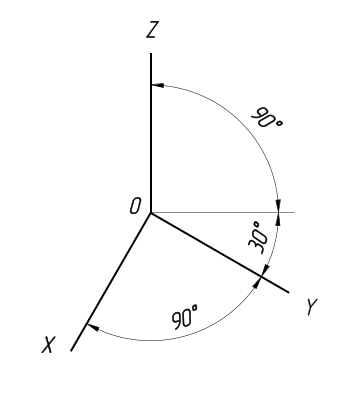
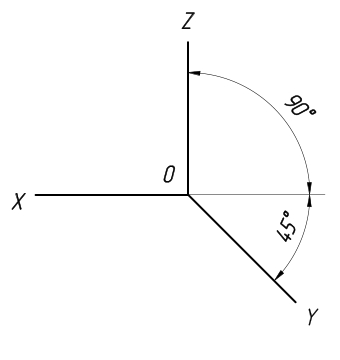
Аксонометрические оси в прямоугольной изометрии располагаются под углом 120° друг к другу (рис. 1). Изображение окружности в аксонометрии представляет интерес, особенно окружностей, принадлежащих координатным или им параллельным плоскостям.

Рис. 1 Аксонометрические оси в прямоугольной изометрии

В общем случае окружность проецируется в эллипс, если плоскость окружности расположена под углом к плоскости проекции. Следовательно, аксонометрией окружности будет эллипс. Для построения прямоугольной аксонометрии окружностей, лежащих в координатных или им параллельных плоскостях, руководствуются правилом: большая ось эллипса перпендикулярна аксонометрии той координатной оси, которая отсутствует в плоскости окружности.

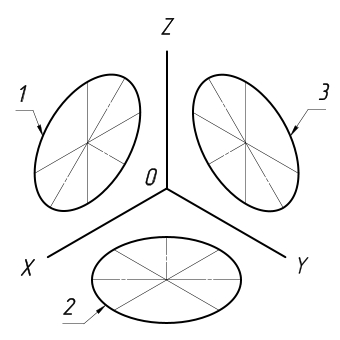
В прямоугольной изометрии равные окружности, расположенные в координатных плоскостях, проецируются в равные эллипсы (рис. 2).

Рис. 2 Равные окружности, расположенные в координатных плоскостях, проецируются в равные эллипсы

Размеры осей эллипсов при использовании приведенных коэффициентов искажения равны:

большая ось 2а= 1,22d,

малая ось 2b = 0,71d,

где d — диаметр изображаемой окружности.

Эллипс, как изометрию окружности, можно построить по восьми точкам, ограничивающим его большую и малую оси и проекции диаметров, параллельных координатным осям.

В практике инженерной графики эллипс, являющийся изометрией окружности, лежащей в координатной или ей параллельной плоскости, можно заменить четырехцентровым овалом, имеющим такие же оси:

2a = 1,22d и 2b = 0,71 d.

На рис. 3 показано построение осей такого овала для изометрии окружности диаметра d.

Рис. 3 Построение осей овала для изометрии окружности

Для построения аксонометрии окружности, расположенной в проецирующей плоскости или плоскости общего положения, нужно выделить на окружности некоторое число точек, построить аксонометрию этих точек и соединить их плавной кривой; получим искомый эллипс — аксонометрию окружности (рис. 4).

Рис. 4 Построение аксонометрии окружности

На окружности, расположенной в горизонтально проецирующей плоскости, взято 8 точек (1,2. 8). Сама окружность отнесена к натуральной системе координат (рис. 4, а).Проводим оси эллипса прямоугольной изометрии и, используя приведенные коэффициенты искажения, строим вторичную проекцию окружности 11 1. 511 по координатам х и у (рис. 4, б). Достраивая аксонометрические координатные ломаные для каждой из восьми точек, получаем их изометрию (11, 21, . 81). Соединяем плавной кривой изометрические проекции всех точек и получаем изометрию заданной окружности.

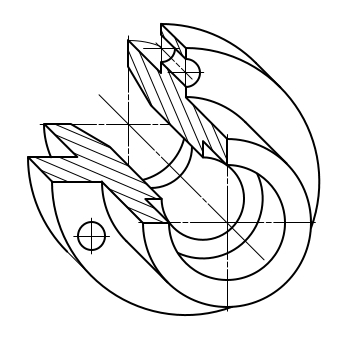
Изображение геометрических поверхностей в прямоугольной изометрии рассмотрим на примере построения стандартной прямоугольной изометрии усеченного прямого кругового конуса (рис. 5).

Рис. 5 Прямоуголая изометрия усеченного прямого кругового конуса

На комплексном чертеже изображен конус вращения, усеченный горизонтальной плоскостью уровня, расположенной на высоте z от нижнего основания, и профильной плоскостью уровня, дающей в сечении на поверхности конуса гиперболу с вершиной в точке А. Проекции гиперболы построены по отдельным ее точкам.

Отнесем конус к натуральной системе координат Oxyz. Построим проекции натуральных осей на комплексном чертеже и отдельно их изометрическую проекцию. Построение изометрии начинаем с построения эллипсов верхнего и нижнего оснований, которые являются изометрическими проекциями окружностей оснований. Малые оси эллипсов совпадают с направлением изометрической оси ОZ (см. рис. 2). Большие оси эллипсов перпендикулярны малым. Величины эллипсов осей определяются в зависимости от величины диаметра окружности (d — нижнего основания и d1 — верхнего основания). Затем строят изометрию сечения конической поверхности профильной плоскости уровня, которая пересекает основание по прямой, отстоящей от начала координат на величинуXA и параллельной оси Оу.

Изометрия точек гиперболы строится по координатам, замеряемым на комплексном чертеже, и откладываем без изменения вдоль соответствующих изометрических осей, так как приведенные коэффициенты искажения и = v = w = 1. Изометрические проекции точек гиперболы соединяем плавной кривой. Построение изображения конуса заканчивается проведением очерковых образующих касательной к эллипсам оснований. Невидимая часть эллипса нижнего основания проводится штриховой линией.

Подведение итога. Какие размеры откладывают при выполнении чертежа вдоль аксонометрических осей в изометрической и фронтальной диметрической проекциях?

ДОМАШНЕЕ ЗАДАНИЕ: выполнить чертех эллипса:

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Изображение окружностей на аксонометрических плоскостях

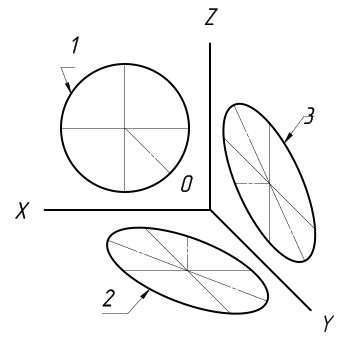
В прямоугольной изометрической проекции окружности, расположенные в плоскостях, параллельных плоскостям П₁, П₂, П₃, изображаются эллипсами. Они строятся по большой и малой осям, которые равны 1,22d и 0,77d или заменяются овалами. Построение эллипсов представлено на рис. 5.3. В прямоугольной диметрической проекции окружность, расположенная во фронтальной плоскости , проецируется в эллипс с осями, равными 1,06d и 0,94d. Окружности, расположенные в горизонтальной и профильной плоскостях, проецируются в одинаковые эллипсы с осями, равными 1,06d и 0,35d. Построение эллипсов в диметрии представлено на рис. 5.3. Построение эллипсов в аксонометрии часто заменяется построением четырехцентровых овалов, представленные на рис. 5.4.

Построение эллипса по восьми точкам.Построение эллипса по восьми точкам начинаем с построение большой оси, всегда расположенной перпендикулярно отсутствующей в плоскости оси( отрезок 1-2). Малая соь эллипса располагается перпендикулярно большой оси эллипса и, следовательно, совпадает с отсутствующей в плоскости осью ( отрезок 3-4-).

Церез центр эллипса проводятся аксонометрические оси, находящиеся в данной плоскости и на них откладываются отрезки равные диаметру окружности отрезки, которую строят в изометрии ( отрезок 7 – 8)и во фронтальной плоскости для диметрии ( отрезки 5 – 6). В горизонтальной и профильной плоскости для диметрии вдоль оси Y откладывается отрезок равный 0,5d ( отрезок 7 – 8)

При построении наглядных изображений на практике используют чаще всего аксонометрические проекции, приведенные в ГОСТе 2.317-69*.

При выборе вида аксонометрических изображений следует руководствоваться такими рекомендациями:

1. Изометрическую проекцию следует применять тогда, когда все три стороны объекта имеют приблизительно одинаковое количество особенностей;

2. Прямоугольную диметрическую проекцию применяют в случаях, когда только одна сторона объекта содержит наибольшее количество особенностей;

3. Косоугольную диметрическую проекцию применяют тогда, когда объект имеет ряд окружностей, расположенных в плоскостях параллельных П₂.

Из прямоугольных аксонометрических проекций лучше выбирать диметрическую проекцию или прямоугольную изометрию. Прямоугольная изометрическая проекция проще в построении, так как при этом коэффициенты искажения по всем осям равны между собой и равны:

Для упрощения построения объектов в изометрии коэффициенты искажения округляются до 1 , но изображение при этом получается увеличенным. Для прямоугольной диметрии выбираются коэффициенты искажения равными:

Для упрощения вычисления размеров при построении диметрической проекции объекта коэффициенты искажения округляются и принимаются равными:

Для построения объекта в аксонометрии необходимо сначала построить его проекционный чертеж, а затем используется способ координат. В этом случае аксонометрические проекции объекта строятся по координатам отдельных точек, взятым с ортогонального чертежа. Построение , как правило , начинается с построения вторичной проекций точек. В качестве вторичной проекции чаще всего используем горизонтальную проекцию точки. Затем из горизонтальной вторичной проекции проводим прямую, параллельную оси Z ( строго вертикальную прямую). На ней откладываем координату Z точки и получаем первичную проекцию, т.е.ее аксонометрическую изображение( рис. 5.5).

При построении прямоугольной изометрической проекции шестигранной призмы используем ортогональный чертеж призмы шестиугольника ( рис. 5.6). За оси координат принимаем оси симметрии. Затем проводим аксонометрические оси. Далее от начала координат откладываем вершины шестиугольника вдоль оси Х , находим остальные вершины на отрезках параллельных оси Y. Построив нижнее основание призмы откладываем высоту призмы и строим параллельное верхнее основание.

Используя ортогональный чертеж пирамиды и задавшись видом аксонометрии, строим ее аксонометрическое изображение( рис. 5.6).

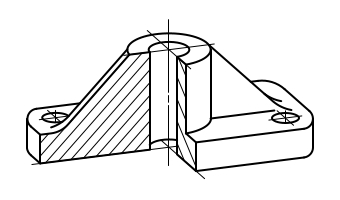
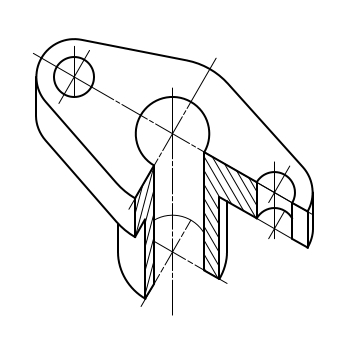
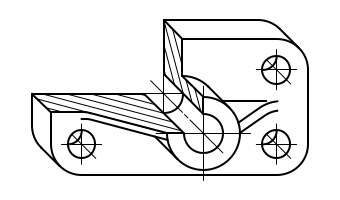
Последовательность изображения детали в аксонометрии представлена на рис. 5.7. Сначала на ортогональном чертеже детали выполняем разрезы и определяем положение координатных осей. При изображении аксонометрии симметричных тел целесообразно одну из осей ( в данном случае ось Z) совместить с осью тела.

Первым этапом построения аксонометрической проекции детали проводим аксонометрические оси и делаем разметку всех центров отверстий, отмечая их аксонометрическими осями.

Второй этап состоит в изображений фигур сечений, получаемых при мысленном рассечении тела плоскостями параллельными П₁, П₂, П₃. Выполняем штриховку сечений соответственно направлениям представленным на рис. 5.7. В прямоугольной диметрии коэффициент искажения по оси Y равен 0,5 и штриховка выполняется с учетом этого. Следует отметить, что условность , применяемая на чертежах по ГОСТ 2.305-68 относительно сплошных тонких тел, называемых ребрами жесткости, круглых непустотелых валов и т.п., на аксонометрические проекции не распространяются. Эти элементы в аксонометрии показываются рассеченными и заштриховываются.

Третий этапсостоит в построении линий пересеения поверхностей тела, лежащих за секущими плоскостями.

Четвертый этапдополняет построение поверхностей деталей, лежащих за фигурами сечений.

Пятый этап завершаем построение аксонометрического изображения детали , выполняя его обводку сплошной основной линией по ГОСТ 2.303-68, толщиной от 0,6 до 1,5 мм.

По завершении построений с чертежа убираются все линии построения, оставляя обязательно аксонометрические оси для всех поверхностей вращения детали.

Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Аксонометрические проекции

Для того чтобы наиболее наглядно передать форму изделий и предметов, ясно и понятно представить схемы взаимодействия различных деталей, по мере надобности применяются аксонометрические проекции.

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Прямоугольная изометрическая проекция

Проекция этого вида отличается тем, что в ней оси аксонометрии располагаются друг по отношению к другу под углом 120°. При этом искажения изображения по всем аксонометрическим осям имеют один и тот же коэффициент, равный 0,82.

Чтобы упростить изометрическую проекцию, по осям x, y и z, как правило, выполняют без искажений, то есть его коэффициент выбирают равным единице.

Видео:2 2 3 построение изометрии окружностиСкачать

Изображение окружностей в прямоугольной изометрии

Если окружности располагаются в тех плоскостях, которые параллельны плоскостям проекций, то в аксонометрической плоскости они изображаются в виде эллипсов.

В тех случаях, когда по осям x, y, и z изометрическая проекция выполняется без искажений, длина большой и малой осей эллипсов составляет, соответственно, 1,22 и 0,71 от диаметра отображаемой окружности.

В тех случаях, когда по осям x, y и z изометрическая проекция выполняется с искажениями, длина большой оси эллипсов равняется диаметру отображаемой окружности, а длина малой оси – 0,58 от нее.

Видео:Изображение окружности в перспективе. Эллипс.Скачать

Изображение детали в прямоугольной изометрии

Чтобы наиболее наглядно передать особенности формы различных изделий и предметов, их изображают в прямоугольной изометрической проекции.

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Прямоугольная диметрическая проекция

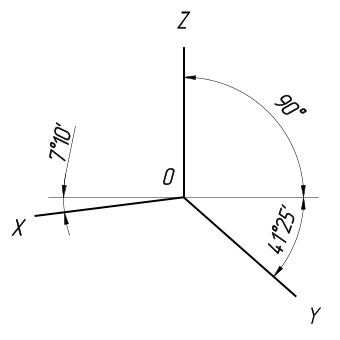
Отличительной особенностью прямоугольной диметрической проекции является то, что она имеет различные коэффициенты искажения по разным аксонометрическим осям: для x и z он имеет значение 0,94, а по y, равна значению 0,47.

В большинстве случаев диметрическая проекция выполняется с коэффициентом искажения по оси аксонометрии y, равным 0,5, и по осям аксонометрии z и x, равным единице.

Видео:Как начертить овал во фронтальной плоскостиСкачать

Изображение окружностей в прямоугольной диметрии

Те окружности, которые располагаются в плоскостях, являющихся параллельными по отношению к плоскости проекции, при проецировании на аксонометрическую плоскость изображаются в виде эллипсов.

В тех случаях, когда диметрическая проекция окружности выполняется в неискаженном виде по осям z и x, длина большой оси эллипсов составляет 1,06 от диаметра изображаемой окружности, при этом малая ось эллипса под номером 1 ровна 0,95, а эллипсов под номерами 2 и 3 ровна 0,35 диаметра окружности.

В тех случаях, когда диметрическая проекция окружности выполняется в искаженном виде по осям x и z, длина больших осей всех эллипсов соответствует диаметру окружности, малой оси эллипса под номером 1 равна 0,9, а эллипсов с номерами 2 и 3 равна 0,33 длины диаметров окружности.

Видео:Изображение в изометрической проекции окружностей, вписанных в кубСкачать

Изображение детали в прямоугольной диметрии

Для того чтобы в печатных изданиях и на некоторых других видах носителей информации представить деталь или изделие наиболее наглядно, ее изображают в прямоугольной диметрии.

Видео:Построение прямоугольной изометрии окружностиСкачать

Косоугольная фронтальная изометрическая проекция

Для этой проекции характерно то, что проекции с углом наклона оси у допускается располагать с углом наклона от 30° до 60°. Фронтальная изометрическая проекция по осям x, y и z искажений не имеет.

Видео:Прямоугольные диметрические проекцииСкачать

Изображения окружности в косоугольной фронтальной изометрии

Те окружности, которые располагаются в плоскостях, лежащих параллельно фронтальной плоскости проекций, на аксонометрическую плоскость проецируются в виде окружностей. Те окружности, которые располагаются в плоскостях, находящихся параллельно профильной и горизонтальной плоскостям проекций, проецируются в эллипсы. При этом длина их больших осей составляет 1,3 диаметра окружности, а малой оси – 0,54 диаметра окружности.

Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Изображение детали в косоугольной фронтальной изометрии

Изображение деталей в косоугольной фронтальной изометрии, используется для того, чтобы наиболее наглядно передать форму изделий и предметов.

Видео:Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Косоугольная горизонтальная изометрическая проекция

Отличительной особенностью косоугольной горизонтальной изометрической проекции является то, что здесь допускается применять, что проекции с углом наклона оси у допускается располагать под углом наклона от 45° до 60°, при этом угол 90° между осями x и y должен сохраняться неизменным. В данной проекции искажения отсутствуют по всем осям.

Видео:Построение аксонометрии моделиСкачать

Изображения окружности в косоугольной горизонтальной изометрической проекции

Те окружности, которые располагаются в плоскостях, находящихся параллельно горизонтальной плоскости проекций, на аксонометрическую плоскость проецируются в окружности. Те окружности, которые располагаются в плоскостях, находящихся параллельно профильной и фронтальной плоскостям проекций, проецируются в эллипсы.

Наибольшая ось эллипса под номером 1 равна 1,37, а малая ось равна 0,37 от диаметра окружности. Большая ось эллипса номер 3 равна 1,22, а малая ось равна 0,71 от диаметра окружности.

Видео:1 2 4 сопряжение окружностейСкачать

Изображение детали в косоугольной горизонтальной изометрии

Эта проекция используется для того, чтобы наиболее наглядно передать форму изделий и предметов.

Видео:2 2 1 изометрия по чертежуСкачать

Косоугольная фронтальная диметрическая проекция

Отличительной чертой этой проекции является то, что аксометрическая ось y может иметь угол наклона от 30° до 60°. При этом коэффициент искажения по осям x и z равняется единице, а по оси y – 0,5.

Видео:Как начертить овал в горизонтальной плоскостиСкачать

Изображения окружности в косоугольной фронтальной диметрии

Те окружности, которые располагаются в плоскостях, находящихся параллельно фронтальной плоскости проекций, на аксонометрическую плоскость проецируются в окружности. Те окружности, которые располагаются в плоскостях, находящихся параллельно профильной и горизонтальной плоскостям проекций, проецируются в эллипсы. При этом длина их больших осей составляет 1,07 диаметра окружности, а малой оси – 0,33 диаметра окружности.

Видео:Часть 1. Изометрическая проекция. (стр. 29)Скачать

Изображение детали в косоугольной фронтальной диметрии

Эта проекция используется для того, чтобы наиболее наглядно передать форму изделий и предметов.

Видео:Окружности в изометрических проекциях.Скачать

Нанесение размеров

Размерные линии при изображении аксонометрических проекций должны наноситься параллельно измеряемым отрезкам, а выносные – параллельно аксонометрическим осям.

Видео:Шестиугольник в изометрииСкачать

Штриховка

Сечения во всех аксонометрических проекциях наносится штриховкой. При этом ее линии должны быть параллельны лежащим в соответствующих координатных плоскостях диагоналям проекций квадратов.

📽️ Видео

Построение окружности в изометрии.Скачать