Презентация на тему числовая окружность на координатной плоскости (3 видео)

Числовая окружность в координатной плоскости
презентация к уроку по алгебре (10 класс) на тему

Содержание

Презентация к уроку математики 10 класса: Числовая окружность в координатной плоскости
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Презентация «Числовая окружность на координатной плоскости» 10 класс
Презентация «Числовая окружность на координатной плоскости»
🎦 Видео

Презентация к уроку математики 10 класса: Числовая окружность в координатной плоскости

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Скачать:

Вложение	Размер
05._chislovaya_okruzhnost_v_koordinatnoy_ploskosti.pptx	1.93 МБ

Предварительный просмотр:

Видео:Числовая окружность на координатной плоскости | Алгебра 10 класс #10 | ИнфоурокСкачать

Подписи к слайдам:

Числовая окружность в координатной плоскости

Повторим: Единичная окружность – числовая окружность, радиус которой равен 1. R=1 C=2 π + — у х

Если точка М числовой окружности соответст-вует числу t, то она соответствует и числу вида t+2 π k , где k – любое целое число (k ϵ Z) . M(t) = M(t+2 π k), где k ϵ Z

Основные макеты Первый макет 0 π у х Второй макет у х

х у 1 А(1, 0) B ( 0 , 1 ) C ( — 1, 0) D ( 0 , -1 ) 0 x>0 y>0 x 0 x 0 y Мне нравится

Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Презентация «Числовая окружность на координатной плоскости» 10 класс

Код для использования на сайте:

Скопируйте этот код и вставьте себе на сайт

Для скачивания поделитесь материалом в соцсетях

После того как вы поделитесь материалом внизу появится ссылка для скачивания.

Подписи к слайдам:

Муниципальное общеобразовательное учреждение средняя общеобразовательная школа № 1

по алгебре и началам анализа

Числовая окружность на

Преподавание предмета ведется по блочно- модульной технологии.

Данный урок один из уроков изучения нового материала. Поэтому основное время урока отводится именно на изучение нового материала, причем большую часть этой работы ученики выполняют самостоятельно.

Виды деятельности учащихся на уроке: фронтальная, самостоятельная и индивидуальная работы.

Так как на уроке необходимо проделать большую по объему работу и обязательно проконтролировать результаты ученической деятельности, используется интерактивная доска на этапах актуализации знаний и изучения нового материала. Для более наглядного представления наложения числовой окружности на координатную плоскость и для рефлексии содержания учебного материала в конце учебного занятия используются и презентации Power Point.

Учить самостоятельно добывать знания

Воспитывать собранность, ответственность, усердие

Учить анализировать, сравнивать, строить аналогии

1) Организационный момент, тема, цель урока 2 мин.

2) Актуализация знаний 4 мин.

3) Изучение нового материала 30 мин.

4) Рефлексия 3 мин.

5) Итог урока 1 мин.

рассмотреть числовую окружность на координатной плоскости; вместе найти координаты двух точек; далее самостоятельно составить таблицы значений координат других основных точек окружности;

проверить умение находить координаты точек числовой окружности.

В курсе геометрии 9 класса изучали следующий

На единичной полуокружности (R = 1) рассмотрели точку М с координатами х и у

Выдержки из учебника геометрии

Научившись находить координаты точки единичной окружности,

с легкостью перейдём к их другим названиям: синусам и косинусам, т.е.

к основной теме- ТРИГОНОМЕТРИЯ

Первое задание дано на интерактивной доске, где учащимся необходимо расставить точки и соответствующие им числа по местам на числовой окружности, перетащив их пальцем по доске.

Второе задание дано на интерактивной доске. Ответы закрыты «шторой», открываются по мере решения.

Итог выполнения задания:

Изучение нового материала

Возьмём систему координат и на неё наложим числовую окружность так, чтобы их центры совпали, а горизонтальный радиус окружности совпал с положительным направлением оси ОХ (презентация Power Point)

В результате имеем точки, которые принадлежат одновременно числовой окружности и координатной плоскости. Рассмотрим одну из таких точек, например, точку М (презентация Power Point)

Видео:Числовая окружность на координатной плоскостиСкачать

Презентация «Числовая окружность на координатной плоскости»

Документы в архиве:

Название документа 10. Числовая окружность на координатной плоскости.ppt

Описание презентации по отдельным слайдам:

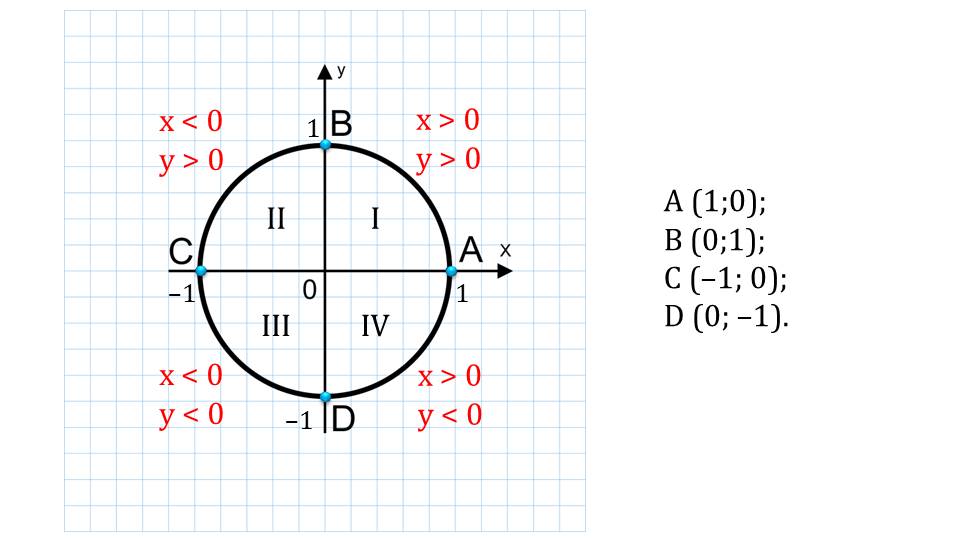
I II III IV 1 1 –1 –1 А (1;0); В (0;1); С (–1; 0); D (0; –1). x > 0 y > 0 x 0 x 0 y № слайда 3

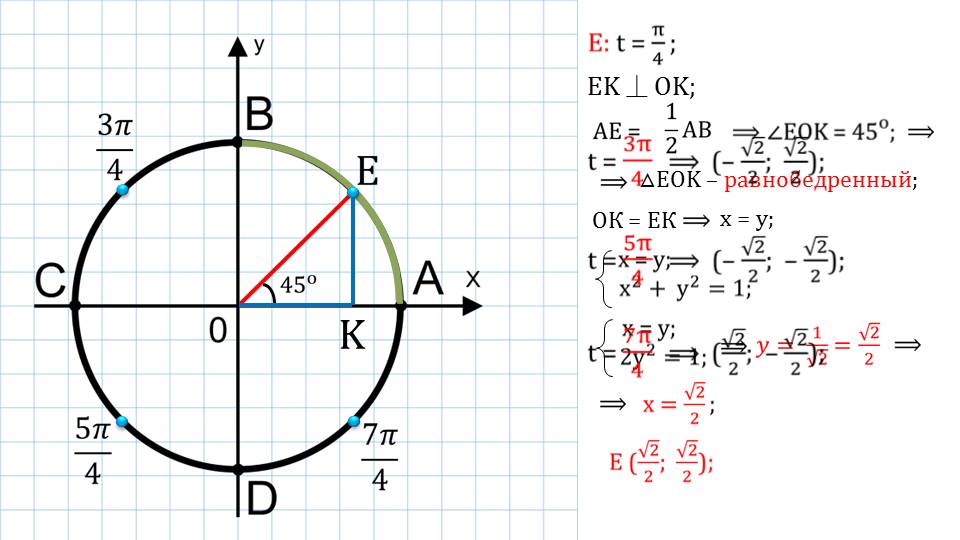
E (x;y) – точка окружности; –1≤ х ≤ 1; –1≤ у ≤1; уравнение окружности: х2 + у2 =R2;

K EK ⏊ OK; △EOK – равнобедренный; ОК = ЕК x = y;

DP ⏊ OK; P ОD = OA = 1; По теореме Пифагора: ОР 2 = ОD2 – DР2 ОР = х, x > 0,

Если точка D числовой окружности соответствуют числу t, то она соответствует и любому числу вида t + 2πk, где k ϵ Z.

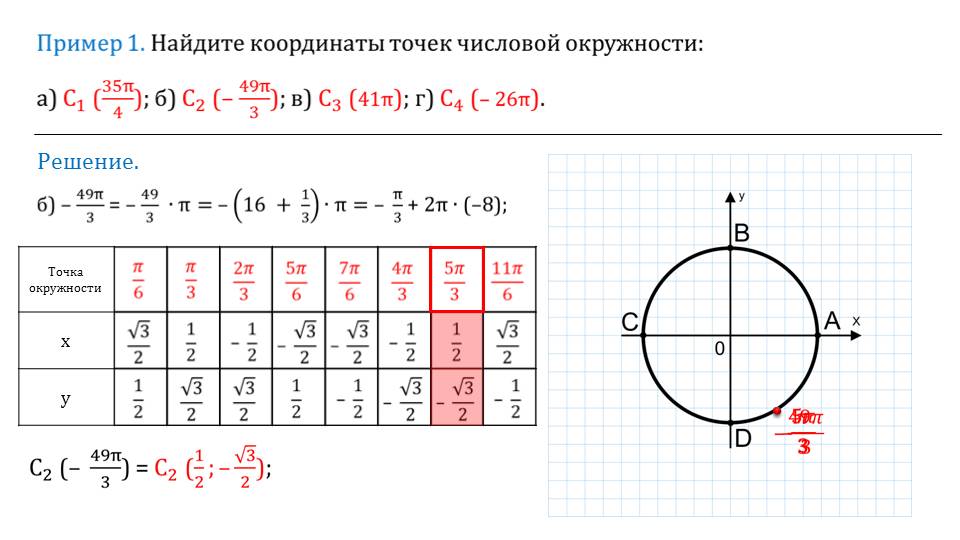
Решение. в) 41π = 40π + π = π + 2π ∙ 20; г) – 26π = 0 + 2π ∙ ( – 13); С4( – 26π)= С4(1; 0).

Краткое описание документа:

Данная презентация поможет десятиклассникам при изучении одной из тем касательно числовой окружности.

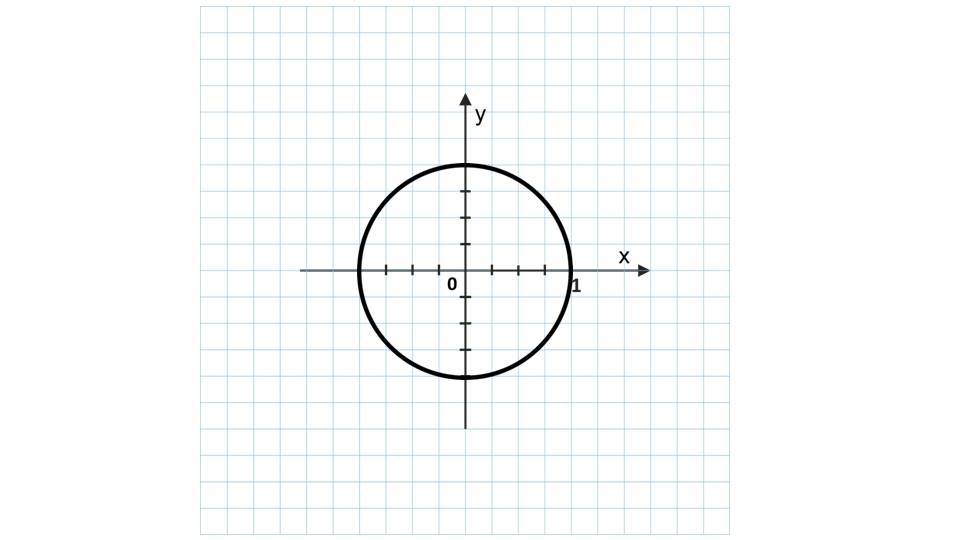
Речь идет о рассмотрении числовой окружности на координатной плоскости.

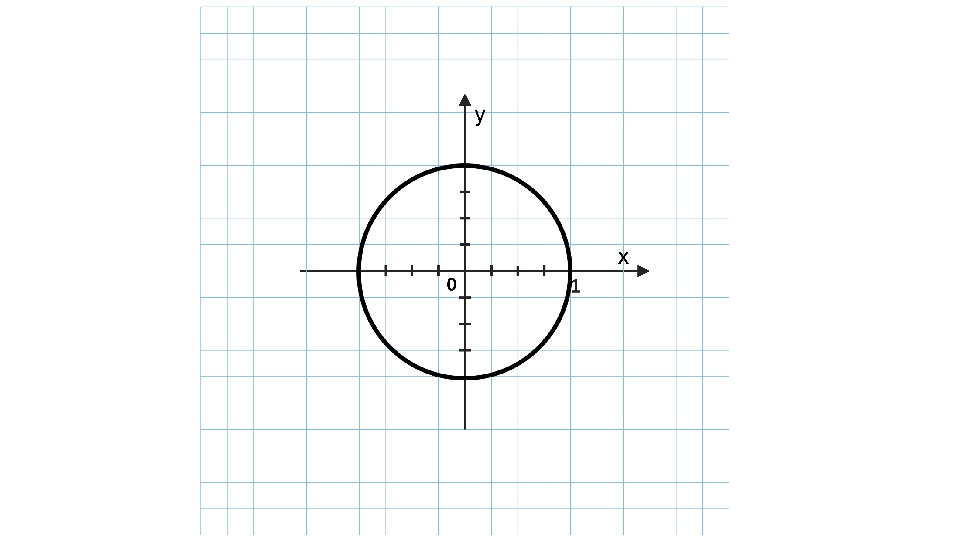
На первом слайде демонстрируется координатная плоскость, на которой изображается окружность. Мы видим, что центр окружности в начале координат, а радиус равняет единице. Это говорит о том, что данная окружность является единичной.

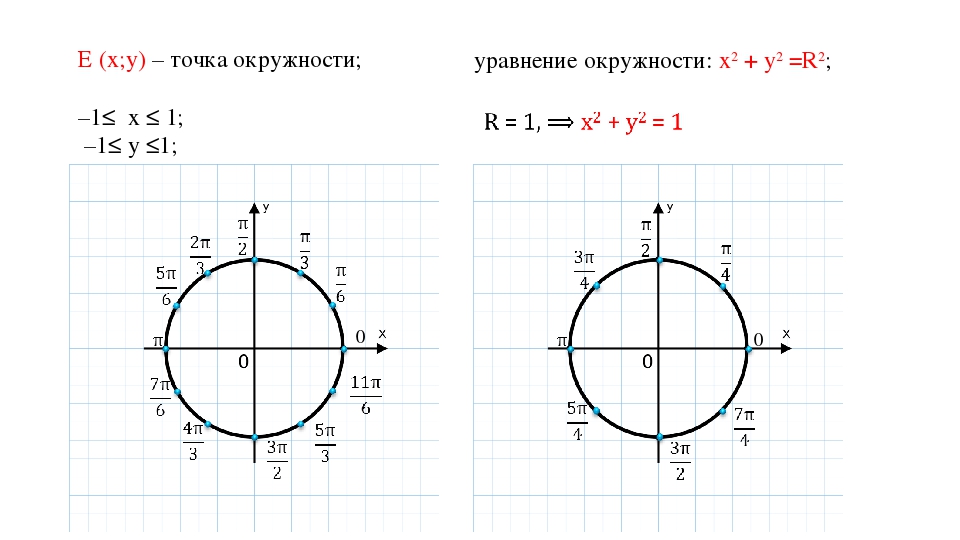
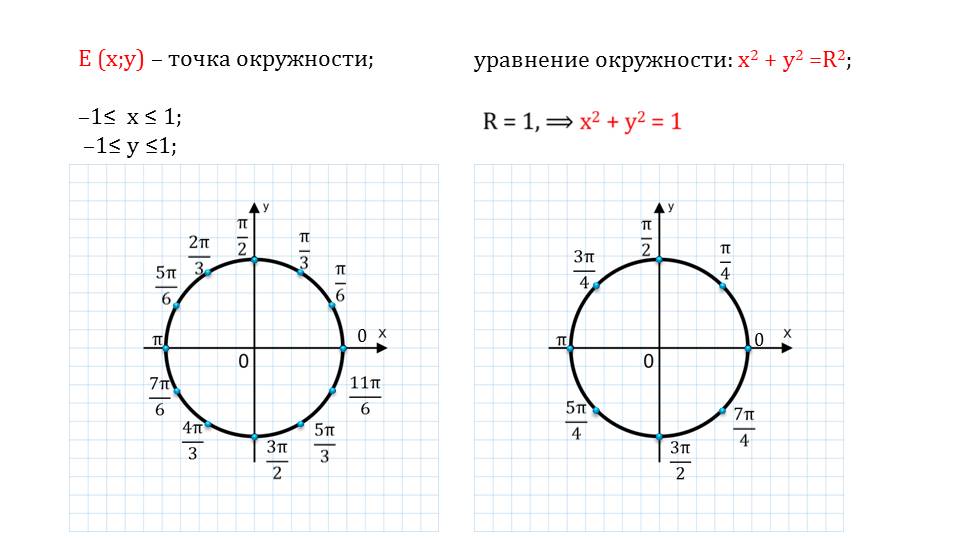
Следующий слайд демонстрирует этот же рисунок, с более подробным его описанием. Мы видим, что обозначены точки пересечения окружности с осями координат, которые разбивают ее на 4 дуги. Также обозначены четверти римскими цифрами, как это принято в большинстве источников.

С правой стороны от рисунка показаны координаты каждой точки пересечения окружности с осями ОХ и ОУ. Также расписаны значения х-ов и у-ов на той или иной четверти.

На следующем слайде приводится общий вид обозначения произвольной точки на окружности. Приводит функция, построив которую мы получим окружность. С правой стороны уравнения данной функции стоит радиус ее в окружности. Мы ведь знаем, чему равняется радиус единичной окружности – единице.

Подставив данное значение, мы и получим уравнение единичной окружности. С левой стороны на данном слайде можно увидеть, что отмечается очень важный и очевидный факт: х-ы и у-ы ограничены интервалом [-1; 1].

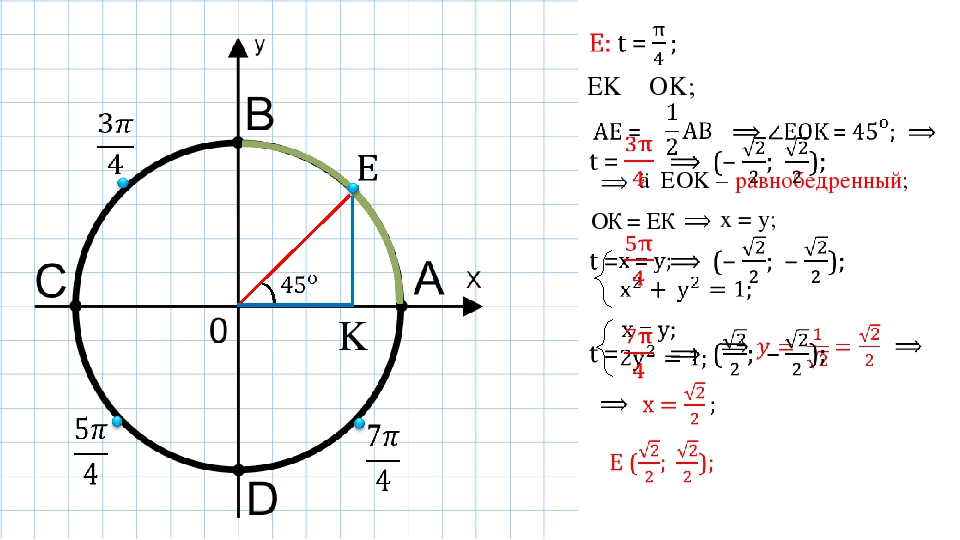
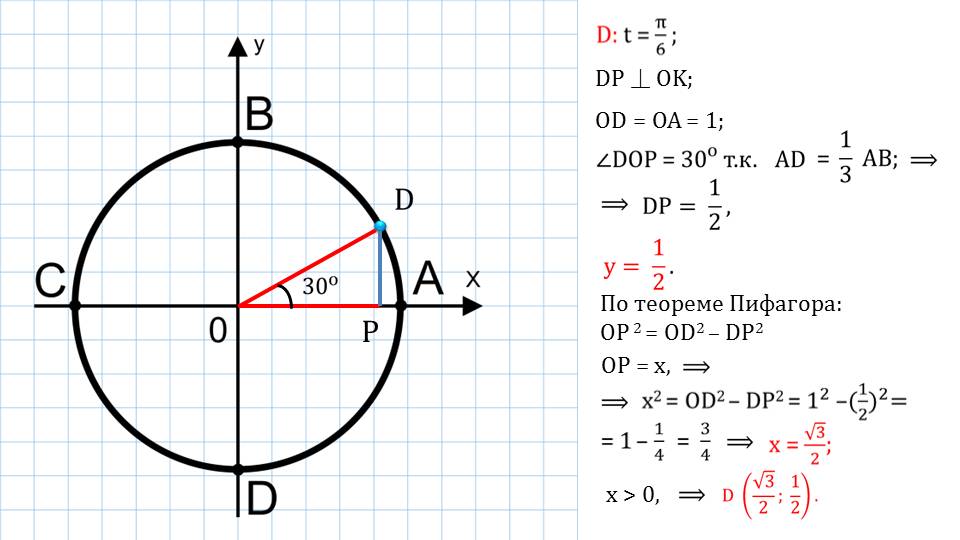
Если выбрать любую точку на окружности, то можно построить прямоугольный треугольник.

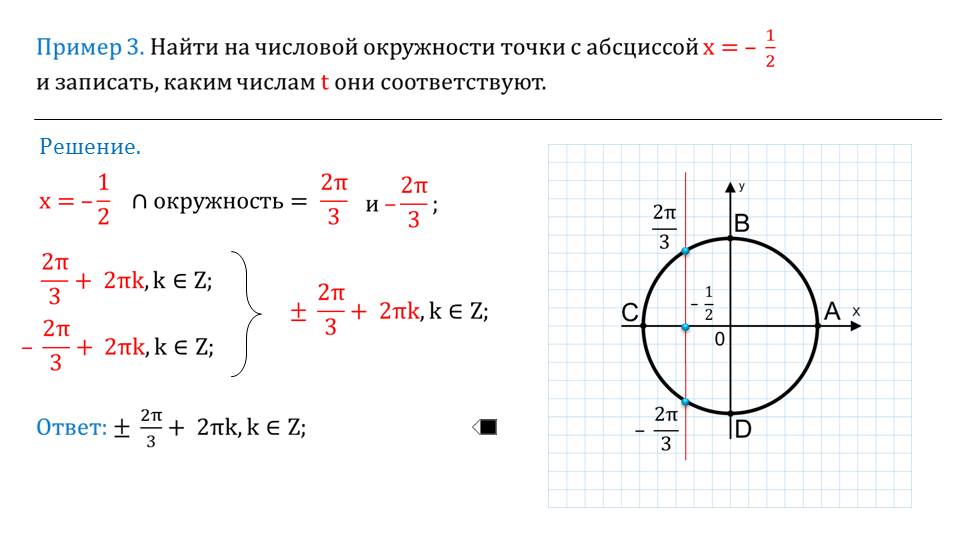
Для этого необходимо соединить две точки – выбранную точку на окружности и началом координат. Третью точку можно получить при проведении от выбранной точки к оси ОХ перпендикуляр.

Подробным образом демонстрируется, как с использованием значения угла и знания о дуге окружности можно найти координаты той или иной точки на окружности.

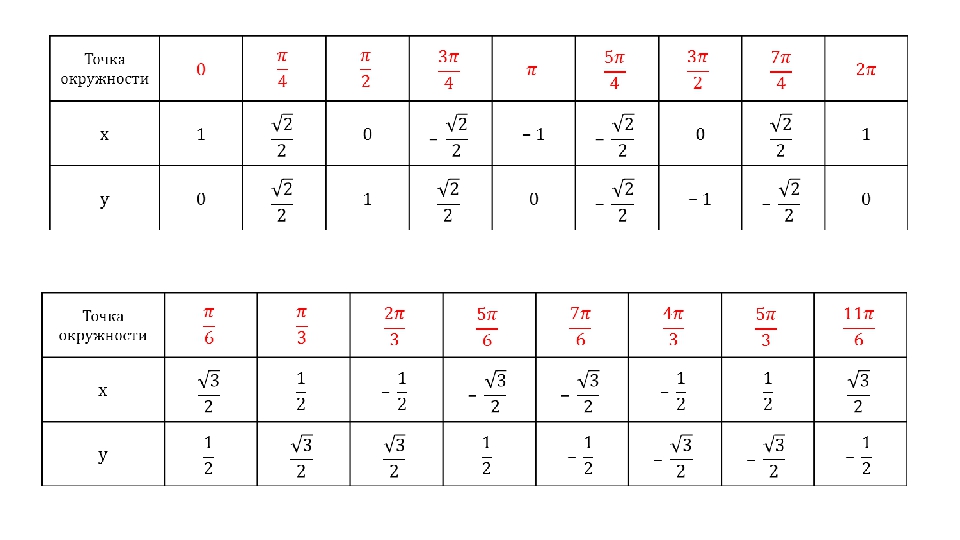
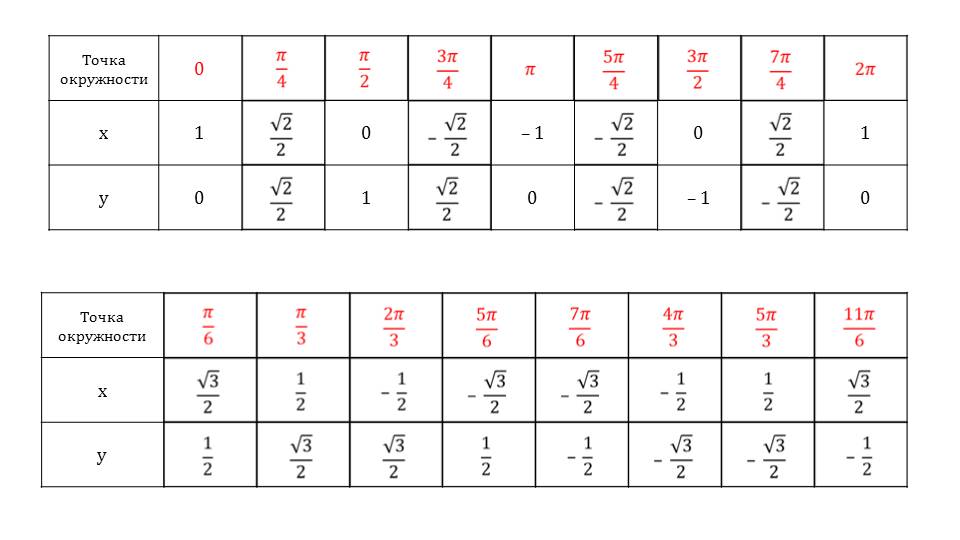
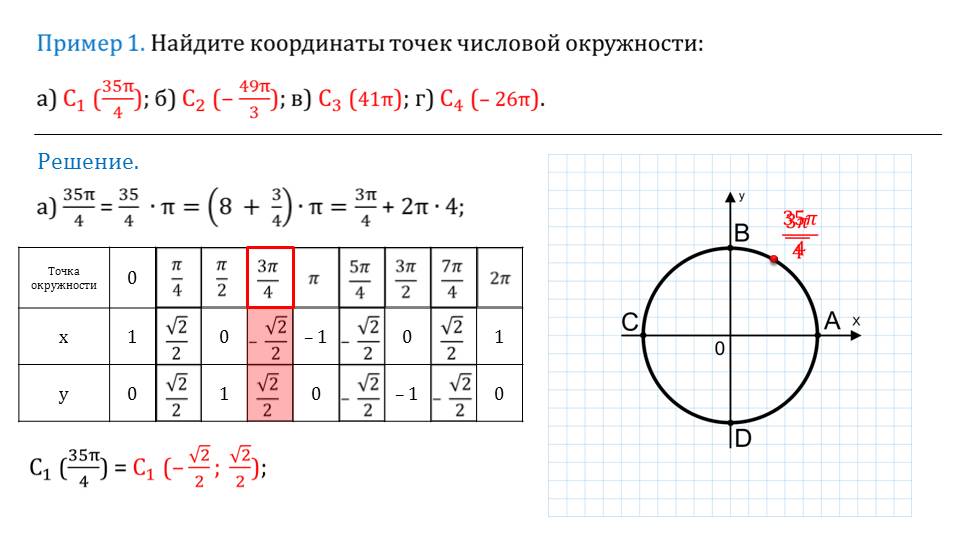
Приводится таблица, с готовыми расчетами, которую можно использовать при решении различных задач. Чтобы правильно ею пользоваться, рассматриваются примеры.