Правильный треугольник 60 градусов

Калмыцкий государственный университет

NovaInfo32
Опубликовано 13 марта 2015
Раздел: Физико-математические науки
Просмотров за месяц: 553
CC BY-NC

Видео:Геометрия Равносторонний треугольникСкачать

Аннотация

Треугольник с углом 60 градусов обладает необычными свойствами. Если этот треугольник не является правильным, то все три угла всегда образуют арифметическую прогрессию. Выполняется и обратное утверждение: Если сумма углов треугольника образует арифметическую прогрессию, то один из углов равен 60 градусам. Кроме того, между треугольниками с углами 45, 60, 75 и 30, 60, 90 градусов существует сложная взаимность.

Видео:№551. Осевое сечение конуса — правильный треугольник со стороной 2г. Найдите площадь сечения,Скачать

Ключевые слова

Видео:Построить угол 60°Скачать

Текст научной работы

Докажем свойство треугольника с углом 60 градусов.

Теорема. Если треугольник с углом 60 градусов не является правильным, то его углы составляют арифметическую прогрессию.

Пусть в треугольнике ABC угол B равен 60 о , а угол A=α (рис.1). Так как сумма углов треугольника равна 180 о , то ÐA+ÐC=120 o . Тогда, ÐС=120 o −α.

Таким образом, ÐA=α, ÐB=60 o =α+(60 o −α), ÐC=120 o −α=α+2(60 o −α) (1)

Из соотношения (1) видно, что углы треугольника составляют арифметическую прогрессию с разностью 60 o −α. Теорема доказана.

Справедливо и обратное утверждение.

Теорема. Если углы треугольника составляют арифметическую прогрессию, то один из углов равен 60 о .

Пусть ÐA=α, ÐB=α+d, ÐC=α+2d (рис.2). Сумма углов треугольника равна 180 о , поэтому α+α+d+α+2d=180 o =>3α+3d=180 o =>α+d=60 o =>d=60 o −α.

Отсюда ÐB=α+60 o −α=60 o . Теорема доказана.

Существуют и другие необычные свойства треугольников с углами 60 о .

Для треугольника 45 о , 60 о , 75 о ортоцентрическим является треугольник с углами 30 о , 60 о , 90 о . Если продолжить высоты треугольника до их пересечения с описанной окружностью, то получим треугольник подобный высотному (рис.3).

Рисунок 3. Высотный треугольник и ему подобный

Назовём инцентрическим треугольник, образованный основаниями перпендикуляров опущенных из центра вписанной окружности на стороны. Для треугольника с углами 30 о , 60 о , 90 о инцентрическим будет треугольник с углами 45 о , 60 о , 75 о (рис.4).

Рисунок 4. Инцентрический треугольник

Видео:№225. Докажите, что каждый угол равностороннего треугольника равен 60°.Скачать

Читайте также

Средства стохастической подготовки обучающихся на основе информационных технологий

Инструментальная реализация прикладной математической подготовки бакалавра экономики и менеджмента

1. Синчуков А.В.

NovaInfo59, с.24-28, 13 февраля 2017 , Физико-математические науки, CC BY-NC

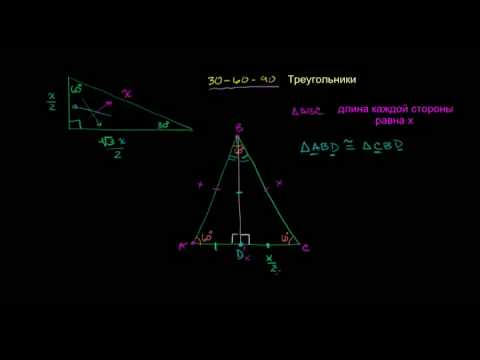
Видео:Соотношение сторон треугольника 30-60-90 (доказательство)Скачать

Список литературы

1. Алгебра. 9 класс : учеб. для общеобразоват. организаций [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова] ; под ред. С. А. Теляковского. – 21-е изд. – М.: Просвещение, 2014. – 271 с.: ил.
2. Геометрия: учеб. для 7-9 кл. сред. шк. /Л. С. Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 1990. – 336 с.

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Цитировать

Баталаев, А.В. Особые свойства треугольника с углом 60 градусов / А.В. Баталаев. — Текст : электронный // NovaInfo, 2015. — № 32. — URL: https://novainfo.ru/article/3266 (дата обращения: 31.01.2022).

Видео:№1083. Сколько сторон имеет правильный многоугольник, если каждый его угол равен: а) 60Скачать

Поделиться

Электронное периодическое издание зарегистрировано в Федеральной службе по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор), свидетельство о регистрации СМИ — ЭЛ № ФС77-41429 от 23.07.2010 г.

Соучредители СМИ: Долганов А.А., Майоров Е.В.

Видео:38 Чевианы правильного треугольника, пересекающиеся под углом величиной 60 градусовСкачать

Как начертить равносторонний треугольник

Из этого материала вы узнаете, как с помощью циркуля построить правильный треугольник. Напомним, что треугольник является правильным, если длина всех его сторон одинакова, а каждый из углов составляет 60°.

На листе бумаги отметьте произвольную точку. Установите в эту точку иглу циркуля и нарисуйте окружность.

Установите иглу циркуля в любую произвольную точку, лежащую на окружности, и нарисуйте вторую окружность с центром в этой точке.

При этом не меняйте раствор циркуля, то есть радиус первой окружности должен быть равен радиусу второй окружности.

Отметьте точки пересечения окружностей.

Соедините полученные точки линией. Полученный отрезок будет первой стороной треугольника.

Далее, через центры обеих окружностей нужно провести прямую линию.

Таким образом, у вас получилось три точки, которые будут тремя вершинами треугольника.

Соедините все три точки между собой.

Полученный треугольник имеет одинаковую длину сторон, а величина каждого его угла составляет 60°, а значит он правильный.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Правильный треугольник

Средняя оценка: 4.6

Всего получено оценок: 79.

Средняя оценка: 4.6

Всего получено оценок: 79.

Правильный треугольник имеет много специфических свойств, которые значительно упрощают решение задач. Поэтому имеет смысл поговорить о каждом из этих свойств, дабы облегчить решение задач.

Видео:Найдите угол: задача по геометрииСкачать

Определение

Правильный треугольник – это треугольник, у которого все стороны равны и каждый угол равен 60 градусам. Правильный треугольник еще называют равносторонним. О формулах правильного треугольника, и о том, как производить по ним различные вычисления – поговорим ниже.

Рис. 1. Правильный треугольник.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Формулы правильного треугольника

Почти все формулы вытекают из утверждения о том, что правильный треугольник имеет 3 угла по 60 градусов и 3 одинаковые стороны.

Площадь

Начнем с формулы площади.

Равносторонний треугольник любой высотой делится на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для нахождения площади правильного треугольника.

Рис. 2. Рисунок к доказательству.

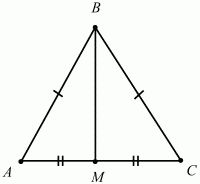
В прямоугольном треугольнике АВМ катет ВМ можно выразить через синус угла ВАМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет ВМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.

С другой стороны синус 60 градусов заранее известнее и равен $sqrt over 2$ . Значит можно выразить значение АМ:

Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.

Тогда формула будет выглядеть следующим образом:

Теперь вспомним классическую формулу площади треугольника:

$S= h*a$, где а это основание треугольника, h – высота, проведенная к этому основанию. В заданном треугольнике это будет выглядеть следующим образом:

Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.

Только в правильном треугольнике возможно нахождение площади через значение одной стороны.

Периметр

Периметр найти ещё проще, так как это сумма всех сторон треугольника, а они все равны между собой, то:

Подобный подход, где приравниваются стороны или используются свойства медиан и биссектрис равностороннего треугольника, часто используется при решении подобных задач. У правильного треугольника нет и не может объема, так как это плоская фигура. У нее два характеризующих понятия: площадь и периметр.

В равностороннем треугольнике каждая биссектриса совпадает с медианой и высотой. Также совпадают и точки пересечения этих отрезков. Получившаяся точка зовется центром фигуры.

Видео:Найдите УГОЛ. Находим угол шестиугольной полки.Скачать

Что мы узнали?

Из статьи мы узнали, что у правильного треугольника все стороны и углы равны между собой. Мы узнали о свойствах биссектрисы, медианы и высоты – в правильном треугольнике это будет одна и та же линия. Ее можно проводить от любой вершины.

🎬 Видео

Геометрия Синус.Чему равен синус 30,45,60 градусов?Вывод табличных значений.Скачать

Формулы равностороннего треугольника #shortsСкачать

Построение угла с помощью транспортира. 5 клСкачать

Классный способ для разметки любого угла без транспортира.Скачать

Тригонометрия: значения синуса, косинуса и тангенса для углов 30, 45 и 60 градусовСкачать

Найдите угол между сторонами квадрата внутри правильного треугольникаСкачать

7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать