Поворот окружности вокруг точки

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №29. Радианная мера угла

Перечень вопросов, рассматриваемых в теме:

1) Понятие тригонометрической окружности;

2) Поворот точки вокруг начала координат;

3) Длина дуги окружности и площадь кругового сектора.

Глоссарий по теме

Окружность – это замкнутая линия, все точки которой равноудалены от центра.

Радиус окружности – отрезок, соединяющий её центр с любой лежащей на окружности точкой.

Круг – часть плоскости, ограниченная окружностью.

Дуга окружности – кривая линия, лежащая на окружности и ограниченная двумя точками.

Круговой сектор – часть круга, ограниченная двумя радиусами.

Угол в 1 радиан – центральный угол, опирающийся на дугу, равную по длине радиусу окружности.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Теоретический материал для самостоятельного изучения

На уроках геометрии мы с вами изучали окружность, её элементы, свойства. Повторим понятие окружности. Это замкнутая линия, все точки которой равноудалены от центра.

Радиусом окружности называется отрезок, соединяющий её центр с любой лежащей на окружности точкой.

На окружности можно выделить дугу. А если рассмотреть круг — часть плоскости, ограниченной окружностью — то можно выделить круговой сектор.

«Окружность бесконечно большого круга и прямая линия – одно и то же» Г. Галилей

Действительно, и окружность и прямая – бесконечны. Рассмотрим окружность радиуса, равному 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют единичной или тригонометрической. (рис.1)

Длина этой окружности (в предыдущей задаче велотрека), как мы помним из уроков геометрии, . А учитывая, что R=1, , осями координат она поделена на четыре дуги, которые находятся соответственно в I, II, III и IV координатных четвертях.

Вычислите длину каждой дуги.

Ответ. длина каждой дуги равна части окружности или

Длина полуокружности равна А так как образовался развернутый угол, то 180.

Рассмотрим дугу, равную по длине радиусу единичной окружности. Полученный центральный угол РОМ равен длине дуги МР=R.

рис.3

Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.

;

α рад=(180/π α)° (1)

Длину дуги l окружности радиуса R (рис.4)

можно вычислять по формуле(3)

А площадь S кругового сектора радиуса R и дугой рад (рис.5)

находят по формуле: , где (4)

Вернёмся к единичной окружности в координатной плоскости.

Каждая точка этой окружности будет иметь координаты х и у такие, что выполняются неравенства -1≤ х ≤ 1; -1≤ у ≤ 1.

Введём понятие поворота точки. (рис.2)

1. Пусть Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
2. Пусть точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол — α.

При повороте на 0 рад точка остаётся на месте.

Давайте рассмотрим такой пример:

при повороте точки М(1;0) на угол получается точка N (0;1). В эту же точку можно попасть из точки М(1;0) при повороте на

угол (рис.6)

Примеры и разбор решения заданий тренировочного модуля

Найти градусную меру угла, равного рад.

Решение: Используя формулу (1),

находим .

Так как , то рад, тогда (2)

Ответ: .

Пример 2. Найти радианную меру угла, равного 60.

Вычисляем по формуле (2): рад

рад

При обозначении мер угла, наименование «рад» опускают.

Ответ: рад, рад.

Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера .

Решение: Используя формулу (3),

получим:

Ответ: .

Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла .

По формуле (4) вычисляем

Ответ: 45 м 2

Пример 5. Найти координаты точки М, полученной из точки N(1;0) поворотом на угол, равный .

Решение: Абсцисса точки М равна отрезку ОК, ордината отрезку ОТ=МК. Так как то

прямоугольный равнобедренный треугольник ОМК имеет равные катеты и гипотенузу ОМ=R=1. По теореме Пифагора можно найти длины катетов. Они равны Учитывая, что точка М находится в I координатной четверти, её координаты положительны.

На окружности можно найти координаты любой точки.

Ответ:

Видео:Решение задач по теме "Поворот точки вокруг начала координат"Скачать

Угол поворота, угол произвольной величины

Среди множества терминов тригонометрии важным является понятие угла поворота. В данной статье рассмотрим поворот и все соответствующие ему определения; дадим представление о полном обороте; изучим угол поворота и его характеристики, а также поворот фигуры вокруг точки. Для лучшего понимания теория будет снабжена иллюстрациями и практическими примерами.

Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Поворот точки вокруг точки

Центр поворота – точка, относительно которой осуществлен поворот.

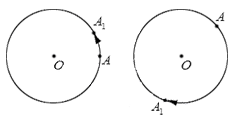
Рассмотрим, что происходит в результате поворота точки. Пусть некоторая точка А поворачивается относительно центра поворота О , в результате чего получается точка А 1 (при совершении некоторого количества полных оборотов она может совпасть с точкой А ). При этом точка А 1 лежит на окружности с центром в точке О радиуса О А . Другими словами, когда точка А осуществляет поворот относительно точки О , она переходит в точку А 1 , лежащую на окружности с центром О радиуса О А .

Считается, что в данном случае точка О при осуществлении поворота вокруг самой себя переходит в саму себя. Или: когда точка О осуществляет поворот вокруг центра поворота О , она переходит в саму себя.

Отметим также, что поворот точки А относительно центра О нужно рассматривать, в том числе, как перемещение в результате движения точки А по окружности с центром в точке О радиуса О А .

Изобразим графически поворот точки А относительно точки О , перемещение точки А в точку А 1 отметим стрелкой:

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Полный оборот

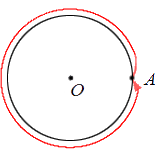
Возможно осуществить поворот точки А относительно центра поворота О таким образом, что точка А , пройдя все точки окружности, вернется на прежнее свое место. Тогда говорим, что точка совершила полный оборот вокруг точки О .

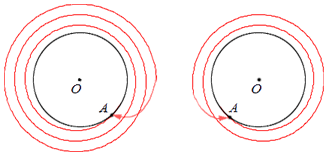
Если движение точки А по окружности продолжится, то будет выполнено два, три и так далее полных оборотов. На иллюстрации ниже справа отображено два полных оборота, а слева – три:

В рамках всего вышесказанного можно также говорить о частях полного оборота. Например, о половине оборота или трети, или четверти и так далее.

Видео:Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать

Угол поворота

Из указанного выше понятия поворота точки очевидно, что возможно бесконечное множество вариаций поворота точки А относительно центра О . Любую точку окружности с центром О можно рассматривать как точку А 1 , полученную в результате поворота точки А . Поэтому для определения отличия одного поворота от другого вводится понятие угла поворота.

Угол поворота имеет свои характеристики, одна из которых – направление поворота. По нему определяют, как перемещалась точка – по часовой стрелке или против.

Еще одной характеристикой угла поворота служит его величина. Углы поворота имеют ту же единицу измерения, что и углы в геометрии: наиболее распространены градусы и радианы. Отметим, что угол поворота может выражаться в градусах любым действительным числом в промежутке от — ∞ до + ∞ , что отличает его от угла в геометрии, который выражается только положительным числом, не превосходящим 180 ° .

Чтобы обозначить углы поворота, стандартно используют буквы греческого алфавита: α , β , γ и так далее. Чтобы обозначить большое количество углов поворота, применяют одну и ту же букву с различными нижними индексами: α 1 , α 2 , α 3 … . . α n .

Разберем характеристики угла поворота подробнее.

Видео:поворот точки вокруг начала координат 10 класс алгебра и анализСкачать

Направление поворота

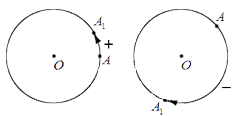
Отметим на окружности с центром О точки А и А 1 . В точку А 1 возможно попасть, совершив точкой А поворот относительно центра О либо по часовой стрелке, либо – против. Очевидно определять эти повороты, как различные.

Принято считать, что поворот по часовой стрелке – поворот в отрицательном направлении направлении, а поворот против часовой стрелки – поворот в положительном направлении.

Приведем графическую иллюстрацию различных поворотов: слева на чертеже – поворот в положительном направлении; справа – в отрицательном.

Видео:Поворот фигуры. Построить поворот фигур вокруг точки на угол по часовой или против часовой стрелкиСкачать

Величина угла поворота, угол произвольной величины

Угол поворота точки, не являющейся центром поворота, в полной мере определяется указанием его величины. С другой стороны, по величине угла поворота можно определить, каким образом поворот был осуществлен.

Как было сказано выше, величина угла поворота варьируется в пределах от — ∞ до + ∞ ;

Знак плюс определяет поворот против часовой стрелки, а минус – по часовой стрелке.

Необходимо установить соответствие между самой величиной угла поворота и тем, какому повороту она соответствует.

Пусть угол поворота равен 0 ° . Такому углу поворота соответствует перемещение точки в саму себя. Иначе говоря, при повороте вокруг точки О на 0 ° точка A остается на месте.

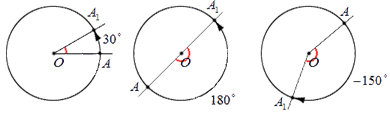
Теперь предположим, что поворот точки А происходит в пределах половины оборота: пусть точка А переходит в точку А 1 . В таком случае абсолютная величина угла А О А 1 , выраженная в градусах, не превосходит 180 . Если поворот имел положительное направление, то величина угла поворота считается равной величине угла А О А 1 ; если отрицательное – величина угла поворота равна величине угла А О А 1 со знаком минус. Для иллюстрации этих утверждений отобразим на чертеже углы поворота в 30 ° , 180 ° и — 150 ° :

Углы поворота, превышающие 180 или меньшие – 180 определяются, исходя из очевидного свойства последовательных поворотов:

Несколько последовательных поворотов точки А относительно центра О равносильны одному повороту, величина которого равна сумме величин этих поворотов.

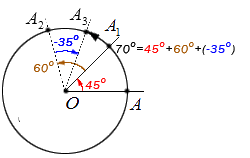
Рассмотрим пример, который даст нам возможность графически проиллюстрировать описанное свойство. Пусть точка А выполняет поворот относительно центра О на 45 ° , затем еще на 60 ° и еще раз — на — 35 ° . Обозначим промежуточные точки поворотов А 1 , А 2 и А 3 . В конечную точку А 3 возможно было попасть, совершив один поворот на угол поворота, величина которого равна: 45 ° + 60 ° + ( — 35 ° ) = 70 ° . Проиллюстрируем:

Таким, образом, углы, превышающие 180 ° , будем представлять, как несколько последовательных поворотов на углы, сумма величин которых определяет величину исходного угла поворота. Например, угол поворота 298 ° соответствует последовательным поворотам на 180 ° и 118 ° , или 90 ° , 90 ° , 90 ° и 28 ° , или 180 ° , 180 ° и — 62 ° , или 298 последовательных поворотов на 1 ° .

По такому же принципу определяются углы меньше — 180 ° . Например, угол поворота — 515 ° можно определить, как последовательные повороты на — 180 ° , — 180 ° и — 155 ° .

Нами был определен угол поворота, и его величина выражается в градусах некоторым действительным числом в пределах от — ∞ до + ∞ . Тригонометрия работает именно с углами поворота, хотя для удобства слово «поворот» опускают и говорят «угол». Т.е. будем рассматривать углы произвольной величины, понимая под ними углы поворота.

В заключение также отметим, что полный оборот в положительном направлении соответствует углу поворота в 360 ° или 2 π радиан. Соответственно при отрицательном направлении полный оборот будет соответствовать углу в — 360 ° или — 2 π радиан.

При этом удобно большие углы поворота представлять, как некоторое количество полных оборотов и еще один на величину в пределах от — 180 ° до 180 ° . К примеру, поворот осуществляется на 1478 ° . Представим эту величину как: 360 · 4 + 38 , т.е. заданному углу поворота соответствуют 4 полных оборота и еще один поворот – на 38 ° . Или еще один пример: угол поворота в — 815 ° можно представить, как ( — 360 ) · 2 + ( — 95 ) , т.е. заданному углу поворота соответствуют 2 полных оборота в отрицательном направлении (против часовой стрелки) и еще один поворот того же направления на — 95 ° .

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Поворот фигуры вокруг точки на угол

Понятие поворота точки легко распространить на поворот любой фигуры вокруг точки на угол (такой поворот, при котором и точка, относительно которой осуществляется поворот, и сама поворачиваемая фигура лежат в одной плоскости).

Поворот фигуры – это поворот всех ее точек вокруг заданной точки на заданный угол.

Как пример, иллюстрируем следующее действие: поворот отрезка А В на угол α относительно точки О – при повороте заданный отрезок перейдет в отрезок А 1 В 1 .

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

О матрице поворота простыми словами

Когда Пифагор плыл по реке Хуанхэ, он увидел у берега, в лодке, задремавшего рыбака, в конической шляпе и с бамбуковой удочкой в руках.

Памятуя о том, что на Хабрахабр заглядывают люди разной математической подготовки, — однако, в поле интересов которых вполне может попадать тема линейных преобразований, — в связи с её практической значимостью, — я попробую рассказать об этом максимально доступно.

Видео:Как искать точки на тригонометрической окружности.Скачать

Продолжим историю

Треугольные очертания лодки, шляпы и удочки над водой настолько поразили философа-математика, что он застыл как заворожённый.

Удочка рыбака аккуратно зависла над гладью вод Жёлтой Реки под углом, равным 45 градусам.

Лёгкий туман стелился над водой… и вдруг — поклёв. Рыбак потянул удочку, и она стала быстро набирать высоту, длина лески (катет А) стала расти на глазах, а расстояние от рыбака до самой лески стало уменьшаться (катет B). И самое интересное — длина самой удочки совсем не изменилась — телескопических удочек ещё не было, — даже когда она описала в воздухе дугу и оказалась почти над головой рыбака, под углом 90 градусов. Длина лески сравнялась с длиной удочки — катушки тогда уже были, — а расстояние между рыбаком и леской изменилось до 0, леска оказалась в руках рыбака.

Последний момент очень важен для понимания того, что происходит при умножении вектора-удочки на матрицу поворота.

Ностальгируем и думаем дальше.

Вспомним теорему Пифагора: квадрат длины удочки равен сумме квадратов катетов — самой лески и расстоянию между рыбаком и тем местом, где леска погружена в воду — С^2=А в квадрате + B в квадрате.

Представим, что длина удочки 4.2, длина (или высота над водой) лески 3, расстояние между рыбаком и местом, где леска погружена в воду тоже 3.

Видео:§22 Поворот точки вокруг начала координатСкачать

Окунёмся в поиски

1) найдём то, как соотносится между собой длина лески с длиной удочки — синус угла а.
2) найдём то, как соотносится длина отрезка между рыбаком и местом погружения лески с длиной удочки — косинус а. Считаем:

А теперь порассуждаем
Что будет если катет А разделить на sin(a)?! т.е.:

Получаем длину удочки — гипотенузу.
А если мы умножим катет А на sin(а)?!

Отметим это расстояние на гипотенузе — 2.1.

На оставшееся расстояние также приходится — 2.1, так как очевидно:

Это означает, то как в текущий момент времени синус и косинус делят гипотенузу. Поскольку квадрат гипотенузы это 4.2*4.2, то вопрос: что будет если 4.2 умножить на 2.1?! На ту самую её часть, с которой связан один из катетов:

Тоже самое для второго катета.

Нашли катеты. И убедились в том, что со времён Пифагора ничего не изменилось.

Видео:Радианная мера угла, поворот точки. Видеоурок 20. Алгебра 10 классСкачать

Далее

Теперь ещё раз осуществим умножение катета А на sin(a), катета B на cos(a).

Снова получили число равное длине удочки… и мы вплотную подобрались к матрице поворота.

Напомню формулу

Возьмём её нижнюю часть — получение точки y:

И сравним с вычислениями выше:

Как две капли воды. Y в нашем случае окажется равным 4.2.
Если применить первую часть формулы к вычислениям, то получим:

Иными словами случится так:

x станет 0 — рыбак поймает леску.
y станет 4.2 — леска сравняется с длиной удочки.

Помним, что для вычисления x синус и косинус меняются местами.

Ф в данном случае равно 45 градусам (Ф = 0.7 ) и при таком угле синус и косинус равны, что удобно для примера. В остальных случаях очевидно величины для синуса и косинуса будут другие. Например, для 40 градусов: cosdegree(40) = 0,7660444431, sindegree(40) = 0,6427876097 (если вы не согласны, обращайтесь в Яндекс, я пользовался его калькулятором).

Видео:9 класс, 33 урок, ПоворотСкачать

В итоге

Применяя формулу к новым значениям x,y несколько раз — в цикле, наглядно увидим движение по окружности, каждый раз на 45 градусов.

Если требуется сдвинуть вектор-удочку на один градус, то его и подставляем в формулу на место Ф.

Как происходит вычисление тригонометрических функций?!
Как известно, для вычисления косинуса и синуса угла обычно используются готовые функции. Согласно информации по ссылке вычисление и точность зависят от системы. Для unix-систем есть по крайней мере два варианта: функция, написанная в недрах компании IBM и встроенная инструкция fsin на Ассемблере. Есть также библиотека fdlibm с достаточно наглядным кодом и комментариями, по которым видно, что синус и косинус вычисляются в этой библиотеке через число pi.

Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

А вдруг автор этой статьи все придумал?

Если немного изменить матрицу, то можно получить вращение по спирали или сделать из точки маятник.

💥 Видео

Радианная мера угла. 9 класс.Скачать

Поворот точки вокруг начала координатСкачать

Тригонометрическая окружность. Как выучить?Скачать

Алгебра 10 класс (Урок№29 - Радианная мера угла.)Скачать

Поворот точки вокруг начала координатСкачать

Физика - движение по окружностиСкачать

Как найти координаты точек на тригонометрической окружностиСкачать