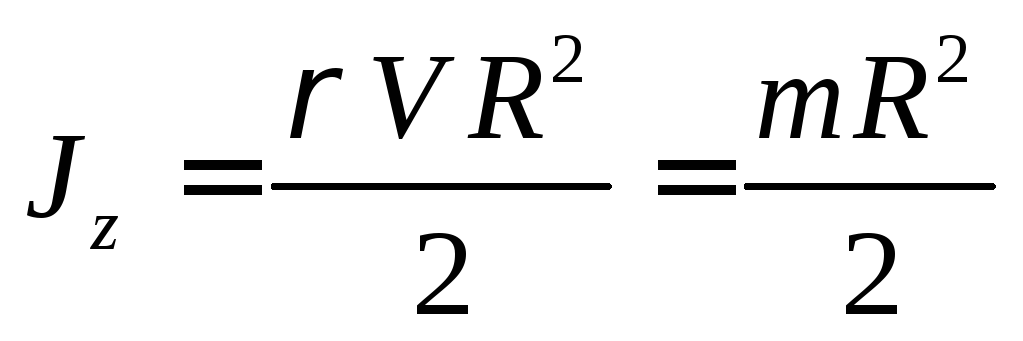Потенциальная энергия движения по окружности

Формула вычисления работы для поступательного прямолинейного движения имеет вид: W = F·s (Н·м) или (Дж).

Для того, чтобы вывести аналогичную формулу для вращательного движения, необходимо силу F преобразовать в момент силы M, а перемещение s, в угол Θ

Пусть для вращения колеса, радиусом r, прикладывается сила F, как показано на рисунке ниже.

Чему будет равна работа этой силы?

Для вычисления работы применим формулу:

При вращательном движении перемещение s будет равно произведению радиуса колеса r на его угол поворота Θ:

Момент М, создаваемой силой F, вычисляется по формуле:

Таким образом, работа будет равна:

Мы получили формулу вычисления работы для вращательного движения (угол поворота должен быть указан в радианах) — это произведение момента силы на угол поворота.

Вычислим работу, которую совершит колесо автомобиля после 10 оборотов, при условии, что к нему был приложен постоянный момент силы в 100 Н·м:

Видео:Физика - движение по окружностиСкачать

Кинетическая энергия вращательного движения

Кинетическая энергия объекта, массой m, движущегося поступательно со скоростью v, вычисляется по формуле: K = 1 /₂·(m·V 2 ).

Для получения формулы вычисления кинетической энергии для вращательного движения необходимо заменить массу тела m на момент инерции I, а скорость v на угловую скорость ω.

Формула связи тангенциальной скорости v и угловой скорости ω выглядит следующим образом (подробнее смотри «Параметры вращательного движения»):

Подставим это соотношение в предыдущую формулу:

Следует сказать, что данная формула расчета кинетической энергии подходит только для материальной точки.

Формула для вычисления кинетической энергии протяженного объекта будет выглядеть следующим образом:

В случае, если все материальные точки протяженного объекта вращаются с одинаковой угловой скоростью, ее можно вынести за знак суммирования:

Вспомним формулу момента инерции, и сделаем подстановку:

Закрепим полученные теоретические знания на практике, решив интересную задачу.

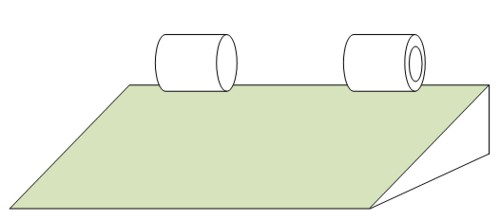
Предположим, что по наклонной плоскости скатываются два цилиндра одинаковой массы — полый и цельный. Выясним, какой из этих цилиндров скатится быстрее, т.е. будет иметь бОльшую скорость в конце наклонной плоскости.

Решая задачи подобного типа, надо понимать, что, если бы цилиндры просто скользили вниз по наклонной плоскости без вращения, то их потенциальная энергия превращалась бы в кинетическую энергию поступательного движения:

В нашем случае, потенциальная энергия цилиндров превращается в кинетическую энергию, как поступательного, так и вращательного движения:

Поскольку угловая скорость вычисляется по формуле ω=v/r, получим следующее равенство, и выведем формулу для вычисления скорости движения цилиндров:

Для обоих цилиндров все параметры в формуле одинаковы, за исключением момента инерции I (подробнее смотри «Момент инерции протяженного объекта»):

• для полого цилиндра: I=mr 2 ;
• для цельного цилиндра: I= 1 /₂mr 2

Подставляем соответствующие значения для момента инерции в формулу вычисления скорости цилиндров, и проводим несложные алгебраические преобразования:

Соотношение скоростей цилиндров будет равно:

Таким образом, скорость полого цилиндра будет немного ниже, чем цельного, следовательно, цельный цилиндр быстрее скатится по наклонной плоскости.

С физической точки зрения данный факт объясняется достаточно просто. В полом цилиндре основная масса материальных точек сосредоточена на краю цилиндра (на расстоянии радиуса от его центра), в то время, как в цельном цилиндре материальные точки распределены равномерно по всему радиусу, т.е., при одинаковой угловой скорости в полом цилиндре количество материальных точек, обладающих высокой тангенциальной скоростью, будет больше, чем в цельном, поэтому, полому цилиндру понадобится потратить больше энергии на свой разгон.

Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки:
Политика конфиденциальности Об авторе

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Потенциальная энергия движения по окружности

НЕОКЛАССИЧЕСКАЯ ФИЗИКА — КОРПУСКУЛЯРНАЯ КВАНТОВАЯ МЕХАНИКА

1. ОБ УНИВЕРСАЛЬНОЙ ЭНЕРГИИ ОТТАЛКИВАНИЯ

Раскрутим грузик на веревочке. При этом грузик имеет потенциальную энергию притяжения к центру вращения, но давайте усомнимся в том, что грузик, двигаясь по окружности, обладает кинетической энергией, а будем считать ее потенциальной отталкивания. Казалось бы, что этот вопрос чистой условности и не имеет принципиального значения, ведь услужливая математика способна соответствующим образом оформить и эту идею. Однако в дальнейшем увидим, что это не так, что эта идея совпадает с мнением Создателя на этот счет. Вопрос о потенциальной и кинетической энергии тела специально не исследовался, т.к. ортодоксальной наукой представляется очевидным испокон веку:

— Кинетическая энергия тела является мерой его механического движения и измеряется той работой, которую может совершить это тело при его торможении до полной остановки.

— Потенциальной энергией называется энергия, зависящая только от взаимного расположения взаимодействующих материальных точек или тел. (Б.М. Яворский, А.А. Детлаф, “Справочник по физике для инженеров и студентов вузов”, “Наука”, М., 1964, стр. 58,59).

Дж. Орир в книге: “Популярная физика” (стр. 132-134) дает следующие определения кинетической и потенциальной энергии тел.

Половина произведения массы тела на квадрат его скорости называется кинетической энергией этого тела. Вся произведенная над телом работа по изменению величины его скорости проявляется в виде кинетической энергии тела.

Тело приобретает потенциальную энергию всякий раз, когда на него воздействует сила F_c (называемая консервативной), зависящая только от его положения, но не зависящая от пути. Наиболее общее определение потенциальной энергии дается выражением: , где — угол между направлением F_c и перемещением s.

Тело, двигающееся по окружности, неподвижно относительно центра вращения, поэтому обладает только потенциальной энергией. Отпустив веревку, мы увидим удаляющийся от центра грузик, т.е. некое его другое состояние. Кроме того, отпуская грузик на разном расстоянии от центра вращения (при том же моменте количества движения), мы убедимся, что чем ближе к центру вращается грузик, тем сильнее отталкивается от него. Математическое оформление энергии движущегося по орбите гравитационного или иного заряда, как некоего вида потенциальной энергии отталкивания (численно равной mV 2 /2) не представляет затруднений.

В связи с многочисленными вопросами читателей об универсальной потенциальной энергии отталкивания, я приведу здесь дополнительные разъяснения. Официальные формулировки кинетической и потенциальной энергии недостаточно корректны. Если в системе взаимодействующих тел расстояние между ними не меняется, то система обладает потенциальной энергией. Если тело движется равномерно и прямолинейно, то оно обладает кинетической энергией. Во всех остальных случаях смешанное состояние при котором кинетическая энергия переходит в потенциальную или наоборот или они присутствуют одновременно и независимо (шарик катится без трения по горизонтальной поверхности). Как известно, сила является производной энергии по расстоянию. Например, равномерно движущееся тело обладает кинетической энергией . Поскольку в этом случае V = const , то , т.е. равнодействующая всех сил равна нулю. При движении тела по окружности универсальная потенциальная энергия отталкивания . Чтобы найти универсальную силу отталкивания (центробежную), прежде чем дифференцировать W_P по радиусу надо применить закон сохранения момента импульса тела . Если m не меняется, то в соответствии с этим законом Vr == const . Тогда . Теперь можно найти центробежную силу . Момент импульса движущегося по окружности тела можно изменить произвольно, поэтому окончательно будем иметь . Если связь тела с центром вращения прервется, то потенциальная энергия универсального отталкивания полностью превращается в кинетическую энергию тела (расстояние между телами, которые взаимодействовали, стало меняться, а удаляющееся от центра тело движется равномерно и прямолинейно).

Приходится вновь возвращаться к этой теме с дополнительными разъяснениями. У читателей никак не укладывается в голове отсутствие кинетической энергии у тела движущегося по окружности. Мы настолько привыкли считать, что движущееся тело может кого-нибудь стукнуть. А раз может стукнуть – значит обладает кинетической энергией. Для определенности, рассмотрим поведение спутника Земли. Оказывается, что в направлении перпендикулярном орбите спутник никого стукнуть не может, поэтому не обладает кинетической энергией в этом направлении. Если он стукнет кого-нибудь в направлении орбитального движения или по нему стукнет, например, метеорит в том же направлении, то часть потенциальной энергии универсального отталкивания превратится в кинетическую энергию в направлении перпендикулярном орбите и спутник займет в результате другую орбиту с новым значением потенциальной энергии универсального отталкивания и нулевой кинетической энергией до следующего возможного столкновения. Предположим, что в него попал метеорит со встречным движением. В этот момент нарушилось равновесие между силой притяжения к Земле и центробежной силой. Из этого равновесия легко получается выражение для первой космической скорости на устойчивой орбите: ( a ). В момент удара равенство ( a ) превратилось в неравенство: ( b ). Сила притяжения к Земле становится больше центробежной силы, поэтому, чтобы восстановить статус-кво приходится уменьшать радиус орбиты до нового баланса сил: , что эквивалентно увеличению потенциальной энергии универсального отталкивания ( r ₁ r ). Таким образом потенциальная энергия универсального отталкивания принимает нулевое значение только на бесконечности и увеличивается при приближении орбиты к центральному телу. С учетом закона сохранения момента количества движения потенциальная энергия универсального отталкивания обратно пропорциональна квадрату расстояния до центрального тела, а энергия гравитационного притяжения обратно пропорциональна расстоянию до центрального тела в первой степени. В результате сложения, ход изменения потенциальной энергии в зависимости от расстояния до центрального тела будет иметь потенциальную яму о существовании которой официальная астрономия не знает. В результате для нее остается загадкой, почему орбиты планет имеют наблюдаемое положение, а не какое-нибудь другое.

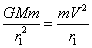
Еще одно доказательство отсутствия кинетической энергии у тела, движущегося по окружности, состоит в следующем. Представим себе, что в невесомости тело массой m мы привязали к неподвижной оси вращения на длинной нити, немного натянули нить и толкнули тело в направлении перпендикулярном нити с почти нулевой скоростью. Будем считать, что в начальный момент наша система имела нулевую кинетическую и потенциальную энергию из-за незначительной скорости начального вращения вокруг оси. Постепенно нить наматывается на ось вращения, ее длина уменьшается, а линейная скорость движения массы увеличивается. Что мы будем наблюдать при уменьшении радиуса вращения, например, в 2 раза? Очевидно, что линейная скорость вращающейся массы станет значительной и как угодно большой при достаточной начальной длине нити. Очевидно, что энергия нашей системы увеличилась до значительной величины. Теперь надо выяснить, откуда она появилась и что это за энергия. В противном случае легко создать вечный двигатель, который ловит пролетающие предметы, раскручивает их и отбрасывает с большой кинетической энергией. Вращающаяся масса находится под действием двух сил – силы натяжения нити и центробежной силы. Эти силы не уравновешены, т.к. сила натяжения нити все время немного больше центробежной силы за счет чего масса постепенно перемещается к центру вращения. Таким образом, работу совершает сама нить, преодолевая центробежную силу. Очевидно, что величина этой работы будет равна , где V – достигнутая линейная скорость массы. Полученную энергию никак нельзя связать с кинетической энергией массы т.к. в направлении перпендикулярном движению любая сила работу не совершает, а в направлении линейной скорости никакая сила не действует. Разрешение этого парадокса состоит в том, что при сближении с осью вращения увеличивается потенциальная энергия универсального отталкивания, а с какой скоростью происходит это сближение не имеет значения, что характерно именно для потенциальной энергии. Ситуация аналогична той, при которой подъемный кран поднимает груз, наматывая трос на барабан.

Таким образом, я ответил на вопросы А. Пуанкаре относительно потенциальной энергии, которые до сих пор оставались без ответа (Г.М. Голин, С.Р. Филонович. Классики физической науки. М., 1989, стр. 492): «Чтобы материализовать энергию, ее нужно локализовать; в отношении кинетической энергии это просто, но не так обстоит дело с энергией потенциальной. Где локализовать потенциальную энергию, вызванную притяжением двух небесных тел? В одном из двух? В обоих? В промежуточном пространстве?». В универсальной энергии отталкивания этих тел от центра масс вокруг которого они вращаются.

Еще один вопрос, на котором надо остановиться при рассмотрении движения тела по окружности — это вопрос существования центростремительного ускорения не как математической абстракции, а как физической реальности. Человек на экваторе находится под действием «центростремительного ускорения», которое складывается с ускорением свободного падения, поэтому должен весить больше, чем на полюсе. Однако в действительности все обстоит наоборот: центробежная сила частично компенсирует силу веса. Поэтому фиктивной является не центробежная сила (как утверждают ортодоксы) а «центростремительное ускорение».

Ускорением называется векторная величина w, характеризующая быстроту изменения скорости движущейся точки и равная первой производной от скорости по времени: . Вектор ускорения лежит в соприкасающейся плоскости, проходящей через главную нормаль и касательную к траектории, и направлен в сторону вогнутости траектории (Б.М. Яворский, А.А. Детлаф “Справочник по физике для инженеров и студентов вузов”, “Наука”, М., 1964, стр.20).

Понятие центростремительного ускорения вводится различным образом. Мы воспользуемся книгой: Дж. Б. Мэрион “Физика и физический мир”, “Мир”, М., 1975, стр. 126. Рассмотрим равномерное движение тела по окружности.

Поскольку векторы скорости V₁ и V₂ перпендикулярны к радиусам окружности r , то треугольник, образованный двумя радиусами и хордой x, подобен треугольнику, образованному V₁, V₂ и V. Оба треугольника равнобедренные, причем углы между равными сторонами у них одинаковы и равны Таким образом, численное значение изменения скорости:. Ускорение определяется выражением: .

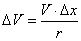
Подставляя значение V и вынося за знак предела постоянные величины, получим: . При уменьшении t до бесконечно малой величины хорда x становится равной дуге s , а предел отношения s / t равен линейной скорости V. Следовательно: . Нетрудно видеть, что вектор ускорения, совпадающий по направлению с вектором V , будет направлен к центру окружности, если рассматривать бесконечно малый промежуток времени.

Если считать, что движущееся по окружности тело обладает потенциальной энергией отталкивания, то на вопрос о существовании центростремительного ускорения мы сразу получаем однозначно отрицательный ответ. Когда официальная наука заявляет, что ускорение — векторная величина, имеющая направление, совпадающее с направлением изменения вектора скорости со временем, и приводит соответствующую формулу и схему определения разности векторов, она ставит телегу впереди лошади в том смысле, что заставляет физику адекватно отражать математику, а не наоборот. С физической точки зрения основной критерий равномерного движения тела по окружности предельно прост: линейная скорость его движения остается постоянной V=const. Попробуем перевести это высказывание на язык математики. Очевидно, что, в данном случае, приходится считать скорость не векторной, а скалярной величиной. В противном случае перевод станет нетождественным и приобретет противоположный физический смысл Vconst, т.к. одинаковыми считаются векторы с равным модулем и только параллельные друг другу. Поскольку математика не может дать больше того, что в нее изначально заложено, она и выдает нам ускорение, которого не существует. Это один из примеров того, что мы еще не научились правильно переводить на язык математики даже простые физические представления, это относится и к обратному переводу. Для неисправимых любителей жонглировать векторами, можно вообще отказаться от скорости со стрелочкой и заменить ее отношением длины орбиты к периоду вращения. Такое отношение при всем желании невозможно представить в виде вектора, т.к. числитель и знаменатель его скалярные величины.

Имеется простая экспериментальная возможность свести к нулю силу притяжения к центру вращения и в то же время оставить без изменения силу отталкивания от центра. Для этого надо находиться внутри капсулы, стенки которой жестко связаны с центром вращения. Внутри этой капсулы мы совершенно четко будем фиксировать изменение силы отталкивания в зависимости от радиуса вращения при одном и том же механическом моменте системы не только простыми физическими опытами, но и собственными ощущениями. Попробуем опустить шарик на пол этой вращающейся капсулы. Он покатится с ускорением, определяемым вторым законом Ньютона, под действием силы универсального отталкивания, но не к оси вращения, а в противоположную сторону, и остановится лишь тогда, когда сила универсального отталкивания, действующая на шарик, уравновесится противодействием стенки капсулы, которое также действует на шарик.

Еще один веский аргумент в пользу того, что ускорение при движении по окружности отсутствует, состоит в следующем. Закон сохранения энергии регламентирует излучение фотонов только при отрицательном ускорении электрического заряда (тормозное излучение), при положительном ускорении энергия поглощается из окружающей среды и излучение невозможно. “Ускорение”, связанное только с изменением направления вектора скорости не имеет ни положительного, ни отрицательного знака. На языке математики это обозначает нуль, а на языке физики — отсутствие ускорения. Синхротронное излучение, которое приводят, якобы, прямым доказательством излучения при равномерном движении электрического заряда по окружности, будет рассмотрено в теории атома (см. также главу 11.5), оно имеет совершенно другую природу.

В рассматриваемом случае центростремительная сила (лучше сказать — сила притяжения) перпендикулярна вектору скорости, следовательно, работу не совершает и ускорения не вызывает. На этом основании введение понятия центростремительного ускорения нанесло очевидный вред физике (особенно физике микромира), хотя и понятно, как стремление «сохранить» второй закон Ньютона. Ниже мы увидим, что в случае движения тела по окружности второй закон Ньютона справедлив, но по другим причинам.

Равномерное движение тела по окружности является полной аналогией равномерного движения шарика по горизонтальной поверхности. При этом сила притяжения шарика к Земле, приложенная к шарику, уравновешивается силой реакции опорной поверхности, также приложенной к шарику, поэтому шарик покоится в направлении действия этих сил (поскольку находится в потенциальной яме). При этом ему ничто не мешает равномерно двигаться в перпендикулярном направлении, не совершая работы. Точно то же происходит и при движении тела по окружности, где сила притяжения может быть любого происхождения, а сила отталкивания от центра вращения универсальна для любых тел. Эти две силы уравновешены, а движение в направлении, перпендикулярном действию сил, происходит без совершения работы.

Отрицая существование центростремительного ускорения, мы одновременно отрицаем и первый закон Ньютона для движения тела, ставя в совершенно равноправные условия равномерное движение тела по окружности и равномерное прямолинейное движение. Забегая вперед, можно сказать, что любые свободные тела, начиная от микрочастиц и кончая космическими объектами одновременно реализуют эти два права в равной мере, двигаясь по винтовой линии с равной поступательной и тангенциальной скоростью. Далее мы увидим, что для понимания движения микрочастиц и космических объектов приходится жертвовать не только первым, но и третьим законом Ньютона и эта жертва оказывается оправданной. После такого заявления автор уверен, что приверженцы догматов в науке покинут читательскую аудиторию, поэтому обращается к оставшимся с просьбой набраться терпения, которое будет вознаграждено.

Для большей ясности этого вопроса рассмотрим, на первый взгляд, бесспорный случай, в котором движущийся электрический заряд не излучает фотоны — равномерное и прямолинейное движение его (фигура 1.1).

Электрический заряд массой m равномерно движется по прямой АВ из бесконечности А в бесконечность В. Возьмем произвольную точку С с которой заряд никак не взаимодействует. Рассмотрим движение заряда относительно этой точки. В точке 1 кратчайшего расстояния от С до АВ момент количества движения заряда относительно С: . Для любой произвольной точки 2 на прямой АВ можно найти проекцию V₁ на касательную к окружности радиуса r₂, которую обозначим V₂. Из подобия двух треугольников находим, что .

Все рассуждения не изменятся, если тело m вращалось вокруг точки C , а в точке 1 связь оборвалась. Таким образом, при равномерном и прямолинейном движении тела его момент импульса относительно любой точки пространства остается тем же самым и объясняет инерцию тел. Инерция – это проявление закона сохранения момента импульса тела. Любые попытки изменить скорость тела или направление этой скорости связаны с затратой энергии на изменение момента импульса тела.

Этот результат можно интерпретировать, как вращение заряда массой m вокруг точки С в полном соответствии с законом сохранения момента количества движения S. При этом заряд «притягивается» к точке С, уменьшая радиус вращения и, соответственно, увеличивая скорость вращения, а затем «отталкивается» от нее, увеличивая радиус вращения и уменьшая скорость вращения. Правда, во всем этом процессе при движении заряда из А в В совершается всего пол-оборота вокруг точки С, но суть дела от этого не меняется. Электрический заряд не излучает энергию, не только двигаясь по стационарной круговой орбите, но и по орбите любой формы, при условии сохранения полной энергии, или если он находится в потенциальной яме (см. теорию атома). При этом он может участвовать и в других движениях, при том же условии. Кто не согласен с этим выводом, настаивает на том, что возможность излучения зависит от выбора системы отсчета, что явный абсурд. А как же быть с выводами электродинамики, спросите Вы, которые однозначно указывают на то, что движущийся по окружности заряд должен терять энергию через электромагнитное излучение? Здесь официальная физика использует для обмана читателя или по собственному неразумению следующий прием. Теорию излучения электрического диполя применяют к движению электрического заряда по окружности. Если один наблюдатель видит вдоль плоскости вращения колеблющийся электрический заряд и это движение можно было бы сравнить с диполем, то давайте посадим второго наблюдателя под углом 90 0 относительно первого наблюдателя. Один наблюдатель будет утверждать, что излучение должно распространяться к нему, а к партнеру излучения нет. Точно такой же вывод сделает и второй наблюдатель. Излучение одновременно есть, и его нет, что указывает на неправомочность сравнения движения электрического заряда по окружности с электрическим диполем. Сравнение орбитального движения электрона с колеблющимся диполем ошибочно еще и в том, что за один период колебания диполя положительное ускорение дважды за период сменяется отрицательным ускорением, а центростремительное (новая физика отрицает его существование) ускорение электрона постоянно. Тем не менее, официальная физика широко использует не адекватные сравнения. В условиях монополизма на истину некому указывать на ошибки. Далее мы увидим что то, что мы называем электромагнитной волной имеет совершенно другую физическую природу, а уравнения Максвелла появились по той простой причине, что у него под рукой просто не было больше ничего подходящего для объяснения самораспространения света в пространстве.

Отрицание существования центростремительного ускорения автоматически снимает вопрос о потере энергии электроном, движущимся вокруг ядра, поскольку он движется без ускорения. Квантовая механика признает существование момента импульса электрона в атоме, следовательно, должна признать факт движения S -электрона вокруг ядра и объяснить устойчивость атома. В этом отношении первый постулат Бора более корректен, хотя он и не объясняет причины отсутствия излучения.

Первый постулат Бора: электроны могут двигаться в атоме только по определенным орбитам, находясь на которых, они, несмотря на наличие у них ускорения (выделено мной — В.К.), не излучают. Эти орбиты соответствуют стационарным состояниям электронов в атоме и определяются условием: , где r_n — радиус n-й орбиты, m_e∙_n∙r_n — момент количества движения электрона на этой орбите, h — постоянная Планка, n — целое число (n>0). Б.М. Яворский и А.А. Детлаф “Справочник по физике для инженеров и студентов вузов”, “Наука”, М., 1964, стр.670-671.

Из дальнейшего будет видно, что mV 2 /2 является универсальной потенциальной энергией отталкивания любых взаимодействующих систем, начиная от галактик и кончая составными частями «элементарных» частиц. Отталкивание одноименных электрических зарядов и одноименных магнитных полюсов, как увидим, не имеет решающего значения в сравнении с mV 2 /2 особенно для систем, затронутых в этой работе.

Чтобы раскрыть эту универсальную потенциальную энергию отталкивания в явном виде в зависимости от радиуса орбиты движущегося гравитационного заряда (некоторой массы) или электрического заряда (тоже обладающего одновременно и гравитационным зарядом), что совершенно необходимо для применения математического аппарата, решим систему уравнений:

(1.1),

(1.2),

(1.3).

Формулой (1.3) мы воспользуемся за неимением ничего лучшего для связи массы тела со скоростью его движения (см. главу об “элементарных” частицах, где раскрыт физический смысл этой формулы и главу 5.2).

Решение системы уравнений:

(1.4).

При r больших (этот случай перекрывает диапазон размеров от радиуса атома до радиусов галактик и соответствует отсутствию заметного релятивистского увеличения массы, значительно превышает S 2 ), из (1.4):

(1.5).

При r малых (этот случай относится к «элементарным» частицам и их внутренним частям и соответствует значительному релятивистскому увеличению массы, когда , значительно меньше S 2 ), из (1.4):

(1.6).

Подставляя в (1.5) и в (1.6), нетрудно убедиться в том, что в первом случае получим , а во втором .

Экспериментальная (1901-1909 гг.) зависимость массы электрона от скорости его движения (точки). Кривая соответствует формуле (1.3) представлена на фигуре 1.2.

График заимствован из книги: Дж. Б. Мэрион “Физика и физический мир”, “Мир”, М., 1975, стр.30. Крестик на графике поставлен автором и смысл его будет раскрыт при описании электрона (см. также главу 5.2).

Столь же универсальной потенциальной энергии притяжения, казалось бы, не существует, например, притяжение космических объектов определяется гравитационными силами, электронов к ядру атома — электростатическими, а нуклонов в ядре – ядерными. Все-таки, забегая вперед, можно сказать, что все параметры космических систем, атомов и «элементарных» частиц, в конечном итоге, определяются универсальной потенциальной энергией притяжения, вид функции которой зависит от конкретных обстоятельств, и которую условно назовем гравидинамическим притяжением. Для его проявления нужны вращающиеся вокруг своей оси и перемещающиеся в пространстве гравитационные заряды. Поскольку все в Природе так или иначе вращается, а равномерное прямолинейное движение лишь абстракция, которой нет соответствия в реальном мире (что со всей очевидностью будет показано ниже), то проявления гравидинамического взаимодействия легко наблюдать как в космических масштабах, так и в микромире, а начиная от ядер атомов и кончая составными частями «элементарных» частиц, гравидинамическое притяжение проявляется практически в чистом виде. Здесь следует сразу оговориться, что в книге нет декларативных заявлений. Рано или поздно будет показана справедливость каждого высказывания. Например, будет показано, что все свободные тела движутся по винтовой линии, а первый закон Ньютона справедлив к оси этой линии, но не к самому телу.

Комментарии автора к главе 1:

1. Еще одно доказательство существования потенциального поля отталкивания при движении по окружности.

Здесь приведу математические доводы в пользу универсальной потенциальной энергии отталкивания при движении тела по окружности.

Как бы мы не подтягивали тело к центру окружности (резко или постепенно) или не отпускали, чтобы удалялось от центра, общая энергия будет равна нулю, если мы вернемся в исходную точку на то же расстояние от центра, (в любую точку окружности на этом расстоянии мы попадем без затраты энергии). Предположим, в исходном положении телу m на окружности с окружной скоростью V₀ и имеющему «кинетическую» энергию E мы сообщили дополнительную энергию W, тогда, очевидно, что: (1), где V – новая (текущая) окружная скорость. Из (1):(2). Запишем момент импульса тела на окружности: (3), где R — радиус вращения. Возведем (3) в квадрат и запишем квадрат скорости: (4). Подставим (4) в (2): (5). Подставим в (5) выражение момента импульса и преобразуем: (6). Выражение (6) показывает, что энергия, которую можно получить (или затратить) при изменении радиуса вращения обратно пропорциональна квадрату расстояния от центра вращения и в этом смысле потенциальное поле универсального отталкивания ничем не отличается от электростатического или гравитационного потенциального поля, только потенциальное поле отталкивания более круто изменяется с расстоянием от центра (не E

1/R 2 ). Это и определяет существование потенциальной ямы при электростатическом и гравитационном взаимодействии. Без потенциальной энергии отталкивания существование потенциальной ямы взаимодействия невозможно.

О кинетической энергии тела, двигающегося по окружности, можно рассуждать только для тела, жестко связанного с центром вращения. В этом случае любое изменение кинетической энергии тела не приводит к изменению радиуса вращения, т.е. закон сохранения момента импульса в этом случае не работает, а потенциальная энергия отталкивания не меняется.

1.1. При движении тел по окружности ускорения отсутствуют

На фигуре 1.1.1 показан диск 1 радиуса R . С диском жестко связан стержень 2 по которому свободно может скользить некоторая масса m . Начнем крутить диск с постоянной угловой скоростью . Очевидно, что положение m в центре диска неустойчиво и эта масса начнет скользить по стержню 2 к периферии диска под действием центробежной силы (не центростемительной, которой тут вообще нет). Поскольку, в данном случае, одновременно меняется и радиус вращения массы m и ее линейная окружная скорость:

V = × r (1.1.1),

то, очевидно, что формулу центробежной силы в виде:

(1.1.2)

применять нельзя. Подставим (1.1.1) в (1.1.2):

(1.1.3).

Из второго закона Ньютона очевидно, что центробежное ускорение для рассматриваемой массы будет:

(1.1.4),

которое с учетом (1.1.1) формально совпадает с выражением для «центростремительного» ускорения официальной физики:

(1.1.5).

Поскольку центробежная сила в соответствии с (1.1.3) линейно возрастает с радиусом, то ее среднее действующее значение будет равно половине максимального. Тогда работа совершенная этой силой на пути r :

(1.1.6).

Кинетическая энергия материальной точки массы m определяется таким же выражением:

, (1.1.7).

где — момент инерции массы m

Если на конце стержня поставить опору, то центробежная сила будет уравновешена реакцией этой опоры и в направлении действия этих сил перемещение и какое-либо ускорение отсутствуют. В этом случае рассматриваемая масса обладает кинетической энергией в соответствии с формулой (1.1.7). Приведенный анализ показывает, что спекуляции официальной физики вокруг «центростремительного» ускорения ошибочны. В рассматриваемой задаче существует только центробежное ускорение и то только до тех пор, пока мы позволяем массе свободно двигаться вдоль радиуса. При движении тела по окружности с фиксированным радиусом никаких ускорений нет.

Хочу напомнить приверженцам векторного мировоззрения, что квадрат вектора является скаляром не имеющим направления. В формуле (1.1.5) векторов вообще нет, даже если окружную скорость считать вектором. На этом основании излучение электрического заряда движущегося по окружности невозможно т.к. он не обладает ускорением какого-либо направления. Поэтому ученые сделали в свое время большую ошибку отвергнув теорию атома Бора.

В главе 1 показано, что при равномерном прямолинейном движении момент импульса тела относительно любой точки пространства остается одинаковым. Прямым следствием этого вывода является определение инерции тела, как проявления фундаментального закона сохранения момента импульса тела. Пока момент импульса тела не меняется, инерцию мы не наблюдаем. Как только начинаем ускорять или замедлять движение или изменять его направление, так сразу обнаруживается инерция. Любое изменение момента импульса связано с действием силы а она, в свою очередь, определяется скоростью изменения импульса тела в соответствии со вторым законом Ньютона:

(1.2.1)

Если силу F разложить по трем осям координат, то (1.2.1) можно переписать в скалярной форме скорости изменения компонентов импульса по этим осям. Этот факт указывает на независимость движений под действием любой составляющей суммарной силы. Таким образом, в соответствии со вторым законом Ньютона, чем медленнее изменяется момент импульса тела, тем меньшую силу нужно приложить к этому телу.

Варианты изменения момента импульса для прямолинейного движения тела показаны на фигурах 1.2.1 и 1.2.2.

На фигуре 1.2.1 в результате действия на тело некоторой силы на участке AB , имеющего момент импульса mV ₁ h относительно произвольной точки C , его момент импульса изменился и стал равным mV ₂ h . На фигуре 1.2.2 в результате действия на тело некоторой силы на участке AB имеющего момент импульса mV ₁ h ₁ относительно произвольной точки C , его момент ипульса изменился и стал равным mV ₁ h ₂.

Здесь необходимо вспомнить третий закон Ньютона: действие равно противодействию, а сила противодействия направлена противоположно действующей силе. Если формально применять этот закон, то можно прийти к принципиально ошибочным выводам. Например, мы действуем на тело с целью изменить его скорость или направление движения, но, встречая равное и противоположно направленное противодействие, мы не сможем изменить параметры движения этого тела. Картина взаимодействия тел становится ясной в опыте, когда гирю кладут на подушку. В этом эксперименте гиря, несмотря на соприкосновение с поверхностью подушки, вначале движется ускоренно под действием силы притяжения к Земле. В этот момент сила противодействия подушки плавно нарастает от нуля до некоторого значения, равного разнице веса гири и силы инерции ее, т.к. сила инерции гири направлена противоположно весу. В некоторый момент времени гиря движется уже равномерно и ее сила инерции пропадает. Сила сопротивления подушки продолжает увеличиваться и гиря движется уже замедленно, сила инерции возникает вновь и теперь она направлена по направлению действующей силы веса. Поэтому гиря прогибает поверхность подушки больше, чем в случае бесконечно медленного опускания гири. Наступает момент, когда гиря движется обратно. После нескольких колебаний или апериодического затухания их, устанавливается равновесие, при котором вес тела приложенный к гире уравновешен противодействием подушки, также приложенным к гире. Поэтому гиря находится в состоянии покоя. Для краткости, мы здесь не рассматриваем взаимодействие подушки с кроватью, кровати с полом, пола с Землей, Земли с Солнцем и т.д. Очевидно, поскольку все тела состоят из атомов, то идеально жестких тел в природе не существует и взаимодействие их непосредственным контактом аналогично рассмотренному взаимодействию гири с подушкой. Из описанного эксперимента можно сделать такой вывод: третий закон Ньютона справедлив только для равновесного состояния системы, которое может быть как статическим, так и динамическим (круговое вращение). Во взаимодействии тел участвуют три взаимосвязанных силы: сила действия, сила инерции и сила противодействия. Действующая сила независима от времени, а сила инерции и сила противодействия зависят от времени взаимодействия, причем сила инерции мгновенно реагирует на изменение момента импульса тела.

Рассмотрим теперь случай взаимодействия при круговом движении тела. В этой книге приведены многочисленные доказательства того, что все тела в Природе двигаются по винтовой линии. В тангенциальном направлении этого движения сила инерции присутствует постоянно в виде центробежной силы и обусловлена равенством этой силы и силы гравидинамического притяжения к оси винтовой траектории тела. Поэтому рассуждения, касающиеся фигуры 1.2.1 и 1.2.2 полностью справедливы к оси винтовой траектории тел (к поступательному перемещению тела). На фигуре 1.2.3 показано взаимодействие тела 1 с центральным телом 2 (это может быть человек, наматывающий на шпулю нить, связывающую его с телом 1 или ядро атома на которое «падает» электрон).

Равновесное состояние здесь достигается не сразу, аналогично падению гири на подушку и поэтому позволяет подробно рассмотреть взаимодействие.

В не релятивистской области масса тела 1 не меняется (m₀), момент импульса его зависит только от произведения

Vr==const (1.2.2),

поэтому момент импульса:

m ₀ Vr =m₀ (1.2.3).

Умножим обе части (1.2.3) на V/2r, тогда с учетом (1.2.2) получим:

E_k=m₀ 2 /2r 2 (1.2.4),

где E_k — кинетическая энергия тела. На самом деле (1.2.4) не кинетическая энергия вращающегося тела, а потенциальная энергия универсального отталкивания, численно равная mV 2 /2 (глава 1).

Дифференцируя (1.2.4) по радиусу с последующей подстановкой (1.2.2), найдем:

где F_цб — центробежная сила (сила инерции или сила универсального отталкивания в данном случае).

В релятивистской области скорость движения равна скорости света C, поэтому момент импульса зависит только от произведения

mr==const (1.2.6),

где m – релятивистская масса тела, поэтому момент импульса:

mCr =C (1.2.7).

Умножая обе части (1.2.7) на C/2r с учетом (1.2.6) и повторив манипуляции, аналогичные вышеприведенным для не релятивистского случая, получим релятивистскую силу универсального отталкивания:

В рассматриваемом взаимодействии тел действующая сила со стороны тела 2 на тело 1 может быть любого происхождения и изменяться по любому закону в зависимости от расстояния между телами. При этом действующая на тело 1 сила больше возникающей противодействующей силы которой, в данном случае, является центробежная сила инерции до тех пор, пока они не станут равными за счет увеличения силы инерции тела 1. При этом тело 1 будет двигаться по стационарной круговой траектории, обозначенной на фигуре 1.2.3 пунктиром. В этом состоянии на тело 1 действует сила притяжения со стороны тела 2 и на это же тело действует равная ей сила универсального отталкивания. Поэтому тело 1 покоится в направлении действия этих сил, но движется в перпендикулярном направлении без совершения работы аналогично катящемуся шару по горизонтальной плоскости. В рассматриваемом случае сила противодействия совпадает с силой инерции и равна действующей силе только в равновесном состоянии.

Видео:Потенциальная и кинетическая энергияСкачать

Закон сохранения энергии для вращательного движения

1. Момент импульса, законы изменения и сохранения момента импульса.

2. Работа и кинетическая энергия при вращательном движении. Закон изменения и сохранения механической энергии при вращательном движении.

3. Сопоставление поступательного и вращательного движений. Заключение.

ОТВОДИМОЕ ВРЕМЯ: 2 часа.

1. Суханов курс физики. – М.: 1996.

2. Савельев общей физики. Том 1. – M: – Наука, 1996. § 29, 41,42,43.

3. Трофимова физики. – М.: Высшая школа, 1999. § 17,19.

4. , Детлаф по физике. – М.: Наука, 1996. Глава 5.

Материальное обеспечение занятия:

Демонстрации: «Скамья Жуковского», «Фигурист».

Наряду с законами сохранения энергии и импульса закон сохранения момента импульса является одним из важнейших Фундаментальных законов природы.

В физике понятие, момента импульса расширяют на немеханические системы (которые не подчиняются законам Ньютона) и постулируют закон сохранения импульса для всех физических процессов.

I. МОМЕНТ ИМПУЛЬСА. ЗАКОН ИЗМЕНЕНИЯ И ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Вспомним основной закон динамики вращательного движения:

(1)

учтем, что и подставим в (1)

,

Поскольку предполагалось, что момент инерции J=const можно внести его под знак дифференциала.

Тогда получим . Векторную величину называют моментом импульса твердого тела относительно оси. Тогда можно записать так:

(2)

Скорость изменения момента импульса тела равна векторной сумме моментов сил, действующих на тело.

Это более общая формулировка основного закона вращательного движения, она справедлива и для тела с изменяющимся моментом инерции.

Момент импульса измеряется в 1кг·м/с. Килограмм-метр в квадрате в секунду равен моменту импульса тела с моментом инерции 1кг·м, вращающегося с угловой скоростью 1рад/с.

Момент импульса – вектор, его направление всегда совпадает с направлением угловой скорости (рис 1).

Выберем произвольную систему тел.

Ведем понятие момента импульса данной системы как векторную сумму моментов импульсов ее отдельных частей:

(3)

где все векторы определены относительно одной и той же оси враще­ния заданной системы отсчета. Момент импульса системы тел – величина аддитивная; момент импульса системы тел равен векторной сумме моментов импульсов ее отдельных частей независимо от того, взаимодействуют они между собой или нет.

Выясним, какая величина определяет изменение момента импульса системы тел. Продифференцируем (3) по-времени:

(4)

Из Формулы (2) ясно, что равна моменту всех сил, действующих на i-ю часть системы тел. Представим момент в виде векторной суммы моментов внутренних и внешних сил:

(5)

где – суммарный момент всех внутренних сил относительно данной оси, – суммарный момент всех внешних сил относительно той же оси.

Суммарный момент всех внутренних сил относительно любой точки равен нулю, так как внутренние силы – это взаимодействия между частицами системы. По третьему закону Ньютона эти силы попарно равны по модулю, противоположны по направлению и лежат на одной прямой, то есть имеют одинаковые радиус-векторы. Поэтому моменты сил каждой пары взаимодействия равны по модулю и противоположны по направлению, Значит, суммарный момент всех внутренних сил равен нулю.

(6)

В результате уравнение (5) принимает вид:

(7)

где – суммарный момент всех внешних сил, называемый также главным моментом.

Производная момента импульса системы по времени равна суммарному моменту всех внешних сил относительна данной оси.

Пришли к важному выводу в уравнении (7): момент импульса системы тел может изменяться под действием только суммарного момента всех внешних сил.

В проекциях на оси неподвижной прямоугольной декартовой сис­теме координат с началом в точке 0 закон изменения момента импуль­са системы записывается в виде:

(8)

Здесь Lx, Ly, Lx и Mx, My, Mx – моменты импульса системы и главные моменты внешних сил относительно соответствующих осей координат.

Из основного закона динамики вращательного движения следует закон сохранения момента импульса.

Момент импульса замкнутой системы относительно любой неподвижной точки не изменяется с течением времени.

Для замкнутой системы ; ,

(9)

Закон сохранения момента импульса принадлежит к числу самых фундаментальных физических законов, он связан с изотропностью пространства. Изотропность пространства проявляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора направления осей координат инерциальной системы отсчета, т. е. не изменяются при повороте в пространстве замкнутой системы как целого на любой угол.

Особый интерес представляет случай, когда момент импульса сохраняется для незамкнутой системы. Если относительно некоторой оси выбранной системы отсчета главный момент внешних сил то момент импульса системы тел относительно этой оси сохраняется.

Обычно и Однако, если главный момент внешних сил относительно какой-либо оси, проходящей через точку 0, тождественно равен нулю, то момент импульса системы относительно этой оси не изменяется с течением времени. Например, если , то Такой случаи рассматривается в демонстрации со скамьей Жуковского (рис. 2).

Система тел: скамья, человек, гантели,

Эта система не замкнутая, но момент внешних сил относительно вертикальной оси Z равен нул^, следовательно

(10)

Подставляем

Найдем (11)

где J0 – момент инерции скамьи с человеком, m – масса одной гантели, r1 – расстояние гантели до оси в первом случае, r2 – расстояние гантели до оси во втором случае.

возрастает, если r2

Пусть твердое тело движется поступательно под действием консервативных и неконсервативных сил, т.е. общий случай. Тогда равнодействующая всех сил, действующих на тело 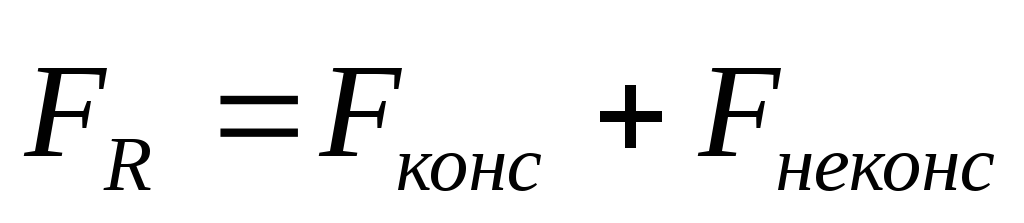. Работа равнодействующей всех сил в этом случае.

По теореме о кинетической энергии , а также учитывая, что, получим

– полная механическая энергия тела

(_*)

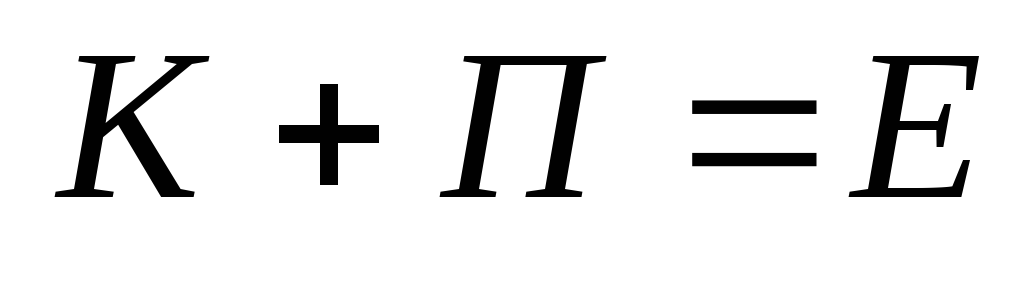
Если , то. Это и есть математическая запись закона сохранения энергии в механике для отдельного тела.

Формулировка закона сохранения энергии:

Полная механическая энергия тела не изменяется в отсутствии работы неконсервативных сил.

Для механической системы из Nчастиц нетрудно показать, что (_*) имеет место.

, при этом

Первая сумма здесь – суммарная кинетическая энергия системы частиц.

Вторая – суммарная потенциальная энергия частиц во внешнем поле консервативных сил

Третья – потенциальная энергия взаимодействия частиц системы друг с другом.

Вторая и третья суммы представляют собой полную потенциальную энергию системы.

, т.е.

Работа неконсервативных сил состоит из двух слагаемых, представляемых собой работу внутренних и внешних неконсервативных сил .

Также как и в случае движения отдельного тела, для механической системы из Nтел, если, то, и закон сохранения энергии в общем случае для механической системы гласит:

Полная механическая энергия системы частиц, находящихся только под действием консервативных сил, сохраняется.

Таким образом, при наличии неконсервативных сил полная механическая энергия не сохраняется.

Неконсервативными силами являются, например, сила трения , сила сопротивленияи другие силы, действия которых вызывают дессинацию энергии (переход механической энергии в теплоту).

Силы, приводящие к дессинации называются дессинативными. Некоторые силы не обязательно являются дессинативными.

Закон сохранения энергии имеет всеобщий характер и применим не только к механическим явлениям, но и ко всем процессам в природе. Полное количество энергии в изолированной системе тел и полей всегда остается постоянным. Энергия лишь может переходить из одной формы в другую.

Динамика вращательного движения

Видео:Движение тел по окружностиСкачать

§12. Кинетическая энергия вращательного движения твердого тела. Момент инерции тел

Рассмотрим твердое тело, вращающееся на неподвижной оси.

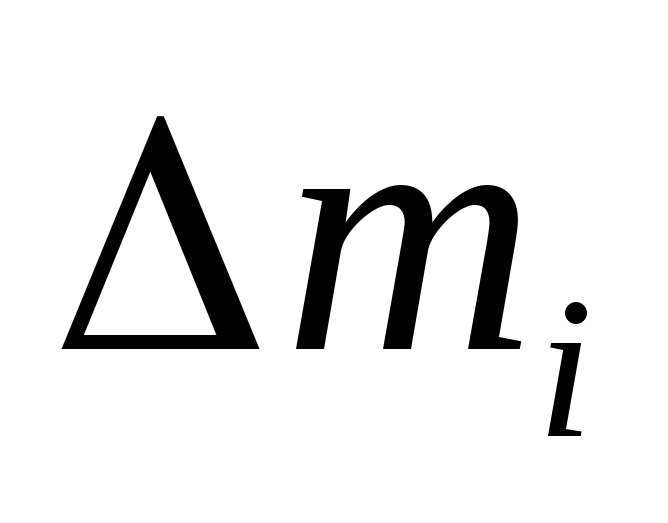
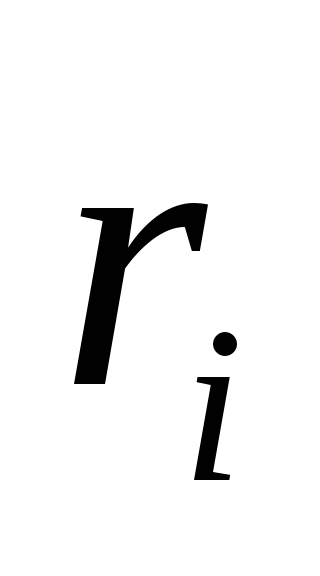
Мысленно разобьем его на Nэлементарных участков с массой, расстояние от которых до оси вращениямного больше линейных размеров участка. Тогда кинетическая энергия вращения тела вокруг осиzбудет равна сумме кинетических энергий всех элементарных участков,

(т.к. кинетическая энергия – величина аддитивная).

Ясно, что все элементарные участки вращаются по окружности, разного радиуса, но с одинаковой угловой скоростью ; для любого участка можно записать. С учетом этого равенства

Если размеры тела много меньше расстояния от него до некоторой его оси вращения z, то произведение массы этого тела на квадрат расстояния до данной оси вращения называется моментом инерции этого тела относительно оси вращенияz:

В нашем случае – моменты инерцииi-ых участков относительно осиz.

Моментом инерции всего тела вращения называется сумма моментов инерции всех его элементарных частей

Суммирование по элементарным участкам определяется разбиением, и лишь при , аесть предел и от разбиения не зависит. Поэтому точная формула для момента инерции есть:

Таким образом, кинетическая энергия есть

поступательное движение вращательное движение

– быстрота или скорость– скорость вращения

– мера инертностимера инертности

при движении при вращении

Моменты инерции некоторых однородных (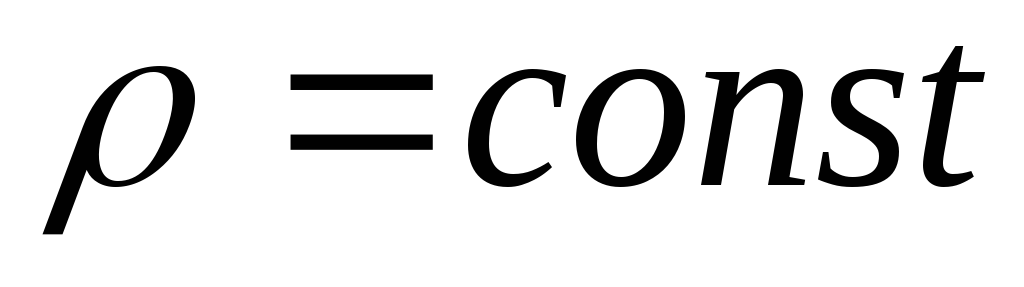) тел.

Момент инерции обруча или тонкостенного цилиндра относительно оси, проходящей через центр инертности перпендикулярно плоскости обруча.

Момент инерции диска или цилиндра относительно оси симметрии тела.

Выберем внутри цилиндра тонкостенный цилиндр с и толщиной.

Учитывая, что , получим

.

Момент инерции плоского стержня относительно оси, проходящей через центр тела и перпендикулярно к нему

Момент инерции шара относительно оси, проходящей через его центр.

1. Момент импульса вpащающегося, тела относительно оси

L = Jw.

2. Закон сохpанения момента импульса

SL = const.

где L – момент импульса i-го тела, входящего в состав системы. Закон сохpанения момента импульса для двух взаимодействующих тел

где J₁, J₂, w₁, w₂ – моменты инеpции и угловые скоpости

тел до взаимодействия, J₁ / , J₂ / , w₁ / , w₂ / – те же величины после

взаимодействия. Закон сохpанения момента импульса для одного тела, момент инеpции, котоpого меняется,

где J₁ и J₂ – начальный и конечный моменты инеpции, w₁ и w₂ –

начальная и конечная угловые скоpости тела.

3. Между формулами, описывающими поступательное и вращательное движения есть аналогия:

W_k = ( mv 2 )/2; W_k = (Jw 2 )/2;

С. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ.

1. Уравнение гармонических колебаний

x = Acos(wt + j),

где х– смещение точки от положения равновесия;t – время;

А, w, j – соответственно амплитуда, угловая частота, начальная фаза колебаний; (wt + j)-фаза колебания в моментt

2. Угловая частота колебаний w = 2pn, или w = 2p/T,

где n и T – частота и период колебаний.

3. Скорость точки, совершающей гармонические колебания,

v = x / = – Awsin(wt + j).

4. Ускорение при гармоническом колебании

a = x // = – Aw 2 cos(wt + j).

5. Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящими по одной прямой, определяется по формуле

где А₁ и А₂ – амплитуды составляющих колебаний; j₁ и j₂ – их начальные фазы.

6. Дифференциальное уравнение гармонических колебаний материальной точки mx // = – kx, или x // + wx = 0,

гдеm – масса точки; k -коэффициент квазиупругой силы (kw 2 ) . 7. Полная энергия материальной точки, совершающей гармонические колебания, W = (mA 2 w 2 )/2 = (kA 2 )/2.

8. Период колебаний тела, подвешенного на пружине

T = 2pÖ(m/k),

где m – масса тела; k– жесткость пружины.

9. Период колебаний математического маятника T = 2pÖ(l/g),

гдеl – длина маятника; g – ускорение свободного падения.

10. Период колебаний физического маятника T = 2pÖ(J/mgl).

11. Период крутильных колебаний тела, подвешенного на упругой нити T = 2pÖ(J/k),

где J– момент инерции тела относительно оси, совпадающей с упругой нитью; k – жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается.

12. Дифференциальное уравнение затухающих колебаний

mx // = – kx – rx / , или x // +2dx / + w 2 x = 0,

где r – коэффициент сопротивления; d – коэффициент затухания; d = r/(2m); w – cобственная частота колебаний (w = Ö(k/m).

13. Уравнение затухающих колебаний x = A . e – d t .cos(wt + j)

где А – начальная аплитуда; w – частота; е – основание натурального логарифма; d – коэффициент затухания.

14. Дифференциальное уравнение вынужденных колебаний

mx // = – kx – rx / + F .cos(wt), или x // + 2dx / + w 2 x = f .cos(wt).

где F .cos(wt) – внешняя периодическая сила, действующая на колеблющуюся точку и вызывающая вынужденные колебания; F – ее амплитудное значение; f = F /m.

Вариант 1.

Кинематика.

А.1. Пуля пущена с начальной скоростью vпод углом aк горизонту. Определить максимальную высоту подъема, дальность полета и радиус кривизны траектории пули в ее наивысшей точке.

Динамика.

Б.1.Через блок массой Мперекинута невесомая, нерастяжимая нить, к концам которой подвешены грузы с массами m₁и m₂ . Определить ускорения, с которыми будут двигаться грузы, если их предоставить самим себе, трением в оси блока пренебречь.

Законы сохранения при прямолинейном движении.

В.1.Тело массой m₁движется навстречу второму телу массой m₂ и абсолютно не упруго соударяется с ним. Скорости тел непосредственно перед ударом были v₁ и v₂ . Определить расстояние, пройденное телами после удара, если коэффициент трения μ ?

Энергия и работа.

Д.1. Под действием постоянной силы F вагонетка прошла путь Sи приобрела скорость v . Определить работу силы, если масса вагонетки равна m и коэффициент трения k .

Законы сохранения при вращательном движении.

Е.1. Стержень длиной Lи массой M может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня. В середину стержня ударяет пуля массой m₂,летящая в горизонтальном направлении со скоростью vи застревает в нем. На какой угол отклонится стержень после удара?

6. Механические колебания.

С.1.Частица массой m совершает гармонические колебания с циклической частотой ω , по закону x= Asin(ωt). Определить период колебаний и амплитуду колебаний, если максимальная сила, действующая на частицу, равна F . Определить, также кинетическую, потенциальную и полную энергии через время tот начала колебания.

Вариант 2.

Кинематика.

А.2. Точка движется по окружности так, что зависимость пути от времени дается уравнением S = А – Bt + Ct 2 . Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорения.

Динамика.

Б.2.Акробат на мотоцикле описывает «мертвую петлю» радиусом R. С какой наименьшей скоростью должен проезжать акробат верхнюю точку петли, чтобы не сорваться?

🌟 Видео

Потенциальная энергияСкачать

Кинетическая и потенциальная энергияСкачать

Урок 125. Работа, мощность и кинетическая энергия при вращательном движенииСкачать

Движение по окружности 2Скачать

Урок 118. Потенциальная энергия гравитационного взаимодействия. Вторая космическая скоростьСкачать

Урок 86 (осн). Энергия. Превращения энергииСкачать

Урок 116. Работа силы тяжести. Потенциальная энергия тела, поднятого над ЗемлейСкачать

Энергия. Кинетическая и потенциальная энергия | Физика 7 класс #48 | ИнфоурокСкачать

Потенциальная и Кинетическая🤔Скачать

Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Энергия. Кинетическая и потенциальная энергия. 7 класс.Скачать

Вращательное движение. 10 класс.Скачать

Физика 10 класс (Урок№13 - Работа. Мощность. Энергия. Закон сохранения механической энергии.)Скачать

Многоуровневая задача. Закон сохранения энергии и движение по окружности.Вес телаСкачать

КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Кинематика Урок №8. Движение по окружности. Физика ЕГЭ 2022Скачать