Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Построение углов заданной градусной мерыСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
ТЕХНОЛОГИЧЕСКАЯ КАРТА УЧЕБНОГО ЗАНЯТИЯ
Изучить радианный метод измерения углов вращения и их связь с
градусной мерой. Изображать углы вращения на окружности, соотносить
величину угла с его расположением.
Формировать умения сравнивать и обобщать, выделять главное, развивать умение логически мыслить, делать выводы.
обучать объективной оценке своих возможностей и успехов;
способствовать развитию навыков устной речи, умению грамотно вести диалог и аргументировать свои действия;
осознание большой практической значимости производной в жизни человека.
1.Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
2.Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
3.Анализировать рабочую ситуацию, осуществлять текущий и итоговый контроль, оценку и коррекцию собственной деятельности, нести ответственность за результаты своей работы.
4.Работать в коллективе и команде, эффективно общаться
– владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием
-Сформированность представлений о математике как универсальном языке науки
— понимание значимости математики для научно-технического прогресса, сформированность отношения к математике, как к части общечеловеческой культуры через знакомство с историей развития математики
— развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышленияна уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;
— готовность и способность к самостоятельной, творческой и ответственной деятельности
Умение самостоятельно определять цели деятельности и составлять планы деятельности;
Самостоятельно осуществлять, контролировать и корректировать деятельность;
— использовать всевозможные ресурсы для достижения поставленных целей и реализации планов деятельности;
— выбирать успешные стратегии в различных ситуациях;
-умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты.
Организация образовательной среды
технология кооперативного обучения;
технология развивающего обучения;
Раздаточные материалы, учебники, мультимедийная доска
Парная, индивидуальная, групповая
Приветствует обучающихся. Отмечает
отсутствующих. Настраивает обучающихся на продуктивную деятельность
Настраиваются на продуктивную мыслительную деятельность
Корректирует и конкретизирует тему и цель занятия, организует деловое общение, способствующее актуализации опорных знаний и целеполагания
Пытаются определить и сформулировать тему и цель занятия по предложенной информации, размещенной на слайде электронной презентации
Этап открытия новых знаний
Организует деловое общение, способствующее актуализации опорных знаний
Записывают опорный конспект:
Радиан — это центральный угол, у которого длина дуги и радиус имеют равные величины ( AmB = AO ).
Значит, радианная мера измерения угла — это отношение длины дуги, которая проведена произвольным радиусом и заключёна между сторонами этого угла, к радиусу дуги.
Из этой формулы, длину окружности C и радиус r этой окружности выражаем так:
Таким образом, полный оборот, который равен 360° в градусном измерении , равен двум в радианном измерении. Отсюда выводим значение 1-го радиана:
Таблица значений самых распространенных углов в градусах и радианах:
По этой таблице очень удобно производить перевод градусов в радианы и радианы в градусы.
Этап закрепления новых знан
Контролирует работу обучающихся, фиксирует результаты
Индивидуально выполняют практическую работу
Этап подведения итогов занятия
Подводит итоги, анализирует содержание и ошибки
Оценивает работу обучающихся, организует диалоговое общение, стимулирующее рефлексивную деятельность, оценку и взаимооценку. Подводит итоги проделанной работы. Выставляет отметки обучающимся
Оценивают свою работу на занятии, осуществляют взаимооценку
Инструктирует по выполнению
Записывают домашнее задание
Практическая работа «Радианная и градусная мера угла»
1. Постройте угол в 450 0 2. Постройте угол –550 0
3. Закончите определение: Радианом называется угловая мера дуги окружности, длина которой _____________________________________
4. Выразите данные углы через радианную меру:
5. Выразите данные углы через градусную меру:
«РАДИАННАЯ И ГРАДУСНАЯ МЕРЫ УГЛА»
ПЕРЕВЕДИТЕ ИЗ РАДИАННОЙ МЕРЫ В ГРАДУСНУЮ: 












ПЕРЕВЕДИТЕ ИЗ ГРАДУСНОЙ МЕРЫ В РАДИАННУЮ: 30 0 ; 150 0 ; 300 0 ; 2100 0 ;
350 0 ; 360 0 ; 700 0 ; 35 0 ; 60 0 ; 760 0 ; 45 0 ; 60 0 ; 130 0 ; 90 0 ; 270 0 ; 180 0 ; 0 0 ; 720 0 ; 55 0 .
Практическая работа «Радианная и градусная мера угла»
1. Постройте угол в 590 0 2. Постройте угол –470 0
3. Закончите определение: Радианом называется угловая мера дуги окружности, длина которой _____________________________________
4. Выразите данные углы через радианную меру:
5. Выразите данные углы через градусную меру:
«РАДИАННАЯ И ГРАДУСНАЯ МЕРЫ УГЛА»
1) ПЕРЕВЕДИТЕ ИЗ РАДИАННОЙ МЕРЫ В ГРАДУСНУЮ: 












2) ПЕРЕВЕДИТЕ ИЗ ГРАДУСНОЙ МЕРЫ В РАДИАННУЮ: 430 0 ; 450 0 ; 900 0 ;
390 0 ; 33 0 ; 15 0 ; 10 0 ; 20 0 ; 85 0 ; 900 0 ; 160 0 ; 100 0 ; 35 0 ; 60 0 ; 760 0 ; 45 0 ; 350 0 ; 360 0 ; 700 0 .
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

ГДЗ по математике 5 класс Зубарева, Мордкович
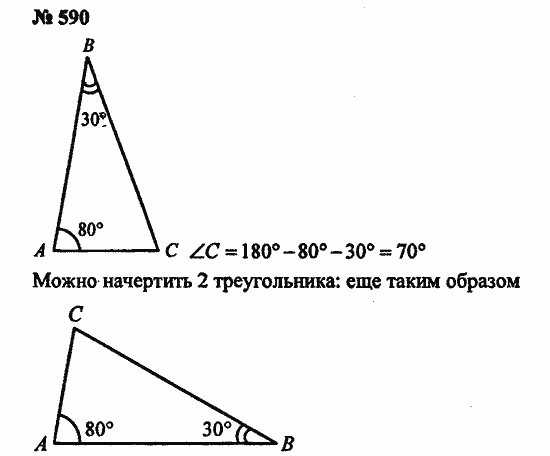
590. Начертите треугольник с углами 80° и 30°. Чему равен третий угол этого треугольника? Сколько неравных друг другу треугольников с такими углами можно начертить? ^3 = 180°- 30° — 80° = 70°.
Другое решение задачи №590:
Оцените это ГДЗ:
- Currently 2.55/5
- 1
- 2
- 3
- 4
- 5
Рейтинг: 2.5/5 (Всего оценок: 11)
Видео:№592. Постройте угол а, если:Скачать

Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Видео:Построение угла равного данномуСкачать

Числовая и единичная окружность
В средней школе мы уже познакомились с координатной, или числовой прямой. Так называют абстрактную прямую, на которой выбрана точка отсчета, определен единичный отрезок, а также задано направление, в котором следует откладывать положительные числа. С помощью координатной прямой удается наглядно представлять сложение и вычитание как положительных, так и отрицательных чисел, решать задачи, связанные с перемещением по прямой, и делать многое другое.
Однако порою приходится рассматривать задачи, связанные с движением по окружности, а также складывать и вычитать углы. Здесь математикам помогает другая абстракция – числовая окружность. Пусть два гонщика (Вася и Петя) едут по круговой трассе, чья протяженность составляет 1 км. За минуту Вася проехал 1250 м, а Петя преодолел только 500 м. Попытаемся показать их положение графически.
Построим на координатной плоскости окружность с центром в начале координат длиной 1 км. Будем считать, старт находится в крайней правой точке трассы, на пересечении оси Ох и окружности. Также условимся, что гонщики едут против часовой стрелки. Тогда получим такую картинку:
Петя проедет ровно половину окружности и окажется в крайней левой точке трассы. Вася же за минуту успел сделать полный круг (1 км) и проехать ещё 250 м, а потому оказался в верхней точке.
Теперь предположим, что Петя стоит на месте, а Вася проехал ещё 250 м (четверть круга). В результате оба пилота оказались в одной точке, но проехали они разное расстояние! Получается, что по положению гонщика невозможно однозначно определить, сколько именно метров он проехал.
Заметим, что очень удобно характеризовать положение точки на числовой окружности с помощью угла. Достаточно соединить точку отрезком с началом координат. Полученный отрезок образует с прямой Ох некоторый угол α:
В тригонометрии предпочитают использовать особую числовую прямую, радиус которой равен единице. По ряду причин, которые станут ясны чуть позже, с ней очень удобно работать. Такую фигуру называют единичной окружностью.
Выглядит единичная окружность так:
Видео:Углы, вписанные в окружность. Практическая часть. 9 класс.Скачать

Откладывание углов на единичной окружности
Положение каждой точки на единичной окружности можно указать с помощью угла. Пусть надо найти точку, соответствующую углу 60°. Для этого просто строим угол следующим образом:
Углы, которые откладывают на единичной окружности, называют углами поворота. В данном случае можно утверждать, что точке А соответствует угол поворота, равный 60°.
Отложить можно и угол, больший 90° и даже 180°. Выглядеть они будут примерно так:
Углы можно складывать друг с другом и вычитать. Предположим, нам надо построить угол, равный сумме углов 120° и 110°. Для этого сначала совершить поворот на 120°, а потом от полученного отрезка отложить ещё один угол в 110°:
Ясно, что возможно построить любой угол в диапазоне от 0° до 360°. А можно ли отложить угол, который будет больше 360°? В обычной планиметрии мы не работаем с такими углами, однако в тригонометрии они существуют. Действительно, мы же можем, например, сложить углы 250° и 140°. В итоге получится 250 + 140 = 390°:
В результате мы совершили полный оборот (360°) и вдобавок повернули отрезок ещё на 30°. Получается, что углам в 390° и 30° соответствует одна и та же точка.
Углы можно и вычитать друг из друга. Для этого вычитаемый угол надо отложить в противоположном направлении – не против часовой, а по часовой стрелке. Например, вычитая из 150° угол в 70°, придем в точку, соответствующую 150 – 70 = 80°:
Из арифметики мы помним, что вычитание можно заменить прибавлением противоположного (то есть отрицательного) числа:
Получается, что отложив угол 70° по часовой стрелке, мы прибавили к 150° отрицательный угол (– 70°). То есть на единичной окружности можно откладывать отрицательные углы! Для их получения поворот надо осуществлять по часовой стрелке. Например, угол – 60° будет выглядеть так:
Итак, мы можем откладывать и положительные, и отрицательные углы, а также углы, большие 360°. Вообще в тригонометрии угол может быть равен любому действительному числу. На единичной окружности можно отложить углы величиной 1000°, 1000000° и (– 999999999°) и любые другие, самые большие и самые малые углы. В этом смысле единичная окружность схожа с координатной прямой. Разница лишь в том, что на прямой разным числам всегда соответствуют разные точки, а на окружности разным углам могут соответствовать одни и те же точки.
Ещё раз отметим, что один полный оборот равен 360°. Если отложить на окружности произвольную точку А, которой соответствует угол α, а потом добавить к α ещё 360°, то мы попадем в ту же самую точку:
С точки зрения тригонометрии те углы поворота, которые соответствуют одной точке на единичной окружности, равны друг другу. Поэтому можно записать формулу:
Естественно, при вычитании 360° из угла мы тоже совершим полный поворот, только по часовой стрелке, поэтому верна и другая запись:
Угол, не изменится и в том случае, если мы совершим не один, а два полных оборота, то есть добавим к нему 2•360° = 720°. Можно добавлять к углу два, три, четыре полных поворота, но он не изменится от этого. Обозначим буквой n количество оборотов, которые мы добавляем к углу. Естественно, что n – целое число. Справедливой будет формула:
Например, верны следующие равенства:
15° + 3•360° = 15° + 1080° = 1095°
100° + 10•360° = 100° + 3600° = 3700°
1000° = 1000° – 2•360° = 1000° – 720° = 280°
Очевидно, что любой точке на окружности соответствует какой-то угол α из промежутка 0 ≤ α 1 5
🔍 Видео
Найти центр кругаСкачать

№155. С помощью циркуля и линейки постройте угол, равный: а) 45°; б) 22°30'.Скачать

Строим прямой уголСкачать

Построить угол , равный данному.Скачать

№590. Через точку сферы радиуса R, которая является границей данного шара, проведены две плоскостиСкачать

Углы, вписанные в окружность. Практическая часть. 9 класс.Скачать

Деление окружности на 12 равных частейСкачать

Построение угла, равного данному. 7 класс.Скачать

Радианная мера угла. 9 класс.Скачать

Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

1 2 4 сопряжение окружностейСкачать

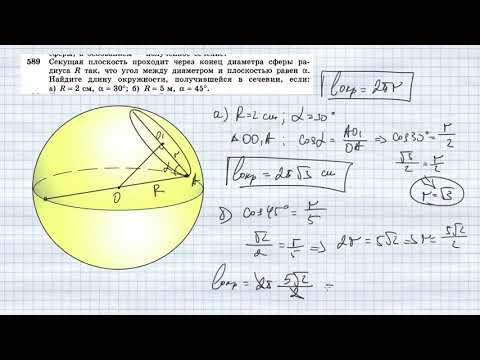
№589. Секущая плоскость проходит через конец диаметра сферы радиуса R так, что угол между диаметромСкачать
Вписанный угол, который опирается на диаметрСкачать
Построить прямой угол с помощью двусторонней линейки.Скачать

Задание №590 - ГДЗ по геометрии 7 класс (Мерзляк)Скачать