Курс школьной геометрии » Окружность

Постройте произвольный треугольник впишите в него окружность

Обновлено
Замечательные точки и линии треугольников. 9-й класс

Класс: 9

Содержание
  1. Презентация к уроку
  2. Треугольник вписанный в окружность
  3. Определение
  4. Формулы
  5. Радиус вписанной окружности в треугольник
  6. Радиус описанной окружности около треугольника
  7. Площадь треугольника
  8. Периметр треугольника
  9. Сторона треугольника
  10. Средняя линия треугольника
  11. Высота треугольника
  12. Свойства
  13. Доказательство
  14. Окружность, вписанная в треугольник
  15. Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
  16. Описание презентации по отдельным слайдам:
  17. Краткое описание документа:
  18. Дистанционное обучение как современный формат преподавания
  19. Математика: теория и методика преподавания в образовательной организации
  20. Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
  21. Дистанционные курсы для педагогов
  22. Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
  23. Другие материалы
  24. Вам будут интересны эти курсы:
  25. Оставьте свой комментарий
  26. Автор материала
  27. Дистанционные курсы для педагогов
  28. Подарочные сертификаты
  29. 💥 Видео

Презентация к уроку

Загрузить презентацию (529 кБ)

Цели:

  • Познакомить с замечательными точками и линиями треугольника;
  • познакомить с методами доказательства свойств замечательных точек и линий треугольника;
  • повторить и обобщить материал по теме «Треугольник».

Задачи развивающие:

  • Развитие умения устанавливать закономерности;
  • развитие умения формулировать гипотезы, опровергать ошибочные и доказывать истинные;
  • развитие умения составлять алгоритм действий и действовать по алгоритму;
  • развитие математической интуиции;
  • развитие графической культуры и математической речи.

Задачи воспитательные:

  • Повышение познавательного интереса;
  • расширение математического кругозора;
  • развитие навыка конструктивного группового взаимодействия независимо от многообразия проявлений индивидуальности;
  • воспитание чувства ответственности;
  • развитие умения выступать перед аудиторией

Тип урока: изучение нового материала.

Метод: проблемно-исследовательский.

Форма: групповая.

Ход урока

1. Организационный момент, объявление темы занятия (слайд 1).

2. Повторение.

Треугольник – фигура удивительная. Она удивляет своей простотой, лаконичностью и в то же время своей универсальностью. Вспомните сколько раз, чтобы решить задачу или доказать теорему мы прибегали к разбиению многоугольника на треугольники.

Треугольник – первая геометрическая фигура, изученная нами в курсе геометрии. И сегодня мы поговорим о новых для вас свойствах треугольника, а треугольник в свою очередь поможет вам повторить очень много изученных в курсе планиметрии тем.

Вспоминаем изученные замечательные точки треугольника:

  • Центр вписанной окружности (точка пересечения биссектрис треугольника);
  • Центр описанной окружности (точка пересечения серединных перпендикуляров к сторонам треугольника);
  • Точка пересечения высот треугольника (ортоцентр);
  • Точка пересечения медиан треугольника.

Также вспоминаем алгоритм построения с помощью циркуля и линейки
каждой из этих точек.

Каждая группа получает индивидуальное задание (приложение 1, задание 1).

Задание № 1. (группа 1)

С помощью циркуля и линейки построить окружность, описанную около треугольника (треугольник остроугольный, тупоугольный и прямоугольный).

Задание № 1. (группа 2)

С помощью циркуля и линейки построить окружность, вписанную в треугольник (треугольник остроугольный, тупоугольный и прямоугольный)

Задание № 1. (группа 3)

С помощью циркуля и линейки построить точку пересечения высот треугольника (треугольник остроугольный, тупоугольный и прямоугольный)

Задание № 1. (группа 4)

С помощью циркуля и линейки построить точку пересечения медиан треугольника (треугольник остроугольный, тупоугольный и прямоугольный)

(Для экономии времени, группы получают заготовленные на альбомных листах изображения треугольников; все построения выполняются фломастерами, циркуль – «козья ножка» также с фломастером).

После выполнения каждая группа демонстрирует свои результаты и комментирует построения. При необходимости учитель вносит дополнения (слайды 3 – 6).

3. Свойство точек, симметричных ортоцентру относительно сторон треугольника.

Как вы думаете, все ли закономерности, связанные с треугольником мы изучили? (приложение 1, задание 2).

Задание № 2.

  1. Постройте произвольную окружность.
  2. Впишите в него произвольный остроугольный треугольник АВС.
  3. Постройте высоты AA1, BB1, CC1. Пусть H — точка пересечения высот.
  4. Постройте точку А2, симметричную точке Н относительно прямой, содержащей сторону ВС.
  5. Постройте точку В2, симметричную точке Н относительно прямой, содержащей сторону АС.
  6. Постройте точку С2, симметричную точке Н относительно прямой, содержащей сторону АВ.

Какое свойство вы заметили?

Сформулируйте свойство точек, симметричных ортоцентру относительно сторон треугольника.

Задание № 2.

  1. Постройте произвольную окружность.
  2. Впишите в него произвольный тупоугольный треугольник АВС.
  3. Постройте высоты AA1, BB1, CC1. Пусть H — точка пересечения высот.
  4. Постройте точку А2, симметричную точке Н относительно прямой, содержащей сторону ВС.
  5. Постройте точку В2, симметричную точке Н относительно прямой, содержащей сторону АС.
  6. Постройте точку С2, симметричную точке Н относительно прямой, содержащей сторону АВ.

Какое свойство вы заметили?

Сформулируйте свойство точек, симметричных ортоцентру относительно сторон треугольника.

Проверяем выполнение задания. Формулируем свойство точек, симметричных ортоцентру относительно сторон треугольника. (Слайды 7, 9)

4. Продолжаем «открывать» новые точки и линии, связанные с геометрией треугольника.

1. А верите ли вы, что, если на сторонах треугольника построить равносторонние треугольники и около них описать окружности, то эти окружности пересекутся в одной точке? (слайд 11).

2. А верите ли вы, что, основания перпендикуляров, опущенных из любой точки окружности на три стороны вписанного в нее треугольника, лежат на одной прямой? (слайд 14).

3. А верите ли вы, что, в треугольнике середины его сторон, середины отрезков, соединяющих его вершины с его ортоцентром, и основания его высот лежат на одной окружности? (слайд 17).

4. А верите ли вы, что, в треугольнике центр описанной окружности, ортоцентр и центр тяжести лежат на одной прямой? (слайд 21).

5. Докажем рассмотренные нами свойства треугольника.

Каждая группа получает карточку с заданием и копию соответствующего слайда на электронном носителе (для экономии времени компьютеры, за которыми будут работать ребята, должны быть подготовлены заранее, фрагмент презентации загружен и выведен на экран). Карточка содержит формулировку задачи, ее доказательство и чертеж. Необходимо подготовить выступление по теме и привести доказательство утверждений, отмеченных значком. (Приложение 1. Задание 3).

Задание № 3 (группа 1)

На сторонах треугольника построены равносторонние треугольники и около них описаны окружности. Докажите, что эти окружности пересекутся в одной точке, называемой точкой Торричелли? Воспользуйтесь подсказкой и докажите утверждение, отмеченное значком «?».

Постройте произвольный треугольник впишите в него окружность

Задание № 3 (группа 2)

Докажите, что основания перпендикуляров, опущенных из любой точки окружности на три стороны вписанного в нее треугольника, лежать на одной прямой (прямая Симпсона)? Воспользуйтесь подсказкой и докажите утверждение, отмеченное значком «?».

Постройте произвольный треугольник впишите в него окружность

Задание № 3 (группа 3)

Докажите, в треугольнике середины его сторон, середины отрезков, соединяющих его вершины с его ортоцентром, и основания его высот лежат на одной окружности (окружность Эйлера)?

Воспользуйтесь подсказкой и докажите утверждения, отмеченные значком «?».

Постройте произвольный треугольник впишите в него окружность

Задание № 3 (группа 4)

Докажите, что в треугольнике центр описанной окружности, ортоцентр и центр тяжести лежат на одной прямой (прямая Эйлера)? (слайд 23)

Воспользуйтесь подсказкой и докажите утверждения, отмеченные значком «?».

Постройте произвольный треугольник впишите в него окружность

Проверяем выполнение задания. Каждая группа «представляет» свою замечательную точку или линию и доказывает связанное с ней утверждение (слайды 12 — 13, 15-16, 18-20, 22-24).

В качестве «сувенира», после доказательства каждой теоремы можно посмотреть соответствующие «созвездия» на «звездном небе» (слайды 28-31, к которым можно перейти с помощью кнопки «астроном», появляющейся, когда доказательство закончено).

Во время выступления слушатели должны отметить, какие теоремы из курса планиметрии за 7-9 классы используются для доказательства каждого утверждения и заполняют таблицу (Приложение 3).

После выступления группа строит соответствующую точку или прямую, выбирая наиболее подходящий чертеж. (Приложение 2.).

Учитель контролирует, при необходимости помогает выполнить построения. По завершении этого этапа работы еще раз проговариваем алгоритм построения.

6. Точки Фейербаха. (Слайды 25, 32)

Ну, и это еще не все!

Вернемся на минуту к окружности Эйлера.

Эта окружность, найденная в XVIII веке великим ученым А.Эйлером, была заново открыта в следующем столетии учителем провинциальной гимназии в Германии. Звали его Карл Фейербах. Он был родным братом известного философа Людвига Фейербаха. Дополнительно К.Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого треугольника. Это точки ее касания с четырьмя окружностями специального вида.

Одна из этих окружностей вписанная, остальные три – вневписанные. Они вписаны в углы треугольника и касаются внешним образом его сторон. Точки касания этих окружностей с окружностью девяти точек К1, К2, К3 и К – называются точками Фейербаха. Таким образом, окружность девяти точек является в действительности окружностью тринадцати точек.

Ну, и это еще не все!

7. Доказательство свойства точек, симметричных ортоцентру относительно сторон треугольника.

Теперь, вспомнив практически весь материал по теме «Треугольник» и не только (таблица 1), рассмотрев методы доказательств четырех теорем, связанных с геометрией треугольника, мы можем вернуться к вашему сегодняшнему «открытию» и попробовать доказать его самостоятельно.

Доказать свойство точек, симметричных ортоцентру относительно сторон треугольника.

(Группы работают самостоятельно при необходимой помощи учителя)

Наиболее успешное доказательство представляется классу, остальные группы вносят дополнения и замечания (слайды 8, 10, 26, 27)

Ну, и это еще не все!

8. Следствия:

1. Вернемся еще раз к окружности Эйлера: 1) радиус окружности Эйлера равен половине радиуса описанной окружности ∆АВС (слайд 33); 2) ∆АВH, ∆АСH, ∆ВСH имеют ту же окружность Эйлера, что и ∆АВС (слайд 34).

2. Вернемся к точке Торричелли – т.Ферма: 1) отрезки AA1. BB1 и СС1 пересекаются в точке Торричелли и равны между собой; и 2) если точка Торричелли М лежит внутри треугольника, то сумма расстояний от точки М до вершин треугольника MА+MВ+MС – минимальна (слайд 35).

(А в каком случае т.Торичелли не лежит внутри треугольника?)

3. Вернемся к прямой Симпсона: 1) точки F1, E1, D1 — симметричные точке Р относительно сторон ∆АВС, лежат на одной прямой F1D1; 2) прямая F1D1 проходит через ортоцентр Н ∆АВС; 3) прямая Симпсона делит отрезок РН пополам: РК = КН (слайд 36).

4. Вернемся к прямой Эйлера: 1) точка пересечения медиан делит отрезок ОН в отношении 1:2, считая от точки О; 2) центр окружности Эйлера т.N – лежит на прямой Эйлера и делит отрезок OH пополам (слайды 37).

А еще есть Точка Нагеля, точка Жергонна, точка Брокара, точка Лемуана…

9. Подведение итогов урока (обобщение нового материала, анализ работы групп).

Домашнее задание:

  1. Выясните, как расположены точки, симметричные ортоцентру относительно середин сторон треугольника. Сформулируйте теорему и докажите ее.
  2. Подготовьте экспресс-сообщение об ученом, чьим именем была названа точка или линия, свойство которой вы сегодня доказывали (Торричелли, Симпсон, Эйлер, Фейербах).

Литература:

  1. Е.Д. Куланин, С.Н.Федин «Геометрия треугольника в задачах», Москва, книжный дом «Либроком», 2009 г.
  2. И.М.Смирнова, В.А.Смирнов «Геометрия. Нестандартные и исследовательские задачи», учебное пособие 7 -11, Москва, Мнемозина, 2004 г.
  3. «Энциклопедический словарь юного математика», Москва, «Педагогика», 1989г.

Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Строим вписанную в данный треугольник окружность (Задача 2).

Треугольник вписанный в окружность

Постройте произвольный треугольник впишите в него окружность

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Окружность вписанная в треугольник и описанная около треугольника.

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Постройте произвольный треугольник впишите в него окружность

Видео:Построить описанную окружность (Задача 1)Скачать

Построить описанную окружность (Задача 1)

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

  1. Радиус вписанной окружности в треугольник,
    если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

  1. Радиус описанной окружности около треугольника,
    если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

  1. Площадь треугольника вписанного в окружность,
    если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

  1. Периметр треугольника вписанного в окружность,
    если известны все стороны:

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

  1. Сторона треугольника вписанного в окружность,
    если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

  1. Средняя линия треугольника вписанного
    в окружность, если известно основание:

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

  1. Высота треугольника вписанного в окружность,
    если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:4K Как вписать окружность в треугольник, inscribed circle for triangleСкачать

4K Как вписать окружность в треугольник, inscribed circle for triangle

Свойства

  • Центр вписанной в треугольник окружности
    находится на пересечении биссектрис.
  • В треугольник, вписанный в окружность,
    можно вписать окружность, причем только одну.
  • Для треугольника, вписанного в окружность,
    справедлива Теорема Синусов, Теорема Косинусов
    и Теорема Пифагора.
  • Центр описанной около треугольника окружности
    находится на пересечении серединных перпендикуляров.
  • Все вершины треугольника, вписанного
    в окружность, лежат на окружности.
  • Сумма всех углов треугольника — 180 градусов.
  • Площадь треугольника вокруг которого описана окружность, и
    треугольника, в который вписана окружность, можно найти по
    формуле Герона.

Видео:Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружность

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

Постройте произвольный треугольник впишите в него окружность

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

  1. Проведем серединные
    перпендикуляры — HO, FO, EO.
  2. O — точка пересечения серединных
    перпендикуляров равноудалена от
    всех вершин треугольника.
  3. Центр окружности — точка пересечения
    серединных перпендикуляров — около
    треугольника описана окружность — O,
    от центра окружности к вершинам можно
    провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Построить окружность, вписанную в треугольникСкачать

Построить окружность, вписанную в треугольник

Окружность, вписанная в треугольник

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Вписанная и описанная окружность - от bezbotvy

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Постройте произвольный треугольник впишите в него окружность

Постройте произвольный треугольник впишите в него окружность

Описание презентации по отдельным слайдам:

Постройте произвольный треугольник впишите в него окружность

Окружность, вписанная в треугольник

Постройте произвольный треугольник впишите в него окружность

Окружность называется вписанной в треугольник, если все стороны треугольника касаются окружности. A B C O

Постройте произвольный треугольник впишите в него окружность

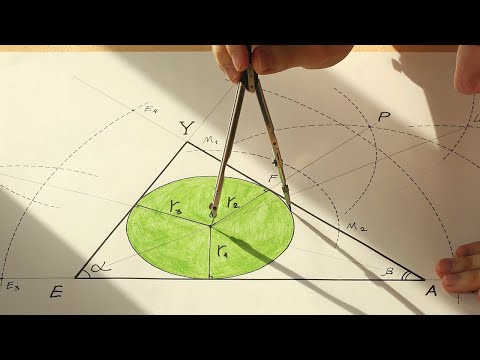
A B C D F E M N O K r r r Как вписать в окружность треугольник В треугольник можно вписать окружность, и притом только одну. Её центр – точка пересечения биссектрис треугольника. Проведём биссектрисы треугольника: АK, ВM, СN. Построим перпендикуляры ОD, OE, OF, которые равны между собой, т.к. равны соответствующие треугольники. Получаем ОD= OE= OF=r.

Постройте произвольный треугольник впишите в него окружность

Алгоритм построения вписанной окружности в треугольник 1.Строим две биссектрисы треугольника. Точка пересечения — центр вписанной окружности. 2. Строим перпендикуляр на основание из точки пересечения. 3. Этот перпендикуляр является радиусом вписанной окружности. 4. Строим вписанную окружность.

Постройте произвольный треугольник впишите в него окружность

Задача №1 Построить вписанную окружность в: 1. остроугольный треугольник; 2. тупоугольный треугольник; 3. прямоугольный треугольник. Самостоятельная работа Построить вписанную окружность в: 1. остроугольный равнобедренный треугольник; 2. тупоугольный равнобедренный треугольник; 3. прямоугольный равнобедренный треугольник.

Постройте произвольный треугольник впишите в него окружность

Положение центра вписанной окружности

Краткое описание документа:

Презентация по геометрии для урока в 8 классе создана для наглядного изучения вопроса о том, как вписать окружность в треугольник. В ней просто и доходчиво доказывается, что центром окружности, вписанной в треугольник, является точка пересечения биссектрис треугольника. Важная часть презентации — это то, что в ней показан алгоритм построения окружности, вписанной в треугольник. В презентации есть три задачи для закрепления нового материала. Также даны задачи для самостоятельной работы, решение которых поможет ребятам ещё лучше разобраться в новой теме. Последний слайд обращает внимание ребят на положение центра окружности, вписанной в треугольник.

Постройте произвольный треугольник впишите в него окружность

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

  • Сейчас обучается 954 человека из 80 регионов

Постройте произвольный треугольник впишите в него окружность

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

  • Сейчас обучается 684 человека из 75 регионов

Постройте произвольный треугольник впишите в него окружность

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

  • Сейчас обучается 309 человек из 67 регионов

Ищем педагогов в команду «Инфоурок»

Видео:№701. Начертите три треугольника: остроугольный, прямоугольный и тупоугольный. В каждыйСкачать

№701. Начертите три треугольника: остроугольный, прямоугольный и тупоугольный. В каждый

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 504 129 материалов в базе

Другие материалы

  • 13.05.2015
  • 3539
  • 8
  • 13.05.2015
  • 764
  • 0
  • 13.05.2015
  • 601
  • 0
  • 13.05.2015
  • 3374
  • 140
  • 13.05.2015
  • 1211
  • 1
  • 13.05.2015
  • 621
  • 5
  • 13.05.2015
  • 702
  • 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

  • 13.05.2015 6322
  • PPTX 227.7 кбайт
  • 6 скачиваний
  • Рейтинг: 5 из 5
  • Оцените материал:

Настоящий материал опубликован пользователем Сазонова Татьяна Фёдоровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

Постройте произвольный треугольник впишите в него окружность

  • На сайте: 7 лет
  • Подписчики: 0
  • Всего просмотров: 30363
  • Всего материалов: 17

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Описанная и вписанная окружности треугольника - 7 класс геометрияСкачать

Описанная и вписанная окружности треугольника - 7 класс геометрия

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Постройте произвольный треугольник впишите в него окружность

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Постройте произвольный треугольник впишите в него окружность

В Госдуме предложили создать в школах «ящики доверия» для обращений к психологу

Время чтения: 1 минута

Постройте произвольный треугольник впишите в него окружность

Санкт-Петербургский госуниверситет переходит на дистанционное обучение

Время чтения: 1 минута

Постройте произвольный треугольник впишите в него окружность

Большинство российских школьников недовольны качеством питания в столовых

Время чтения: 1 минута

Постройте произвольный треугольник впишите в него окружность

Минпросвещения намерено решить вопрос с третьей сменой в школах в 2023 году

Время чтения: 1 минута

Постройте произвольный треугольник впишите в него окружность

В Петербурге введут новые COVID-ограничения для несовершеннолетних

Время чтения: 2 минуты

Постройте произвольный треугольник впишите в него окружность

Новые курсы: педагогический дизайн, ФГОС 2021, управление школой и другие

Время чтения: 14 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

💥 Видео

Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Вписанная и описанная около равнобедренного треугольника, окружность

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.

№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать

№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. Для

Вписанный в окружность прямоугольный треугольник.Скачать

Вписанный в окружность прямоугольный треугольник.

Построение равностронего треугольника.Скачать

Построение равностронего треугольника.

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Вписанные и описанные окружности. Вебинар | Математика

Вписанная окружностьСкачать

Вписанная окружность

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnline

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Геометрия 8 класс (Урок№32 - Вписанная окружность.)

Как поделить окружность на 3 равные части. Очень просто. Уроки черчения.Скачать

Как поделить окружность на 3 равные части. Очень просто. Уроки черчения.

Вписанная окружность. ЗАДАЧА ИЗ ГОНКОНГА!Скачать

Вписанная окружность. ЗАДАЧА ИЗ ГОНКОНГА!
Поделиться или сохранить к себе: