Постройте биссектрису данного угла а данный угол проведем окружность (5 видео)

Как построить биссектрису данного угла? Задачи на построение

Существует такой забавный детский стишок, с помощью которого легко запомнить, что такое биссектриса: «Биссектриса — это такая крыса, что бегает по углам и делит угол пополам». Однако нельзя забывать, что, несмотря на простоту запоминания этого шуточного определения, учитель справедливо потребует другое, взятое из учебника.

В дальнейшем изучении школьной программы дети сталкиваются со сложной с первого взгляда задачей — как построить биссектрису данного угла с помощью циркуля. Однако уже более продвинутый школьник без труда справится с этим заданием, которое является основой выполнения цикла задач на построение в геометрии. Давайте же разберемся с этим вопросом раз и навсегда.

Содержание

Как построить биссектрису данного угла?
Алгоритм построения
Доказательство
Построить биссектрису данного угла
Геометрия 7 класс
ПРОШУ ПОМОГИТЕ
🎦 Видео

Видео:Построение биссектрисы углаСкачать

Как построить биссектрису данного угла?

Вам будет интересно: Французский язык: спряжение vivre

Самым очевидным и наиболее простым способом является использование транспортира, но если данного вспомогательного инструмента не оказалось под рукой, надо уметь строить биссектрису без него.

Для выполнения данной задачи, как уже понял читатель, нам потребуется циркуль, а помимо него — линейка (важно понимать, что делениями на ней пользоваться нельзя) и простой карандаш с ластиком.

Видео:Построение биссектрисы углаСкачать

Алгоритм построения

Необходимо совершить такие действия:

Установите иглу циркуля в вершине данного угла.

Установите циркулем произвольный радиус, проверните инструмент так, чтобы нарисованная им дуга пересекала оба луча, образующие угол.

Отметьте точки пересечения дуги со сторонами заданного угла.

Переставьте иглу циркуля в одну из отмеченных точек, выберете произвольный радиус и снова проверните циркуль таким образом, чтобы нарисованная им дуга была заключена внутри угла.

Аналогичные действия проделайте, передвинув циркуль в точку, отмеченную на другой стороне угла. Важно сохранить радиус, выбранный в предыдущем пункте алгоритма.

Отметьте точку пересечения двух дуг, которые были начерчены в двух предыдущих пунктах.

Проведите луч из вершины угла, проходящий через эту точку.

Полученный луч является искомым.

Мы дали ответ на поставленный вопрос — как построить биссектрису данного угла.

Видео:Построение биссектрисы угла. 7 класс.Скачать

Доказательство

Теперь, разобравшись, как построить биссектрису данного угла, стоит вспомнить еще одно определение биссектрисы, используя термин «геометрическое место точек». Биссектрисой называется геометрическое место точек, которые равноудалены от лучей, образующих угол.

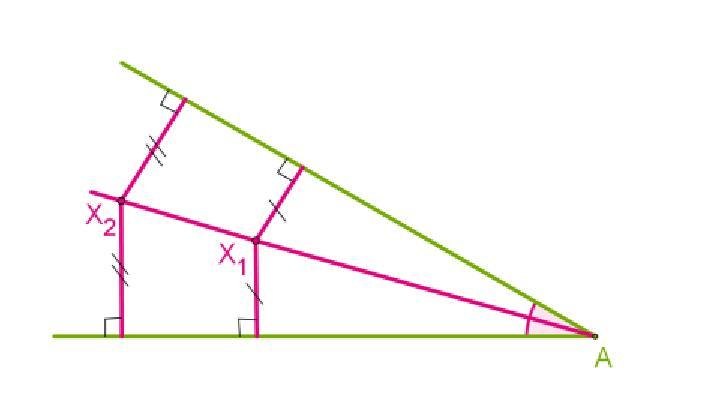
Согласно выполненному построению в пунктах 4-6, точка, принадлежащая построенной биссектрисе, также принадлежит двум окружностям, равным по радиусу, центр которых располагается на лучах, образующих угол на одинаковом расстоянии от вершины угла (согласно пунктам 1-3 построения). Опустим перпендикуляр из отмеченной в пункте 6 точки на лучи, образующие угол. Докажем, что получившиеся прямоугольные треугольники равны, и выясним, что опущенные перпендикуляры также равны, как соответствующие элементы треугольников. Таким образом, их общая гипотенуза является биссектрисой угла по определению. Что и требовалось доказать.

Видео:Построение угла, равного данному. 7 класс.Скачать

Построить биссектрису данного угла

Скачать
презентациюРассмотрим треугольники АСЕ и АВЕ >>

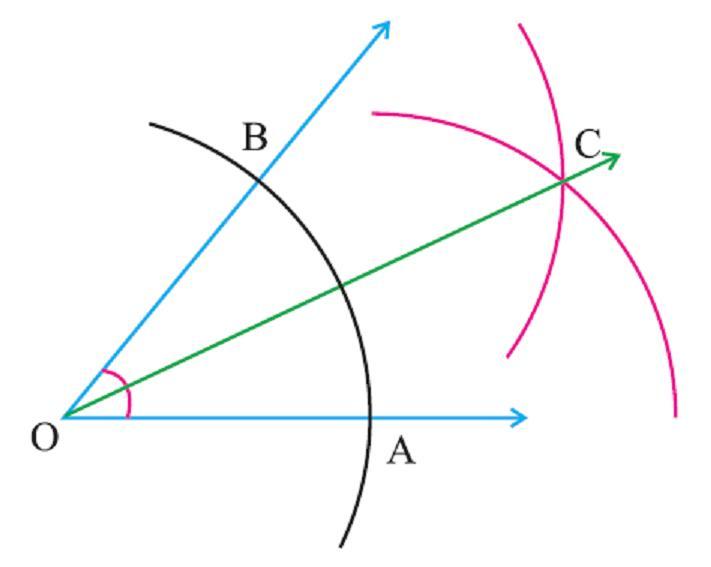
Задача. Построить биссектрису данного угла. Решение Данный угол ВАС изображен на рисунке. Проведем окружность произвольного радиуса с центром в вершине А. Она пересечет стороны угла в точках В и С. Затем проведем две окружности одинакового радиуса ВС с центрами в точках B и С. Они пересекутся в двух точках. Ту из этих точек, которая лежит внутри угла ВАС, обозначим буквой Е. Докажем, что луч АЕ является биссектрисой данного угла ВАС.

Слайд 9 из презентации «Геометрические задачи на построение». Размер архива с презентацией 2014 КБ.

Видео:Построение угла равного данномуСкачать

Геометрия 7 класс

«Начальные сведения геометрии» — Учёные- геометры. (Около 365-300 до н.э). Введение в геометрию. (1792-1856). Стереометрия. Взаимное расположение точек, прямой и отрезка. Оглавление. Евклид. Геометрические фигуры. Свойство прямой. (Около 570-500до н.э). Пифагор. Сколько точек пересечения могут иметь три прямые ? Планиметрия. Практические задания Взаимное расположение прямых на плоскости Практические задания. История возникновения геометрии.

«Параллельны ли прямые» — Рядом идущие. Вопросы. Папп. Посидоний. Замыкание. Способ построения. Свести параллели к схождению. Способ. Мужская голова. Определения параллельных прямых. Способ построения параллельных прямых. Николай Иванович Лобачевский. Недостаток информации. Построения параллельных прямых. Прямые, лежащие в одной плоскости. Параллельные прямые. Значимость параллельных прямых. Гипотеза. Аксиома параллельных прямых.

«1 признак равенства треугольников» — Равенство треугольников. Историческая справка. Какое еще условие должно быть выполнено. Треугольники, изображенные на рисунке. Ребусы. Треугольники АВС и ACD равны. Треугольники, изображенные на рисунке, равны. Треугольник. Треугольники равны. Первый признак равенства треугольников. Тестирование. Цели урока. Минутка отдыха. План урока. Самостоятельная работа. Найдите по рисунку величину угла АDС и длину стороны ВС.

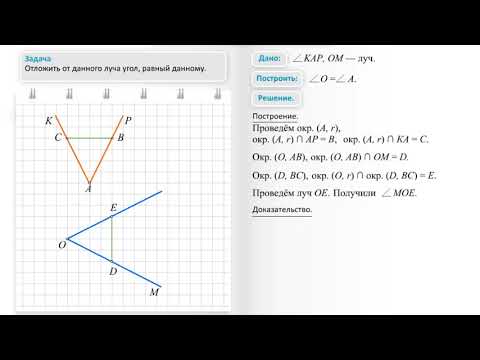
«Геометрические задачи на построение» — Отложить от данного луча угол, равный данному. Рассмотрим треугольники АВС и ОDЕ. Через вершину угла А и точку пересечения окружностей Е проведем прямую. Практические задания по группам. Построение перпендикулярных прямых. Строка параметров включает в себя кнопки состояния полей и сами поля. Медиана РМ равнобедренного треугольника. Построение прямоугольника в ручном режиме. Построить окружность с центром в точке В и с радиусом АВ.

«Свойства и признаки равнобедренного треугольника» — Установка. Равнобедренный треугольник. Медианы. Найдите угол. Девиз нашего урока. Биссектриса треугольника. Контрольные вопросы. Биссектрисы. Две стороны и угол между ними. Два перпендикуляра. Построение циркулем и линейкой. Понятие «свойство». Равносторонний треугольник. Треугольник. Высота. Углы при основании. Качество. Сумма углов треугольника. Исследовательская работа. Свойства треугольников. Достройте треугольник своего настроения.

««Измерение углов» 7 класс» — Измерение углов. Найдите угол, образованный биссектрисами углов. Лучи с общим началом в точке О. Луч OV является биссектрисой угла ZOY. Решение задач. Измерим величину угла АОВ. Свойства углов. Решение задач по готовым чертежам. Как строятся и измеряются углы с помощью транспортира. Виды углов.

Всего в теме «Геометрия 7 класс» 55 презентаций

Видео:Задачи на построение с помощью циркуля и линейки - 7 класс геометрияСкачать

ПРОШУ ПОМОГИТЕ

Построить биссектрису данного неразвёрнутого угла.

Добавьте пропуски в тексте решения задачи.

Пусть дан неразвёрнутый угол А.

Проведём окружность произвольного радиуса с центром _______и обозначим точки её пересечения со сторонами угла буквами _______и С. Затем построим две окружности радиуса _______ с центрами _______ и С.
Они пересекутся в двух точках. Ту из точек пересечения окружностей, которая лежит с точкой A по разные стороны от прямой BC, обозначим буквой _______. Наконец, проведём луч _______.Это и есть искомая биссектриса данного угла A.

Доказательство
В самом деле, треугольники ABD и _______равны по _______ (AB = _______, BD = _______, _______ ─ общая сторона). Поэтому ∠ BAD = ∠ _______, т.е. луч _______ ─ биссектриса угла _______.