- Планиметрия (прямая и окружность)
- 1.1 Построить угол 60° с заданой стороной
- 1.2 Построить серединный перпендикуляр к отрезку
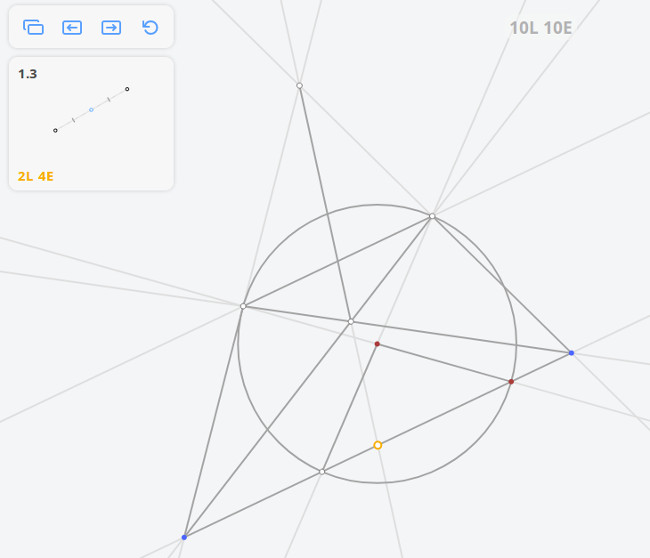
- 1.3 Середина отрезка
- 1.4 Окружность, вписанная в квадрат
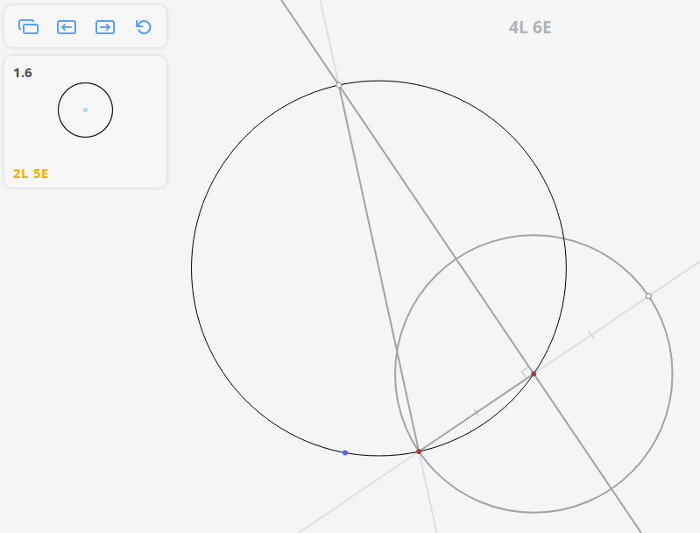
- 1.6 Найти центр окружности
- 1.7 Квадрат, вписанный в окружность
- Задача Наполеона
- Euclidea 1.1: Angle of 60°
- Euclidea 1.2: Perpendicular Bisector
- Euclidea 1.3: Midpoint
- Euclidea 1.4: Circle in Square
- Euclidea 1.5: Rhombus in Rectangle
- Euclidea 1.6: Circle Center
- Euclidea 1.7: Inscribed Square
- Euclidea 2.1: Angle Bissector
- Euclidea 2.2: Intersection of Angle Bisectors
- Euclidea 2.3: Angle of 30°
- Euclidea 2.4: Double Angle
- Euclidea 2.5: Cut Rectangle
- Euclidea 2.6: Drop a Perpendicular
- Euclidea 2.7: Erect a Perpendicular
- Euclidea 2.8: Tangent to Circle at Point
- Euclidea 2.9: Circle Tangent to Line
- Euclidea 2.10: Сircle in Rhombus
- Euclidea 3.1: Chord Midpoint
- Euclidea 3.2: Triangle by Angle and Orthocenter
- Euclidea 3.3: Intersection of Perpendicular Bisectors
- Euclidea 3.4: Three equal segments — 1
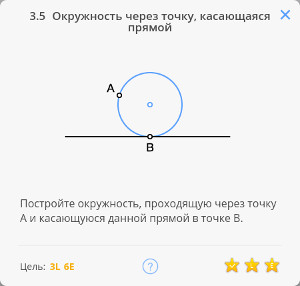
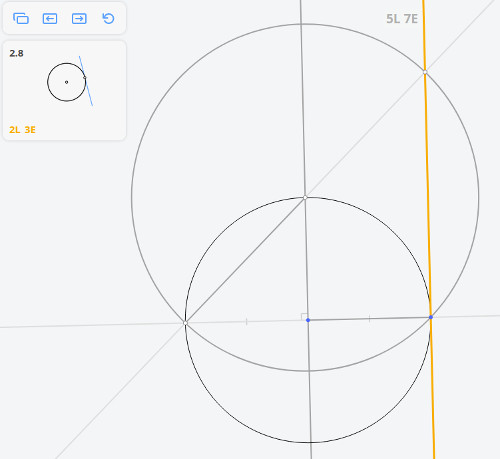
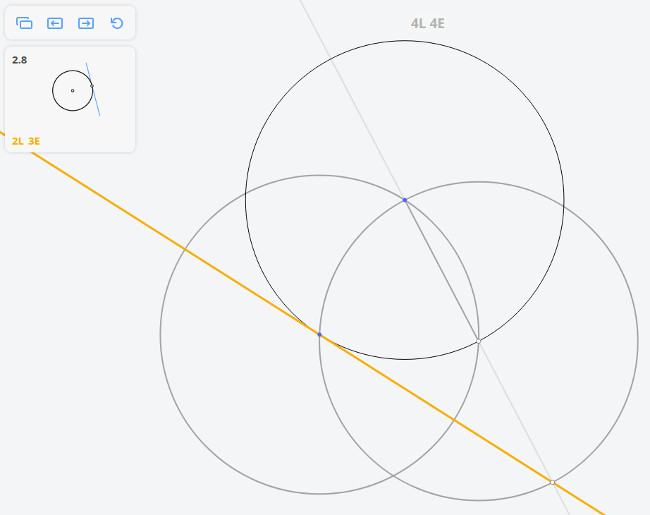
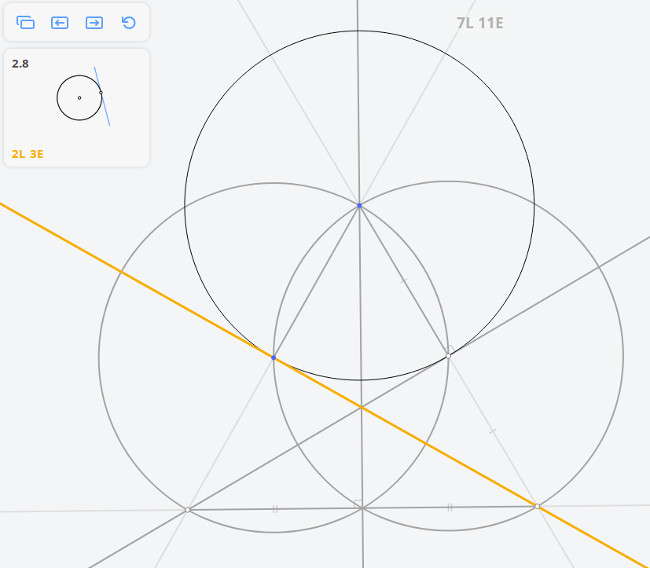
- Euclidea 3.5: Circle through Point Tangent to Line
- Euclidea 3.6: Midpoints Through Trapezoid Bases
- Euclidea 3.7: Angle of 45°
- Euclidea 3.8: Lozenge
- Euclidea 3.9: Center of Quadrilateral
- Euclidea 4.1: Double Segment
- Euclidea 4.2: Angle of 60° — 2
- Euclidea 4.3: Circumscribed Equilateral Triangle
- Euclidea 4.4: Equilateral Triangle in Circle
- Как построить центр окружности euclidea
- Euclidea: Типичные ошибки и заблуждения
- Euclidea: Подсказки и хитрости
- Euclidea: Предложения и пожелания
- Пифагория: Общие вопросы
- Пифагория: Подсказки
- Пифагория: Распространенные ошибки
- XSection: Общие вопросы
- XSection: Типичные заблуждения
- Как построить окружность?
- Планиметрия (прямая и окружность)
- 1.1 Построить угол 60° с заданой стороной
- 1.2 Построить серединный перпендикуляр к отрезку
- 1.3 Середина отрезка
- 1.4 Окружность, вписанная в квадрат
- 1.6 Найти центр окружности
- 1.7 Квадрат, вписанный в окружность
- Задача Наполеона
Видео:Быстро и легко определяем центр любой окружностиСкачать

Планиметрия (прямая и окружность)
Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).
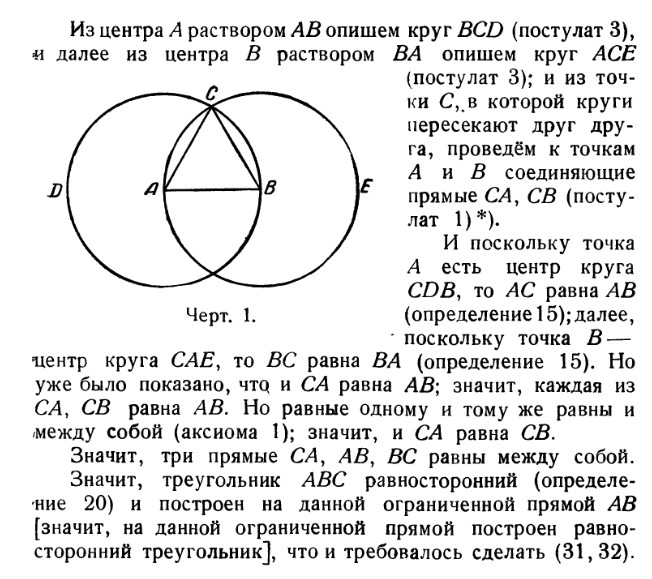
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
1.1 Построить угол 60° с заданой стороной
1.2 Построить серединный перпендикуляр к отрезку
На данной ограниченной прямой построить равносторонний треугольник
1.3 Середина отрезка
всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.
любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.
Решением задачи 1.3 по методу Штейнера-Понеселе будет:
1.4 Окружность, вписанная в квадрат
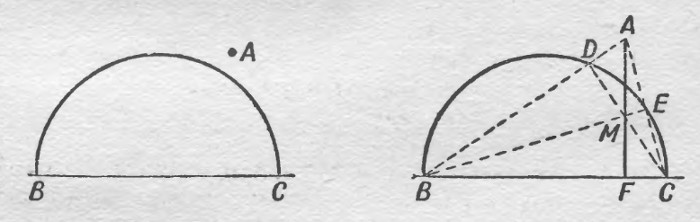
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.
Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.
И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой
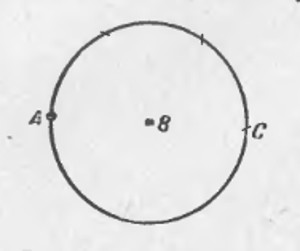
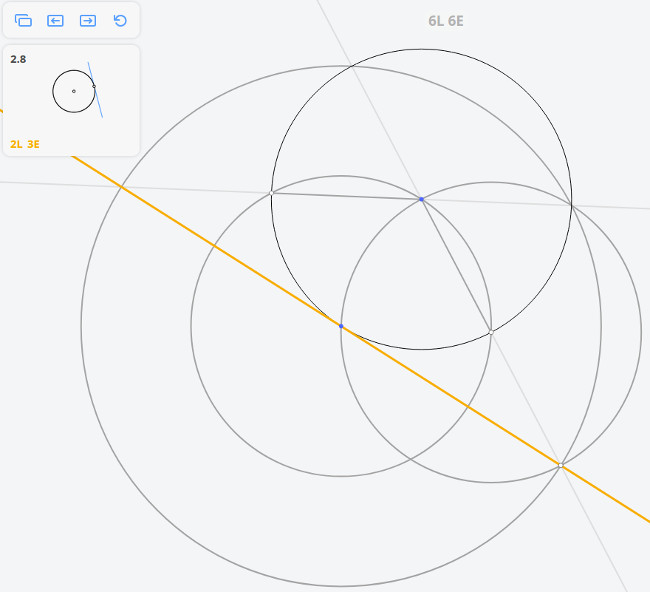
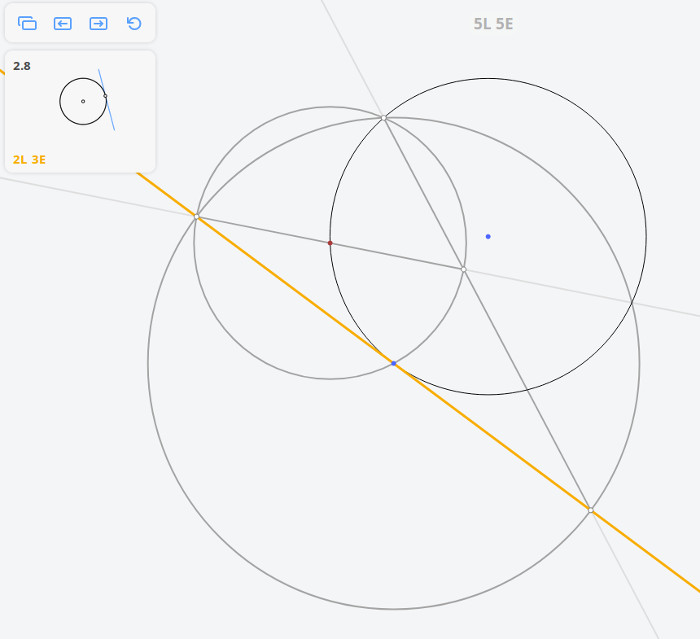
1.6 Найти центр окружности
Плоский угол, опирающийся на диаметр окружности, — прямой.
Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса
Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.
Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка
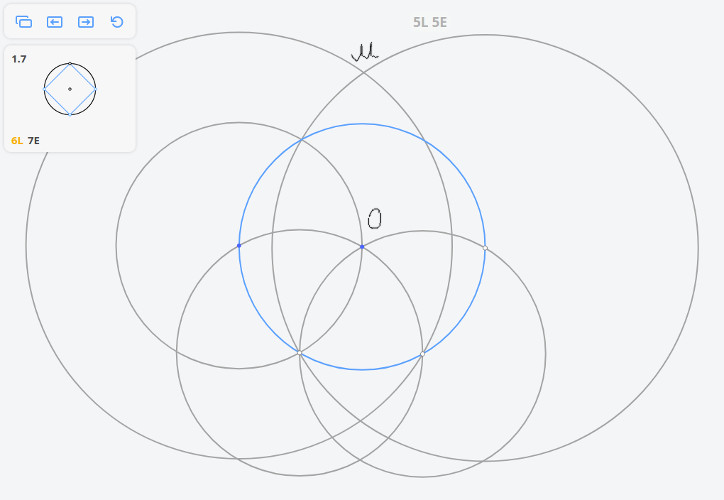
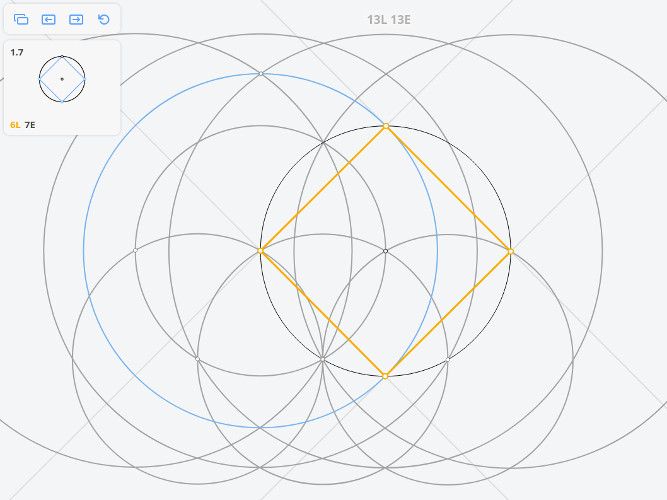
1.7 Квадрат, вписанный в окружность
Задача Наполеона
Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом
В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО
Видео:4K Как найти центр окружности, how to find the center of a circleСкачать

Euclidea 1.1: Angle of 60°
* A: given (-100.00,0.00)
* B: given (100.00,0.00)
circle: ⊙AB
circle: ⊙BA
* C = ⊙AB x ⊙BA (0.00,173.21)
line: (AC)
Видео:Как найти центр окружности с помощью циркуля и линейкиСкачать

Euclidea 1.2: Perpendicular Bisector
* A: given (-100.00,0.00)
* B: given (100.00,0.00)
circle: ⊙AB
circle: ⊙BA
* C = ⊙AB x ⊙BA (0.00,-173.21)
* D = ⊙AB x ⊙BA (0.00,173.21)
line: (CD)
Видео:Как найти центр круга с помощью подручных средств? ЛЕГКО.Скачать

Euclidea 1.3: Midpoint
* A: given (-100.00,-20.00)
* B: given (100.00,20.00)
line: (AB)
circle: ⊙AB
circle: ⊙BA
* C = ⊙AB x ⊙BA (34.64,-173.21)
* D = ⊙AB x ⊙BA (-34.64,173.21)
line: (CD)
* E = (AB) x (CD) (0.00,0.00)
Видео:Геометрия Задача найти центр круга /math and magicСкачать

Euclidea 1.4: Circle in Square
* A: given (-80.00,80.00)
* B: given (80.00,80.00)
circle: ⊙AB
circle: ⊙BA
* C: given (80.00,-80.00)
line: (AC)
* E = ⊙AB x ⊙BA (0.00,-58.56)
* F = ⊙AB x ⊙BA (0.00,218.56)
line: (EF)
* G = (AC) x (EF) (0.00,-0.00)
* H = (AB) x (EF) (0.00,80.00)
circle: ⊙GH
Видео:Как найти центр круга в мастерской (4 способа)Скачать

Euclidea 1.5: Rhombus in Rectangle
* B: given (81.12,33.99)
* C: given (81.12,-33.99)
circle: ⊙BC
* A: given (-81.12,33.99)
circle: ⊙BA
* E = (BC) x ⊙BC (81.12,101.96)
line: (AE)
* F = ⊙BA x (AE) (194.92,149.64)
line: (BF)
* D: given (-81.12,-33.99)
* G = ⊙BC x (AE) (32.67,81.66)
line: (DG)
Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

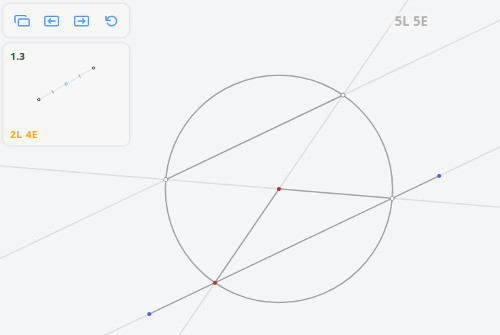
Euclidea 1.6: Circle Center
* B: given (135.81,63.68)
* C: given (142.58,-46.60)
circle: ⊙BC
circle: ⊙CB
* D = ⊙AB x ⊙BC (55.36,139.41)
circle: ⊙DB
* E = ⊙CB x ⊙DB (62.13,29.13)
line: (BE)
* F = ⊙BC x ⊙CB (43.69,2.68)
* G = ⊙BC x ⊙CB (234.70,14.40)
line: (FG)
* H = (BE) x (FG) (0.00,0.00)
Видео:Найти центр кругаСкачать

Euclidea 1.7: Inscribed Square
* B: given (0.00,150.00)
* A: given (0.00,0.00)
circle: ⊙BA
* C = ⊙AB x ⊙BA (129.90,75.00)
line: (AC)
* D = ⊙AB x ⊙BA (-129.90,75.00)
circle: ⊙CD
* E = ⊙AB x ⊙CD (0.00,-150.00)
* F = (AC) x ⊙CD (354.90,204.90)
line: (EF)
* G = ⊙AB x (EF) (150.00,0.00)
line: (BG)
* H = (AC) x ⊙CD (-95.10,-54.90)
line: (EH)
* I = ⊙AB x (EH) (-150.00,0.00)
line: (BI)
Видео:Найти центр и радиус окружностиСкачать

Euclidea 2.1: Angle Bissector
* A: given (0.00,0.00)
* B: given (150.00,0.00)
circle: ⊙AB
circle: ⊙BA
* D = (AC) x ⊙AB (102.07,109.92)
circle: ⊙DA
* E = ⊙BA x ⊙DA (252.07,109.92)
line: (AE)
Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Euclidea 2.2: Intersection of Angle Bisectors
* A: given (-120.00,-25.40)
* B: given (-5.54,123.00)
circle: ⊙AB
circle: ⊙BA
* D = (AC) x ⊙AB (67.34,-30.72)
circle: ⊙DA
* E = ⊙BA x ⊙DA (181.80,117.68)
line: (AE)
* F = (BC) x ⊙BA (145.92,12.62)
circle: ⊙FB
* G = ⊙AB x ⊙FB (31.46,-135.78)
line: (BG)
* H = (AE) x (BG) (7.07,34.84)
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Euclidea 2.3: Angle of 30°
* B: given (0.00,0.00)
* A: given (-150.00,0.00)
circle: ⊙BA
* C = (AB) x ⊙BA (150.00,0.00)
circle: ⊙CB
* D = ⊙BA x ⊙CB (75.00,129.90)
line: (AD)
Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Euclidea 2.4: Double Angle
* A: given (-150.00,0.00)
* B: given (0.00,0.00)
circle: ⊙AB
* D = (AC) x ⊙AB (-16.89,69.15)
circle: ⊙DB
* E = ⊙AB x ⊙DB (-63.75,122.72)
line: (AE)
Видео:Уравнение окружности (1)Скачать

Euclidea 2.5: Cut Rectangle
* B: given (81.12,33.99)
* D: given (-81.12,-33.99)
line: (BD)
* C: given (81.12,-33.99)
* A: given (-81.12,33.99)
line: (CA)
* E: given (152.10,146.78)
* F = (BD) x (CA) (-0.00,0.00)
line: (EF)
Видео:Как найти центр окружности с использованием только циркуля?Скачать

Euclidea 2.6: Drop a Perpendicular
* A: given (-100.00,0.00)
* C: given (0.00,79.00)
circle: ⊙AC
* B: given (-275.10,0.00)
circle: ⊙BC
* D = ⊙AC x ⊙BC (0.00,-79.00)
line: (CD)
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Euclidea 2.7: Erect a Perpendicular
* C: given (78.00,84.00)
* B: given (0.00,0.00)
circle: ⊙CB
* D = (AB) x ⊙CB (156.00,0.00)
line: (CD)
* E = ⊙CB x (CD) (0.00,168.00)
line: (BE)
Видео:Окружность и круг, 6 классСкачать

Euclidea 2.8: Tangent to Circle at Point
* C: given (144.61,39.83)
* B: given (83.88,124.36)
circle: ⊙CB
* D = ⊙AB x ⊙CB (135.72,-63.87)
circle: ⊙BD
* E = ⊙CB x ⊙BD (245.73,15.18)
line: (BE)
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Euclidea 2.9: Circle Tangent to Line
* A: given (112.00,0.00)
* C: given (0.00,125.00)
circle: ⊙AC
* D = (AB) x ⊙AC (-55.84,0.00)
circle: ⊙DC
* E = ⊙AC x ⊙DC (0.00,-125.00)
line: (CE)
* F = (AB) x (CE) (0.00,0.00)
circle: ⊙CF
Видео:Построить описанную окружность (Задача 1)Скачать

Euclidea 2.10: Сircle in Rhombus
* A: given (150.00,0.00)
* C: given (-150.00,0.00)
line: (AC)
* B: given (0.00,-122.20)
* D: given (0.00,122.20)
line: (BD)
* E = (AC) x (BD) (-0.00,0.00)
circle: ⊙AE
* F = (AB) x ⊙AE (266.29,94.74)
* G = (DA) x ⊙AE (33.71,94.74)
line: (FG)
* H = (BD) x (FG) (0.00,94.74)
circle: ⊙EH
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Euclidea 3.1: Chord Midpoint
* A: given (0.00,0.00)
* C: given (0.00,54.11)
line: (AC)
* B: given (111.00,126.90)
circle: ⊙BC
* D = (AC) x ⊙BC (-0.00,199.69)
line: (BD)
* E = ⊙BC x (BD) (222.00,54.11)
line: (CE)
Видео:Окружность. Круг. 5 класс.Скачать

Euclidea 3.2: Triangle by Angle and Orthocenter
* A: given (-120.23,10.00)
* D: given (87.00,56.00)
circle: ⊙AD
* B: given (145.00,0.00)
circle: ⊙BD
* E = ⊙AD x ⊙BD (82.95,-51.47)
line: (DE)
* C: given (109.70,176.30)
circle: ⊙CD
* F = ⊙AD x ⊙CD (-11.66,192.41)
line: (DF)
* G = (AC) x (DE) (91.03,162.79)
* H = (AB) x (DF) (127.01,0.68)
line: (GH)
Euclidea 3.3: Intersection of Perpendicular Bisectors
* D: given (87.00,56.00)
* A: given (-100.00,-12.30)
circle: ⊙DA
* E = (AB) x ⊙DA (279.35,4.67)
* F = (AC) x ⊙DA (167.69,238.00)
line: (EF)
Euclidea 3.4: Three equal segments — 1
* A: given (-100.00,31.30)
* D: given (97.00,65.00)
circle: ⊙AD
circle: ⊙DA
* E = ⊙AD x ⊙DA (27.69,-122.46)
* F = ⊙AD x ⊙DA (-30.69,218.76)
line: (EF)
* G = (AC) x (EF) (-7.92,85.67)
line: (DG)
circle: ⊙DG
* H = (AB) x ⊙DG (180.48,-1.83)
line: (DH)
Euclidea 3.5: Circle through Point Tangent to Line
* A: given (0.00,-100.00)
* C: given (-66.91,74.31)
circle: ⊙AC
circle: ⊙CA
* D = (AB) x ⊙CA (-133.83,-100.00)
line: (CD)
* E = ⊙CA x (CD) (-0.00,248.63)
line: (AE)
* F = ⊙AC x ⊙CA (117.50,45.11)
* G = ⊙AC x ⊙CA (-184.42,-70.79)
line: (FG)
* H = (AE) x (FG) (-0.00,0.00)
circle: ⊙HA
Euclidea 3.6: Midpoints Through Trapezoid Bases
* A: given (-22.40,76.00)
* C: given (75.10,-34.40)
line: (AC)
* B: given (68.40,76.00)
* D: given (-99.10,-34.40)
line: (BD)
* E: given (61.11,196.20)
* F = (AC) x (BD) (11.01,38.17)
line: (EF)
Euclidea 3.7: Angle of 45°
* A: given (0.00,0.00)
* B: given (100.00,0.00)
circle: ⊙AB
circle: ⊙BA
* C = ⊙AB x ⊙BA (50.00,-86.60)
line: (BC)
* D = ⊙BA x (BC) (150.00,86.60)
circle: ⊙DA
* E = (BC) x ⊙DA (236.60,236.60)
line: (AE)
Euclidea 3.8: Lozenge
* A: given (0.00,0.00)
* B: given (165.00,0.00)
circle: ⊙AB
circle: ⊙BA
* C = ⊙AB x ⊙BA (82.50,-142.89)
* D = ⊙AB x ⊙BA (82.50,142.89)
line: (CD)
* E = (AB) x (CD) (82.50,-0.00)
circle: ⊙EA
* F = (CD) x ⊙EA (82.50,82.50)
line: (AF)
* G = (CD) x ⊙EA (82.50,-82.50)
line: (BG)
* H = ⊙AB x (AF) (116.67,116.67)
* I = ⊙BA x (BG) (281.67,116.67)
line: (HI)
Euclidea 3.9: Center of Quadrilateral
* A: given (-201.00,124.00)
* B: given (176.00,199.00)
circle: ⊙AB
circle: ⊙BA
* E = ⊙AB x ⊙BA (52.45,-164.99)
* F = ⊙AB x ⊙BA (-77.45,487.99)
line: (EF)
* C: given (109.00,-76.00)
* D: given (-132.00,-120.00)
circle: ⊙CD
circle: ⊙DC
* G = ⊙CD x ⊙DC (-49.61,110.71)
* H = ⊙CD x ⊙DC (26.61,-306.71)
line: (GH)
* I = (AB) x (EF) (-12.50,161.50)
* J = (CD) x (GH) (-11.50,-98.00)
line: (IJ)
circle: ⊙IJ
circle: ⊙JI
* K = ⊙IJ x ⊙JI (-236.73,30.88)
* L = ⊙IJ x ⊙JI (212.73,32.62)
line: (KL)
* M = (IJ) x (KL) (-12.00,31.75)
Euclidea 4.1: Double Segment
* A: given (-100.00,0.00)
* B: given (0.00,0.00)
circle: ⊙AB
circle: ⊙BA
* C = ⊙AB x ⊙BA (-50.00,-86.60)
* D = ⊙AB x ⊙BA (-50.00,86.60)
circle: ⊙CD
* E = ⊙BA x ⊙CD (100.00,0.00)
Euclidea 4.2: Angle of 60° — 2
* B: given (123.12,0.00)
* C: given (0.00,121.24)
circle: ⊙BC
circle: ⊙CB
* D = (AB) x ⊙BC (295.92,0.00)
* E = ⊙BC x ⊙CB (166.56,167.25)
line: (DE)
* F = ⊙CB x (DE) (86.40,270.89)
line: (CF)
Euclidea 4.3: Circumscribed Equilateral Triangle
* A: given (0.00,0.00)
* B: given (100.00,0.00)
line: (AB)
* C = ⊙AB x (AB) (-100.00,0.00)
circle: ⊙CA
* D = ⊙AB x ⊙CA (-50.00,86.60)
* E = (AB) x ⊙CA (-200.00,0.00)
line: (DE)
* F = ⊙AB x ⊙CA (-50.00,-86.60)
line: (FE)
line: (AD)
* G = (FE) x (AD) (100.00,-173.21)
line: (BG)
Euclidea 4.4: Equilateral Triangle in Circle
Как построить центр окружности euclidea
В Euclidea нет встроенных решений. Проверяется не построение, а его результат.
Вероятно, ваше решение не принимается, поскольку оно приблизительное, то есть не является точным. Есть несколько способов это проверить:
Перечитайте условие задачи. Его можно посмотреть, нажав на карточку в левом верхнем углу экрана. Если вы забыли какое-нибудь определение, нажмите на знак вопроса, расположенный под условием.
Убедитесь, что искомый объект действительно построен. К примеру, вы могли забыть поставить точку на одном из концов отрезка.
Выберите инструмент «Перемещение» («Рука») и попробуйте подвигать разные точки. Решение должно удовлетворять условию задачи для любой конфигурации точек и фигур из условия.
Проверьте красные точки. Они не закреплены и их можно перемещать. В общем случае их не нужно избегать: некоторые оптимальные решения невозможны без красных точек. Однако стоит помнить, что, например, средняя точка или точка касания никогда не могут быть красными.
Войдите в режим Исследования (оранжевая кнопка) и посмотрите, как ответ зависит от конфигурации точек. Сравните это со своим решением.
Попробуйте доказать, что ваше построение удовлетворяет условию задачи. Визуального совпадения с правильным ответом недостаточно.
Если ничего не помогает, напишите нам, пожалуйста: support@euclidea.xyz.
Каждое решение оценивается в двух типах ходов: L (линии) и E (элементарные евклидовы построения). При этом построение точек не учитывается.
L подсчитывает действия инструментов: построение прямой, перпендикуляра, и так далее. E — количество ходов, как если бы построение делалось только с помощью настоящих циркуля и линейки. Каждый продвинутый инструмент имеет свою условную Е цену (см. таблицу).
Целью является решение задачи за наименьшее количество ходов. L и E цели могут достигаться независимо. Многие задачи имеют универсальное решение, удовлетворяющее обеим целям. Но некоторые задачи придётся решить дважды: одно решение, чтобы достигнуть L цели, второе — для E цели.
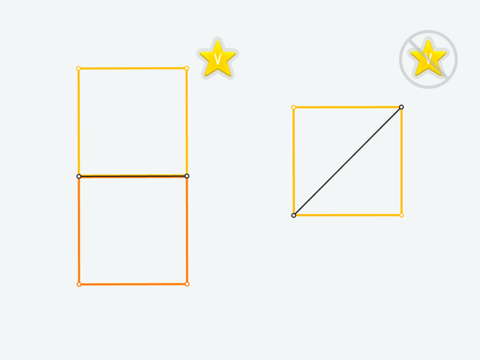
Если условию задачи удовлетворяет несколько фигур, вы можете получить скрытую V-звезду, построив их все на одном экране. Например, по заданной стороне можно построить два квадрата (V-звезда доступна), а если изначально дана диагональ, то квадрат определяется единственным образом (V-звезды нет). Обычно дополнительные решения получаются простым отражением или подразумевают некую симметрию.
Полезные подсказки:
Внимательно читайте формулировку задачи. Например, если в ней упоминается диагональ, рассмотрите варианты использования разных диагоналей.
Проверьте точки пересечения, на которых основано ваше построение. Например, окружность может пересекать прямую или другую окружность в двух точках. Если одна из этих точек используется при построении следующих фигур, попробуйте использовать для этого и вторую.
У некоторых задач может быть 3 или даже 4 ответа. Если вторая фигура принимается (подсвечена оранжевым), но V-звезда не дается, значит нужно продолжить поиск других ответов и достроить их.
В игре есть подсказки про V-звёзды. Они показывают количество ответов в текущем уровне. Откройте меню в правом верхнем углу игрового экрана (три горизонтальные линии), нажмите на «Лампочку» и выберите подсказку «V-звезда».
Нажмите на кнопку для вызова меню в правом верхнем углу игрового экрана, затем на стрелку вправо.
Чтобы переключить язык в игре:
- Нажмите на шестерёнку на главном экране.
- В открывшемся диалоге выберите второй пункт.
- Выберите нужный язык в списке и нажмите на нижнюю кнопку, чтобы его применить.
Вы можете переносить свой игровой прогресс (полученные звёзды и сохраненные решения задач) между устройствами, используя учетную запись Euclidea. Авторизуйтесь, чтобы не потерять свои результаты.
Euclidea — это игра, соревнование. Наша цель — пробудить у людей желание изучать геометрию.
Euclidea не хочет лишать своих пользователей удовольствия самостоятельно найти решение. Поэтому мы не предоставляем готовых ответов к задачам, а только даём подсказки.
Если вы хотите продолжить игру без совершения встроенной покупки, необходимо собрать все звёзды в первых двух разделах. Пожалуйста, проверьте, что у вас всего 74 звезды. (См. Как найти скрытые V-звёзды?)
Примечание. После покупки звёзды перестают учитываться, и задачи открываются одна за другой по мере их решения. Можно также пропустить любую задачу.
Есть несколько способов играть в Euclidea бесплатно.
На мобильном устройстве (телефоне или планшете) с iOS либо Android:
- Решать каждую задачу на максимальный балл. Вы можете пройти всю игру, если получаете все звёзды (L, E и V). Это трудно, но возможно.
- Если у вас нет возможности приобрести встроенную покупку, снимающую это ограничение, но вы любите геометрию, то можно попросить промокод в нашей группе ВКонтакте. Там также помогут с решением задач, если они не поддаются.
- Играйте в браузерную версию Euclidea. В ней не надо собирать все звёзды, чтобы пройти дальше. Новые задачи открываются по мере решения предыдущих.
Android: Чтобы выйти из приложения Euclidea, используйте системную кнопку «назад». Если виртуальные кнопки скрыты, проведите пальцем вверх от нижнего края экрана для вызова панели навигации.
Точки не учитываются. Любой другой инструмент, порождающий прямую или окружность, стоит 1L. E-цена индивидуальна:
Подсказка. E-цена выбранного инструмента отображается в левом верхнем углу кнопки в виде маленьких точек.
Циркуль Евклида «схлопывался», отрываясь от чертежа. В Euclidea ему соответствует инструмент «Окружность». Циркуль, сохраняющий расстояние, тоже есть, он появляется в разделе Дзета.
Покупки восстанавливаются автоматически, если вы используете тот же Google аккаунт или Apple ID. Т.е. после прохождения паков Альфа и Бета, пак Гамма должен разблокироваться автоматически. Если вы используете другой аккаунт, то покупка не восстановится.
iOS: Чтобы восстановить покупки выберите «Настройки» -> «Покупки» -> «Восстановить покупки».
Euclidea: Типичные ошибки и заблуждения
Распространённой ошибкой в обучающем уровне «Равносторонний треугольник» является построение окружностей на глаз.
Выберите инструмент «Перемещение» («Рука») и убедитесь, что ваше построение не содержит красные точки. Красным помечаются точки, которые не являются фиксированными и могут быть перемещены.
Чтобы пройти этот уровень, при построении окружности следует провести пальцем от центра до второй точки так, чтобы она «прилипла».
Точное построение
Приближенное построение
Пунктирная линия является только декорацией инструмента «Серединный перпендикуляр», и для построений её нельзя использовать.
Неправильное построение
Красная точка не закреплена, её можно перемещать.
Напомним, что ромб — это четырёхугольник, у которого все стороны равны.
Общей ошибкой в уровне «Ромб, вписанный в прямоугольник» является предположение, что угол ромба равен 60 градусам.
Чтобы проверить правильность своего построения, выберите инструмент «Перемещение» («Рука») и подвигайте левую верхнюю вершину прямоугольника. Правильное построение должно быть устойчивым к подобным трансформациям, и ромб должен оставаться ромбом.
Для решения этой задачи вспомните, что диагональ ромба — серединный перпендикуляр к другой диагонали.
Пример неправильного построения
В задаче «Квадрат, вписанный в окружность» данная точка, лежащая на окружности, должна быть одной из вершин квадрата.
Пример неправильного построения
Чтобы проверить правильность своего построения в уровне 2.5 «Разрезание прямоугольника»:
- Включите режим Исследования с помощью оранжевой кнопки в правом нижнем углу экрана (в нем отображаются искомые объекты).
- Повторите свои построения.
- Выберите инструмент «Перемещение» («Рука») и подвигайте левую верхнюю вершину прямоугольника.
Правильное построение должно совпадать с ответом (оранжевая прямая) при любой конфигурации точек и фигур.
Ключ к решению этой задачи легко найти, заметив закономерность движения оранжевой прямой (ответа) при перемещении заданной точки в режиме Исследования.
Пример неправильного построения
Euclidea: Подсказки и хитрости
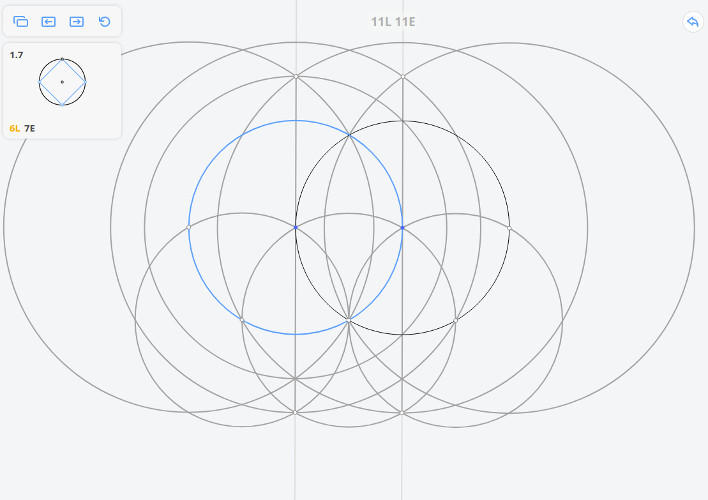
Чтобы получить 3 звезды в задаче 1.6 «Центр окружности», нужно её решить два раза — одно решение за 2L (две линии) для L-звезды, а другое за 5E (пять элементарных построений — окружностей или прямых) для E-звезды.
L и E цели являются независимыми, хотя у некоторых задач существуют универсальные решения, за которые можно получить сразу три звезды.
Чтобы найти решение 5E для задачи 1.6 «Центр окружности», попробуйте построить 2 серединных перпендикуляра с помощью окружностей и прямых. Затем останется понять, как сэкономить одну окружность. Последовательность инструментов — OOO// (3 окружности и 2 прямые).
Задача 1.7 «Квадрат, вписанный в окружность» может быть решена с помощью следующей последовательности инструментов: OO///// (2 окружности и 5 прямых). Попробуйте проанализировать, как именно надо построить эти линии.
- Первая окружность — единственно возможная.
- Вторая окружность позволяет получить нижнюю вершину искомого квадрата.
- Последние 4 прямые — стороны квадрата.
Остаётся понять, как построить третью прямую, чтобы получить ещё полезные точки. Экспериментировать удобно в режиме Исследования (оранжевая иконка), в котором отображаются искомые объекты.
Прием, используемый для оптимизации решения задачи 2.2, аналогичен примененному в уровне 1.6 («Центр окружности»). Две биссектрисы строятся с помощью окружностей и прямых, но некоторые окружности используются повторно, сокращая количество ходов. В частности, все 4 окружности оказываются одного радиуса.
Чтобы решить задачу 2.6 «Опустить перпендикуляр» за 3Е, постройте точку, симметричную данной относительно прямой (2 окружности). Затем соедините точки.
Для решения задачи 2.7 «Восстановить перпендикуляр» за 3E можно заметить, что вписанный угол, опирающийся на диаметр, является прямым. Последовательность инструментов: O// (окружность и 2 прямые).
Чтобы решить задачу 2.7 «Восстановить перпендикуляр» за один ход, вам понадобится всего один единственный инструмент. Обратите внимание, что 180 / 2 = 90.
Задача 2.8 «Касательная к окружности в точке» может быть решена с помощью следующей последовательности инструментов: OO/ (2 окружности и прямая). Примечательно, что для этого решения не нужен центр окружности.
Чтобы решить задачу 4.1 «Удвоенный отрезок», пользуясь только циркулем, необходимо построить 3 окружности. Первые 2 окружности — единственно возможные. Остаётся понять, как построить третью окружность, чтобы получить в пересечении искомую точку.
Последовательность инструментов для решения: OOА (2 окружности и биссектриса). Последний шаг даст вам ключ к первым двум. Обратите внимание, что не всякая точка подходит в качестве центра первой окружности. В частности, она не лежит на заданном луче.
Задача о трисекции угла в общем случае неразрешима. Поэтому нужно воспользоваться одним из равенств:
- 54 / 3 = 18
- 90 — 54 = 36 = 2 * 18
Euclidea: Предложения и пожелания
Сейчас Euclidea доступна на следующих языках:
- английский
- русский
- французский
- немецкий
- итальянский
- испанский
- португальский (Бразилия)
- греческий
- японский
- корейский
- упрощенный китайский
- голландский
- украинский
- польский
- словацкий
Если вы хотите помочь с переводом на другие языки, пожалуйста, напишите нам на support@euclidea.xyz.
Мы рассматривали возможность добавить отдельный режим для свободного рисования, однако пришли к выводу, что в игре это будет выглядеть неуместно. Поэтому мы решили сделать отдельное приложение, основанное на Euclidea, где можно было бы выполнять произвольные построения, сохранять их, изменять стили линий и т.д.
iOS: Встречайте Euclidea: Sketches.
Мы не планируем добавлять в игру инструмент, стирающий линии.
Пифагория: Общие вопросы
Чтобы пропустить уровень в Пифагории и Пифагории 60°, несколько раз нажмите на кнопку Вперед (стрелка вправо), пока она не заполнится цветом. Можно посмотреть видео в нашем Instagram. С каждым разом количество нажатий для пропуска будет увеличиваться, так что не злоупотребляйте.
Пифагория: Подсказки
Чтобы пройти уровень 1.13, попробуйте построить вспомогательную прямую, которая проходила бы через середину данного отрезка.
Например, это может быть вертикальная линия — серединный перпендикуляр отрезка (для его построения тоже потребуются дополнительные линии, как в задаче 1.12).
Задача со звёздочкой: решить 1.13 с помощью всего одной дополнительной прямой.
Есть несколько способов решить задачу 2.19.
Например, можно подобрать такой треугольник с вершинами в узлах сетки, чтобы одна его сторона лежала на заданной прямой, данная точка была серединой второй стороны, и можно было легко найти середину третьей. Средняя линия такого треугольника будет ответом к задаче.
Пифагория: Распространенные ошибки
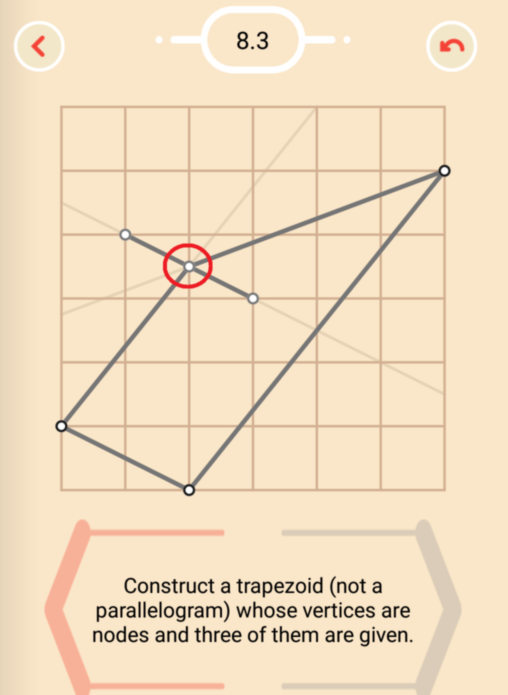
Вершины искомой трапеции в задаче 8.3 должны находиться в узлах сетки, то есть в точках пересечения линий сетки. Чтобы посмотреть определения в глоссарии, нажмите кнопку «i» на игровом экране.
XSection: Общие вопросы
XSection на Android мы выпустили позднее iOS версии и реализовали в нем несколько новых идей. Дизайн приложения был полностью обновлен, а задачи распределены по-новому.
Обновление XSection для iOS пока не планируется.
XSection: Типичные заблуждения
В задаче 9.5 нет ошибки. В диагональном сечении куба прямоугольник, а не квадрат, и его диагонали не перпендикулярны. Это заблуждение очень популярно у наших пользователей, поэтому мы специально выложили визуализацию таких сечений куба.
Как построить окружность?
Как построить окружность?
Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.
Радиусом называется любой отрезок соединяющей точку окружности с ее центром.
Чтобы построить окружность необходимо знать уравнение окружности:
(х – а) 2 + (у – b) 2 = R 2
Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.
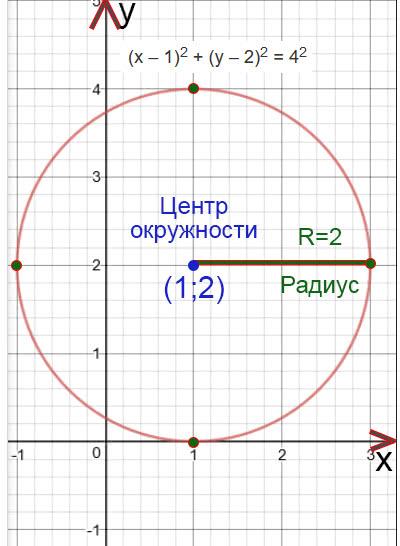
И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:
Пример №1:
(х – 1) 2 + (у – 2) 2 = 4 2
Найдем центр окружности:
х – 1=0
x=1
Центр окружности будет находится в точке (1;2)
Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2
Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.
Пример №2:
х 2 + (у + 1) 2 =1
Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2
Найдем центр окружности:
х=0
Центр окружности будет находится в точке (0;–1)
Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1
Построим окружность.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Планиметрия (прямая и окружность)
Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
1.1 Построить угол 60° с заданой стороной
1.2 Построить серединный перпендикуляр к отрезку
На данной ограниченной прямой построить равносторонний треугольник
1.3 Середина отрезка
всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.
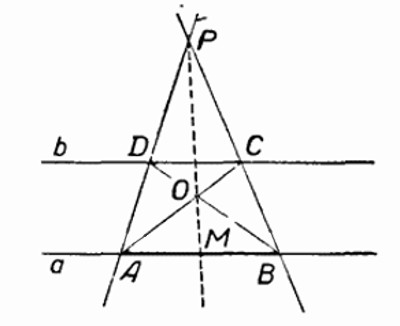
любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.
Решением задачи 1.3 по методу Штейнера-Понеселе будет:
1.4 Окружность, вписанная в квадрат
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.
Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.
И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой
1.6 Найти центр окружности
Плоский угол, опирающийся на диаметр окружности, — прямой.
Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса
Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.
Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка
1.7 Квадрат, вписанный в окружность
Задача Наполеона
Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом
В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО