Построить треугольник в окружности как равносторонний с заданной стороной (3 видео)

Как начертить равносторонний треугольник

Из этого материала вы узнаете, как с помощью циркуля построить правильный треугольник. Напомним, что треугольник является правильным, если длина всех его сторон одинакова, а каждый из углов составляет 60°.

На листе бумаги отметьте произвольную точку. Установите в эту точку иглу циркуля и нарисуйте окружность.

Установите иглу циркуля в любую произвольную точку, лежащую на окружности, и нарисуйте вторую окружность с центром в этой точке.

При этом не меняйте раствор циркуля, то есть радиус первой окружности должен быть равен радиусу второй окружности.

Отметьте точки пересечения окружностей.

Соедините полученные точки линией. Полученный отрезок будет первой стороной треугольника.

Далее, через центры обеих окружностей нужно провести прямую линию.

Таким образом, у вас получилось три точки, которые будут тремя вершинами треугольника.

Соедините все три точки между собой.

Полученный треугольник имеет одинаковую длину сторон, а величина каждого его угла составляет 60°, а значит он правильный.

Видео:Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Техническое черчение. Построение правильных многоугольников.

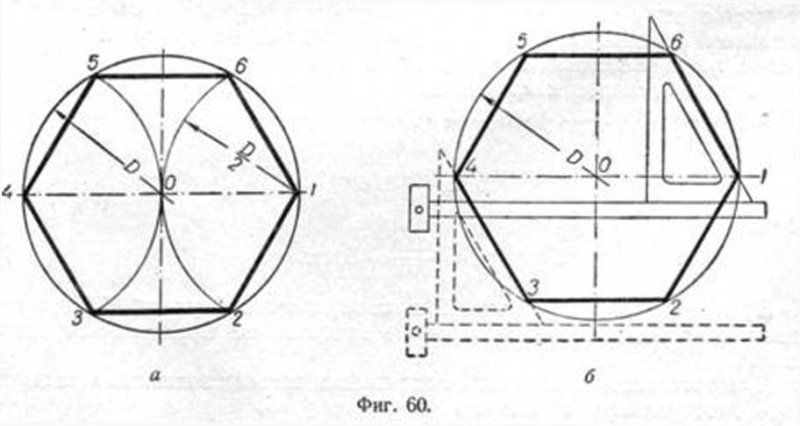
Построить треугольник в окружности как равносторонний с заданной стороной

Построение вписанного в окружность правильного шестиугольника.

Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой.

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4, строим стороны 1 — 6, 4 — 3, 4 — 5 и 7 — 2, после чего проводим стороны 5 — 6 и 3 — 2.

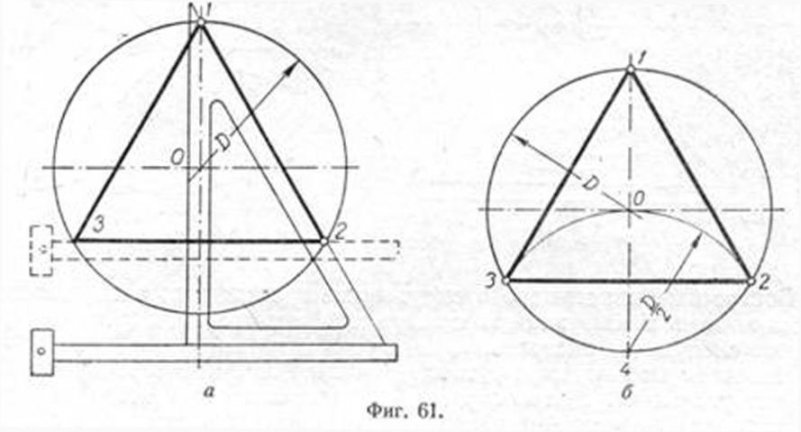
Построение вписанного в окружность равностороннего треугольника.

Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0 — 1 — 2 равен 30°, то для нахождения стороны 1 — 2 достаточно построить по точке 1 и стороне 0 — 1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1 — 2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2 — 3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.

Для построения треугольника намечаем на диаметре вершину точку 1 и проводим диаметральную линию 1 — 4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

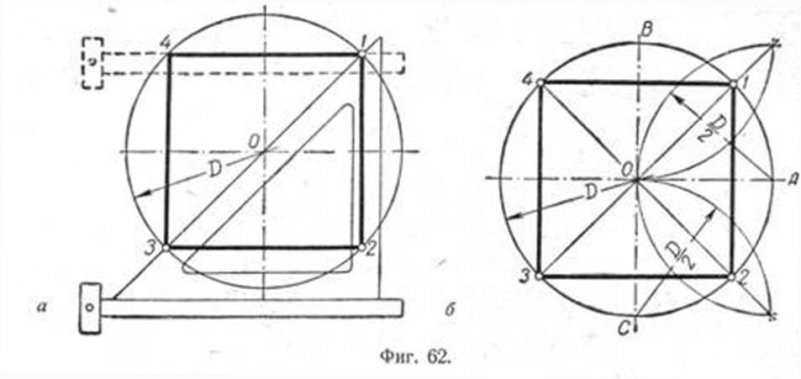
Построение квадрата, вписанного в окружность.

Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4 — 1 и 3 —2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1 — 2 и 4 — 3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра. Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

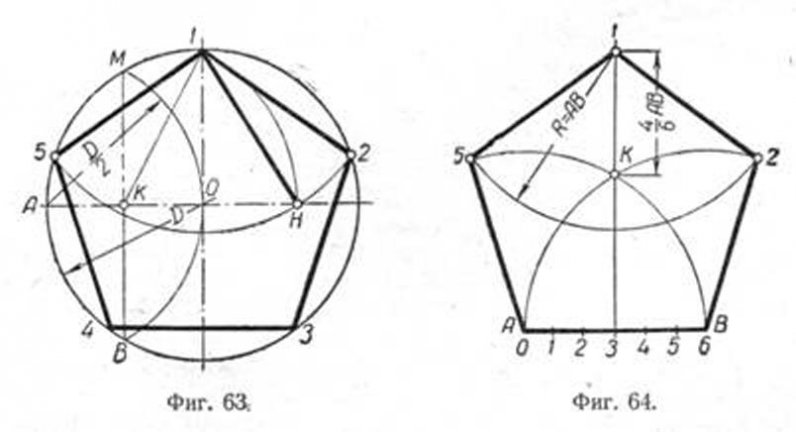
Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник, производим следующие построения. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую. Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB. Получим точку 1 —вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

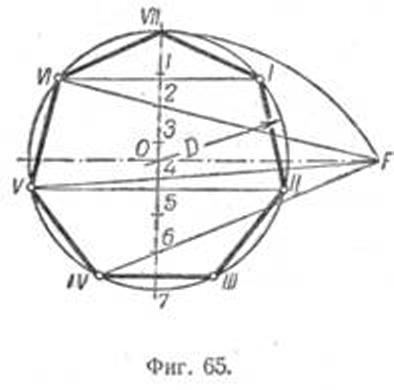
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

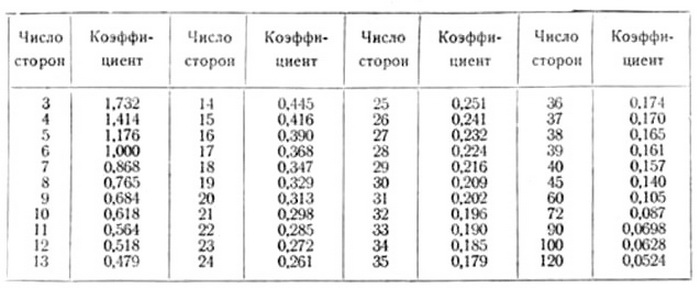
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

Длины сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй — коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Видео:Построение пятиугольника с заданной стороной циркулемСкачать

Построение

Построение правильного треугольника

Способ 1. Начертим окружность с центром в точке O, проведем диаметр ED. Обозначим на нем точку K так, что OK=KD. Теперь проведем через точку K хорду MN, перпендикулярную OD. Соединим точки E, M и N. Полученный треугольник EMN — равносторонний.

Способ 2. Начертим окружность с центром O и радиусом OA. Начертим вторую окружность с таким же радиусом, проходящую через точку O. Соединим центры этих окружностей и одну из точек пересечения (в данном случае с точкой B). Полученный треугольник — равносторонний.

Способ 3. Построим окружность с центром O. Далее построим некоторую точку, принадлежащую окружности. Из данной точки на окружность раствором циркуля, равным R, откладываем последовательно отрезки (их 6). Полученные точки соединяем через 1.

Способ 4. Строим окружность произвольного радиуса, с центром в точке А. Проводим прямую, через точку А. Отмечаем точки пересечения прямой и окружности С и В. Строим вторую окружность, с радиусом, равным радиусу, первой окружности и центром в точке С. Отмечаем точки пересечения окружностей F и D. Соединяем точки В,D,F. Треугольник BDF — равносторонний.

Построение правильного четырехугольника (квадрата)

Способ 1 (рис. 1). Проводим в окружности 2 перпендикулярных диаметра (Шаг 1). Точки пересечения этих диаметров с окружностью являются вершинами квадрата (Шаг 2).

Способ 2 (рис. 2). Как и в первом способе, проводим в окружности 2 перпендикулярных диаметра. Из точек пересечения диаметров с окружностью строим дуги с радиусом R, равным радиусу окружности (Шаг 1). Точки пересечения дуг EG и FH соединяем соответственно линиями

(Шаг 2). Точки пересечения этих линий с окружностью и являются вершинами квадрата.

Способ 3. Постройте отрезок AB, равный будущей стороне квадрата a. Постройте 2 окружности, с центрами в точках A и B и радиусом AB. Проведите прямую GH через точки пересечения окружностей. Постройте окружность, проходящую через концы отрезка и имеющую d=AB, и вторую, также проходящую через точки A и B, но с центром в точке F пересечения первой окружности с прямой GH. Соедините точки A, B, D, C. Четырехугольник ABDC — квадрат.

Построение правильного пятиугольника

Способ 1. Строим окружность произвольного радиуса R и проводим два взаимно перпендикулярных диаметра АВ и СD. Делим пополам радиус АО точкой Е. Из Е радиусом ЕС проводим дугу CF, пересекая ею диаметр АВ в точке F. Из С радиусом CF проводим дугу FG, пересекая ею данную окружность в точке G; CG (равная CF) есть одна сторона искомой фигуры. Проводим тем же радиусом дугу из точки G как из центра, получаем ещё одну вершину Н искомой фигуры и т. д. Аналогично находим вершины K и L. CGHKL — правильный пятиугольник.

Способ 2.Чтобы построить правильный пятиугольник возьмем окружность произвольного радиуса с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Отметим середину радиуса и проведем окружность, проходящую через точку O, с центром в полученной точке.

Проведем отрезок из центра маленькой окружности к точке пересечения большой окружности и ее радиуса. Построим окружность с центром в этой же точке так, чтобы она соприкасалась с маленькой окружностью.

Из точек пересечения большой и полученной окружностей проведем окружности как показано на рисунке. Для получения пятиугольника нужно соединить точки через одну.

Способ 3. Приближенное построение правильного пятиугольника. А.Дюрером оно проводилось при условии неизменности раствора циркуля, что повышает точность построения. Способ построения описан Дюрером так: «»Однако пятиугольник, построенный неизменным раствором циркуля, делай так. Проведи две окружности так, чтобы каждая из них проходила через центр другой. Два центра соедини прямой линией. Это и будет стороной пятиугольника. Точки пересечения окружностей обозначь сверху С, снизу D и проведи прямую линию CD. После этого возьми циркуль с неизменным раствором и, установив одну его ножку в точку D, другой проведи через оба центра А и В дугу до пересечения её с обеими окружностями. Точки пересечения обозначь через E и F, а точку пересечения с прямой CD обозначь буквой G. Теперь проведи прямую линию через Е и G до пересечения с линией окружности. Эту точку обозначь Н. Затем проведи другую линию через F и G до пересечения с линией окружности и поставь здесь J. Соединив J,A и H,B прямыми, получим три стороны пятиугольника. Дав возможность двум сторонам такой длины достигнуть совпадения в точке K из точек J и H, получим некоторый пятиугольник».

Способ 4. Пусть AB — заданная сторона пятиугольника — равна a. Восстановим из B перпендикуляр к AB и отложим на нем отрезок BC=a/2. Точку C соединим с точкой A. На прямой AC отложим отрезок DC=BC=a/2; затем на продолжении AB отложим AE=AD. Тогда BE равняется диагонали пятиугольника. Для построения вершин описываем из центров A и B дуги радиусами AB и BE, и в их пересечении находим вершины F, G, H.

Построение правильного шестиугольника

Построим окружность с центром в точке О. Проведем диаметр окружности. Проведем окружность того же радиуса с центром в точке пересечения диаметра с окружностью.

Проведем прямые через центр начальной окружности и точки пересечения полученной дуги с этой окружностью и соединим точки пересечения всех прямых с исходной окружностью.

Получаем правильный шестиугольник.

Способ 2. Построим окружность с центром O. Далее построим некоторую точку, принадлежащую окружности. Из данной точки на окружность раствором циркуля, равным R, откладываем последовательно отрезки (их 6). Полученные точки соединяем.

Построение правильного семиугольника

Чтобы начать построение, начертите произвольную окружность и обозначьте ее центр буквой О. Затем проведите радиус этой окружности в любом направлении. Точку пересечения радиуса с окружностью обозначьте буквой А. После этого переставьте циркуль в точку А и проведите окружность или дугу того же радиуса, что и у исходной окружности (ОА). Данная дуга пересечет исходную окружность в двух точках. Обозначьте их буквами В и С. Соедините две полученные точки. При этом отрезок ВС пересечет радиус ОА. Точку их пересечения обозначьте буквой D. Образовавшиеся при этом отрезки ВD и DC будут равны между собой и каждый из них будет приблизительно равен стороне правильного семиугольника, который можно вписать в исходную окружность. Отмерьте циркулем расстояние ВD (или DC) и, начиная с любой точки на окружности, отложите это расстояние шесть раз. Затем соедините все семь точек. Так вы получите семиугольник, который с небольшой погрешностью можно назвать правильным. Все его стороны и углы будут приблизительно равны.