Построить прямоугольник в окружности

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.

Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.

Видео:Прямоугольник в окружностиСкачать

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

• 1. Стороны прямоугольника являются его высотами.
• 2. Все углы прямоугольника прямые.
• 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
• 4. Диагонали прямоугольника равны.
• 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Видео:Как построить квадрат, два способаСкачать

Диагональ прямоугольника

Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

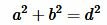(1)

Из равенства (1) найдем d:

.

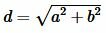(2)

Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:

Ответ:

Видео:Прямоугольник и окружностьСкачать

Окружность, описанная около прямоугольника

Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Видео:Построить описанную окружность (Задача 1)Скачать

Формула радиуса окружности описанной около прямоугольника

Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.

Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть

Подставляя (3) в (2), получим:

Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:

Ответ:

Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Периметр прямоугольника

Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Периметр прямоугольника вычисляется формулой:

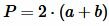(5)

где ( small a ) и ( small b ) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:

Ответ:

Видео:№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ ( small d ) и периметр ( small P ) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие ( small frac P2>d ) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

(6)

(7)

Из формулы (7) найдем ( small b ) и подставим в (6):

(8)

(9)

Упростив (4), получим квадратное уравнение относительно неизвестной ( small a ):

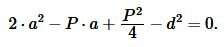(10)

Вычислим дискриминант квадратного уравнения (10):

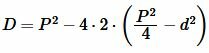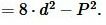(11)

Сторона прямоугольника вычисляется из следующих формул:

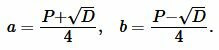(12)

После вычисления ( small a ), сторона ( small b ) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант ( small D ) из формулы (11). Для этого подставим , в (11):

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону ( small b ) из формулы (8). Подставляя значения и в формулу, получим:

Ответ: ,

Видео:Как вписать квадрат в окружностьСкачать

Признаки прямоугольника

Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.

Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.

Видео:Строим прямой уголСкачать

ИЗОБРАЖЕНИЕ ВПИСАННЫХ И ОПИСАННЫХ ОКОЛО ОКРУЖНОСТИ МНОГОУГОЛЬНИКОВ

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

ИЗОБРАЖЕНИЕ ВПИСАННЫХ И ОПИСАННЫХ ОКОЛО ОКРУЖНОСТИ МНОГОУГОЛЬНИКОВ

Задание: Дано изображение АВС произвольного треугольника А ₁ В ₁ С ₁ , вписанного в окружность. Построить изображение высоты треугольника и биссектрисы, проведенных из вершины В ₁ .

K ₁ L ₁ A ₁ C ₁ , OK ₁ L ₁ .

Соответственные построения проводим на изображении АВС треугольника А ₁ В ₁ С ₁ , вписанного в окружность.

Задание: построить изображение касательной к окружности в точке А.

Строим эллипс с центром в точке О.

Проводим диаметр АВ и сопряженный ему диаметр DC .

Проводим АК DC

АК – искомая касательная.

Задание: построить изображение прямоугольного треугольника вписанного в окружность.

чертеж — оригинал изображение

В прямоугольном треугольнике центром описанной окружности является середина гипотенузы.

Задание: построить изображение равнобедренного треугольника.

чертеж — оригинал изображение

Для построения изображения равнобедренного треугольника достаточно построить два сопряженных диаметра. В случае остроугольного и тупоугольного равнобедренных треугольников строят хорду параллельную одному из сопряженных диаметров, которая послужит основанием треугольника. В случае, когда речь идет о прямоугольном равнобедренном треугольнике, один из сопряженных диаметров послужит основанием искомого треугольника.

Вершина искомого треугольника будет лежать на конце другого диаметра.

Задание: построить изображение правильного треугольника вписанного в окружность.

чертеж — оригинал изображение

Задание: построить изображение прямоугольника вписанного в окружность.

чертеж — оригинал изображение

Задание: построить изображение вписанной в окружность равнобокой трапеции.

чертеж – оригинал изображение

Задание: построить изображение квадрата вписанного в окружность.

чертеж – оригинал изображение

Задание: построить изображение правильного шестиугольника вписанного в окружность

Проведем ω(О; ОА ₁ ), (А ₁ А ₄ ) ( MN ), О = (А ₁ А ₄ ) ( MN ), ОА ₁ = R .

1.Строим эллипс (с центром О ).

2. Строим произвольный диаметр А′ ₁ А′ ₄ и сопряженный ему диаметр MN .

Задание: построить изображение описанного около окружности прямоугольного треугольника.

чертеж — оригинал изображение

Для построения изображения описанного около окружности прямоугольного треугольника используют тот факт, что его катеты это касательные к окружности в концах двух его сопряженных диаметров.

чертеж — оригинал изображение

Строим эллипс с центром в точке О и два сопряженных диаметра MN и KL .

Из точки В , лежащей на продолжении диаметра KL , проводим две касательные ( Р и Q – точки касания) до пересечения с прямой АС ( АС MN ).

Треугольник АВС является искомым равнобедренным треугольником.

Задание: построить изображение описанного около окружности равностороннего треугольника.

чертеж — оригинал изображение

Построение равностороннего треугольника аналогично построению равнобедренного треугольника. За исключением того, что здесь точку В выбирают не произвольно, а так, чтобы OL = LB .

Задание: построить изображение описанного около окружности квадрата.

чертеж — оригинал изображение

Стороны квадрата лежат на касательных к окружности, проходящих в концах сопряженных диаметром MN и KL . Точки касания делят стороны описанного квадрата пополам.

Задание: построить изображение ромба описанного около окружности.

чертеж — оригинал изображение

Диагоналям ромба АС и BD принадлежат сопряженные диаметры эллипса KL и MN соответственно. Одну из вершин ромба выбираем произвольно, например, вершину С . Из этой вершины проводим касательные отрезки. Например, отрезок CD касается эллипса в точке Р .

Замечание: точка Р не должна делить отрезок CD пополам, иначе, получим изображение описанного квадрата.

Задание: построить изображение описанной около окружности равнобокой трапеции.

чертеж — оригинал изображение

При построении изображения описанной около окружности равнобокой трапеции стоит учитывать, что диаметр K ₁ L ₁ перпендикулярен основаниям В ₁ С ₁ и А ₁ D ₁ и делит их пополам.

Строим касательные к эллипсу, проходящие через точки К и L , параллельные диаметру MN ( MN и KL сопряженные диаметры). Откладываем два равных отрезка КВ и КС , так чтобы КС был меньше ON . Через точки В и С проводим касательные к эллипсу. Точки пересечения этих касательных с касательной, проведенной в точке L , дают вершины A и D .

Второй способ:

Строим вписанную в окружность трапеции (см.выше). Затем проводим касательные к эллипсу параллельные сторонам трапеции. Точки пересечения касательных – вершимы искомой описанной равнобокой трапеции.

Задание: построить изображение описанного около окружности шестиугольника.

чертеж — оригинал изображение

Видео:№701. Начертите три треугольника: остроугольный, прямоугольный и тупоугольный. В каждыйСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Курс добавлен 12.01.2022
• Сейчас обучается 931 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Курс добавлен 12.01.2022
• Сейчас обучается 703 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Курс добавлен 12.01.2022
• Сейчас обучается 335 человек из 72 регионов

Ищем педагогов в команду «Инфоурок»

Практическая значимость исследования состоит в разработке научно обоснованной системы упражнений и конкретных методических рекомендаций по развитию графической культуры и формированию общепрактических навыков и умений у учащихся 10 -11 классов на уроках геометрии, элективных занятиях, лекциях и семинарах. Результаты исследования могут быть использованы учителями школ и методистами.

• Голованова Елена ПавловнаНаписать 6193 06.05.2018

Номер материала: ДБ-1556032

04.05.2018 1165

04.05.2018 924

04.05.2018 784

04.05.2018 273

04.05.2018 243

04.05.2018 160

04.05.2018 241

04.05.2018 721

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России ежегодно будут обучать плаванию не менее 500 тыс. детей

Время чтения: 2 минуты

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Проходной балл ЕГЭ для поступления на бюджет снизился впервые за 10 лет

Время чтения: 3 минуты

В Госдуме обсудят введение обязательных тестов на наркотики в школах

Время чтения: 1 минута

Стоимость обучения на первом курсе в вузах РФ за год выросла на 10%

Время чтения: 3 минуты

Ретроспектива культовой сказки «Вечера на Хуторе близ Диканьки»

Время чтения: 5 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Построение равностронего треугольника.Скачать

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

1. Приемы построения геометрических объектов на чертежах;

2. Способы редактирования чертежей;

3. Автоматизированное нанесение размеров на чертежах;

4. Вывод чертежей на печать.

ПРИЕМЫ ПОСТРОЕНИЯ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ

К основным геометрическим объектам в системе КОМПАС относятся:

Кнопки для вызова команд вычерчивания перечисленных геометрических объектов расположены на панели Геометрия (рис.21).

Рис.21 Панель Геометрия

ВЫЧЕРЧИВАНИЕ ВСПОМОГАТЕЛЬНЫХ ПРЯМЫХ

Расширенная панель Вспомогательные прямые на инструментальной панели Геометрия позволяет построить различным образом расположенные вспомогательные прямые, используемые для предварительных построений (рис. 22).

Рис.22 Расширенная панель Вспомогательная прямая

Черный треугольник в углу кнопки показывает, что кнопка разворачивается, т.е. имеется расширенная панель. Возможно построение:

1. Вспомогательной прямой в указанной точке по углу ее наклона;

2. Горизонтальной вспомогательной прямой в указанной точке;

3. Вертикальной прямой;

4. Вспомогательных прямых, параллельных указанной линии;

5. Вспомогательной прямой, перпендикулярной к указанной линии;

6. Различных вспомогательных касательных линий;

7. Биссектрисы угла.

Для переключения между кнопками расширенной панели следует несколько секунд, не отпуская, задержать курсор на одной из кнопок.

Рис.23 Построение вспомогательных параллельных прямых

Для построения параллельных вспомогательных прямых (используется кнопка ) следует курсором-ловушкой, появившемся на экране после включения кнопки Параллельная прямая, указать базовый объект, параллельно которому будут строиться вспомогательные прямые. Чтобы задать расстояние от базового объекта до параллельной прямой, введите нужное значение в поле Расстояние на Панели свойств (рис.23) или укажите точку, через которую должна пройти прямая. Если требуется показать точки пересечения вспомогательной прямой со всеми графическими объектами, используется переключатель Точки пересечения , расположенный на Панели свойств.

По умолчанию система предлагает фантомы двух прямых, расположенных на заданном расстоянии по обе стороны от базового объекта.

Управление количеством прямых производится с помощью переключателя Количество прямых на Панели свойств.

Вы можете зафиксировать одну из них или обе, щелкая мышью на нужном фантоме либо нажимая кнопку Создать объект на Панели специального управления.

Панель специального управления (рис.24) – появляется только после вызова какой- либо команды и позволяет редактировать процесс выполнения этой команды:

Рис.24 Панель специального управления

Если была допущена ошибка в построениях, то кнопка Отменить/Повторить позволяет отменить (вернуть) предыдущее действие пользователя, если это возможно.

Для выхода из команды нажмите кнопку Прервать команду на Панели специального управления или клавишу .

ВЫЧЕРЧИВАНИЕ ОТРЕЗКА

Чтобы построить отрезок, следует нажать на кнопку Отрезок панели Геометрия (рис.20). На Панели свойств внизу экрана можно задать длину отрезка, угол его наклона и стиль.

СТИЛИ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ

Геометрические объекты можно вычерчивать различными по стилю линиями – тонкими, сплошными основными, штриховыми и т.д. Стиль выбирается из списка, расположенного на Панели свойств внизу экрана (рис.25).

Рис.25 Построение отрезка

ТОЧНОЕ ЧЕРЧЕНИЕ – ПРИВЯЗКИ

В процессе работы над чертежами часто возникает необходимость точно установить курсор в различные характерные точки элементов, иными словами, выполнить привязку к точкам или объектам. Для вызова этого диалога служит кнопка Установка глобальных привязок (рис.26 и 27), возможно также отключение действия всех глобальных привязок, а затем включение их вновь в прежнем составе, для чего служит кнопкой Запретить/разрешить действие глобальных привязок на Панели текущего состояния.

Рис.26 Установка и отключение привязок

Рис.27 Установка глобальных привязок

ГЕОМЕТРИЧЕСКИЙ КАЛЬКУЛЯТОР

Очень удобным и точным вспомогательным средством отрисовки различных объектов чертежа является инструмент, который в КОМПАС 5 называется геометрическим калькулятором . Он позволяет «снимать» непосредственно с элементов чертежа различные координатные, линейные и угловые параметры. Эти данные используются затем при построении или редактировании других объектов.

Калькулятор запускается щелчком правой кнопки мыши. Перечень возможных вариантов для снятия значений варьируется в зависимости от поля строки параметров, из которого был вызван калькулятор. Например, если геометрический калькулятор запущен из поля длины отрезка, то будут предложены команды для снятия линейных параметров (длины кривой, расстояния между двумя точками, радиуса окружности и т. п.) (рис.26), а для поля угла наклона отрезка появится меню снятия угловых величин (рис.27).

Рис.26 Геометрический калькулятор для измерения расстояний

Рис.27 Геометрический калькулятор для снятия значений угловых величин

ВЫДЕЛЕНИЕ, ПЕРЕМЕЩЕНИЕ, ИЗМЕНЕНИЕ И УДАЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ

1 ) Для того чтобы выделить объект на чертеже, например, отрезок, следует:

· Отключить кнопку стоп на Панели специального управления;

· Щелкнуть по объекту – он выделится зеленым цветом.

2) Для того чтобы переместить объект , следует:

· Зацепить его курсором и, не отпуская, переместить в нужное место.

3) Для того чтобы удалить объект , следует:

1. Выделить объект;

2. Нажать на клавишу Delete на клавиатуре.

Для удаления различных объектов служит пункт меню Редактор — Удалить- ….. (рис.28) и кнопки Усечь кривую и Усечь кривую между двумя точками (рис.29) на инструментальная панель Редактирование (рис.15).

4) Для того чтобы изменить объект, следует:

· Два раза щелкнуть по объекту;

· Изменить параметры (длину, угол, стиль);

· Щелкнуть по кнопке Создать объект.

Рис.28 Удаление объектов

Рис.29 Расширенная панель Усечь кривую

ЛИНЕЙНЫЕ РАЗМЕРЫ

Для нанесения линейных размеров на инструментальной панели Размеры используются кнопки Линейный размер и Авторазмер (рис.30)

Рис.30 Панель Размеры

При использовании кнопки Линейный размер система автоматически проставит размер, равный расстоянию, между двумя указанными курсором точками (т1 и т2) привязки размера — точками выхода выносных линий. Третья указанная точка (т3) определяет положение размерной линии. Элементы управления создаваемым размером располагаются в панели свойств внизу экрана (рис.31).

Рис.31 Вкладка с элементами управления создаваемым размером

Линейные размеры могут располагаться параллельно линии, горизонтально или вертикально.

Вкладка Параметры служит для управления создаваемым размером (рис.32) и содержит следующие кнопки:

Рис. 32 Вкладка Параметры

	1) Переключатели, управляющие отрисовкой первой и второй выносными линиями размера.
	2) Список, позволяющий выбрать вид первой и второй стрелки размера;
	3) Список, позволяющий указать нужный способ размещения размерной надписи.

Диалог ввода размерной надписи позволяет задать нужное значение размера и настроить его оформление. Щелчок мыши по этой кнопке открывает окно, изображенное на рис.33.

Рис.33 Задание размерной надписи

Кнопка Авторазмер позволяет построить размер, тип которого автоматически определяется системой в зависимости от того, какие объекты указаны для простановки размера.

Порядок и способы указания геометрических объектов зависят от того, какой именно размер требуется проставить:

· Линейный с обрывом;

· Линейный от отрезка до точки.

Для выхода из команды простановки размера нажмите кнопку Прервать команду на Панели специального управления или клавишу .

ПОСТРОЕНИЕ ОКРУЖНОСТИ

Для построения окружностей используется кнопка Построение окружности по центру и точке инструментальной панели Геометрия (рис.20).

Для построения окружности укажите на чертеже центр окружности или введите его координаты с клавиатуры. Затем укажите точку, лежащую на окружности или введите в строке Свойств (рис.34) величину радиуса.

Рис.34 Панель свойств окружностей

Группа переключателей Оси на Панели свойств позволяет вычерчивать окружности с осями симметрии или без осей.

Кнопка Запомнить состояние позволяет запомнить параметры, которые были заданы при вводе объекта, для того, чтобы использовать их при создании следующих объектов.

Для того чтобы вычертить несколько окружностей с одинаковым радиусом, нужно ввести значение радиуса, и до фиксации этой окружности на чертеже нажать кнопку Запомнить состояние, заданный радиус будет автоматически предлагаться в строке параметров объектов при вводе следующей окружности.

Чтобы построить несколько концентрических окружностей из одного центра, укажите точку центра и нажмите кнопку Запомнить состояние. Затем последовательно создавайте окружности, указывая лежащие на них точки или вводя значение радиусов с клавиатуры. За один вызов команды можно построить произвольное число окружностей.

Для выхода из команды нажмите кнопку Прервать команду на Панели специального управления или клавишу .

ДИАМЕТРАЛЬНЫЙ РАЗМЕР

Для проставления размеров окружностей используется кнопка Диаметральный размер, расположенная на Инструментальной панели Размеры (рис.30).

Рис.35 Вкладка с элементами управления диаметральным размером

Переключатель позволяет указать тип размерной линии диаметрального размера: полная или с обрывом. Для выбора нужного варианта нажмите нужную кнопку в группе Тип на вкладке Размер Панели свойств (рис.35).

Кнопка служит для ввода размерной надписи, ее окно аналогично окну линейного размера (см. рис.33).

Вкладка Параметры служит для управления создаваемым размером и содержит кнопки, изображенные на рис.32.

ДЕЛЕНИЕ ЛИНИИ НА РАВНЫЕ ЧАСТИ

Кнопка Точки по кривой (рис.36), расположенная на расширенной панели Точка, позволяет построить нескольких точек, равномерно расположенных на какой-либо кривой.

Количество участков, на которые проставленные точки должны разбить кривую, указываются в поле Количество участков (рис.37) на Панели свойств. Затем указывается курсором кривая для простановки точек.

Рис.36 Расширенная панель Точка

Если кривая не замкнута, точки будут построены сразу после ее указания. Первая точка будет совпадать с начальной точкой кривой, последняя — с конечной.

Рис. 37 Панель свойств

Если кривая замкнута, то после ее указания требуется задать положение первой точки на ней (определить точку т1).

ПОСТРОЕНИЕ ДУГИ

Для построения дуги используется кнопка Дуга, расположенная на инструментальной панели Геометрия (рис.20).

Рис.38 Панель свойств дуги

На Панели свойств изображаемой дуги (рис.38) расположены окно для ввода радиуса дуги с клавиатуры, переключатель, позволяющий выбрать направление построения дуги: по часовой стрелке или против часовой стрелки, окно для выбора стиля линии.

РАДИАЛЬНЫЙ РАЗМЕР

Для нанесения размеров дуг используется кнопка Радиальный размер, расположенная на Инструментальной панели Размеры (рис.30). На панели управления (рис.39) можно выбрать Тип размерной линии радиального размера: от центра или не от центра, ввести текст размерной надписи.

Вкладка Параметры служит для управления создаваемым размером и содержит кнопки, изображенные на рис.32.

Рис.39 Вкладка управления радиальным размером

ПОСТРОЕНИЕ ПРЯМОУГОЛЬНИКА

Для построения прямоугольников используются кнопки Прямоугольник и Прямоугольник по центру и вершине, расположенные на расширенной панели (рис.40).

Рис.40 Расширенная панель Прямоугольник

Кнопка дает возможность построить прямоугольник двумя способами:

— задание противоположных вершин прямоугольника,

— задание вершины, высоты и ширины прямоугольника.

Если известно положение вершин прямоугольника (точки т1 и т2), следует указать их. При этом высота и ширина прямоугольника будут определены автоматически.

Если известны вершина, высота и ширина прямоугольника, задайте их любым способом и в любом порядке. Например, вы можете указать курсором положение вершины, ввести высоту в поле Панели свойств (рис.42) и задать курсором ширину прямоугольника. При этом координаты вершины, противолежащей указанной, будут определены автоматически.

Рис. 42 Панель свойств выполнения команды Прямоугольник

Группа переключателей Оси на Панели свойств управляет отрисовкой осей симметрии прямоугольника.

Для выхода из команды нажмите кнопку Прервать команду на Панели специального управления или клавишу .

Прямоугольник, построенный в графическом документе, — это единый объект, а не набор отдельных отрезков. Он будет выделяться, редактироваться и удаляться целиком.

Кнопка Прямоугольник по центру и вершине позволяет построить прямоугольник с заданными центром и вершиной. Курсором или вводом координат с клавиатуры указывается центр прямоугольника. Затем можно указать одну из вершин прямоугольника или ввести значения высоты и ширины прямоугольника в одноименные окна на панели свойств (рис.43).

Рис. 43 Панель свойств выполнения команды Прямоугольник по центру и вершине

ПОСТРОЕНИЕ МНОГОУГОЛЬНИКА

Кнопка Многоугольник позволяет построить правильный многоугольник. Количество вершин можно задать с клавиатуры или выбрать из списка на Панели свойств (рис.44).

Переключатели Способ построения позволяют строить многоугольник по вписанной или по описанной окружности.

Рис. 44 Панель свойств выполнения команды Многоугольник

Точку центра базовой окружности можно указать курсором или ввести ее координаты с клавиатуры в окна Центр на панели свойств (рис.41), затем задается величина радиуса описанной окружности.

Многоугольник – это единый объект, а не набор отдельных отрезков. Он будет выделяться, редактироваться и удаляться целиком.

ФАСКИ

Кнопка Фаска позволяет построить отрезок, соединяющий две пересекающиеся кривые, т.е. «притупить» угол.

Рис.45 Панель свойств команды Фаска

Переключатель позволяет выбрать способ построения фаски: по двум длинам или по длине и углу.

СКРУГЛЕНИЕ

Кнопка Скругление позволяет построить скругление дугой окружности между двумя пересекающимися объектами. Радиус скругления задается на панели свойств (рис.46).

Рис.46 Панель свойств команды Скругление

ШТРИХОВКА

Если необходимо заштриховать одну или несколько областей в текущем виде чертежа или во фрагменте, то для вызова команды используется кнопка Штриховка на инструментальной панели Геометрия.

Штриховка строится автоматически, если выполнены следующие условия:

1. Контур (граница) штриховки вычерчен основной линией или линией для обрыва;

2. Контур замкнут.

Укажите точку внутри области, которую нужно заштриховать. Система автоматически определит ближайшие возможные границы, внутри которых указана точка.

Кнопки Панели специального управления (рис.47) предоставляют дополнительные возможности создания границ штриховки. Кнопка Ручное формирование границ позволяет перейти к созданию временной ломаной линии, а кнопка Обход границы по стрелке — к формированию контура, образованного пересекающимися объектами.

Для настройки параметров штриховки служат элементы Панели свойств (рис.47).

Из списка Стиль можно выбрать стиль штриховки (металл, камень, дерево и т.п.).

Список Цвет позволяет выбрать цвет штриховки. Щелчок на строке Другие цвета выводит на экран расширенный диалог выбора цвета.

В полях Шаг и Угол можно ввести или выбрать из списка шаг и угол наклона штриховки.

Рис. 47 Панель свойств команды Штриховка

Чтобы зафиксировать полученную штриховку и перейти к построению следующей, нажмите кнопку Создать объект на Панели специального управления.

ВЫВОД ЧЕРТЕЖА НА ПЕЧАТЬ

После того как чертеж создан, и нужно получить его бумажную копию, следует перейти в режим предварительного просмотра для печати. Это особый режим КОМПАСа, в котором можно видеть реалистичное изображение документа, разместить документ на поле вывода, выбрать только какую-либо часть для вывода, изменить масштаб вывода и так далее.

В режиме предварительного просмотра документы недоступны для редактирования.

Для входа в режим используется команда Файл — Предварительный просмотр или одноименная кнопка на панели Стандартная в верхней части экрана (рис.48).

Рис.48 Панель Стандартная

Текущий документ будет загружен в режим предварительного просмотра, который позволяет вывести на печать содержимое окна просмотра. После вызова команды на экране появится диалог, в котором можно задать параметры печати.

Режим предварительного просмотра имеет собственное Главное меню, Панель управления (рис.49) и Панель свойств (рис.50).

Рис.49 Панель управления в режиме предварительного просмотра

Рис.50 Панель свойств в режиме предварительного просмотра

В режиме предварительного просмотра на экране показывается условное поле вывода (один или несколько листов бумаги). На нем реалистично отображается документ (или несколько документов). По умолчанию поле вывода отображается на экране в таком масштабе, чтобы оно было видно полностью.

Если большой документ выводится на малогабаритное печатающее устройство (например, на принтер), выполняется автоматическая разбивка на листы соответствующего формата. При этом поле вывода в режиме просмотра разделяется пунктирными линиями на части, соответствующие установленному в данный момент формату бумаги и ее ориентации.

Чтобы более рационально использовать бумагу, можно повернуть чертеж с помощью кнопок Повернуть по часовой стрелке и Повернуть против часовой стрелки.

Если требуется уместить большой чертеж на меньшем формате, например, чертеж формата А3 на листе формата А4, то для такого размещения документов используется команда Сервис — Подогнать масштаб. (рис.51).

Рис.51 Подгонка масштаба документа

Можно напечатать не весь текущий документ целиком, а только его часть — область, ограниченную прямоугольником произвольных размеров.

Для этого используется переключатель Указать часть на Панели свойств.

На экране появится диалог, в котором показан текущий документ и рамка, ограничивающая печатаемую часть. По умолчанию размеры рамки соответствуют габаритам изображения.

Чтобы изменить размеры рамки, вводятся нужные значения в поля группы Отступ в левой части диалога. Можно также переместить стороны или углы рамки мышью. После этого на поле вывода будет отображаться не весь документ, а только указанная часть.

Можно управлять способом печати текущего документа с помощью переключателей группы Способ вывода (рис.50) на Панели свойств. Активизация переключателя Вывести часть текущего документа отображает на поле вывода область документа, ограниченную рамкой, активизация переключателя Вывести текущий документ полностью — весь документ целиком.

Часть документа можно переместить, повернуть на поле вывода или промасштабировать так же, как и целый документ.

После того, как документ размещен наилучшим образом, необходимо вызвать команду Файл — Печать для начала вывода документа на бумагу или нажать кнопку Печать на Панели управления (рис.49).

Чтобы закончить работу в режиме предварительного просмотра, используется кнопка Закончить просмотр на Панели управления или соответствующая команда из меню Файл.

Система вернется в обычный режим редактирования документов.

ПРИМЕР ЧЕРТЕЖА

Рассмотрим последовательность действий при построении чертежа крышки, представленной на рис.52.

Рис. 52 Чертеж крышки

1. Создать формат А4, заполнить основную надпись.

2. Включить Привязки — Середина, Пересечение, Выравнивание, Точка на кривой (см. рис.27).

3. Построить правильный квадрат с описанной окружностью радиусом 50 (рис.53), используя кнопку Многоугольник (рис.44).

4. Из середин сторон квадрата, как из центров, построить дуги радиусом R 20.

5. Построить вспомогательные линии через центры дуг и центр квадрата.

6. Прочертить осевые линии для дуг (рис.54) поверх вспомогательных линий, используя привязку Точка на кривой. Стереть вспомогательные линии.

7. Стереть части сторон квадрата между концами дуг, используя кнопку Усечь кривую (рис.29).

8. Построить окружность радиусом 30 мм осевой линией (рис.55), разделить ее на шесть частей. Из полученных точек как из центров построить шесть окружностей R 5.

9. Прочертить осевые линии для окружностей, используя вспомогательные линии и привязку Точка на кривой.

🔍 Видео

Прямоугольник и окружностьСкачать

Деление окружности на 3; 6; 12 равных частейСкачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Построение пятиугольника циркулемСкачать

ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

4K Как построить правильный пятиугольник, how to draw a regular pentagonСкачать

Задачи на построение с помощью циркуля и линейки - 7 класс геометрияСкачать

Как построить шестиугольник вписанный в окружностьСкачать

Вписанная и описанная окружность - от bezbotvyСкачать