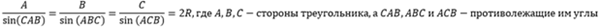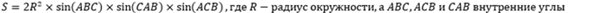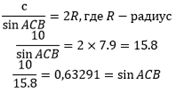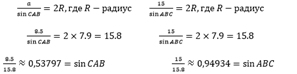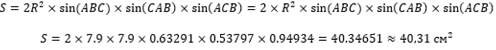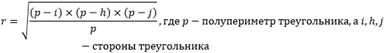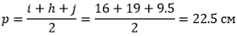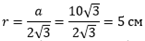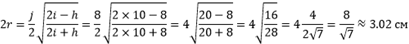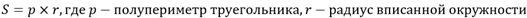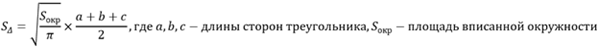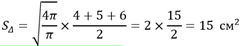Построить изображение прямоугольного треугольника вписанного в окружность

Видео:Построить описанную окружность (Задача 1)Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Как построить шестиугольник вписанный в окружностьСкачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Построение треугольника в трёх проекцияхСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Изображение в изометрической проекции окружностей, вписанных в кубСкачать

ИЗОБРАЖЕНИЕ ВПИСАННЫХ И ОПИСАННЫХ ОКОЛО ОК-РУЖНОСТИ МНОГОУГОЛЬНИКОВ

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Центр окружности описанной вокруг треугольникаСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

ИЗОБРАЖЕНИЕ ВПИСАННЫХ И ОПИСАННЫХ ОКОЛО ОКРУЖНОСТИ МНОГОУГОЛЬНИКОВ

Задание: Дано изображение АВС произвольного треугольника А ₁ В ₁ С ₁ , вписанного в окружность. Построить изображение высоты треугольника и биссектрисы, проведенных из вершины В ₁ .

K ₁ L ₁ A ₁ C ₁ , OK ₁ L ₁ .

Соответственные построения проводим на изображении АВС треугольника А ₁ В ₁ С ₁ , вписанного в окружность.

Задание: построить изображение касательной к окружности в точке А.

Строим эллипс с центром в точке О.

Проводим диаметр АВ и сопряженный ему диаметр DC .

Проводим АК DC

АК – искомая касательная.

Задание: построить изображение прямоугольного треугольника вписанного в окружность.

чертеж — оригинал изображение

В прямоугольном треугольнике центром описанной окружности является середина гипотенузы.

Задание: построить изображение равнобедренного треугольника.

чертеж — оригинал изображение

Для построения изображения равнобедренного треугольника достаточно построить два сопряженных диаметра. В случае остроугольного и тупоугольного равнобедренных треугольников строят хорду параллельную одному из сопряженных диаметров, которая послужит основанием треугольника. В случае, когда речь идет о прямоугольном равнобедренном треугольнике, один из сопряженных диаметров послужит основанием искомого треугольника.

Вершина искомого треугольника будет лежать на конце другого диаметра.

Задание: построить изображение правильного треугольника вписанного в окружность.

чертеж — оригинал изображение

Задание: построить изображение прямоугольника вписанного в окружность.

чертеж — оригинал изображение

Задание: построить изображение вписанной в окружность равнобокой трапеции.

чертеж – оригинал изображение

Задание: построить изображение квадрата вписанного в окружность.

чертеж – оригинал изображение

Задание: построить изображение правильного шестиугольника вписанного в окружность

Проведем ω(О; ОА ₁ ), (А ₁ А ₄ ) ( MN ), О = (А ₁ А ₄ ) ( MN ), ОА ₁ = R .

1.Строим эллипс (с центром О ).

2. Строим произвольный диаметр А′ ₁ А′ ₄ и сопряженный ему диаметр MN .

Задание: построить изображение описанного около окружности прямоугольного треугольника.

чертеж — оригинал изображение

Для построения изображения описанного около окружности прямоугольного треугольника используют тот факт, что его катеты это касательные к окружности в концах двух его сопряженных диаметров.

чертеж — оригинал изображение

Строим эллипс с центром в точке О и два сопряженных диаметра MN и KL .

Из точки В , лежащей на продолжении диаметра KL , проводим две касательные ( Р и Q – точки касания) до пересечения с прямой АС ( АС MN ).

Треугольник АВС является искомым равнобедренным треугольником.

Задание: построить изображение описанного около окружности равностороннего треугольника.

чертеж — оригинал изображение

Построение равностороннего треугольника аналогично построению равнобедренного треугольника. За исключением того, что здесь точку В выбирают не произвольно, а так, чтобы OL = LB .

Задание: построить изображение описанного около окружности квадрата.

чертеж — оригинал изображение

Стороны квадрата лежат на касательных к окружности, проходящих в концах сопряженных диаметром MN и KL . Точки касания делят стороны описанного квадрата пополам.

Задание: построить изображение ромба описанного около окружности.

чертеж — оригинал изображение

Диагоналям ромба АС и BD принадлежат сопряженные диаметры эллипса KL и MN соответственно. Одну из вершин ромба выбираем произвольно, например, вершину С . Из этой вершины проводим касательные отрезки. Например, отрезок CD касается эллипса в точке Р .

Замечание: точка Р не должна делить отрезок CD пополам, иначе, получим изображение описанного квадрата.

Задание: построить изображение описанной около окружности равнобокой трапеции.

чертеж — оригинал изображение

При построении изображения описанной около окружности равнобокой трапеции стоит учитывать, что диаметр K ₁ L ₁ перпендикулярен основаниям В ₁ С ₁ и А ₁ D ₁ и делит их пополам.

Строим касательные к эллипсу, проходящие через точки К и L , параллельные диаметру MN ( MN и KL сопряженные диаметры). Откладываем два равных отрезка КВ и КС , так чтобы КС был меньше ON . Через точки В и С проводим касательные к эллипсу. Точки пересечения этих касательных с касательной, проведенной в точке L , дают вершины A и D .

Второй способ:

Строим вписанную в окружность трапеции (см.выше). Затем проводим касательные к эллипсу параллельные сторонам трапеции. Точки пересечения касательных – вершимы искомой описанной равнобокой трапеции.

Задание: построить изображение описанного около окружности шестиугольника.

чертеж — оригинал изображение

Краткое описание документа:

Практическая значимость исследования состоит в разработке научно обоснованной системы упражнений и конкретных методических рекомендаций по развитию графической культуры и формированию общепрактических навыков и умений у учащихся 10 -11 классов на уроках геометрии, элективных занятиях, лекциях и семинарах. Результаты исследования могут быть использованы учителями школ и методистами.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 931 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 67 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 682 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 494 226 материалов в базе

Материал подходит для УМК

«Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.

88. Вписанный четырехугольник

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Дистанционные курсы для педагогов

Другие материалы

• 04.05.2018
• 2858

• 04.05.2018
• 2950

• 04.05.2018
• 1765

• 04.05.2018
• 450

• 04.05.2018
• 490

• 04.05.2018
• 311

• 04.05.2018
• 502

• 04.05.2018
• 1833

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 06.05.2018 6343 —> —> —> —>
• DOCX 731 кбайт —> —>
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Голованова Елена Павловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 3 года и 11 месяцев
• Подписчики: 4
• Всего просмотров: 121767
• Всего материалов: 90

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Крупнейшие вузы Татарстана откроют цифровые кафедры в 2022 году

Время чтения: 1 минута

В школьном курсе мировой истории планируют уделить больше внимания Азии и Африке

Время чтения: 1 минута

Минпросвещения России запускает конкурс для учителей физкультуры

Время чтения: 2 минуты

В России могут создать комиссию по поддержке одаренных детей

Время чтения: 1 минута

Орловские школы переведут на дистанционное обучение с 24 января

Время чтения: 1 минута

Санкт-Петербургский госуниверситет переходит на дистанционное обучение

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Параллельное проектирование и его свойства Изображение пространственных фигурСкачать

Формула площади и радиуса: свойства треугольника, вписанного в окружность

В современном машиностроении используется масса элементов и запчастей, которые имеют в своей структуре как внешние окружности, так и внутренние. Самым ярким примером могут служить корпус подшипника, детали моторов, узлы ступицы и многое другое. При их изготовлении применяются не только высокотехнологичные приспособления, но и знания из геометрии, в частности информация об окружностях треугольника. Более детально с подобным знаниями познакомимся ниже….

Видео:Геометрия - Построение правильного треугольникаСкачать

Какая окружность вписана, а какая описана

Прежде всего вспомним, что окружностью называется бесконечное множество точек, удаленных на одинаковом расстоянии от центра. Если внутри многоугольника допускается построить окружность, которая с каждой стороной будет иметь только одну общую точку пересечения, то она будет называться вписанной. Описанной окружностью (не круг, это разные понятия) называется такое геометрическое место точек, при котором у построенной фигуры с заданным многоугольником общими точками будут только вершины многоугольника. Ознакомимся с этими двумя понятиями на более наглядном примере (см. рис 1.).

Рисунок 1. Вписанная и описанная окружности треугольника

На изображении построены две фигуры большого и малого диаметров, центры которых находятся G и I. Окружность большего значения называется описанной окр-тью Δ ABC, а малого – наоборот, вписанной в Δ ABC.

Для того чтобы описать вокруг треугольника окр-ть, требуется провести через середину каждой стороны перпендикулярную прямую (т.е. под углом 90°) – это точка пересечения, она играет ключевую роль. Именно она будет представлять собой центр описанной окружности. Перед тем как найти окружность, ее центр в треугольнике, требуется построить для каждого угла биссектрису, после чего выделить точку пересечения прямых. Она в свою очередь будет центром вписанной окр-ти, а ее радиус при любых условиях будет перпендикулярен любой из сторон.

На вопрос:«Какое количество окружностей вписанных может быть для многоугольника с тремя углами?» ответим сразу, что в любой треугольник можно вписать окружность и притом только одну. Потому что существует только одна точка пересечения всех биссектрис и одна точка пересечения перпендикуляров, исходящих из середин сторон.

Видео:2 2 3 построение изометрии окружностиСкачать

Свойство окружности, которой принадлежат вершины треугольника

Описанная окружность, которая зависит от длин сторон при основании, имеет свои свойства. Укажем свойства описанной окружности:

1. Центр описанной окружности для прямоугольного треугольника находится на середине гипотенузы, у острого – внутри самого треугольника, а для тупоугольного – за ее пределами.
2. Диаметр любой описанной окр-сти равен половине отношения стороны и синуса угла, который принадлежит ей, в виде формулы можно представить следующим образом:
3. Зная радиус описанной окружности и значения углов, можно найти значение площади, не прибегая к использованию длин сторон, по следующей формуле:

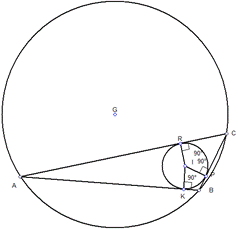
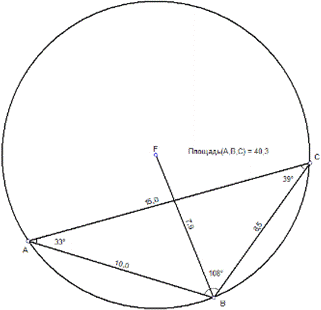
Для того чтобы более наглядно понять принцип описанной окружности, решим простую задачу. Допустим, что дан треугольник Δ ABC, стороны которого равны 10, 15 и 8,5 см. Радиус описанной окружности около треугольника (FB) составляет 7,9 см. Найти значение градусной меры каждого угла и через них площадь треугольника.

Рисунок 2. Поиск радиуса окружности через отношение сторон и синусов углов

Решение: опираясь на ранее указанную теорему синусов, найдем значение синуса каждого угла в отдельности. По условию известно, что сторона АВ равна 10 см. Вычислим значение С:

Используя значения таблицы Брадиса, узнаем, что градусная мера угла С равна 39°. Таким же методом найдем и остальные меры углов:

Откуда узнаем, что CAB = 33°, а ABC = 108°. Теперь, зная значения синусов каждого из углов и радиус, найдем площадь, подставляя найденные значения:

Ответ: площадь треугольника равна 40,31 см², а углы равны соответственно 33°, 108° и 39°.

Важно! Решая задачи подобного плана, будет нелишним всегда иметь таблицы Брадиса либо соответствующее приложение на смартфоне, так как вручную процесс может затянуться на длительное время. Также для большей экономии времени не требуется обязательно строить все три середины перпендикуляра либо три биссектрисы. Любая третья из них всегда будет пересекаться в точке пересечения первых двух. А для ортодоксального построения обычно третью дорисовывают. Может, это неправильно в вопросе алгоритма, но на ЕГЭ или других экзаменах это здорово экономит время.

Исчисление радиуса вписанной окружности

Все точки окружности одинаково удалены от ее центра на одинаковом расстоянии. Длину этого отрезка (от и до) называют радиусом. В зависимости от того, какую окр-ть мы имеем, различают два вида – внутренний и внешний. Каждый из них вычисляется по собственной формуле и имеет прямое отношение к вычислению таких параметров, как:

• площадь,
• градусная мера каждого угла,
• длины сторон и периметр.

Рисунок 3. Расположение вписанной окружности внутри треугольника

Вычислить длину расстояния от центра до точки соприкосновения с любой из сторон можно такими способами: через стороны, высоты, боковые стороны и углы (для равнобокого треугольника).

Использование полупериметра

Полупериметром называется половина суммы длин всех сторон. Такой способ считается самым популярным и универсальным, потому как независимо от того, какой тип треугольника дан по условию, он подходит для всех. Порядок вычисления имеет следующий вид:

Если дан «правильный»

Одним из малых преимуществ «идеального» треугольника является то, что вписанная и описанная окружности имеют центр в одной точке. Это удобно при построении фигур. Однако в 80% случаев ответ получается «некрасивым». Тут имеется ввиду, что очень редко радиус вписанной окр-ти будет целым натуральным числом, скорее наоборот. Для упрощенного исчисления используется формула радиуса вписанной окружности в треугольник:

Если боковины одинаковой длины

Одним из подтипов задач на гос. экзаменах будет нахождение радиуса вписанной окружности треугольника, две стороны которого равны между собой, а третья нет. В таком случае рекомендуем использовать этот алгоритм, который даст ощутимую экономию времени на поиск диаметра вписанной окр-ти. Радиус вписанной окружности в треугольник с равными «боковыми» вычисляется по формуле:

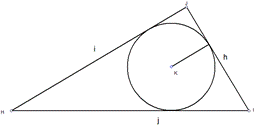
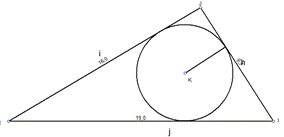
Более наглядное применение указанных формул продемонстрируем на следующей задаче. Пускай имеем треугольник (Δ HJI), в который вписана окр-ть в точке K. Длина стороны HJ = 16 см, JI = 9,5 см и сторона HI равна 19 см (рисунок 4). Найти радиус вписанной окр-ти, зная стороны.

Рисунок 4. Поиск значения радиуса вписанной окружности

Решение: для нахождения радиуса вписанной окр-ти найдем полупериметр:

Отсюда, зная механизм вычисления, узнаем следующее значение. Для этого понадобятся длины каждой из сторон (дано по условию), а также половину периметра, получается:

Отсюда следует, что искомый радиус равен 3,63 см. Согласно условию, все стороны равны, тогда искомый радиус будет равен:

При условии, если многоугольник равнобокий (например, i = h = 10 см, j = 8 см), диаметр внутренней окр-ти с центром в точке K будет равен:

В условии задачи может даваться треугольник с углом 90°, в таком случае запоминать формулу нет необходимости. Гипотенуза треугольника будет равна диаметру. Более наглядно это выглядит так:

Важно! Если задана задача на поиск внутреннего радиуса, не рекомендуем проводить вычисления через значения синусов и косинусов углов, табличное значение которых точно не известно. В случае, если иначе узнать длину невозможно, не пытайтесь «вытащить» значение из-под корня. В 40% задач полученное значение будет трансцендентным (т.е. бесконечным), а комиссия может не засчитать ответ (даже если он будет правильным) из-за его неточности или неправильной формы подачи. Особое внимание уделите тому, как может видоизменяться формула радиуса описанной окружности треугольника в зависимости от предложенных данных. Такие «заготовки» позволяют заранее «видеть» сценарий решения задачи и выбрать наиболее экономное решение.

Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Радиус внутренней окружности и площадь

Для того чтобы вычислить площадь треугольника, вписанного в окружность, используют лишь радиус и длины сторон многоугольника:

Если в условии задачи напрямую не дано значение радиуса, а только площадь, то указанная формула площади трансформируется в следующую:

Рассмотрим действие последней формулы на более конкретном примере. Предположим, что дан треугольник, в который вписана окр-ть. Площадь окр-ти составляет 4π, а стороны равны соответственно 4, 5 и 6 см. Вычислим площадь заданного многоугольника при помощи вычисления полупериметра.

Используя вышеуказанный алгоритм, вычислим площадь треугольника через радиус вписанной окружности:

В силу того, что в любой треугольник можно вписать окружность, число вариаций нахождения площади значительно увеличивается. Т.е. поиск площади треугольника, включает в себя обязательное знание длины каждой стороны, а также значение радиуса.

Треугольник, вписанный в окружность геометрия 7 класс

Прямоугольные треугольники, вписанные в окружность

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Вывод

Из указанных формул можно убедиться, что сложность любой задачи с использованием вписанной и описанной окружностей заключается только в дополнительных действия по поиску требуемых значений. Задачи подобного типа требуют только досконально понимания сути формул, а также рациональности их применения. Из практики решения отметим, что в будущем центр описанной окружности будет фигурировать и в дальнейших темах геометрии, поэтому запускать ее не следует. В противном случае решение может затянуться с использованием лишних ходов и логических выводов.

💥 Видео

Прямоугольные треугольники, вписанные в окружностьСкачать

КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

1 2 4 сопряжение окружностейСкачать

Д.О. Технология 8 кл. Аксонометрическая проекция плоскогранных предметов. И.М.МазаеваСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Изображение фигур в параллельной проекции. Решение задач. Часть 2Скачать