Цель состоит в том, чтобы построить круг, используя центральную точку и радиус в MATLAB без использования встроенных функций для построения графика. Черно-белое изображение может быть представлено в виде матрицы 2 порядка. Первый порядок для строк, а второй порядок для столбцов, значение пикселя будет определять цвет пикселя на основе цветового формата оттенков серого.
Подходить :
- Нам даны точка и радиус. Пусть координаты центральной точки (x1, y1) и радиус — R.
- Мы находим расстояние от центральной точки до каждого пикселя (i, j) th.
- Теперь, если dist = R, т.е. радиус, мы делаем этот пиксель черным.
Ниже приведена реализация:
Код% MATLAB для построения круга с использованием центра и радиуса.
% создать белое изображение размером 300X600
I=zeros(300, 600)+1;
% Радиус окружности
R=50;
% координаты центральной точки
c=300;
r=150;
% доступ к каждому пикселю
% отображать изображение
figure, imshow(I);
Выход :
- Построить график окружности в матлабе
- Л-22 Элементы графической визуализации
- Содержание
- Графика в Mathcad
- Графика в Matlab
- Построение графика функций одной переменной
- Построение в одном окне графиков нескольких функций
- Графическая функция fplot
- Столбцовые диаграммы
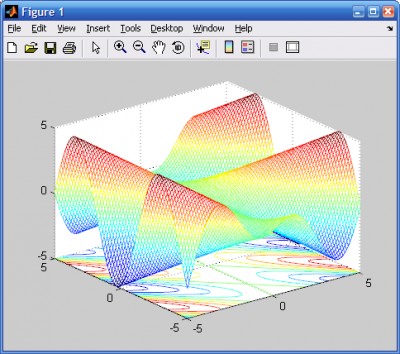
- Построение трехмерных графиков
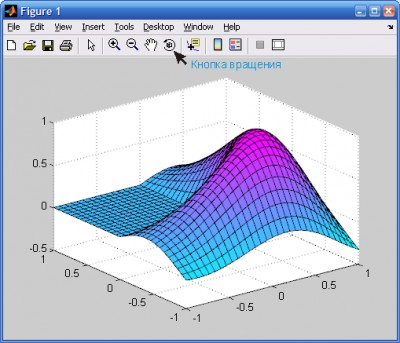
- Вращение графиков мышью
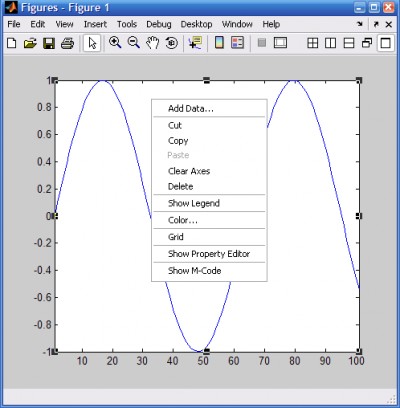
- Контекстное меню графиков
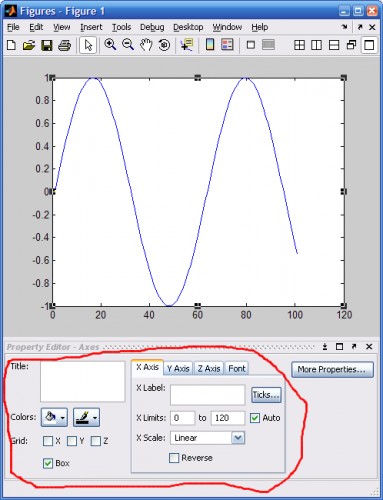
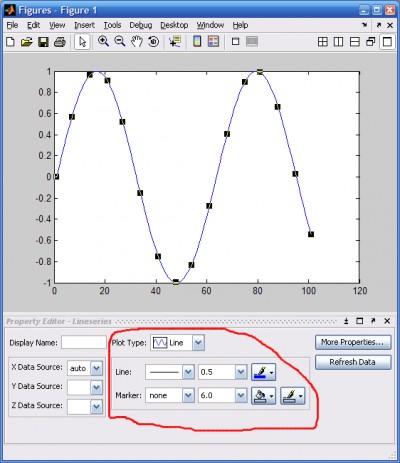
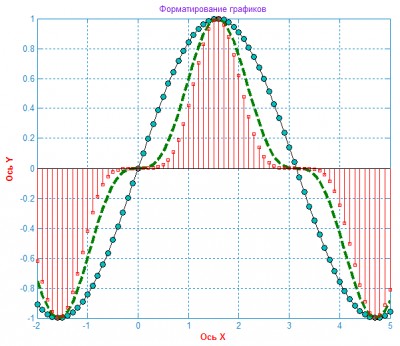
- Форматирование свойств графиков
- Форматирование линий и маркеров для графика нескольких функций
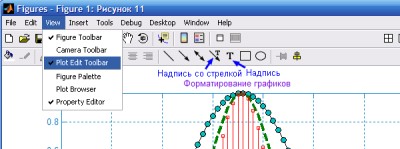
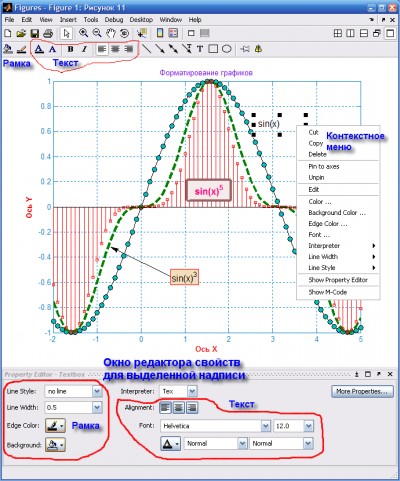
- Нанесение надписей и стрелок на график
- Построение легенды на графике
- 🎦 Видео
Видео:Как оформить график в MatLab.Скачать

Построить график окружности в матлабе
Обычная графика MATLAB
Построение графиков точками и отрезками прямых
Графики в логарифмическоми полулогарифмическом масштабе
Гистограммы и диаграммы
Графики специальных типов
Создание массивов данных для трехмерной графики
Построение графиков трехмерных поверхностей, сечений и контуров
Средства управления подсветкой и обзором фигур
Средства оформления графиков
Одновременный вывод нескольких графиков
Управление цветовой палитрой
Окраска трехмерных поверхностей
Двумерные и трехмерные графические объекты
Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса (GUI). Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов.
Описанию графических функций и команд посвящена обширная электронная книга в формате PDF. Объем материала по графике настолько велик, что помимо вводного описания графики в уроке 3 в этой книге даются еще два урока по средствам обычной и специальной графики. Они намеренно предшествуют систематизированному описанию большинства функций системы MATLAB, поскольку графическая визуализация вычислений довольно широко используется в последующих материалах книги. При этом графические средства системы доступны как в командном режиме вычислений, так и в программах. Этот урок рекомендуется изучать выборочно или выделить на него не менее 4 часов.
Построение графиков отрезками прямых
Функции одной переменной у(х) находят широкое применение в практике математических и других расчетов, а также в технике компьютерного математического моделирования. Для отображения таких функций используются графики в декартовой (прямоугольной) системе координат. При этом обычно строятся две оси — горизонтальная X и вертикальная Y, и задаются координаты х и у, определяющие узловые точки функции у(х). Эти точки соединяются друг с другом отрезками прямых, т. е. при построении графика осуществляется линейная интерполяция для промежуточных точек. Поскольку MATLAB — матричная система, совокупность точек у(х) задается векторами X и Y одинакового размера.
Команда plot служит для построения графиков функций в декартовой системе координат. Эта команда имеет ряд параметров, рассматриваемых ниже.
plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.
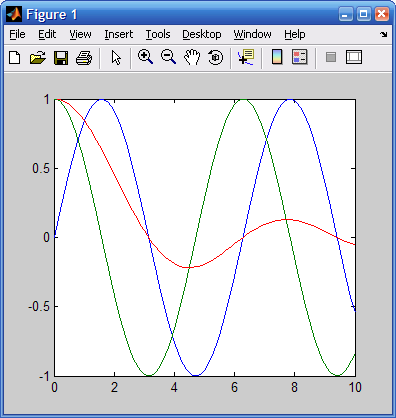
Приведенный ниже пример иллюстрирует построение графиков двух функций — sin(x) и cos(x), значения функции которых содержатся в матрице Y, а значения аргумента х хранятся в векторе X:
На рис. 6.1 показан график функций из этого примера. В данном случае отчетливо видно, что график состоит из отрезков, и если вам нужно, чтобы отображаемая функция имела вид гладкой кривой, необходимо увеличить количество узловых точек. Расположение их может быть произвольным.
Рис. 6.1. Графики двух функций в декартовой системе координат
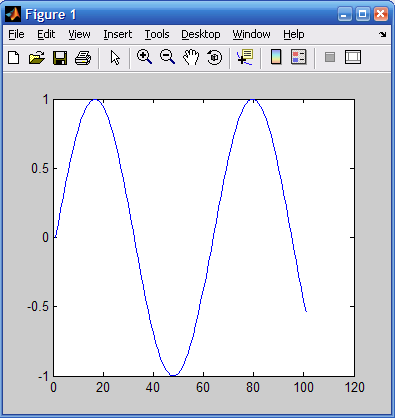
plot(Y) — строит график у(г), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Y содержит комплексные элементы, то выполняется команда plot (real (Y). imag(Y)). Во всех других случаях мнимая часть данных игнорируется.
Вот пример использования команды plot(Y):
Соответствующий график показан на рис. 6.2.
Рис. 6.2. График функции, представляющей вектор Y с комплексными элементами
plot(X.Y.S) — аналогична команде plot(X.Y), но тип линии графика можно задавать с помощью строковой константы S.
Значениями константы S могут быть следующие символы.
Видео:MatLab. Урок 3. Функции и построение графиков.Скачать

Л-22 Элементы графической визуализации
| Лекции: Введение | Л-1: Краткая история компьютерной графики. Основные понятия о машинной графике и основные задачи компьютерной графики. Классификация направлений и сферы применения компьютерной графики. Задачи курса | Л-2: Программное обеспечение для создания, просмотра и обработки графической информации | Л-3: Текстовый редактор. Работа с текстом (простой и фигурный, вдоль кривой, эффекты для текста) | Л-4: Презентация и анимация графических и текстовых объектов. Средства организации чертежа (система координат, единицы измерения, слои, графические примитивы) | Л-5: Основные понятия о растровом и векторном изображении. Прикладное назначение программ для графического отображения физических процессов. Виды программного обеспечения для графики математического моделирования | Л-6: Виды графических программ векторной графики: Microsoft Visio, Corеl Draw, АutoCAD | Л-7: Окна программ векторной графики. Особенности импорта и экспорта изображений и макетов | Л-8: Панель инструментов программы. Библиотека элементов векторной графики | Л-9: Системы цветов в компьютерной графике: HSB, HSL, RGB, CMYK | Л-10: Методика рисования простых фигур и векторный способ формирования графических объектов | Л-11: Линии как объект векторной графики и их свойства | Л-12: Виды графических программ растровой графики: Pаint, Adobe Photoshop. Понятие слоя, создание изображения со слоями; копирование, перемещение, наложение, удаление слоев | Л-13: Двумерные (2D) и трехмерные (3D) геометрические преобразования в компьютерной графике | Л-14: Масштабирование изображений. Панели инструментов программ Pаint, Adobe Photoshop и др. | Л-15: Растровый способ формирования графических образов | Л-16: Вставка и редактирование рисунков. Геометрическое моделирование, преобразования растровых и векторных изображений | Л-17: Выделение и трансформация областей. Работа с текстом | Л-18: Тональная и цветовая коррекция и фильтры. Маски, каналы и ретушь | Л-19: Смешивание слоев, эффекты и стили слоев | Л-20: Виды систем графического моделирования: Mathсad, MatLab. Интерфейс пользователя систем Mathсad и MatLab | Л-21: Работа со встроенными функциями, массивами, векторами и матрицами | Л-22: Элементы графической визуализации. Графическая визуализация вычислений — построение графиков функций | Л-23: Основы работы с векторами и матрицами. Палитры математических знаков и документы Mathсad | Дополнительные материалы: |