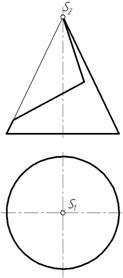
Построить фронтальную проекцию треугольника abc лежащего в плоскости заданной параллельными прямыми

Видео:Построение следов плоскостиСкачать

Плоскость. Прямая и точка в плоскости.

Задача № 13 Построить следы плоскости, заданной пересекающимися прямыми l и c.

Задача № 14. Построить недостающие проекции точек А и В, лежащих в плоскости, заданной пересекающимися прямыми.

Задача № 15 Построить фронтальную проекцию треугольника АВ С, расположенного в плоскости а .

Задача №1 6 Построить горизонтальную проекцию треугольника АВ С в плоскости, заданной пересекающимися прямыми.

Задача №1 7 Достроить фронтальную проекцию плоского четырехугольника ABCD

Задача № 20 Определить угол наклона данной плоскости к плоскости проекций

Видео:Построить недостающую проекцию треугольника АВС, лежащего в плоскости, заданной параллельными прямымСкачать

ПРИМЕРЫ РЕШЕНИЯ ИНДИВИДУАЛЬНЫХ заданий

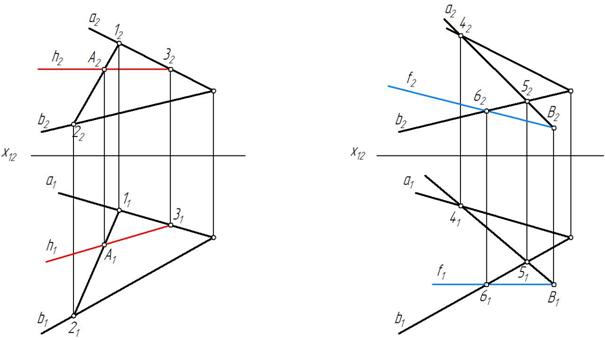
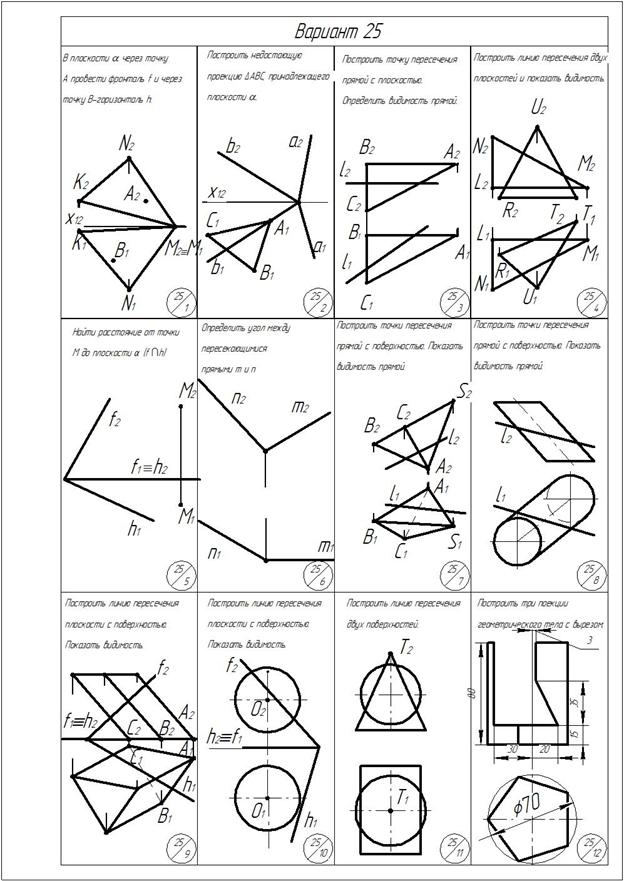
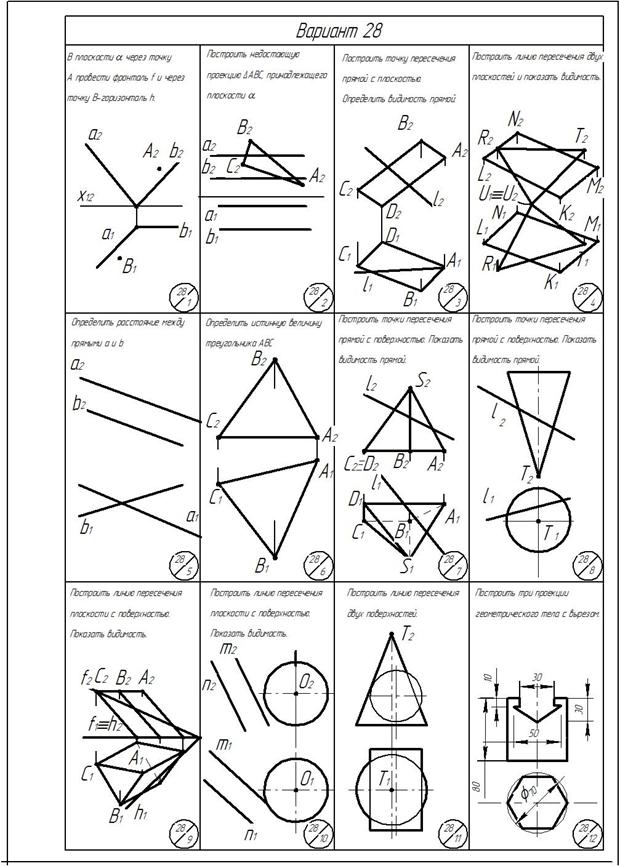
Задача 1.В плоскости α(а∩в) через точку А провести горизонталь h и через точку В-фронталь f (рис. 229).

Прямая принадлежит плоскости, если она имеет с ней две общие точки или имеет одну общую точку и параллельна прямой этой плоскости.

Находим фронтальную проекцию точки А. Для этого через горизонтальную проекцию А₁ точки А проводим горизонтальную проекцию1₁-2₁ произвольной прямой 1-2, принадлежащей заданной плоскости α(а∩в). На фронтальной проекции 1₂-2₂ прямой 1-2 отмечаем А₂. Через фронтальную проекцию А₂ точки А проводим параллельно оси х₁₂ фронтальную проекцию h₂ горизонтали h. Затем через точки 3₁ и А₁ проводим горизонтальную проекцию горизонтали h₁ (рис. 230, а).

Находим горизонтальную проекцию точки В. Для этого проводим фронтальную проекцию 4₂-5₂ произвольной прямой 4-5, принадлежащей заданной плоскости α(а∩в). На горизонтальной проекции 4₁-5₁ прямой 4-5 отмечаем В₁. Через горизонтальную проекцию В₁ точки В проводим параллельно оси х₁₂ горизонтальную проекцию f₁ фронтали f. Затем через точки В₂ и 6₂ проводим фронтальную проекцию фронтали f₂ (рис. 230, б).

Задача 2.

Пример 1. Построить фронтальную проекцию треугольника АВС, принадлежащего плоскости α(f∩h) (рис. 231).

Точка принадлежит плоскости, если она находится на прямой, принадлежащей этой плоскости. В качестве прямых, принадлежащих плоскости, удобно воспользоваться главными линиями плоскости – горизонталью h или фронталью f.

Рис. 232 Рис. 233

Строим фронтальную проекцию С₂ точки С. Для этого через горизонтальную проекцию С₁ проводим горизонтальную проекцию фронтали параллельно оси х ₁₂. Строим фронтальную проекцию фронтали параллельно f ₂ и отмечаем на ней фронтальную проекцию С₂ (рис. 232).

Аналогично строим фронтальную проекцию В₂. Строим фронтальную проекцию точки А ₂ на h₂. Соединяем А₂В₂С₂ и получаем недостающую фронтальную проекцию треугольника АВС (рис. 233).

Пример 2. Построить фронтальную проекцию треугольника АВС, принадлежащего плоскости α(ΔМ NK) (рис. 234).

Рис. 234 Рис. 235

Точка В принадлежит прямой М K, отмечаем фронтальную проекцию В₂ на фронтальной проекции прямой М K. Затем отмечаем точку 1₁ на пересечении горизонтальных проекций прямых AB и MN. По линии связи отмечаем 1₂ на M₂N₂ и через точки В₂ и 1₂ проводим прямую и на ней отмечаем М₂. Построение точки С₂ понятно из чертежа (рис. 235)

Задача 3.

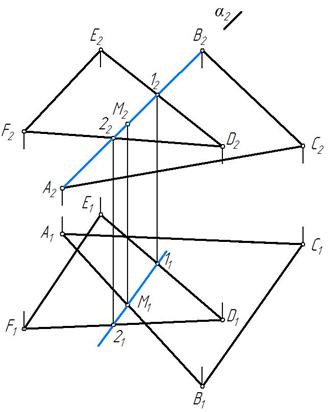
Пример 1. Найти точку пересечения прямой l плоскостью α(а‖b) (рис. 236).

Рис. 236 Рис. 237

Плоскость α, заданная параллельными прямыми, является плоскостью общего положения. Проводим через прямую l вспомогательную плоскость β^П₂. Строим линию пересечения плоскостей заданной α и вспомогательной β – это будет прямая 1-2. В месте пересечения горизонтальных проекций l ₁ и 1₁2₁ отмечаем горизонтальную проекцию K₁. Фронтальную проекцию K₂ точки K находим по принадлежности точки K прямой l (рис. 237). Видимость прямой не отмечаем.

Пример 2. Найти точку пересечения прямой l плоскостью α(m ∩ n) (рис. 238).

Рис. 238 Рис. 239

Плоскость α(m∩n) является плоскостью общего положения. Проведем через прямую l вспомогательную плоскость β‖П₁. Линией пересечения, заданной α и вспомогательной плоскости β будет горизонталь, проведенная параллельно горизонтали n. Дальнейшее построение понятно из чертежа (рис. 239).

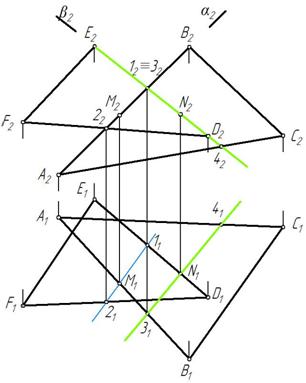
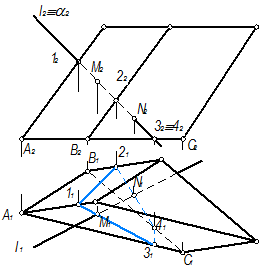
Задача 4. Построить линию пересечения DАВС и DDEF(рис. 240).

Чтобы построить линию пересечения двух треугольников, необходимо найти точки пересечения двух прямых, принадлежащих одной из плоскостей, с другой плоскостью.

Находим точку пересечения стороны АВ с плоскостью ΔDEF. Для этого через прямую АВ проводим вспомогательную фронтально-проецирующую плоскость α. Строим линию 1-2 пересечения вспомогательной плоскости α с ΔDEF и отмечаем на пересечении с АВ искомую точку М (рис. 241).

Аналогичным образом, через прямую DE проводим фронтально-проецирующую плоскость β. Строим линию 3-4 пересечения плоскости β с ΔАВС и отмечаем на пересечении с DE искомую точку N (рис. 242).

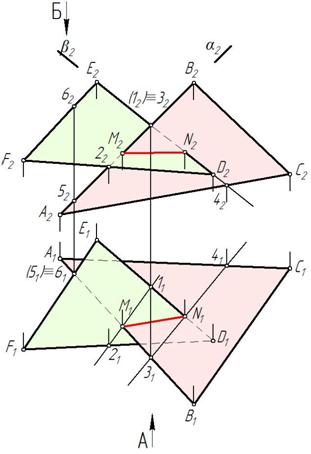
Прямая МN искомой линии пересечения плоскостей двух треугольников построена на рис.243.

Определяем видимость треугольников на П₂. Для этого на П₂ сравниваем видимость скрещивающихся прямых АВ и D Е. Отметим точки 3∈АВ, 1∈D Е. Горизонтальная проекция 3₁ находится перед 1₁ (направление взгляда А). Невидимая точка 1₂ закрыта в скобки (рис. 244). Следовательно, прямая А₂В₂ видима до М₂, а часть прямой А₂В₂ закрывается плоскостью DEF.

Определяем видимость треугольников на П₁. Для этого сравниваем видимость скрещивающихся прямых АВ и ЕF. Отмечаем точки 5∈АВ, 6∈EF. Фронтальная проекция 6₂ находится выше 5₂ (направление взгляда Б). Следовательно, E ₁ F ₁ видима, а закрывается часть прямой А₁В₁ до точки М₁ (рис. 244).

Задача 5.

Пример 1. Определить расстояние от точки А до прямой l (рис. 245).

Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую.

На эпюре проекции перпендикуляра к прямой можно построить, если прямая параллельна плоскости проекций. Поэтому сначала строим дополнительную ортогональную проекцию прямой и точки А на плоскости П₄, параллельной прямой l и перпендикулярной к П₁. При этом ось х₁₄ параллельна l ₁ . Для построения дополнительной проекции прямой l на ней отмечены точки 1 и 2 (рис. 246).

2. Проводим дополнительную проекцию А₄ K ₄ перпендикуляра (А₄ K ₄ l ₄), а затем строим горизонтальную проекцию А ₁ K ₁ . Построена также и фронтальная А ₂ K ₂ проекция перпендикуляра АK (рис. 247).

Отрезок АK – общего положения. По двум данным проекциям отрезка АK (А ₁ K ₁ и А ₄ K ₄) находим его длину, построив дополнительную ортогональную проекцию отрезка на плоскости П₅, параллельной АK и перпендикулярной к П₄. Ось х₄₅ параллельна А₄K₄ (рис. 247).

Аналогично можно определить расстояние между двумя параллельными прямыми. Для этого возьмем на одной прямой любую точку и найдем расстояние от этой точки до второй прямой.

Пример 2. Определить расстояние от точки А до плоскости α (f∩h) (рис. 248).

Расстоянием от точки до плоскости является длина отрезка перпендикуляра, опущенного из точки на плоскость.

Если плоскость является проецирующей, то перпендикуляр к ней параллелен плоскости проекций и длина проекции его отрезка на этой плоскости проекций равна искомому расстоянию. Исходя из этого построим дополнительную ортогональную проекцию плоскости α и точки А на плоскости, перпендикулярной к плоскости α и к плоскости П₁.

Плоскость П₄ будет перпендикулярна к плоскости α, если она перпендикулярна к горизонтали этой плоскости. При этом ось х₁₄ перпендикулярна к горизонтальной проекции h ₁ горизонтали h плоскости α. Дополнительной ортогональной проекцией плоскости α на плоскость П₄ является прямая f₄. Для ее построения отметили произвольную точку 1 и построили ее дополнительную проекцию 1₄.

Из точки А₄ опускаем перпендикуляр А₄ K ₄ на прямую f₄. Длина отрезка А₄ K ₄ равна расстоянию от точки А до плоскости α(ΔBCD).

Построим проекции отрезка АК. Горизонтальная проекция А₁ K ₁ параллельна оси х₁₄, так как отрезок АK параллелен плоскости П₄, и перпендикулярна к горизонтальной проекции h ₁ горизонтали h плоскости α. Фронтальную проекцию А₂ K ₂ строим перпендикулярно фронтальной проекции фронтали f₂. Поэтапное решение показано на (рис. 249).

На основании решения рассмотренной задачи можно определить расстояние между параллельными прямой и плоскостью, между двумя параллельными плоскостями.

Задача 6.Определить натуральную величину угла между двумя пересекающимися прямыми (рис. 250).

Рис. 250 Рис. 251

Угол между двумя пересекающимися прямыми спроецируется без искажения на плоскость проекций, параллельную плоскости α(m⋂n). Но сразу выбрать плоскость параллельную плоскости угла и перпендикулярную плоскостям проекций невозможно. Поэтому сначала построим дополнительную ортогональную проекцию плоскости α(m⋂n) на плоскость ей перпендикулярную П₄^α(m⋂n) и П₄^П₁. Для этого в плоскости α(m⋂n) проводим горизонталь h и перпендикулярно ей строим ось х₁₄. Плоскость α спроецируется в прямую линию (рис. 251).

Затем строим дополнительную ортогональную проекцию плоскости α(m⋂n) на плоскость ей параллельную П₅‖α(m⋂n) и П₅^П₄. Ось х₄₅ проведена параллельно α₄. Угол между m ₅ и n ₅ равен искомому углу φ (рис. 252).

Задача 7. Построить точки пересечения прямой l с поверхностью призмы. Определить видимость прямой (рис. 253).

Через прямую l проводим фронтально-проецирующую плоскость α^П₂, l₂ ≡ α₂. Строим линию пересечения плоскости α с поверхностью призмы. На фронтальной проекции отметим 1₂, 2₂, в которых α₂ пересекает проекции ребер, а также 3₂ и 4₂ на основании. Горизонтальные проекции 1₁, 2₁, 3₁, 4₁ отмечаем на соответствующих проекциях ребер. Соединяем горизонтальные проекции 1₁, 2₁, 3₁, 4₁ ломаной линией с учетом видимости. Боковая грань, примыкающая к ребру ВС основания на горизонтальной проекции невидима, так как это ребро невидимо. Следовательно, отрезок 2₁-4₁ также не видим (рис. 254).

На пересечении горизонтальной проекции l ₁ с горизонтальной проекцией 1₁-2₁-3_1--4₁ отмечаем горизонтальные проекции M ₁ и N ₁ точек М и N.

Строим фронтальные проекции M ₂ и N ₂ на l ₂ по линии связи.

Определяем видимость прямой l. Между полученными точками M и N на обеих проекциях прямая l невидима всегда. Горизонтальная проекция l ₁ невидима между M ₁ N ₁ и от N ₁ до выхода за очерк призмы, так как горизонтальная проекция N ₁ принадлежит невидимой относительно П₁ грани ВС.

На П₂: точка М находится на грани A С невидимой относительно П₂, следовательно, М ₂ невидима и фронтальная проекция l ₂ невидима до ребра. Точка N принадлежит грани В C, видимой относительно П₂, следовательно, фронтальная проекция N ₂ видима и фронтальная проекция l ₂ от N ₂ видима. За очерками призмы прямая l видима (рис. 255).

Рис. 254 Рис. 255

Задача 8. Построить точки пересечения прямой l с поверхностью цилиндра. Определить видимость прямой (рис. 256).

Для нахождения точек пересечения прямой с поверхностью необходимо через прямую провести вспомогательную плоскость такую, чтобы она пересекала поверхность цилиндра по простым линиям. Проведем плоскость, параллельную оси цилиндра. Зададим ее параллельными прямыми. Эта плоскость пересекает заданную поверхность по образующим.

На прямой l возьмем произвольные точки А (А₁, А₂) и В (В₁, В₂). Через эти точки проведем прямые а и в, параллельные оси цилиндра.

Строим линию пересечения вспомогательной плоскости с плоскостью основания цилиндра. Это прямая линия α₁ (рис. 257).

Строим горизонтальные проекции образующих, которые проходят через горизонтальные проекции 1₁ и 2₁ точек 1 и 2 пересечения плоскости α с основанием поверхности цилиндра.

На пресечении горизонтальных проекций образующих и прямой l находим горизонтальныепроекции М₁ и N₁ искомых точек пересечения М и N, а по ним строим фронтальные проекции М₂ и N₂ этих точек.

Определяем видимость прямой l. Между полученными точками прямая всегда невидима. Видимость точек М и N определяем по видимости образующих, на которых находятся эти точки (рис. 258).

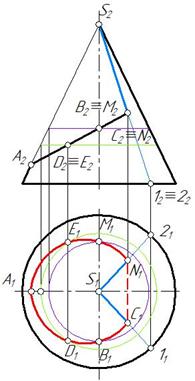
Задача 9. Построить линию пересечения плоскости δ(f∩h) c поверхностью пирамиды (рис. 259).

Линия пересечения в данном случае – замкнутая ломаная линия. Для ее построения необходимо найти точки пересечения ребер призмы с заданной плоскостью.

Чтобы найти точку М, в которой ребро A D призмы пересекает плоскость α(f∩h), через ребро A D проводим вспомогательную плоскость β^П₂. Затем строим линию пересечения вспомогательной плоскости с заданной (это прямая 1-2). Прямая 1-2 пересекается с ребром A D в точке М (М₁, М₂) (рис. 260).

Аналогично определены точки N и L, в которых ребра СЕ, BF пересекают плоскость α(f∩h).

Полученные точки М, N и L соединяем отрезками прямых с учетом видимости. Видимость устанавливаем по видимости граней призмы (рис. 261).

Рис. 260 Рис. 261

Задача 10.

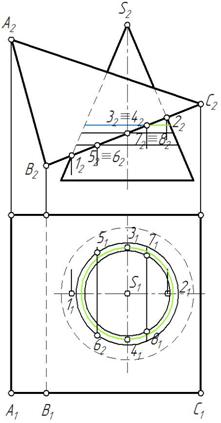
Пример1. Построить линию пересечения плооскости α(f ∩ h ) с цилиндрической поверхностью (рис. 262).

Линия персечения заданной плоскости α с цилиндрической поверхностью будет эллипс. Для построения линии пересечения найдем ряд ее точек, как точек пересечения образующих поверхности цилиндра сплоскостью.

Строим опорные точки на очерковых образующих (точки А, В, С, D). Для нахождения точки А на очерковой образующей, обозначенной точкой 1, через нее проводим вспомогательную плоскость β^П₂. Затем строим линию пересечения вспомогательной плоскости β с заданной плоскостью α(f ∩ h ) – это прямая 2-3. Образующая 1 и прямая 2-3 пересекаются в искомой точке А(А₁, А₂) (рис. 263).

Рис. 263 Рис. 264

Аналогично строим остальные точки линии персечения. На рис. 263 показано построение точки В. При построении горизонтальной проекции линии пересечения вспомогательной плоскости γ с плоскостью α(f ∩ h) пользуемся тем, что фронтальная проекция прямой 2-3 параллельна фронтальной проекции прямой 4-5, значит параллельны и горизонтальные проекции этих прямых. На рис. 265 показано построение точек С и D.

Рис. 265 Рис. 266

Строим также промежуточные точки E, F, G, H на произвольных образующих. Полученные точки соединяем плавной кривой с учетом видимости. Видимость линии пересечения устанавливаем по видимости одной точки, например F, лежащей на образующей 8, которая видима как относительно плоскости проекций П₁, так относительно плоскости проекций П₂. В точках касания эллипса с очерковыми образующими видимость эллипса изменяется (рис. 266).

Пример 2. Построить линию пересечения конуса с плоскостью α(f ∩ h )(рис. 267.)

Заданная плоскость общего положения. Линией пересечения будет часть эллипса, ограниченная прямой. Поскольку основание и горизонталь находятся на горизонтальной плоскости проекций отметим общие точки их пересечения – А и В. Найдем точку пересечения очерковой образующей с заданной плоскостью α. Для этого проводим через точку 1 фронталь в заданной плоскости α . Фронталь пересекает очерковую образующую в точке С (рис. 268)

Рис. 268 Рис. 269

Для нахождения самой высокой точки линии пересечения проведем вспомогательную плоскость β перпендикулярную горизонтали h плоскости α .Образующая S 5 в точке D пресекается с прямой 3-4, являющейся линией пресечения плоскостей α и β (рис. 269).

Для нахождения промежуточных точек линии пересечения проведем вспомогательную горизонтальную плоскость γ. Плоскость γ пересекает конус по окружности, а плоскость α по горизонтали,проходящей через точку 6. В месте пересечения горизонтали и окружности отмечаем точки Е и F.

Полученные точки АЕСD FB соединяем с учетом видимости (рис. 270).

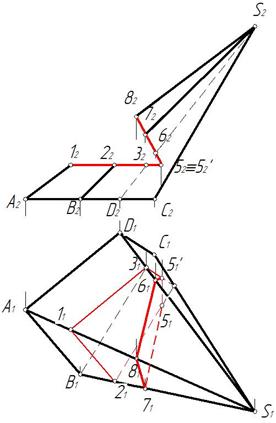
Задача 11. Построить линию пересечения призмы с конусом (рис. 271).

Поверхность призмы занимает фронтально-проецирующее положение. Грань АВ не пересекает конус.

Грани АС и ВС призмы пересекут конус по эллипсам. Для построения эллипсов надо взять ряд точек на грани и построить их горизонтальные проекции. Точки 1 и 2, 9 и 10 отмечены на очерковых образующих конуса, остальные находятся на окружностях, проведенных на поверхности конуса (рис. 272, 273).

Рис. 272 Рис. 273

Полученные точки соединяем плавными кривыми. Видимость эллипсов определяется видимостью граней. Грань АС видима относительно плоскости проекций П₁, следовательно, эллипс 9₁-11₁-10₁-12₁ видим. Грань призмы ВС невидима относительно плоскости П₁, следовательно, эллипс 1₁-5₁-3₁-7₁-2₁-8₁-4₁-6₁-1₁ не видим (рис. 273). Определена также видимость очерков поверхностей.

Задача 12

Пример 1. Построить три проекции выреза на конусе (рис. 274).

Вырез произведен двумя фронтально-проецирующими плоскостями. Плоскость α проходит через вершину конуса и пересечет его поверхность по образующим – двум прямым. Вторая плоскость β – фронтально-проецирующая, линия пересечения – часть эллипса, ограниченная прямой принадлежащей линии пересечения плоскостей α и β – CN (рис. 275).

Отметим фронтальные проекции характерных точек для построения выреза – А ₂, В ₂, С ₂, M ₂, N ₂ (рис. 275).

Рис. 275 Рис. 276

Точки D и Е выбираем произвольно для построения эллипса, так как линия среза от А до С N представляет собой часть эллипса.

Находим горизонтальные проекции точек А, В, С, D , Е, N. Точки находятся на поверхности конуса, а значит, они лежат линиях, принадлежащих поверхности конуса. Горизонтальные проекции точек М и В, D и E находим на окружностях, принадлежащих поверхности конуса. Точки С и N – на образующих S 1 и S 2.

Строим профильную проекцию конуса и профильные проекции точек. Соединяем их (рис. 277). Очерковая образующая удалена отМ₃ до S₃.

Пример 2. Построить горизонтальную проекцию выреза на наклонной пирамиде (рис. 278).

Рис. 278 Рис. 279

Рис. 280 Рис. 281

Поэтапное решение показано на рис. 279–281.

Пример 3. Построить горизонтальную проекцию выреза на цилиндре (рис. 282).

Рис. 282 Рис. 283

Рис. 284 Рис. 285

Список литературы

1. Гордон В. О. Курс начертательной геометрии / В. О. Гордон, М. А. Семенцов-Огиевский. – М. : Наука, 2000. – 272 с.

2. Крылов Н. Н. Начертательная геометрия / Н. Н. Крылов. – М. : Высшая школа, 2007. – 224 с.

3. Локтев О. В. Краткий курс начертательной геометрии / О. В. Локтев – М. : Высшая школа, 2001. – 130 с.

4. Фролов С. А. Начертательная геометрия / С. А. Фролов – М. : Машиностроение, 1983. – 240 с.

Приложение

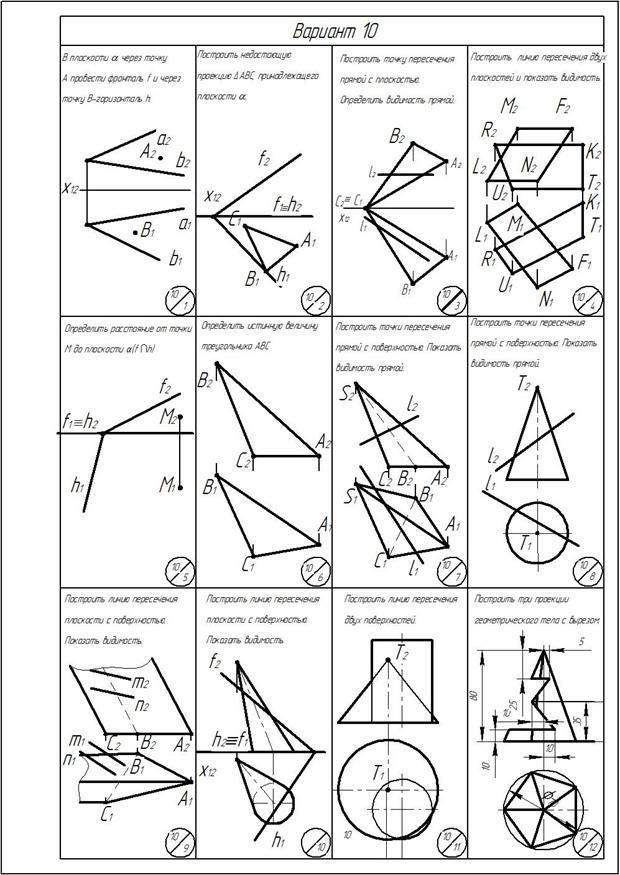
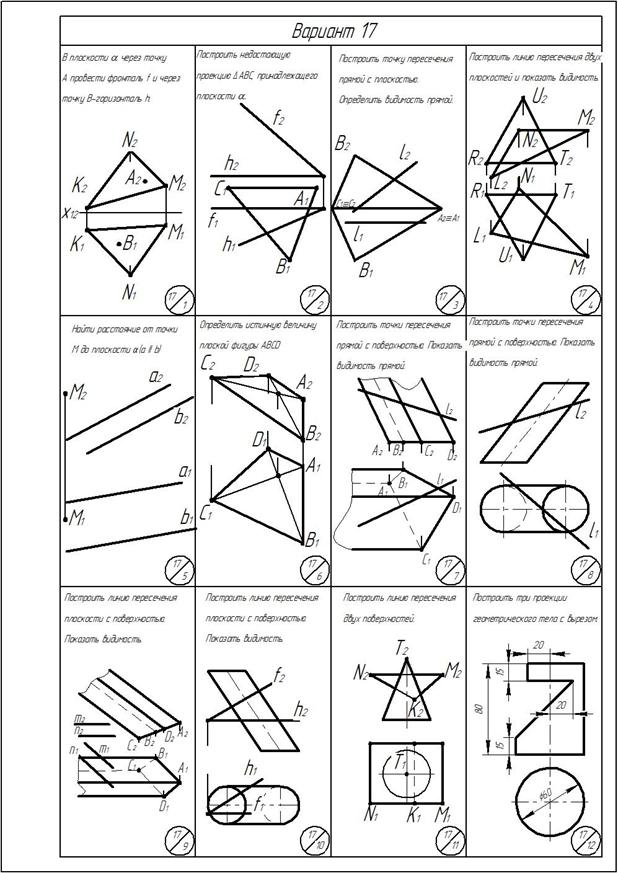
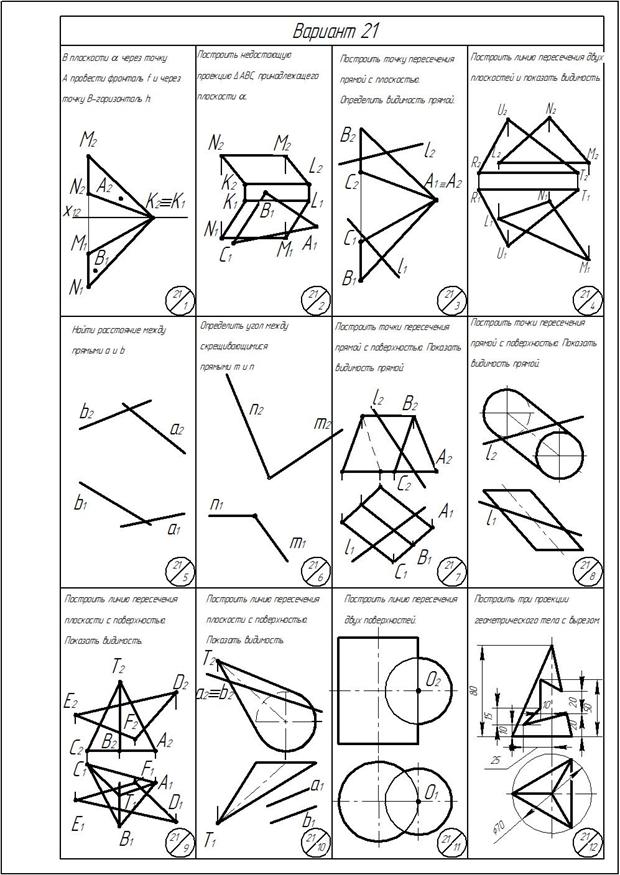
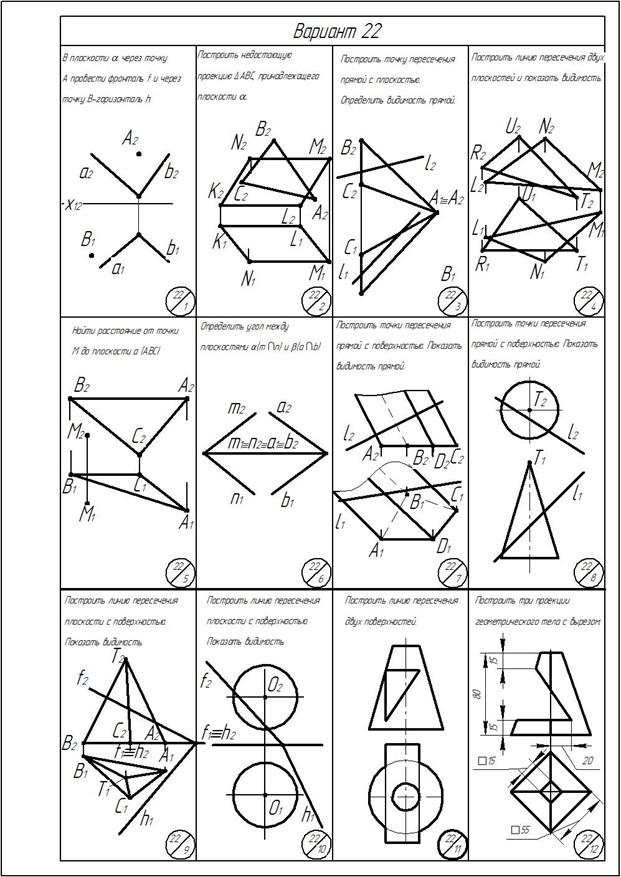
ОГЛАВЛЕНИЕ

Леонова Ольга Николаевна,

Разумнова Елена Александровна

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.

Решение типовых задач

Подписано к печати .2018. Формат 60´84 1/16. Бум. офсетная.

Усл. печ. л. . Тираж 100 экз. Заказ . «С» .

Санкт-Петербургский государственный архитектурно-строительный университет.

Видео:Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Построить фронтальную проекцию треугольника abc лежащего в плоскости заданной параллельными прямыми

Плоскостью называется поверхность, образуемая движением прямой линии, которая движется параллельно самой себе по неподвижной направляющей прямой .

Проекции плоскости на комплексном чертеже будут различны в зависимости от того, чем она задана. Как известно из геометрии, плоскость может быть задана: а) тремя точками, не лежащими на одной прямой; б) прямой линией и точкой, лежащей вне этой прямой; в) двумя пересекающимися прямыми; г) двумя параллельными прямыми.

На комплексном чертеже (рис. 99) проекции плоскости также задаются проекциями этих элементов, например, на рис 99, а — проекциями трех точек А, , и С, не лежащих на одной прямой; на рис. 99, б — проекциями прямой ВС и точки А у не лежащей на этой прямой; на рис. 99, в — проекциями двух пересекающихся прямых; на рис. 99, г проекциями двух параллельных прямых линий АВ и CD.

На рис. 100 плоскость задана прямыми линиями, по которым эта плоскость пересекает плоскости проекций. Такие линии называются следами плоскости.
Линия пересечения данной плоскости Р с горизонтальной плоскостью проекций Н называется горизонтальным следом плоскости Р и обозначается Р_н.
Линия пересечения плоскости Р с фронтальной плоскостью проекций V называется фронтальным следом этой плоскости и обозначается Р_v.

Линия пересечения плоскости Р с профильной плоскостью проекций W называется профильным следом этой плоскости и обозначается P_w.

Следы плоскости пересекаются на осях проекций. Точки пересечения следов плоскости с осями проекций называются точками схода следов. Эти точки обозначаются Р_x, Р_y и Р_z.

Расположение следов плоскости Р на комплексном чертеже по отношению к осям проекций определяет положение самой плоскости по отношению к плоскостям проекций. Например, если плоскость Р имеет фронтальный и профильный следы P_v и P_w, параллельные осям Ох и Оу то такая плоскость параллельна плоскости Н и называется горизонтальной (рис. 101, и). Плоскость Р со следами Р_н и P_w , параллельными осям проекций Ох и Oz (рис. 101, называется фронтальной, а плоскость Р со следами P_v и P_н параллельными осям проекций Оу и Oz, — профильной (рис. 101, в).

Горизонтальная, фронтальная и профильная плоскости, перпендикулярные к двум плоскостям проекций, называются плоскостями уровня. Если на комплексном чертеже плоскость уровня задана не следами, а какой-нибудь плоской фигурой, например, треугольником или параллелограммом (рис. 101, г, д, е), то на одну из плоскостей проекций эта фигура проецируется без искажения, а на две другие плоскости проекций — в виде отрезков прямых.

ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ И ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ

Плоскость, перпендикулярная к плоскости Н (рис. 102, а),называется горизонтально-проецирующей плоскостью. Фронтальный след P_v этой плоскости перпендикулярен оси Ох, а горизонтальный след Р_н расположен под углом к оси Ох (комплексный чертеж на рис. 102, а)

Если горизонтально-проецирующая плоскость задана не следами, а какой-либо фигурой, например треугольником АВС (рис. 102, 6), то горизонтальная проекция этой плоскости представляет собой прямую линию, а фронтальная и профильная проекции — искаженный вид треугольника АВС.

Фронтально-проецирующей плоскостью называется плоскость, перпендикулярная к фронтальной плоскости проекций (рис. 102, в).

Горизонтальный след этой плоскости перпендикулярен оси Ох, а фронтальный след расположен под некоторым углом к оси Ох (комплексный чертеж на рис. 102, в).

При задании фронтально-проецирующей плоскости не следами, а, например, параллелограммом ABCD фронтальная проекция такой плоскости представляет собой прямую линию (рис. 102, г), а на горизонтальную и профильную плоскости проекций параллелограмм проецируется с искажением.

Профильно-проецирующей плоскостью называется плоскость, перпендикулярная к плоскости W (рис. 102, д). Следы P_v и Р_н этой плоскости параллельны оси Ох.

При задании профильно-проецирующей плоскости не следами, а, например, треугольником АВС (рис. 102, е) профильная проекция такой плоскости представляет собой прямую линию. Плоскости, перпендикулярные двум плоскостям проекций, как было сказано, называются плоскостями уровня.

Если плоскость Р не перпендикулярна ни одной из плоскостей проекций (рис. 102, ж), то такая плоскость называется плоскостью общего положения. Все три

следа P_v, Р_н и P_w плоскости Р наклонены к осям проекций.

Если плоскость общего положения задана не следами, а, например, треугольником АВС (рис. 102, з), то этот треугольник проецируется на плоскости H, V и W в искаженном виде.

ПРОЕКЦИИ ТОЧКИ И ПРЯМОЙ, РАСПОЛОЖЕННЫХ НА ПЛОСКОСТИ

Если прямая расположена на плоскости, то она должна проходить через две какие-либо точки, принадлежащие этой плоскости. Такие две точки могут быть взяты на следах плоскости — одна на горизонтальном, а другая на фронтальном. Так как следы прямой и плоскости находятся на плоскостях проекций и то следы прямой, принадлежащей плоскости, должны быть расположены на одноименных следах этой плоскости (рис. 103, а);например, горизонтальный след Н прямой — на горизонтальном следе плоскости, фронтальный след V прямой — на фронтальном следе Рv плоскости (рис. 103, б).

Для того чтобы на комплексном чертеже плоскости Р, заданной следами, провести какую-либо прямую общего положения, необходимо наметить на следах плоскости точки v’ или считать их следами искомой прямой (точнее, v’ — фронтальной проекцией горизонтального следа прямой).

Опустив перпендикуляры из v’ и на ось проекций х, находим на ней вторые проекции следов прямой: v — горизонтальную проекцию фронтального следа прямой и h’ — фронтальную проекцию горизонтального следа прямой. Соединив одноименные проекции следов, т. е. v’c h и v c h прямыми, получим две проекции прямой линии, расположенной в плоскости общего положения Р.

Очень часто требуется провести на плоскости горизонталь и фронталь, которые называются главными линиями плоскости или линиями уровня. Главные линии помогают решать многие задачи проекционного черчения.

Горизонталь и фронталь имеют в системе двух плоскостей V и Н только по одному следу (например, горизонталь имеет только фронтальный след). Поэтому, зная один след главной линии, проекцию главной линии проводят по заранее известному направлению. Это направление для горизонтали видно из рис. 104, а, где показана плоскость общего положения и горизонталь, лежащая на ней. Из рисунка видно, что горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.

Таким образом, чтобы на комплексном чертеже плоскости Р провести в этой плоскости какую-либо горизонталь, нужно наметить на следе Р_v плоскости точку v’ (рис. 104, б) и считать ее фронтальной проекцией фронтального следа горизонтали. Затем через точку v’ параллельно оси х проводят прямую, которая будет фронтальной проекцией горизонтали.

Опустив перпендикуляр из точки v’ на ось x , получают точку v, которая будет горизонтальной проекцией фронтального следа горизонтали. Прямая, проведенная из точки v параллельно следу P_H плоскости, представляет собой горизонтальную проекцию искомой горизонтали. Построение проекции фронтали показано на рис. 104, в и г.

11 с редко требуется провести горизонталь и фронталь на проецирующих плоскостях. Рассмотрим, например, построение горизонтали на фронтально-проецирующей плоскости (рис. 105). На следе плоскости Р_v намечаем фронтальную проекцию фронтального следа горизонтали и на оси находим его горизонтальную проекцию v (рис. 105, а). Затем через точку проводим параллельно Р_н горизонтальную проекцию горизонтали; фронтальная проекция горизонтали совпадает с точкой v’.

Если плоскость задана не следами, а пересекающимися или параллельными прямыми, то построение проекций горизонтали или фронтали, расположенных в этой плоскости, выполняется следующим образом.

Пусть плоскость задана двумя параллельными прямыми AВ и СD (рис. 105, 6). Для построения горизонтали, лежащей в этой плоскости, проводим параллельно оси х фронтальную проекцию горизонтали и отмечаем точки е’и f’ пересечения фронтальной проекции горизонтали с фронтальными проекциями параллельных прямых, которыми задана плоскость. Через точки е’и f’ проводим вертикальные линии связи до пересечения с ab и cd в точках е и f. Точки е и f соединяем прямой линией, которая и будет горизонтальной проекцией горизонтали.

Если требуется найти следы плоскости, заданной пересекающимися или параллельными прямыми, надо найти следы этих прямых и через полученные точки провести искомые следы плоскости.

Рассмотрим комплексный чертеж параллелограмма ABCD (рис. 106, a),который задает некоторую плоскость X. Отрезок DC расположен в плоскости H, следовательно, его горизонтальная проекция dc является горизонтальным следом плоскости (точнее — горизонтальной проекцией горизонтального следа плоскости).

Чтобы найти фронтальный след этой плоскости, необходимо продолжить горизонтальную проекцию dc прямой DC до пересечения с осью х в точке Р_х, через которую должен пройти искомый фронтальный след плоскости.

Второй точкой v’, через которую пройдет искомый фронтальный след плоскости, является фронтальный след прямой АВ (фронтальная проекция фронтального следа). Фронтальную проекцию фронтального следа прямой АВ находим, продолжая горизонтальную проекцию ab прямой АВ до пересечения с осью х в точке v, которая будет горизонтальной проекцией искомого фронтального следа прямой АВ. Фронтальная проекция фронтального следа этой прямой находится на перпендикуляре, восставленном из точки v к оси х, в точке v’ его пересечения с продолжением фронтальной проекции а’в’ прямой АB. Соединив точки P_x с v’, находим фронтальный след P_v плоскости.

Пример решения подобной задачи приведен на рис 106, б.

Часто на комплексных чертежах приходится решать такую задачу: по одной из заданных проекций точки, расположенной на заданной плоскости, определить две другие проекции точки. Ход решения задачи следующий.

Через заданную проекцию точки, например фронтальную проекцию n’ точки N, расположенной на плоскости треугольника АВС (рис. 107), проводим одноименную проекцию вспомогательной прямой любого направления, например m’к’.

Горизонталью плоскости называется прямая, принадлежащая этой плоскости и параллельная горизонтальной плоскости проекций Н.

Строим другую проекцию mк вспомогательной прямой. Для этого проводим вертикальные линии связи через точки m’ и к’ до пересечения с линиями ас и вс. Из точки n’ проводим линию связи до пересечения с проекцией mк в искомой точке n.

Профильную проекцию n» находим по общим правилам проецирования.

В качестве вспомогательной прямой для упрощения построения чаще используются горизонталь или фронталь.

Чтобы найти какую-либо точку на плоскости Р, например точку А (рис. 108, а и б) надо найти ее проекции а’и а, которые располагаются на одноименных проекциях горизонтали, проходящей через эту точку. Через точку А проведена горизонталь Av’ .

Проводим проекции горизонтали: фронтальную — через v’ параллельно оси х, горизонтальную — через v параллельно следу Р_н плоскости Р. На фронтальной проекции горизонтали намечаем фронтальную проекцию а’ искомой точки и, проводя вертикальную линию связи, определяем горизонтальную проекцию а точки А.

Если точка лежит на проецирующей плоскости, то построение ее проекций упрощается. В этом случае одна из проекций точки всегда расположена на следу плоскости (точнее, на его проекции). Например, горизонтальная проекция а точки А, расположенной на горизонтально-проецирующей плоскости Р, находится на горизонтальной проекции горизонтального следа плоскости (рис. 108, в и г)

При заданной фронтальной проекции a’ точки А, лежащей на горизонтально-проецирующей плоскости , найти вторую проекцию этой точки (горизонтальную) можно без вспомогательной прямой, посредством проведения линии связи через а’ до пересечения со следом Р_Н.

Если точка расположена на фронтально-проецирующей плоскости Р (рис. 108, д и е), то ее фронтальная проекция а’ находится на фронтальном следе Х_v плоскости Р.

ПРОЕКЦИИ ПЛОСКИХ ФИГУР

Зная построение проекций прямых и точек, расположенных на плоскости, можно построить проекции любой плоской фигуры, например, прямоугольника, треугольника, круга.

Как известно, каждая плоская фигура ограничена отрезками прямых или кривых линий, которые могут быть построены по точкам.

Проекции фигуры, ограниченной прямыми линиями (треугольника и многоугольника), строят по точкам (вершинам). Затем одноименные проекции вершин соединяют прямыми линиями и получают проекции фигур.

Проекции круга или другой криволинейной фигуры строят при помощи нескольких точек, которые берут равномерно по контуру фигуры. Одноименные проекции точек соединяют плавной кривой по лекалу.

Проекции плоской фигуры строят различными способами в зависимости от положения фигуры относительно плоскостей проекций и Наиболее просто построить проекции фигуры, расположенной параллельно плоскостям Н и V; сложнее — при расположении фигуры на проецирующей плоскости или на плоскости общего положения.

Рассмотрим несколько примеров.

Если треугольник АВС расположен на плоскости, параллельной плоскости H (рис. 109, a), то горизонтальная проекция этого треугольника будет его действительным видом, а фронтальная проекция — отрезком прямой, параллельным оси х. Комплексный чертеж треугольника АВС показан на рис. 109, 6. Такой треугольник можно видеть на изображении резьбового резца (рис. 109, в),передняя грань которого треугольная.

Трапеция ABCD расположена на фронтально-проецирующей плоскости (рис. 110, а). Фронтальная проекция трапеции представляет собой отрезок прямой линии, а горизонтальная — трапецию (рис. 110, б)

Задняя грань отрезного резца (рис. 110, в) имеет форму трапеции.

Рассматривая плоскость, параллельную горизонтальной, фронтальной или профильной плоскости проекций (плоскость уровня), можно заметить, что любая фигура, лежащая в этой плоскости, имеет одну из проекций, представляющую собой действительный вид этой фигуры; вторая и третья проекции фигуры совпадают со следами этой плоскости.

Рассматривая проецирующую плоскость, заметим, что любая точка, отрезок прямой или кривой линии, а также фигуры, расположенные на проецирующей плоскости, имеют одну проекцию, расположенную на следе этой плоскости. Например, если круг лежит на фронтально-проецирующей плоскости Р (рис. 111), то фронтальная проекция круга совпадает с фронтальным следом Pv плоскости Р. Две другие проекции круга искажены и представляют собой эллипсы. Большие оси эллипсов равны проекциям диаметра круга 37. Малые оси эллипсов равны проекциям диаметра круга 15, перпендикулярного диаметру 37.

На рис. 111,6 показано колено трубы с двумя фланцами. Горизонтальная проекция контура нижнего фланца, который расположен в горизонтальной плоскости, будет действительным видом окружности. Горизонтальная проекция контура верхнего фланца изобразится в виде эллипса.

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ

Две плоскости могут быть взаимно параллельными или пересекающимися.

Из стереометрии известно, что если две параллельные плоскости пересекают какую-либо третью плоскость, то линии пересечения этих плоскостей параллельны между собой. Исходя из этого положения, можно сделать вывод, что одноименные следы двух параллельных плоскостей Р и Q также параллельны между собой.

Если даны две профильно-проецирующие плоскости Р и К (рис. 112, а), то параллельность их фронтальных и горизонтальных следов на комплексном чертеже в системе V и Н недостаточна для того, чтобы определить, параллельны эти плоскости или нет. Для этого необходимо построить их профильные следы в системе V, Н и W (рис. 112, б). Плоскости Р и K будут параллельны только в том случае, если параллельны их профильные следы P_w и K_w.

Одноименные следы пересекающихся плоскостей Р и Q (рис. 112, в) пересекаются в точках V и H, которые принадлежат обеим плоскостям, т. е. линии их пересечения. Так как эти точки расположены на плоскостях проекций, то, следовательно, они являются также следами линии пересечения плоскостей. Чтобы на комплексном чертеже построить проекции линии пересечения двух плоскостей Р и Q, заданных следами P_v, Р_н и Q_v,Q_h, необходимо отметить точки пересечения одноименных следов плоскостей, т. е. точки v’ и h (рис. 112, г); точка v’ — фронтальная проекция фронтального следа искомой линии пересечения плоскостей Р и Q, h — горизонтальная проекция горизонтального следа этой же прямой. Опуская перпендикуляры из точек v’ и h на ось х, находим точки v и h’. Соединив прямыми одноименные проекции следов, т. е. точки v’ и h’, v и h’ получим проекции линии пересечения плоскостей Р и Q.

ПРЯМАЯ, ПРИНАДЛЕЖАЩАЯ ПЛОСКОСТИ

Для этого фронтальную проекцию отрезка m’n’ продолжаем до пересечения с отрезками a’b’ и c’d’ (проекциями сторон треугольника АВС), получаем точки (рис. 113, б).

Из точек е’к’ проводим линии связи на горизонтальную проекцию до пересечения с отрезками ab и ca , получаем точки еk. Продолжим горизонтальную проекцию mn отрезка прямой MN до пересечения с проекциями сторон bа и са, если точки пересечения совпадут с ранее полученными точками e и k то прямая MN принадлежит плоскости треугольника.

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ

Если прямая АВ пересекается с плоскостью Р, то на комплексном чертеже точка их пересечения определяется следующим образом.

Через прямую А В проводят любую вспомогательную плоскость Q. Для упрощения построений плоскость Q обычно берется проецирующей (рис. 114, a). В данном случае проведена вспомогательная горизонтально-проецирующая плоскость Q. Через горизонтальную проекцию аb прямой АВ проводят горизонтальный след Q_H плоскости Q и продолжают его до пересечения с осью x в точке Q_x . Из точки Q_x к оси х восставляют перпендикуляр Q_xQ_y , который будет фронтальным следом Q_v вспомогательной плоскости Q.

Вспомогательная плоскость Q пересекает данную плоскость Р по прямой VH, следы которой лежат на пересечении следов плоскостей Р и Q. Заметив точки пересечения следов P_v и Q_v — точку v’ и следов Q_н и P_H — точку h,опускают из этих точек на ось х перпендикуляры, основания которых — точки v’ и h’ — будут вторыми проекциями следов прямой VH. Соединяя точки v’и h’, v и h, получают фронтальную и горизонтальную проекции линии пересечения плоскостей.

Точка пересечения М заданной прямой AB и найденной прямой VH и будет искомой точкой пересечения прямой АВ с плоскостью Р. Фронтальная проекция m’ этой точки расположена на пересечении проекций a’b’ и v’h’. Горизонтальную проекцию m точки М находят, проводя вертикальную линию связи из точки m’ до пересечения с ab.

Если плоскость задана не следами, а плоской фигурой, например, треугольником (рис. 114, 6), то точку пересечения прямой MN с плоскостью треугольника АВС находят следующим образом.

Через прямую МN проводят вспомогательную фронтально-проецирующую плоскость . Для этого через точки m’ и n’ проводят фронтальный след плоскости Р_у продолжают его до оси x и из точки пересечения следа плоскости Р_у с осью х опускают перпендикуляр Р_н, который будет горизонтальным следом плоскости Р.

Затем находят линию ED пересечения плоскости Р с плоскостью данного треугольника ABC. Фронтальная проекция e’d’ линии ED совпадает с m’n’. Горизонтальную проекцию ed находят, проводя вертикальные линии связи из точек е’и d’ до встречи с проекциями ab и ас сторон треугольника АВС. Точки e и d соединяют прямой. На пересечении горизонтальной проекции ed линии ED с горизонтальной проекцией прямой MN находят горизонтальную проекцию k искомой точки К. Проведя из точки k вертикальную линяю связи, на ходят фронтальную проекцию k’ Точка К — искомая точка пересечения прямой МК с плоскостью треугольника АВС.

В частном случае прямая может быть перпендикулярна плоскости Р.Из условия перпендикулярности прямой к плоскости следует, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим на этой плоскости (в частности, этими прямыми могут быть следы плоскости). Тогда проекции прямой АВ будут перпендикулярны одноименным следам этой плоскости (рис 115, а) Фронтальная проекция а’b’ перпендикулярна фронтальному следу Р_у, а горизонтальная проекция ab перпендикулярна горизонтальному следу Р_н плоскости Р.

Если плоскость задана параллельными или пересекающимися прямыми, то проекции прямой, перпендикулярной этой плоскости, будут перпендикулярны горизонтальной проекции горизонтали и фронтальной проекции фронтали, лежащих на плоскости.

Таким образом, если, например, на плоскость, заданную треугольником АВС необходимо опустить перпендикуляр, то построение выполняется следующим образом (рис. 115, б).

На плоскости проводят горизонталь СЕ и фронталь FA. Затем из заданных проекций d и d’ точки D опускают перпендикуляры соответственно на ce и f’a’. Прямая, проведенная из точки D будет перпендикулярна плоскости треугольника АВС.

ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ

Задачи на построение линии пересечения плоскостей, заданных пересекающимися прямыми, можно решать подобно задаче на пересечение плоскости с прямыми линиями. На рис. 116 показано построение линии пересечения плоскостей, заданных треугольниками АВС и DEF. Прямая MN построена по найденным точкам пересечения сторон DE и EF треугольника DEF с плоскостью треугольника АВС.

Например, чтобы найти точку M, через прямую DF проводят фронтально-проецирующую плоскость Р, которая пересекается с плоскостью треугольника АВС по прямой 12. Через полученные точки 1′ и 2′ проводят вертикальные линии связи до пересечения их с горизонтальными проекциями ав и ас сторон треугольника АВС в точках 1 и 2. На пересечении горизонтальных проекций df и 12 получают горизонтальную проекцию m искомой точки М, которая будет точкой пересечения прямой DF с плоскостью АВС. Затем находят фронтальную проекцию m’ точки M. Точку N пересечения прямой EF с плоскостью АВС находят так же, как и точку М.

Соединив попарно точки m’ и n’, m и n, получают проекции линий пересечения MN плоскостей АВС и DEF.

🎦 Видео

Задача 1.1. Прямая и плоскость. Построить комплексный чертеж треугольника АВС и прямой МN.Скачать

Построение параллельной плоскости на расстояние 30 мм.Скачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Параллельность прямой к плоскостиСкачать

Построение недостающей проекции отрезка прямой линии, лежащей в заданной плоскостиСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Построение недостающих проекций, следы плоской фигурыСкачать

Следы плоскостиСкачать

Линия пересечения плоскостейСкачать

Горизонталь в плоскостиСкачать

Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Лекция 4. ПлоскостьСкачать

Определение кратчайшей расстоянии от точки до плоскостиСкачать

Точка встречи прямой с плоскостьюСкачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Построение параллельной плоскости на расстояние 40 мм. Плоскость задана со следами.Скачать