Построение окружности в изометрии эллипс (6 видео)

Построение окружности в изометрии эллипс

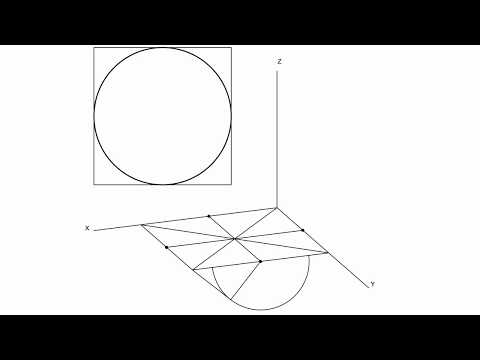
Контрольные задания по теме: эпюр № 6

Для наглядного изображения предметов (изделий или их составных частей) рекомендуется применять аксонометрические проекции, выбирая в каждом отдельном случае наиболее подходящую из них.

Сущность метода аксонометрического проецирования заключается в том, что заданный предмет вместе с координатной системой, к которой он отнесен в пространстве, параллельным пучком лучей проецируется на некоторую плоскость. Направление проецирования на аксонометрическую плоскость не совпадает ни с одной из координатных осей и не параллельно ни одной из координатных плоскостей.

Все виды аксонометрических проекций характеризуются двумя параметрами: направлением аксонометрических осей и коэффициентами искажения по этим осям. Под коэффициентом искажения понимается отношение величины изображения в аксонометрической проекции к величине изображения в ортогональной проекции.

В зависимости от соотношения коэффициентов искажения аксонометрические проекции подразделяются на:

— изометрические, когда все три коэффициента искажения одинаковы (k_x=k_y=k_z);

— диметрические, когда коэффициенты искажения одинаковы по двум осям, а третий не равен им (k_x= k_z ≠k_y);

— триметрические, когда все три коэффициенты искажения не равны между собой (k_x≠k_y≠k_z).

В зависимости от направления проецирующих лучей аксонометрические проекции подразделяются на прямоугольные и косоугольные. Если проецирующие лучи перпендикулярны аксонометрической плоскости проекций, то такая проекция называется прямоугольной. К прямоугольным аксонометрическим проекциям относятся изометрическая и диметрическая. Если проецирующие лучи направлены под углом к аксонометрической плоскости проекций, то такая проекция называется косоугольной. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая, горизонтальная изометрическая и фронтальная диметрическая проекции.

В прямоугольной изометрии углы между осями равны 120°. Действительный коэффициент искажения по аксонометрическим осям равен 0,82, но на практике для удобства построения показатель принимают равным 1. Вследствие этого аксонометрическое изображение получается увеличенным в 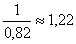раза.

Изометрические оси изображены на рисунке 57.

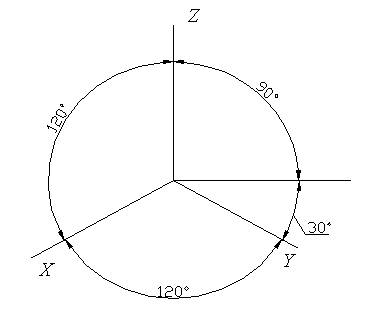
Рисунок 57

Построение изометрических осей можно выполнить при помощи циркуля (рисунок 58). Для этого сначала проводят горизонтальную линию и перпендикулярно к ней проводят ось Z. Из точки пересечения оси Z с горизонтальной линией (точка О) проводят вспомогательную окружность произвольным радиусом, которая пересекает ось Z в точке А. Из точки А этим же радиусом проводят вторую окружность до пересечения с первой в точках В и С. Полученную точку В соединяют с точкой О — получают направление оси Х. Таким же образом соединяют точку С с точкой О — получают направление оси Y.

Рисунок 58

Построение изометрической проекции шестиугольника представлено на рисунке 59. Для этого необходимо отложить по оси X радиус описанной окружности шестиугольника в обе стороны относительно начала координат. Затем, по оси Y отложить величину размера под ключ, из полученных точек провести линии параллельно оси X и отложить по ним величину стороны шестиугольника.

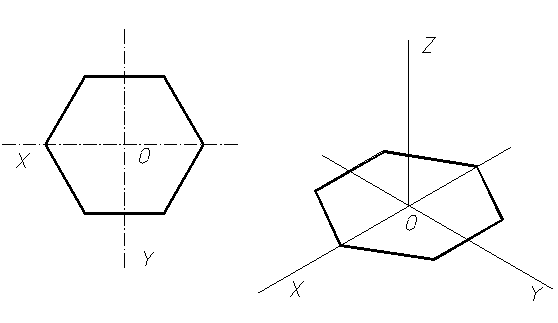
Рисунок 59

Построение окружности в прямоугольной изометрической проекции

Наиболее сложной плоской фигурой для вычерчивания в аксонометрии является окружность. Как известно, окружность в изометрии проецируется в эллипс, но построение эллипса довольно сложно, поэтому ГОСТ 2.317-69 рекомендует вместо эллипсов применять овалы. Существует несколько способов построения изометрических овалов. Рассмотрим один из наиболее распространенных.

Размер большой оси эллипса 1,22d, малой 0,7d, где d — диаметр той окружности, изометрия которой строится. На рисунке 60 показан графический способ определения большой и малой осей изометрического эллипса. Для определения малой оси эллипса соединяют точки С и D. Из точек С и D, как из центров, проводят дуги радиусов, равных СD, до взаимного их пересечения. Отрезок АВ — большая ось эллипса.

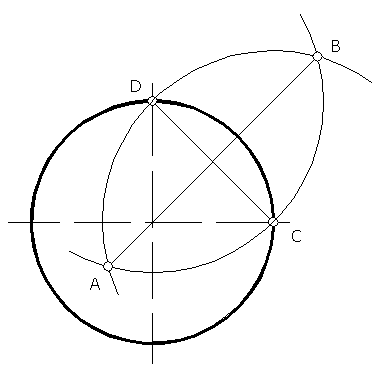
Рисунок 60

Установив направление большой и малой осей овала в зависимости от того, какой координатной плоскости принадлежит окружность, по размерам большой и малой оси проводят две концентрические окружности, в пересечении которых с осями намечают точки О₁, О₂, О₃, О₄, являющиеся центрами дуг овала (рисунок 61).

Для определения точек сопряжения проводят линии центров, соединяя О₁, О₂, О₃, О₄. из полученных центров О₁, О₂, О₃, О₄ проводят дуги радиусами R и R₁. размеры радиусов видны на чертеже.

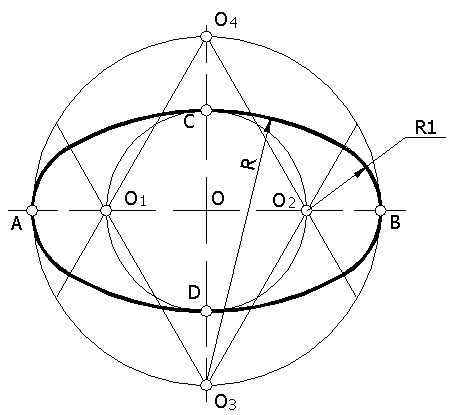
Рисунок 61

Направление осей эллипса или овала зависит от положения проецируемой окружности. Существует следующее правило: большая ось эллипса всегда перпендикулярна к той аксонометрической оси, которая на данную плоскость проецируется в точку, а малая ось совпадает с направлением этой оси (рисунок 62).

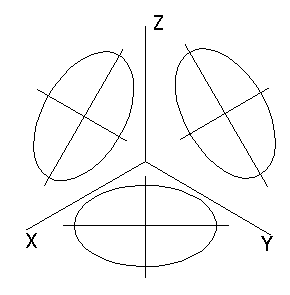
Рисунок 62

Штриховка и изометрической проекции

Линии штриховки сечений в изометрической проекции, согласно ГОСТ 2.317-69, должны иметь направление, параллельное или только большим диагоналям квадрата, или только малым.

Прямоугольной диметрией называется аксонометрическая проекция с равными показателями искажения по двум осям X и Z, а по оси Y показатель искажения в два раза меньше.

По ГОСТ 2.317-69 применяют в прямоугольной диметрии ось Z, расположенную вертикально, ось Х наклонную под углом 7°, а ось Y-под углом 41° к линии горизонта. Показатели искажения по осям X и Z равны 0,94, а по оси Y-0,47. Обычно применяют приведенные коэффициенты k_x=k_z=1, k_y=0,5, т.е. по осям X и Z или по направлениям им параллельным, откладывают действительные размеры, а по оси Y размеры уменьшают в два раза.

Для построения осей диметрии пользуются способом, указанным на рисунке 63, который заключается в следующем:

На горизонтальной прямой, проходящей через точку О, откладывают в обе стороны восемь равных произвольных отрезков. Из конечных точек этих отрезков вниз по вертикали откладывают слева один такой же отрезок, а справа – семь. Полученные точки соединяют с точкой О и получают направление аксонометрических осей X и Y в прямоугольной диметрии.

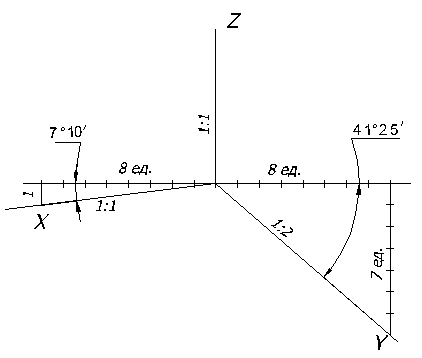
Рисунок 63

Построение диметрической проекции шестиугольника

Рассмотрим построение в диметрии правильного шестиугольника, расположенного в плоскости П₁ (рисунок 64).

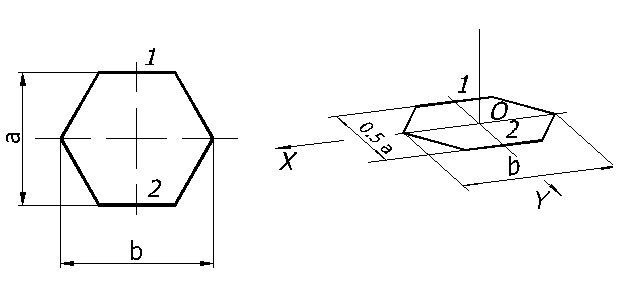
Рисунок 64

На оси Х откладываем отрезок равный величине b, чтобы его середина находилась в точке О, а по оси Y – отрезок а, размер которого уменьшен вдвое. Через полученные точки 1 и 2 проводим прямые параллельно оси ОХ, на которых откладываем отрезки равные стороне шестиугольника в натуральную величину с серединой в точках 1 и 2. Полученные вершины соединяем. На рисунке 65а изображен в диметрии шестиугольник, расположенный параллельно фронтальной плоскости, а на рисунке 66б -параллельно профильной плоскости проекции.

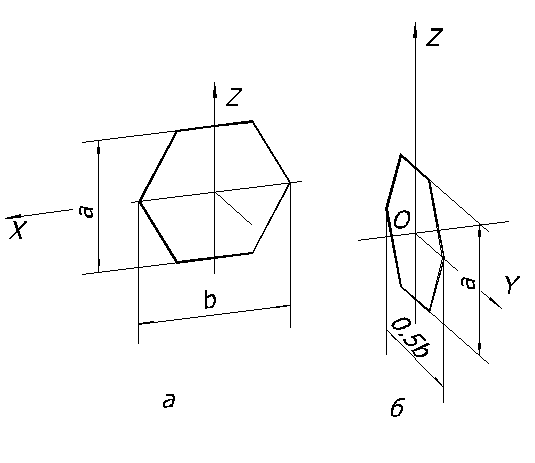
Рисунок 65

Построение окружности в диметрии

В прямоугольной диметрии все окружности изображаются эллипсами,

Длина большой оси для всех эллипсов одинакова и равна 1,06d. Величина малой оси различна: для фронтальной плоскости равна 0,95d , для горизонтальной и профильной плоскостей – 0,35 d.

На практике эллипс заменяется четырехцентровым овалом. Рассмотрим построение овала, заменяющего проекцию окружности, лежащей в горизонтальной и профильной плоскостях (рисунок 66).

Через точку О – начало аксонометрических осей, проводим две взаимно перпендикулярные прямые и откладываем на горизонтальной линии величину большой оси АВ=1,06d , а на вертикальной линии величину малой оси СD=0,35d. Вверх и вниз от О по вертикали откладываем отрезки ОО₁ и ОО₂, равные по величине 1,06d. Точки О₁ и О₂ являются центром больших дуг овала. Для определения еще двух центров (О₃ и О₄) откладываем на горизонтальной прямой от точек А и В отрезки АО₃ и ВО₄, равные ¼ величины малой оси эллипса, то есть d.

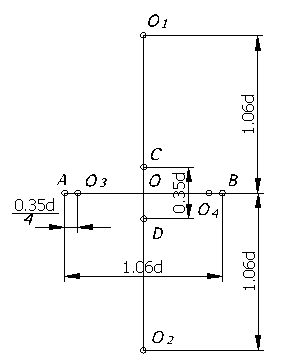
Рисунок 66

Затем, из точек О1 и О2 проводим дуги, радиус которых равен расстоянию до точек С и D, а из точек О3 и О4 – радиусом до точек А и В (рисунок 67).

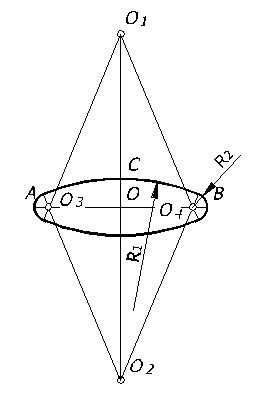
Рисунок 67

Построение овала, заменяющего эллипс, от окружности, расположенной в плоскости П₂, рассмотрим на рисунке 68. Проводим оси диметрии: Х, Y, Z. Малая ось эллипса совпадает с направлением оси Y, а большая перпендикулярна к ней. На осях Х и Z от начала откладываем величину радиуса окружности и получаем точки M, N, K, L, являющиеся точками сопряжения дуг овала. Из точек M и N проводим горизонтальные прямые, которые в пересечении с осью Y и перпендикуляром к ней дают точки О₁, О_2, О_3, О₄ – центры дуг овала (рисунок 68).

Из центров О₃ и О₄ описывают дугу радиусом R₂=О₃ М, а из центров О₁ и О₂ — дуги радиусом R₁= О₂ N

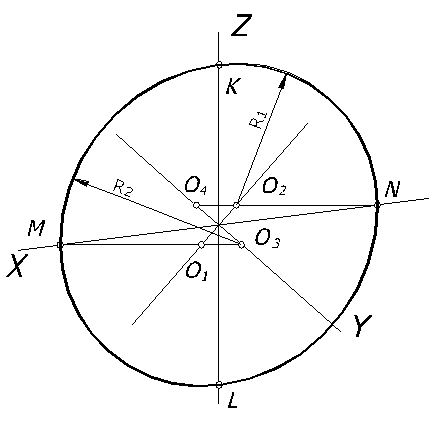
Рисунок 68

Штриховка а прямоугольной диметрии

Линии штриховки разрезов и сечений в аксонометрических проекциях выполняются параллельно одной из диагоналей квадрата, стороны которого расположены в соответствующих плоскостях параллельно аксонометрическим осям (рисунок 69).

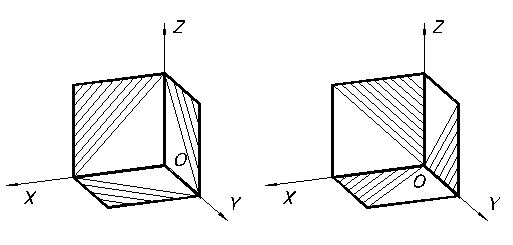
Рисунок 69

Какие виды аксонометрических проекций вы знаете?
Под каким углом расположены оси в изометрии?
Какую фигуру представляет изометрическая проекция окружности?
Как расположена большая ось эллипса для окружности, принадлежащей профильной плоскости проекций?
Какие приняты коэффициенты искажения по осям X, Y, Z для построения диметрической проекции?
Под какими углами расположены оси в диметрии?
Какой фигурой будет являться диметрическая проекция квадрата?
Как построить диметрическую проекцию окружности, расположенной во фронтальной проскости проекций?
Основные правила нанесения штриховки в аксонометрических проекциях.

Тема 12

Наверх

Заключение

Содержание

ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ ОКРУЖНОСТЕЙ
Изображение окружностей в изометрической проекции
Построение изометрических проекций деталей
Понятие о диметрической прямоугольной проекции
Технический рисунок
💡 Видео

Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ ОКРУЖНОСТЕЙ

Окружности в изометрической проекции изображаются эллипсами (рис. 2.55). Их строят с помощью специальных инструментов — лекал. Это процесс трудоемкий. Поэтому в практике выполнения чертежей эллипсы заменяют овалами. Овал — кривая, состоящая из четырех дут окружности.

Рассмотрим построение овала в горизонтальной плоскости, представляющего собой изометрическую проекцию окружности. Строить овал целесообразно путем вписывания его в ромб, который является изометрической проекцией квадрата, описанного вокруг окружности (рис. 2.56, а).

1. Строим оси хиу изометрической проекции (рис. 2.56, б).
2. Строим аксонометрическое изображение квадрата, описанного вокруг окружности. Обратите внимание, что сторона квадрата равна диаметру окружности. Для этого от точки О на осях х и у откладывают отрезки, равные радиусу изображаемой окружности.
3. Через точки, полученные на оси х — 4 и 2, проводим прямые, параллельные оси у, а через точки на оси у — прямые, параллельные оси х. Получим ромб. Отметим точки А и В и проведем большую диагональ ромба, которая пройдет через точку О (рис. 2.56, в).

4. Из вершин тупых углов ромба точек А и В проводим дуги. Их радиус равен расстоянию от вершин тупого угла до точек 4, 3 или /, 2 соответственно (рис. 2.56, г).

Чтобы найти центры меньших дуг овала, через точки А и 4, А и 3 проводят прямые, которые, пересекаясь с большей диагональю ромба, дадут нам точки, которые будут центрами Oj и 0₂ малых дуг овала. Их радиус равен /. Дугами радиуса /?, проводят малые дуги овала (рис. 2.56, д, е).

Аналогичным способом строят овалы, лежащие во фронтальной и профильной плоскостях. Для овала во фронтальной плоскости построение ведут по осям хи^,ав профильной плоскости — по осям zny (рис. 2.57).

На рис. 2.58 показано построение овала без вписывания его в ромб.

Видео:2 2 3 построение изометрии окружностиСкачать

Изображение окружностей в изометрической проекции

Рассмотрим, как в изометрической проекции изображаются окружности. Для этого изобразим куб с вписанными в его грани окружностями (рис. 3.16). Окружности, расположенные соответственно в плоскостях, перпендикулярных осям х, у, z, изображаются в изометрии в виде трех одинаковых эллипсов.

Рис. 3.16. Изометрические проекции окружностей, вписанных в грани куба

Для упрощения работы эллипсы заменяют овалами, очерчиваемыми дугами окружностей, их строят так (рис. 3.17). Вычерчивают ромб, в который должен вписываться овал, изображающий данную окружность в изометрической проекции. Для этого на осях откладывают от точки О в четырех направлениях отрезки, равные радиусу изображаемой окружности (рис. 3.17, а). Через полученные точки a, b, с, d проводят прямые, образующие ромб. Его стороны равны диаметру изображаемой окружности.

Рис. 3.17. Построение овала

Из вершин тупых углов (точек А и В) описывают между точками а и b, а также с и d дуги радиусом R, равным длине прямых Ва или Вb (рис. 3.17, б).

Точки С и Д лежащие на пересечении диагонали ромба с прямыми Ва и Вb, являются центрами малых дуг, сопрягающих большие.

Малые дуги описывают радиусом R, равным отрезку Са (Db).

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Построение изометрических проекций деталей

Рассмотрим построение изометрической проекции детали, два вида которой даны на рис. 3.18, а.

Построение выполняют в следующем порядке. Сначала вычерчивают исходную форму детали – угольник. Затем строят овалы, изображающие дугу (рис. 3.18, б) и окружности (рис. 3.18, в).

Рис. 3.18. Последовательность построения изометрической проекции детали

Для этого на вертикально расположенной плоскости находят точку О, через которую проводят изометрические оси х и z. Таким построением получают ромб, в который вписана половина овала (рис. 3.18, б). Овалы на параллельно расположенных плоскостях строят перенесением центров дуг на отрезок, равный расстоянию между данными плоскостями. Двойными кружочками на рис. 3.18 показаны центры этих дуг.

На тех же осях х и z строят ромб со стороной, равной диаметру окружности d. В ромб вписывают овал (рис. 3.18, в).

Находят центр окружности на горизонтально расположенной грани, проводят изометрические оси, строят ромб, в который вписывают овал (рис. 3.18, г).

Видео:Изображение окружности в перспективе. Эллипс.Скачать

Понятие о диметрической прямоугольной проекции

Расположение осей диметрической проекции и способ их построения приведены на рис. 3.19. Ось z проводят вертикально, ось х – под углом около 7° к горизонтали, а ось у образует с горизонталью угол приблизительно в 41° (рис. 3.19, а). Построить оси можно, пользуясь линейкой и циркулем. Для этого из точки О откладывают по горизонтали вправо и влево по восемь равных делений (рис. 3.19, б). Из крайних точек восставляют перпендикуляры. Высота их равна: для перпендикуляра к оси х – одному делению, для перпендикуляра к оси у – семи делениям. Крайние точки перпендикуляров соединяют с точкой О.

Рис. 3.19. Расположение осей диметрической проекции

При вычерчивании диметрической проекции, как и при построении фронтальной, размеры по оси у сокращают в 2 раза, а по осям х и z откладывают без сокращений.

На рис. 3.20 показана диметрическая проекция куба с вписанными в его грани окружностями. Как видно из этого рисунка, окружности в диметрической проекции изображаются эллипсами.

Рис. 3.20. Диметрические проекции окружностей, вписанных в грани куба

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Технический рисунок

Технический рисунок – это наглядное изображение, выполненное по правилам аксонометрических проекций от руки, на глаз. Им пользуются в тех случаях, когда нужно быстро и наглядно показать на бумаге форму предмета. Обычно в этом возникает необходимость при конструировании, изобретательстве и рационализации, а также при обучении чтению чертежей, когда с помощью технического рисунка нужно пояснить форму детали, представленной на чертеже.

Выполняя технический рисунок, придерживаются правил построения аксонометрических проекций: под теми же углами располагают оси, так же сокращают размеры по осям, соблюдают форму эллипсов и последовательность построения.