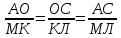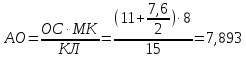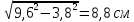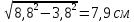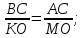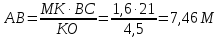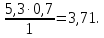Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Описание презентации по отдельным слайдам:
- Применение подобия на практике
- Скачать:
- Предварительный просмотр:
- Введение:
- Обзор литературы
- Что такое подобные треугольники?
- Признаки подобных треугольников.
- Подобие треугольников в жизни.
- 1.4 Что такое геодезия?
- Способы применения подобия
- Измерение дерева
- 1.6.1 Способ Фалеса.
- 1.6.2 С помощью равнобедренного треугольника.
- 1.6.3 Карманная записная книжка.
- 1.6.4 Не приближаясь к дереву.
- 1.6.5 Высотометр.
- 1.6.6 Высотометром, не приближаясь к дереву.
- 1.6.7 Зеркало.
- 1.6.8 По способу Жюля Верна.
- Измерение недоступного расстояния
- 1.7.1 1способ
- 1.7.2 2 способ.
- 1.7.3 3способ.
- Измерения глубины
- Задача древних индусов
- На какой высоте находится шпиль
- Практическая часть
- 2.1 Измерение десяти этажного дома различными способами
- с помощью прямоугольного равнобедренного треугольника
- высотометром
- Способ с помощью зеркала
- Измерение на расстоянии
- Способ с тенью
- При помощи записной книжки
- 2.2 измерение дерева различными способами
- 2.2.1 с помощью записной книжки
- 2.2.2 При помощи высотометра
- 2.2.3 При помощи зеркала
- 2.2.4 С помощью тени
- 2.2.5 С помощью прямоугольного равнобедренного треугольника.
- 2.2.6 измерение на расстоянии
- измерение магазина различными способами
- измерение на расстоянии
- 2.3.2 с помощью прямоугольного равнобедренного треугольника
- 2.3.3 С помощью зеркала
- 2.3.4 высотометром
- 2.3.5 При помощи тени
- 2.3.6 при помощи записной книжки
- измерение школы различными способами
- С помощью зеркала
- 2.4.2 С помощью тени
- Измерение на расстоянии
- С помощью высотометра
- С помощью прямоугольный равнобедренного треугольника
- Частный дом
- Измерение на расстоянии
- При помощи зеркала
- С помощью тени
- Высотометром
- 2.5.5 При помощи записной книжки
- при помощи прямоугольного равнобедренного треугольника
- 2.6 Путь от дома до школы
- 2.6.1 Первый этап
- 2.7 Способ с монетой
- Выводы:
- Список литературы:
- Предварительный просмотр:
- Проектно-исследовательская работа Подобие треугольников в реальной жизни
- Просмотр содержимого документа «11Сушко-t.doc»
- Просмотр содержимого документа «Подобие треугольников в реальной жизни»
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
CLK=> 15/3=5=> MD=3*5=15м. Ответ. » data-title=»Решение ∠L-общий,∠DML= =∠KCL=90° => ΔMLD
CLK=> 15/3=5=> MD=3*5=15м. Ответ. «>
Описание презентации по отдельным слайдам:
Проектная работа на тему: Подобие треугольников и применение их в жизни. Выполнили: ученики 8 класса Чикоткова Арина Ногих Анна Руководитель: учитель математики Фурсенко Н.П. Лизиновка 2016 МКОУ Лизиновская СОШ
Задачи и цели: Узнать где применяется подобие в жизни. Рассмотреть решение задач на местности.
Немного из истории Определение высоты пирамиды по длине ее тени
За шесть веков до нашей эры греческий мудрец Фалес Милетский вычислил высоту египетской пирамиды, измерив длину её тени. Как это было, рассказывается в книге Я.И.Перельмана «Занимательная геометрия». Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени.
На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту.
Применение теории на практике: Определение высоты предмета По шесту. Для измерения нужно взять шест, равный по длине вашему росту. Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было видеть верхушку дерева на одной прямой линии с верхней точкой шеста. Тогда высота дерева будет равна линии, проведенной от вашей головы до основания дерева.
CLK=> 15/3=5=> MD=3*5=15м. Ответ. » title=»Решение ∠L-общий,∠DML= =∠KCL=90° => ΔMLD
CLK=> 15/3=5=> MD=3*5=15м. Ответ. » onclick=»aa_changeSlideByIndex(7, 0, true)» >
Решение ∠L-общий,∠DML= =∠KCL=90° => ΔMLD
CLK=> 15/3=5=> MD=3*5=15м. Ответ: дерево высотой 15 м.
10:1.60=6.25 6.25*1.60=10м Ответ : дерево высотой 10 метров 10м
По луже. Этот способ можно удачно применять после дождя, когда на земле появляется много лужиц. Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершинка предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас
По зеркалу. АВD подобен EFD (по двум углам): ВАD= FED=90°; АDВ = EDF, т.к. угол падения равен углу отражения. В подобных треугольниках сходственные стороны пропорциональны:
12:1=12 12*1.60=19.2м Ответ: дерево высотой 19.2м 19.2м
С какого расстояния уже могут быть различимы объекты. 1. На открытой местности населенные пункты видны с 10-12 км. 2. Многоэтажные строения — 8-10 км. 3. Отдельные одноэтажные (частные) дома – 5-6 км. 4. Окна в домах различимы с 4 км. 5. Трубы печей на крышах — 3 км. 6. Отдельные деревья различимы с 2 км. 7. Люди (в виде точек) – 1,5 – 2 км. 8. Движение рук и ног человека — 700 метров. 9. Переплеты оконных рам – 500 метров. 10. Голова человека – 400 м. 11. Цвет и части одежды — 250-300 м. 12. Листья на деревьях – 200 м. 13. Черты лица и кисти рук – 100 м. 14. Глаза в виде точек – 60-80 м.
Измерение расстояния до недоступной точки. 19.2м 19.2м Палец-0.06м, Расстояние от глаза до пальца-0.5м Расстояние до дерева 160м 19.2:0.06=320 320*0.5=160м
Измерение ширены реки с помощью булавочного прибора
Булавочный прибор для измерений
Также для измерения могут применяться разные инструменты. Экер Экер представляет собой два бруска, расположенных под прямым углом и укреплённых на треножнике. На концах брусков вбиты гвозди так, что прямые, проходящие через них, взаимно перпендикулярны.
Астролябия Устройство: астролябия состоит из двух частей: диска (лимб), разделённого на градусы, и вращающейся вокруг центра линейки (алидады). При измерении угла на местности она наводится на предметы, лежащие на его сторонах. Наведение алидады называется визированием. Для визирования служат диоптры. Это металлические пластинки с прорезами. Диоптров два: один с прорезом в виде узкой щели, другой с широким прорезом, посередине которого натянут волосок. При визировании к узкому прорезу прикладывается глаз наблюдателя, поэтому диоптр с таким прорезом называется глазным. Диоптр с волоском направляется к предмету, лежащему на стороне измеряемого; он называется предметным. В середине алидады прикреплён к ней компас.
Вывод: Подобие треугольников применяется в повседневной жизни довольно часто. Мы выяснили на конкретных примерах, что с помощью подобия можно найти высоту или расстояние до известной или неизвестной нам точки.
Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Применение подобия на практике
Цель работы: узнать больше о подобии треугольников, и каким образом оно применяется на местности. Применить на практике полученные знания.
Задачи:
1. Собрать литературу по данному вопросу.
2. Изготовить необходимое оборудования для измерения на местности..
3. Показать умение проводить измерительные работы на местности: измерить при помощи подобия, объекты, находящиеся по пути в школу несколькими способами и сравнить получившиеся результаты.
4. Вычислить погрешность измерения.
Видео:Подобные треугольникиСкачать

Скачать:
| Вложение | Размер |
|---|---|
| primenenie_podobiya_na_praktike.docx | 824.06 КБ |
| pasport_issledovatelskoy_raboty.docx | 15.37 КБ |
Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Предварительный просмотр:
Муниципальное образовательное учреждение
Средняя общеобразовательная школа
С углубленным изучением отдельных предметов № 89
Применение подобия на практике
Выполнила: Кочанова Лада,
Ученица 8 «Б» класса
Руководитель: Вахрушева Е. В.
Видео:Подобные треугольникиСкачать

Введение:
Геометрические знания и умения, геометрическая культура и развитие являются сегодня профессионально значимыми для многих современных специальностей, для дизайнеров и конструкторов, для рабочих и ученых, и даже для биологов.
Геометрические знания широко применяются в жизни – в быту, на производстве, в науке. При покупке обоев надо знать площадь стен комнаты; при определении расстояния до предмета, наблюдаемого с двух точек зрения, нужно пользоваться известными нам теориями; при изготовлении технических чертежей – выполнять геометрически построения.
На уроках геометрии мы прошли подобие треугольников. Мне эта тема очень понравилась. Недавно я узнала, что с помощью подобия треугольников можно измерять очень большие высоты и недосягаемые расстояния. Мне стало очень интересно, и я решила побольше узнать об этом, попытаться измерить самой некоторые высоты и проанализировать получившиеся результаты.
Цель работы: узнать больше о подобии треугольников, и каким образом оно применяется на местности. Применить на практике полученные знания.
- Собрать литературу по данному вопросу.
- Изготовить необходимое оборудования для измерения на местности..
- Показать умение проводить измерительные работы на местности: измерить при помощи подобия, объекты, находящиеся по пути в школу несколькими способами и сравнить получившиеся результаты.
- Вычислить погрешность измерения.
Объекты и предметы исследования: высота: дом, школы, дерева, магазина, частного дома, а так же путь от дома до школы.
Видео:Подобные треугольники - 8 класс геометрияСкачать

Обзор литературы
Треугольники знакомы нам с детства. Более подробно мы узнали о них в курсе геометрии с 7 класса. Эта геометрическая фигура таит в себе много интересного и загадочного.
С помощью треугольника можно решать много практических задач.
Видео:Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Что такое подобные треугольники?
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Коэффициент подобия равен отношению сходственных сторон подобных треугольников.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.(1)
Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Признаки подобных треугольников.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.(1)
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Подобие треугольников в жизни.
Очень часто для применения подобия на местности, возникает необходимость построения. Такие построения нужны и при строительстве зданий, и при прокладке дорог.
Видео:Ученые установили камеру в гроб. Увиденное в процессе на наблюдения всех шокировало.Скачать

1.4 Что такое геодезия?
При решении хозяйственных и научных вопросов, связанных с поверхностью земли, часто возникают такие задачи:
- Каково расстояние между двумя пунктами;
- Насколько одна точка выше или ниже другой заданной точки;
- Чему равна площадь некоторого участка местности;
- Как направлена (ориентирована) данная линия относительно сторон света и т. д.
Все эти вопросы связаны с изучением поверхности земли в геометрическом отношении, и их решение сводится к определению относительного (взаимного) положения точек этой поверхности.
При организации территории и осуществлении всякого рода строительных работ приходится решать и другие задачи:
- Как на местности построить прямую заданной длинны или круговую кривую данного радиуса.
- Как отбить на местности площадь определенной величины и формы и т. д.
В этом случае наоборот, приходится на поверхности земли (или вблизи нее)
Намечать точки, которые отвечают определенным условиям.
Наука, которая занимается всеми этими вопросами, называется, геодезией. Задачи геодезии теперь можем кратко формулировать так. Геодезия занимается определением относительного (взаимного) положения точек земной поверхности, а также обозначением (маркировкой) на местности точек, отвечающих заданным (проектным) геометрическим условиям.
Результаты геодезических измерений представляют аналитически – каталогами координат и ведомостями высот точек, а также графически – различными чертежами, отображающими по определенному закону местности на плоскости.
Чтобы рационально организовать измерения на поверхности земли и правильно изображать ее на бумаге, нужно иметь достаточно четкое понятие о форме и раздорах Земли.
В большинстве случаев для измерения применяется подобие треугольников.(4)
Видео:Решение задач на тему "Подобные треугольники". 8 классСкачать

Способы применения подобия
Подобие треугольников можно применять для разных целей. Например, для измерения высоты дерева.
Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Измерение дерева
1.6.1 Способ Фалеса.
Самый легкий и самый древний способ – который греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Жрецы и Фараон, собравшиеся у подножья высочайшей пирамиды, озадаченно смотрели на северного пришельца, отгадывающего по тени высоту огромного сооружения. Фалес выбрал день, и час когда его тень ровнялась его росту, тогда и высота пирамиды должна соответствовать ее высоте.
Таким образом, можно измерить и высоту дерева.
Но этот способ не всегда можно применить. Чтоб не дожидаться когда ваша тень станет равна вашему росту можно поступить проще.
Измерить тень дерева и вашу собственную. Во сколько раз тень дерева больше вашей, значит во столько же раз дерево выше вашего роста. Из этого можем составить пропорцию(рис. 1): AB:ED=BC:EF
Это вытекает из геометрического подобия треугольников АВС и DEF.
Но этим способом мы получаем не совсем точные результаты.(2)
1.6.2 С помощью равнобедренного треугольника.
Вполне возможно обойтись при измерении высоты и без тени. Мы можем воспользоваться свойством равнобедренного прямоугольного треугольника. Для этого надо изготовить один простой прибор, его можно изготовить из дощечки и двух булавок (рис. 2).
- На дощечке любой формы намечают три точки – вершины равнобедренного прямоугольного треугольника.
- В них втыкается по булавке.
- К верхней булавке привязывается ниточка с грузиком.
Приближаясь к дереву или отдаляясь от него вы всегда найдете такое место А (рис. 3), из которого, глядя на булавки E и F, увидите, что они покрывают верхушку С дерева: это значит что продолжение гипотенузы E F проходит через точку С. Тогда, очевидно, расстояние ЕВ равно СВ, так как угол Е= .
Следовательно, измерив, расстояние ЕВ и прибавив OB, т. е. возвышение АЕ глаза над землей, получите искомую высоту дерева.(4)
1.6.3 Карманная записная книжка.
Можно измерить высоту дерева с помощью записной книжки, если она снабжена карандашом, всунутым в чехлик или петельку при книжке. Она поможет построить вам в пространстве те два подобных треугольника, из которых получается искомая высота. Книжку надо держать возле глаза так, как показано на (рис. 4).
Она должна находиться в отвесной плоскости, а карандаш выдвигаться над верхним обрезом книжки на столько, чтобы глядя из точки Е, видеть вершину В дерева покрытой кончиком О карандаша. Тогда вследствие подобия треугольников ECB и EFO. Высота ВС определится из пропорции: BC:OF=EC:FE.
К полученному расстоянию ВС нужно прибавить еще длину СD, т. е. – на ровном месте высоту глаза над почвой.(3)
1.6.4 Не приближаясь к дереву.
Бывает так, что нельзя подойти к дереву вплотную. Но в таком случае его высоту измерить вполне возможно. Для этого надо изготовить один простой прибор:
Две планки МО и ЕF соединяются под прямым углом так, чтобы МF ровнялось FO, а FМ составляла половину ЕF. Вот и весь прибор (рис.5).
Чтобы измерить им высоту держат его в руках, направив планку ОF вертикально (для этого на ней имеется отвес – шнурок с грузиком), и становятся последовательно в двух местах (рис. 6):
сначала в точке А, где располагают прибор концом О вверх, а затем в точке А 1 , подальше, где прибор держат концом М вверх. Точка А избирается так, чтобы, глядя из Е на конец О, видеть его на одной прямой с верхушкой дерева. Точку же А1отискивают так, чтобы глядя из Е1 на точку М 1 , видеть ее совпадающей с В. В отыскании этих двух точек А и А 1 заключается все измерение, потому что искомая часть высоты дерева ВС равна расстоянию АА 1 . Равенство вытекает из того, что EС=ВС, а Е 1 С=ВС; значит: Е 1 С-ЕС=ВС.
В этом способе мы не подходим к самому дереву, но можем узнать его высоту.(2)
1.6.5 Высотометр.
Можно измерить высоту дерева с помощью специального прибора – высотометра. Его можно легко изготовить (рис. 7):
- Картонный или деревянный прямоугольник OMNQ.
- На вершину M привязан грузик с ниточкой.
- На краю ОF нанести сантиметровые деления.
Подойдя к дереву держат высотомер так чтобы глядя вдоль края MN видеть на одной линии с ним вершину В дерева (рис. 8). В точке М привешен на нити грузик F. Находим точку Е в которой нить пересекает линию OQ . треугольники МВС и МОЕ подобны, так как оба прямоугольные и имеют равные острые углы МВС и МЕО(с соответственно параллельными сторонами), значит мы в праве написать пропорцию:
ВС:ЕО=МС:МО, отсюда: ВС=МС* .
Так как МС, ЕО и МО можно измерить непосредственно, то легко получить искомую высоту дерева, прибавив длину нижней части СD ствола (высоту прибора над почвой.(2)
1.6.6 Высотометром, не приближаясь к дереву.
Высотометром можно измерять высоту деревьев, к которым нельзя подойти вплотную. Надо направит прибор на вершину В дерева с двух точек А и А 1 (рис. 9).
Пусть в точке А мы определили, что ВС=0.9АС а в точке А 1 – что ВС=0.4А1С. Тогда мы знаем, что , , откуда итак, , или .(2)
1.6.7 Зеркало.
Высоту дерева можно определить при помощи зеркала. На некотором расстоянии от измеряемого дерева на ровной земле в точке С кладут горизонтально зеркальце и отходят от него назад в такую точку D, стоя в которой наблюдатель видит в зеркале верхушку А дерева. Тогда дерево АВ во столько раз выше роста наблюдателя ЕD, во сколько раз расстояние ВС от зеркала до дерева больше расстояния СD от зеркала до наблюдателя.
Способ основан на законе отражения света. Вершина А отражается в точке А1 так, что АВ=А 1 В. (рис. 10).
Из подобия же треугольников ВСА 1 и СЕD следует, что А 1 В: УВ=ВС:СD.
В этой пропорции остается лишь заметитьА 1 В равным ему АВ, чтобы обосновать указанное в задаче соотношение.(2)
1.6.8 По способу Жюля Верна.
Этот способ описан в книге у Жюля Верна в известном романе «Таинственный остром». Там инженер и Герберт измеряют высоту площадки дальнего вида. Я же расскажу этот способ на примере измерения дерева.
Здесь нужен шест, который придется воткнуть в землю отвесно так, чтобы выступающая часть как раз ровнялась росту человека. Место для шеста надо выбирать так, чтобы лежа, (как показано на рис.12). (2)
было видно верхушку дерева на одной прямой линии с верхней точкой шеста. Получим два прямоугольных треугольника. Катетами первого будет являться шест и расстояние от шеста до головы человека лежащего на земле. Катетами второго треугольника будут являться: расстояние от головы человека до дерева и та высота дерева, которую нам нужно определить. Мы можем определить расстояние от головы до шеста и от головы до дерева, так же нам известна высота шеста, следовательно, мы можем составить пропорцию и найти искомую высоту.(2)
Видео:Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

Измерение недоступного расстояния
Так же при помощи подобия можно измерить расстояния от точки до недоступной точки, например находящейся на другом берегу реки.
1.7.1 1способ
С помощью подобия можно измерять и расстояния, которые невозможно измерить. Например, ширину реки.
АВ это ширина реки. Находим точку С на продолжении АВ с помощью прибора (рис. 2). Держим этот прибор так чтобы смотря вдоль двух булавок, вы видели, как обе они покрывают точки В и А. затем намечается прямая СD под прямым углом к СА, с помощью этого же прибора. На прямой СD отмечают точки Е и F, так чтобы СЕ было в несколько раз больше ЕF. Затем в точке М с булавочным прибором намечают направление FG, перпендикулярное к FС. Теперь идя по прямой FG, отыскивают на этой прямой такую точку Н, из которой веха Е кажется покрывающей точку А. Получилось, что FН во столько раз меньше АС во сколько FЕ меньше ЕС.(2)
1.7.2 2 способ. 
Пусть в реке есть остров и на нем дерево это точка С. Нужно узнать на каком расстоянии оно находится
Для выполнения данной работы потребуется астролябия (прибор для измерения углов на местности рис.15), рулетка и вехи.
Вехи устанавливают в точки А и В и с помощью астролябии измеряют угол 1 и угол 2. Рулеткой измеряют расстояние от точки А до В. На плоскости строят треугольник А1В1С1 с углами равными углу 1 и углу 2, этот треугольник будет подобный треугольнику АВС по первому признаку подобия (по двум углам), следовательно можно найти сходственные стороны треугольников на плоскости – измерением, а на местности вычислением.
1.7.3 3способ.
Необходимо измерить на местности расстояние между двумя объектами, разделенными зданием или другим препятствием, не позволяющим непосредственно проложить прямую между этими объектами.
Пуст А и В это объекты между которыми надо найти расстояние (рис. 16)
Выберем точку С из которой видны обе точки А и В. На продолжении отрезка АС за точку С отметим точку D на расстоянии предположим в два раза меньше чем АС. Аналогично на продолжении отрезка ВС за точку С отметим точку Е расстояния от точки С до которой в два раза меньше расстояния ВС. Тогда треугольники подобны по второму признаку( по двум сходственным сторонам и углу между ними). Если коэффициент подобия равен 2, то АВ больше ЕD в два раза.
С помощью подобия треугольников можно измерять не только высоту и расстояния, но и даже глубину водоема.(3)
Видео:ЛАГЕРНЫЕ ДОМА УДОВОЛЬСТВИЙ: что там творили с женщинамиСкачать

Измерения глубины
Задача древних индусов
Над озером тихим,
С полфута размером,
высился лотоса цвет.
И ветер порывом
Отнес его в сторону. Нет
Воле цветка над водой,
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока?
Обозначим искомую глубину СD через х. Тогда по теореме Пифагора легко найти искомую глубину.(4)
Видео:МАТЕМАТИКА И ПОДЪЕМ ЦИВИЛИЗАЦИИ / Рейтинг 8.2 / ДОКУМЕНТАЛЬНОЕ КИНО (2012)Скачать

На какой высоте находится шпиль
Так же, с помощью подобия, можно узнать на какой высоте находится шпиль, расположенный на здании, внутри и вблизи которого измерения затруднительны.
Необходимо установить вертикальный шест на некотором расстоянии от здания, и станем в точу из которой верхушка шпиля зрительно совмещается с верхним концом шеста.
Затем пройдя некоторое расстояние в направлении от здания по прямой, на которой лежит первая точка и проекция А шпиля на горизонтальную плоскость, еще раз проделайте такую же операцию. Пусть высота шеста над уровнем глаза ровна а, расстояние от глаза до шеста в первом положении оказалось равно b, а во втором с. Тогда, измерив расстояние у между точками В и С, в которых мы стояли в первом и во втором случаях, можно сосчитать высоту х шпиля над уровнем глаза. В самом деле обозначим через z расстояние между точками А и В. Из подобия соответствующих треугольников имеем
Откуда bx = az, c = az + ay и cx – bx = ay, т. е.
Коэффициент при у в последнем равенстве можно сделать равным 1, если в первом положении шеста добиться равенства a-b, а во втором – равенства c=2a.(4)
Видео:8 класс, 20 урок, Определение подобных треугольниковСкачать

Практическая часть
Видео:Выживший летчик рассказал, что он увидел в Бермудском треугольникеСкачать

2.1 Измерение десяти этажного дома различными способами
с помощью прямоугольного равнобедренного треугольника
Я взяла прибор, который сама изготовила (рис. 2). Нашла то место, в котором верхушка С дома являлась продолжением гипотенузы ЕF треугольника EFD.
Так как угол Е= то треугольник EFD равнобедренный, а значит треугольник ЕСВ тоже равнобедренный. Я измерила расстояние ЕВ, оно получилось равно 145 шагов, это 3770см и прибавила к нему ОВ=100см. Высота дома получилась равна 3870см=38.7 м
высотометром
Потом я измеряла высотометром (рис.7).
Я встала от него на расстоянии 193 шагов, что равно 5174см. Веревочка с грузиком показывала на 12см, а сторона дощечки равна 16 см
Дл измерения высоты дома измерили:
Расстояние от меня до дома – 5018см
Ширину дощечки – 16см
Показания прибора – 12см
Уровень глаз над землей – 100см
Чтобы найти высоту дома
Высота дома без уровня глаз = 5174 * 12 : 16 = 3764см=37.64м
Высота дома = 3764см = 100см = 3864см = 38.64м
Способ с помощью зеркала
Расстояние от зеркала до меня СD=26*5=130см, а расстояние от меня до дома – СВ=26*120=3120м мой рост равен 158см. можно .
Для измерения высоты дома измеряла:
Расстояние от меня до зеркала – 130см
Расстояние от зеркала до дома – 3120см
Мой рост – 158см
Чтобы найти высоту дома
Высота дома = 3250 * 158 : 130 = 3950см = 39.50м
Измерение на расстоянии
Я решила измерить дом способом номер 4. Поэтому подошла к нему с другой стороны где нельзя было подойти в плотную к нему, из за сугробов и измерила с помощью прибора (рис. 5).
Расстояние от точки А до точки А 1 получилось равным 3856см., значит высота дома равна 3856см=38.56м.
Способ с тенью
Мой рост 158см а моя тень была равна 12 шагам – 312см. Примерно в два раза больше меня. Значит тень дома тоже в два раза больше него. Его тень получилась равна 297 шагов значит 7722см. разделила на два и получилось 3861см. значит высота дома равна 3861см=38.61м.
При помощи записной книжки
Ширина записной книжки равна 10см, длинна карандаша, выступающего вверх равна 12см, а расстояние от меня до дома равно 120 шага значит 3120см.
Для измерения высоты дома я измерила:
Ширину записной книжки – 10см
Расстояние от меня до дома – 3120см
Уровень глаза над землей – 100м
Высота дома без уровня глаза над землей =
Высота без уровня глаза над землей = 3120 * 12 :10=3744см
Высота дома = 3744см + 100см =3844см=38.44м
Относительно среднего арифметического
При помощи высотометра:
При помощи зеркала:
Равнобедренный прямоугольный треугольник:
При помощи записной книжки.
Видео:ПОДОБИЕ ТРЕУГОЛЬНИКОВСкачать

2.2 измерение дерева различными способами
Дальше по дороге в школу мне встретилось высокое дерево я провела его измерения.
2.2.1 с помощью записной книжки
Я достала записную книжку выдвинула карандаш с вершиной Е и встала на то места чтобы глядя из точки О на вершину Е я видела вершину В дерева на одной линии с Е и О
Получились подобные треугольники ВОС и ЕОF. Высоту дерева можем узнать из пропорции: BC:ЕF=ОC:FО.
ЕF=12см. FО=10см., ОС равно 24 шагов значит 624см.
Для измерения высоты дерева я измерила:
Ширину записной книжки – 10см
Расстояние от меня до дерева – 624см
Уровень глаза над землей – 100м
Высота дерева без уровня глаза над землей = 624 * 12 : 10 = 748.8см
Высота дерева = 748.8см +100см = 848.8см = 8.49м
2.2.2 При помощи высотометра
Расстояния на котором я находилась от дерева было равно 32 шагам значит 832см. направив высотометр на вершину дерева веревочка остановилась на 15см, а край дощечки равен 16.
Для измерения высоты дерева я измерила:
Расстояние от меня до дерева – 832см
Ширину дощечки – 16см
Показания прибора – 15см
Уровень глаз над землей – 100см
=832*15:16 = 780см
Высота дерева равна 780см + 100см = 880см = 8.8м
2.2.3 При помощи зеркала
Я наша точку в которую, положив зеркало я видела вершину дерева.
Расстояние от меня до зеркала было равно 7 шагам, значит 182см, а расстояние от зеркала до дерева было равно 37 шагам, значит 962см, мой рост равен 158см.
Для измерения высоты дерева я измерила:
Расстояние от меня до зеркала – 182см
Расстояние от зеркала до дерева – 962см
Мой рост – 158см
Высота дерева = 962 *158 : 182 = 835см = 8.35м
Высота дерева = 835см = 8.35м
2.2.4 С помощью тени
Мой рост 158см, моя тень получилась 312см. примерно в два раза больше, значит и тень дерева в два раза больше его натуральной величины. Тень дерева получилась 65 шагов, значит 1690см. разделим на два и получим 845см. Высота дерева равна 845см = 8.45м .
2.2.5 С помощью прямоугольного равнобедренного треугольника.
Я отошла на расстояние, чтобы продолжение гипотенузы треугольника проходило через верхушку дерева. Расстояние получилось равно 29 шагов, значит 754см.
Высота дерева равна 754см плюс 100см (уровень глаза над землей), равно 854см = 8.54м.
2.2.6 измерение на расстоянии
Так же я использовала и способ номер 4, представив, что не могу подойти к дереву. Я нашла две точки А и А1. Расстояние между ними было равно 33 шага, значит 858см.
Высота ровна 858см = 8.58м.
Относительно среднего арифметического
При помощи высотометра:
При помощи зеркала:
Равнобедренный прямоугольный треугольник:
При помощи записной книжки.
Видео:Подобные треугольникиСкачать

измерение магазина различными способами
измерение на расстоянии
На пути магазин «Айкай». Его я измерила 4 способом.
Взяла прибор который сделала сама (рис. 5). Встала сначала в точку А так чтоб глядя в точку Е Видеть точку О прибора и точку В вершину магазина на одной линии. Затем моя подруга с таким же прибором встала в точку А1 так чтобы глядя в точку Е1 видеть точку М1 прибора и точку В вершину магазина на одной линии. (рис. 15).
Расстояние АА 1 у меня получилось равным 32 шагам, значит 832см. следовательно высота магазина равна 832см = 8.32м
2.3.2 с помощью прямоугольного равнобедренного треугольника
Так же как и в предыдущих случаях с деревом и домом, я встала в ту точку чтобы гипотенуза проходила через вершину магазина, а затем измерила расстояние от себя до здания, которое получилось равным 28 шагам, значит 728см плюс 100см (уровень глаз над землей). Высота магазина получилась равна 828см = 8.28м.
2.3.3 С помощью зеркала
Нашла точку в которую положив зеркало я видела вершину магазина.
Расстояние от меня до зеркала получилось равным 7 шагам, значит 182см, расстояния от зеркала до магазина равно 38 шагов, значит 988см, а мой рост равен 158см.
Для измерения высоты магазина я измерила:
Расстояние от меня до зеркала – 182см
Расстояние от зеркала до магазина – 988см
Мой рост – 158см
Высота магазина = 988 * 158 : 182 = 858см = 8.58м. равна 858см=8.58м.
2.3.4 высотометром
Расстояние, на котором я находилась от магазина, было равно 19 шагам, значит 494см. я совместила верхние углы с вершиной магазина так, чтобы все они лежали на одной прямой. Ниточка с грузиком показывала на 24см, а сторона дощечки равна 16см.
Для измерения высоты магазина я измерила:
Расстояние от меня до магазина – 494см
Ширину дощечки – 16см
Показания прибора – 24см
Уровень глаз над землей – 100см
= 494 * 24 : 16 = 741см.
высота магазина = 741см + 100см = 841см = 8.41м.
2.3.5 При помощи тени
В этот раз моя тень оказалась в два раза меньше меня. Значит и тень магазина в два раза меньше него. Тень ровна 16 шагам, значит 416см. высота магазина ровна 832см = 8.32м.
2.3.6 при помощи записной книжки
Ширина книжки ровна 10см, а выступающая часть карандаша ровна 12см. расстояния на которое я отошла чтобы совместить угол книжки, верхушку карандаша и верхушку магазина ровно 23шагов, значит 598см.
Для измерения высоты магазина я измерила:
Ширину записной книжки – 10см
Расстояние от меня до магазина – 598см
Уровень глаза над землей – 100м
Высота магазина = 717см + 100см = 817см=8.17м.
Относительно среднего арифметического
При помощи высотометра:
При помощи зеркала:
Равнобедренный прямоугольный треугольник:
При помощи записной книжки.
Видео:ПОДОБНЫЕ ТРЕУГОЛЬНИКИ коэффициент подобия 8 классСкачать

измерение школы различными способами
Больше всех мне хотелось узнать какой же высоты наша школа.
С помощью зеркала
Я взяла зеркала и положила его в точку D так чтоб встав в точку С видеть в зеркале вершину А школы.( Рис.16).
СD =144см, ВD=1300см, а мой рост равен 158см.
Для измерения высоты школы я измерила:
Расстояние от меня до зеркала – 144см
Расстояние от зеркала до школы – 1300см
Мой рост – 158см
Высота школы = 1300 * 158 : 144 = 1426см.
Значит высота школы равна 1426см = 14.26м .
2.4.2 С помощью тени
Моя тень была в 2.5 раза выше меня, значит и тень школы во столько же раз выше ее. Тень школы ровна 141 шагу, значит 3666см. школа ровна 1466.4см=14.66м.
Измерение на расстоянии
Используя прибор (рис. 5). Я нашла две точки А и А1. Расстояние между которыми равно 56 шагов, значит 1456см. следовательно, высота школы ровна 1456см = 14.56см.
С помощью высотометра
Расстояние, на которое я отошла от школы равно 38 шагов, значит 988см. ниточка с грузиком оказалась на делении 22см. сторона дощечки равна 16см.
Для измерения высоты школы я измерила:
Расстояние от меня до школы – 988см
Ширину дощечки – 16см
Показания прибора – 22см
Уровень глаз над землей – 100см
=988 * 22 : 16 = 1358.5см
Высота школы = 1358.5см + 100см = 1458.5см = 14.58м.
С помощью прямоугольный равнобедренного треугольника
Я нашла точку стоя в которой продолжение гипотенузы проходит через вершину школы. Измерила расстояние от меня до школы, оно получилось равно 51шагу, значит 1326см.
Высота школы равна 1326см плюс 100см(уровень глаз над землей) равно 1426см = 14.26см.
- При помощи записной книжки
Я отошла на расстояние 44 шагов, значит 1144см. ширина книжки ровна 10см, а длинна карандаша 12см.
Для измерения высоты школы я измерила:
Ширину записной книжки – 10см
Расстояние от меня до школы – 598см
Уровень глаза над землей – 100м
=1144 * 12 :10 = 1372.8см.
.Высота школы = 1372.8см + 100см = 1472.8см = 14.73м.
Относительно среднего арифметического
При помощи высотометра:
При помощи зеркала:
Равнобедренный прямоугольный треугольник:
При помощи записной книжки.
Вывод: по техническому паспорту школы, высота школы равна 14.2 м. По моим расчетам более точные измерения получились при помощи зеркала и равнобедренного треугольника. А среднее арифметическое всех вычислений близко к данным технического паспорта.
Частный дом
Измерение на расстоянии
Используя прибор(рис. 5). Я нашла две точки А и А 1 . Расстояние между которыми равно 26 шагов, значит 676см. следовательно высота школы ровна 676см = 6.76см.
При помощи зеркала
Я взяла зеркало положила его на землю так чтобы видеть вершину дома. Расстояние от меня до зеркала получилось равно 5 шагов, значит 130см, а расстояние от зеркала до дома равно 22шага, значит 572см, мой рост равен 158см.
Для измерения высоты частного дома я измерила:
Расстояние от меня до зеркала – 130см
Расстояние от зеркала до частного дома – 572см
Мой рост – 158см
Высота частного дома = 572 * 158 : 130 = 695см = 6.95м.
С помощью тени
Моя тень в 1.8 раза больше меня, значит и тень дома тоже в 1.8 раза больше него. Его тень равна 47 шагам, значит 1222см.
Разделим на 1.8 и получим 678.8см = 6.79м . это и есть высота дома.
Высотометром
Я отошла на расстояние 21 шага значит на 546см. совместила верхние углы высотомера с вершиной дома и получила показание на шкале 17 см, а край высотомера равен 16см.
Для измерения высоты частного дома я измерила:
Для измерения высоты магазина я измерила:
Расстояние от меня до частного дома – 546см
Ширину дощечки – 16см
Показания прибора – 17см
Уровень глаз над землей – 100см
Высота дома ровна 580см плюс 100см(уровень глаза над землей) равно 680см= 6.8м.
2.5.5 При помощи записной книжки
Ширина записной книжки равна 10см, а карандаш торчащий сверху 12см, я отошла на расстояние 19 шагов , значит 494см.
Для измерения высоты частного дома я измерила:
Ширину записной книжки – 10см
Расстояние от меня до частного дома – 494см
Уровень глаза над землей – 100м
Высота дома = 592см + 100см = 692см = 6.92м
при помощи прямоугольного равнобедренного треугольника
Расстояние на которое мне пришлось отойти от дома чтобы продолжение гипотенузы проходило через вершину дома равнялось 22 шагам, значит 572см.
Высота дома равна 572см плюс 100см (высота глаза над землей) равно 672см= 6.72м
Высота частного дома:
Относительно среднего арифметического
При помощи высотометра:
При помощи зеркала:
Равнобедренный прямоугольный треугольник:
При помощи записной книжки.
При помощи зеркала
Две палочки перпендикулярные друг к другу
2.6 Путь от дома до школы
Последним моим измерением был путь от дома до школы. Его я измерила в три этапа (рис. 18):
- От дома до центра детского творчества
- От центра детского творчества до айкая
- От айкая до школы
2.6.1 Первый этап
Поставили два колышка: один около моего подъезда, а другой около ЦДТ. Прошла вдоль дома, который мешает провести прямую между этими точками. Встала в то место, где были видны оба этих колышка, и поставила там веху. Затем после точки пересечения – вехи я отложила расстояния в четыре раза меньше чем от вехи до дт, и от вехи до моего подъезда. Зрительно соединила эти две точки и получила прямую равную 197 шагов, значит 5122см,в четыре раза меньше моего расстояния. Значит расстояние равно 5122*4= 20488см=204.88м.
2.6.2 Второй этап
На этом этапе прямую между магазином и ЦДТ мешает провести куча деревьев. Я так же поставила два колышка: один у ЦДТ, а другой у магазина. Прошла в ту точку, чтобы было видно оба голышка. Поставила там веху. Затем отложила на обеих прямых, как и в первом этапе расстояния в четыре раза меньше. Соединила получившиеся точки и измерила расстояния между ними. Оно получилось равным 130 шагам, значит 2678см. Значит искомое расстояние равно 2678*4= 10712см=107.12м.
2.6.3 Третий этап
На этом этапе я проделала те же действия что и на двух предыдущих и получила длину пути равную 13505см=135.05м
Весь пут = 20488см + 10712см + 13505см = 44705см=447.05м
2.7 Способ с монетой
Читая литературу, я познакомилась вот с такой задачей:
Дерево высотой 15 м закрывается монетой диаметром 2 см, если ее держать на расстоянии 70 см от глаз. Найдите расстояние от дерева до наблюдателя.
Решить ее довольно просто.
2см : 1500см = 70см : НО
НО= = 52500см = 525м
Меня эта задача очень заинтересовала. Я решила попробовать измерить с помощью монеты высоту своего дома.
Если встать в то место когда монетка будет закрывать высоту дома, и смотреть через середину ее диаметра.
Треугольник МНЕ подобен треугольнику МВА по двум углам.
Высота моего роста ровна 158см
А длина от меня до дома 7280см
Получим прямоугольный треугольник ТМА. И с помощью теоремы Пифагора найдем гипотенузу. Гипотенуза, получилась, равна 72.82м.
Тогда можно узнать отношение треугольников МСЕ и МОА.
МС=5см , СЕ=1.4см по теореме Пифагора МЕ=5.2см
ОА = 1960.5см = 19.61м
Так как ОА = ОВ то АВ = 2ОА
Этот способ еще нужно проверить и доработать, но с помощью него так же можно выяснить высоту дома.
Выводы:
Подобие треугольников в жизни незаменимо. Подобие применяется от школьной тетради вплоть до вселенной. Я узнала много нового об этом свойстве треугольников и применила его на местности. Знания, полученные в ходе исследовательской работы, останутся в моей памяти надолго.
Я исследовала различные способы измерения на местности и применила их на практике. Также изготовила приборы для этих измерений.
Определив погрешность моих измерений, я поняла, что измерения неточные, но возможно это зависит от погодных условий, так как измерения проводятся на ровной поверхности, но на улице много сугробов и поэтому ровной поверхности достичь не удалось.
Список литературы:
- Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняков, И. И. Юдина. Геометрия. М. Просвещение. 2005г. 138с.
- Я. И. Перельман. Занимательная геометрия. Домодедово. 1994г. 11-27с.
- . И Баврин. Большой справочник школьника. Математика. М. дрофа. 2006г. 435с.
- http://festival.1september.ru/articles/418615/
Предварительный просмотр:
Применение подобия на практике
Фамилия Имя Отчество автора
Кочанова Лада Олеговна
Полное наименование образовательного учреждения
Муниципальное общеобразовательное учреждение, средняя общеобразовательная школа №89 «с углубленным изучением отдельных предметов»
Класс, в котором учится Автор
Почтовый адрес учреждения с индексом
426006, г.Ижевск, ул. Заречное шоссе, дом 37.
Телефон учреждения с кодом
548990 (секретарь), 548989 (директор)
Электронные адреса для ведения переписки
Фамилия Имя Отчество руководителя работы
Вахрушева Елена Вячеславовна
При проектировании высотных зданий, архитектурных сооружений учитывается высота построения. Нельзя ли на начальной стадии проектирования применить метод подобия, для измерения или определения высоты будущего высотного здания или архитектурного сооружения
Объект и предмет исследования
Объект — высота объектов находящихся по дороге в школу, длинна пути от дома до школы.
Предмет исследования – метод подобия для нахождения высоты объекта
Возможность применения данной методики при проектировании последующих зданий и архитектурных сооружений
При измерении высоты при помощи подобия выявлена погрешность измерения примерно 20 см, при строительстве эта погрешность сыграла бы большую роль.
Практическая значимость работы
Данная работа дает расширенный материал для изучения темы «подобие», а так же дает возможность учащимся создания нового проекта по архитектуре
На уроках геометрии мы изучили тему «Подобие треугольников», а в романе Жюля Верна «Таинственный остров» инженер и Герберт измеряют высоту площадки дальнего вида с помощью подобия. Так же в архитектуре применяется подобие, для измерения высоты зданий и сооружений. Я заинтересовалась, а как можно измерить высоту 10 этажного дома не поднимаясь на нее. Изучив литературу, я узнала о различных способов измерения высоты и выбрала из них шесть. Провела измерения следующих объектов: 10 этажного дома, дерева, частного дома, магазина и школы. Затем составила таблицы с измерениями и вычислила погрешность. Построила графики по данным результатам. В ходе исследования самым точным способом оказался способ с помощью зеркала.
Я так же измерила путь от дома до школы с помощью подобия. Точность этих измерений я не могу определить, так как не знаю реальное расстояние, но хоть мой результат и не точен, я узнала примерную длину моего пути.
В интернете я нашла интересную задачу с монетой. Решила ее и подумала, что я могу разработать свой способ измерения высоты при помощи монеты. Спустя долгое время мне удалось это сделать. Измерив данным способом высоту десятиэтажного дома я выяснила, что результат приближен к реальной высоте дома, и решила, что мой способ вполне можно использовать при измерении высоты. Подобие применяется от школьной тетради вплоть до вселенной.
Я считаю свою работу перспективной, потому, что я могу попрактиковать другие способы измерения высоты, с которыми мне предстоит познакомиться.
Проектно-исследовательская работа Подобие треугольников в реальной жизни
Работа построениа на исследовании возможности применения подобия треугольников в реоальной жизни, выполнены эксперименты по измерению длины с помощью высотомера.
Просмотр содержимого документа
«11Сушко-t.doc»
ПОДОБИЕ ТРЕУГОЛЬНИКОВ В РЕАЛЬНОЙ ЖИЗНИ
Сушко Дарья Олеговна
Ученица 8 класса
Икаева Марина Александровна
Учитель математики, II категория
Геометрия зародилась в глубокой древности. Мир, в котором мы живем сегодня, также наполнен геометрией. Все предметы, окружающие нас, имеют геометрические формы. Это здания, улицы, растения, предметы обихода. В повседневной жизни часто встречаются фигуры одинаковой формы, но разного размера. Такие фигуры в геометрии называют подобными. Моя работа посвящена подобию треугольников, так как, изучая эту тему на уроках математики, меня заинтересовало, как на практике применяются понятие подобия треугольников и признаки подобия. Актуальность моей темы заключается в том, что без каких — либо инструментов, только опираясь на подобие треугольников, можно измерить высоту столба, колокольни, дерева, ширину реки, озера, оврага, длину острова, глубину пруда и т.д.
Целью работы было найти области применения подобия треугольников в реальной жизни.
Задачами работы были
изучить литературу по данной теме;
изучить историю возникновения понятия подобия;
узнать, где применяется подобие треугольников;
измерить высоту столба при помощи подобия треугольников различными способами;
Объекты и предметы исследования: высота: столб; дерево, модель пирамиды.
В ходе работы были применены следующие методы: обзор литературы, практическая работа, сравнение.
Работа носит практико-ориентированный характер, так как практическая значимость работы заключается в возможности использования результатов исследования на уроках геометрии, в повседневной жизни.
В результате выполнения работы были проведены измерения высоты столба, дерева, моделей, изготовленных автором.
Просмотр содержимого документа
«Подобие треугольников в реальной жизни»
Легенда об измерении Фалесом высоты пирамиды
Понятие подобия фигур. Признаки подобия.
4.1 Определение высоты по тени
4.2. Измерение высоты методом Жюля Верна
4.3. Измерение высоты с помощью высотомера
Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои знания о форме, размерах и взаимном расположении предметов, полученные из наблюдений и опытов. Мир, в котором мы живем сегодня, также наполнен геометрией. Все предметы, окружающие нас, имеют геометрические формы. Это здания, улицы, растения, предметы обихода. В повседневной жизни часто встречаются фигуры одинаковой формы, но разного размера. Такие фигуры в геометрии называют подобными. Моя работа посвящена подобию треугольников, так как, изучая эту тему на уроках математики, меня заинтересовало, как на практике применяются понятие подобия треугольников и признаки подобия. Актуальность моей темы заключается в том, что без каких — либо инструментов, можно измерить высоту столба, колокольни, дерева, ширину реки, озера, оврага, длину острова, глубину пруда и т.д.
Целью моей работы было найти области применения подобия треугольников в реальной жизни.
Задачами моей работы были
изучить литературу по данной теме;
изучить историю возникновения понятия подобия;
узнать, где применяется подобие треугольников;
измерить высоту столба при помощи подобия треугольников различными способами;
2. Легенда об измерении Фалесом высоты пирамиды.
С пирамидой связано много таинственных историй и легенд. В один из жарких дней Фалес вместе с главным жрецом храма Изиды прогуливался мимо пирамиды Хеопса.
— Знает ли кто – либо, какова её высота?- спросил он.
— Нет, сын мой, — ответил ему жрец,- древние папирусы не сохранили нам этого. — Но ведь определить высоту пирамиды можно совсем точно и прямо сейчас!- воскликнул Фалес.
— Вот смотрите,- продолжал Фалес,- именно в это время, какой бы мы предмет не взяли, тень от него, если поставить его вертикально, точно высоте предмета! Чтобы воспользоваться тенью для решения задачи о высоте пирамиды, надо было знать уже некоторые геометрические свойства треугольника, — именно следующие два (из которых первое Фалес открыл сам):
1. Что углы при основании равнобедренного треугольника равны, и обратно – что стороны, лежащие против равных углов треугольника, равны между собою; 2. Что сумма углов всякого треугольника равна двум прямым углам.
Только вооружённый этим знанием Фалес вправе был заключить, что, когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и следовательно, вершина пирамиды, середина её основания и конец её тени должны обозначить равнобедренный треугольник . Этим простым способом очень удобно, казалось бы, пользоваться в ясный солнечный день для измерения одиноко стоящих деревьев, тень которых не сливается с тенью соседних. Но в наших широтах не так легко, как в Египте, подстеречь нужный для этого момент: Солнце у нас низко стоит над горизонтом, и тени бывают равны высоте отбрасывающих их предметов лишь в околополуденные часы летних месяцев. Поэтому способ Фалеса в указанном виде применим не всегда.
Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V— IV вв. до н. э. Оно изложено в VI книге «Начал» Евклида(III век до нашей эры), начинающиеся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны»
3. Понятие подобных фигур.
В жизни мы встречаемся не только с равными фигурами, но и с такими, которые имеют одинаковую форму, но разные размеры. Геометрия называет такие фигуры подобными. Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника. Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.
Признаки подобия треугольников.
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
4. Измерительные работы с помощью подобия.
4.1. Определение высоты по тени.
Я решила провести эксперимент по определению высоты по тени.
Для этого мне понадобились: фонарик, макет пирамиды, фигурка. Сделать миниатюрную пирамиду для проведения экспериментов несложно. Мне понадобились: лист бумаги; карандаш; линейка; ножницы; клей для бумаги. На листе бумаги я построила развертку пирамиды, в основании которой квадрат со стороной 7,6 см, а баковые грани – равные равнобедренные треугольники с боковой стороной 9,6 см. Высота получившейся пирамиды – 7,9 см. Высота фигурки 8,1 см. Попробуем измерить высоту данной пирамиды по её тени, используя также тень фигурки. В солнечный день я измерила тень пирамиды и фигурки. У меня получилось: 15см — тень фигурки, 13 см — тень пирамиды.
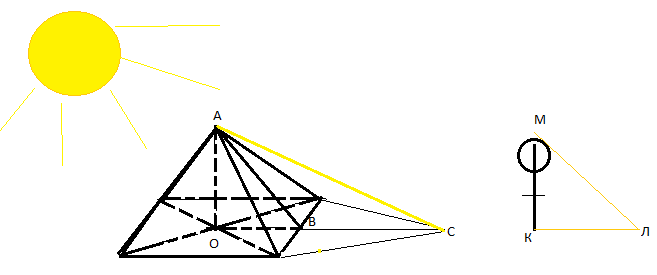
Построим геометрическую модель данной задачи:
Исходные данные задачи: Длина тени пирамиды ВС = 11 см, длина тени фигурки КЛ =15 см, высота фигурки КМ=8 см, основание пирамиды – квадрат со стороной 7,6 см. Высота пирамиды АО – искомое.
Рассмотрим прямоугольные треугольники АОС и МКЛ:
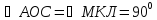
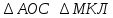
Найдем теперь высоту пирамиды другим способом для сравнения результатов. Найдем высоту боковой грани: АВ=
Из 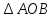
Мы получили практически одинаковые результаты. Получив такие результаты, я решила измерить высоту столба, выйдя на улицу.
Я выбрала столб, от которого падала четкая тень и измерила её. Она равнялась 21 м. Затем я стала рядом со столбом и мой помошник измерил мою тень, она равнялась 4,5 метра. Мой рост, учитывая, что я была в обуви и головном уборе, составил 1,6 .
Найдем высоту столба, составив геометрическую модель задачи.
Рассмотрим 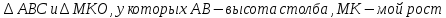
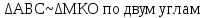
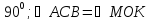
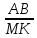
Таким образом, я получила приблизительное значение высоты столба 7,46 м.
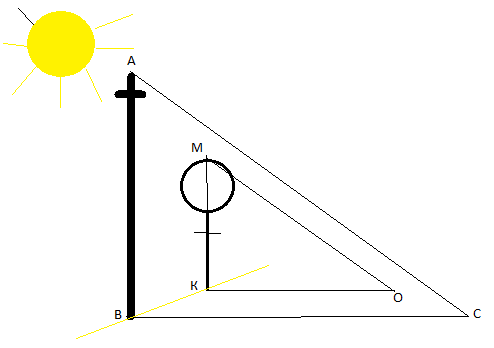
4.2. Измерение высоты пирамиды методом Жюля Верна.
«Таинственный остров» описывает интересный способ определения высоты: «Юноша, стараясь научиться возможно большему, последовал за инженером, который спустился с гранитной стены до окраины берега. Взяв прямой шест, футов 12 длиною, инженер измерил его возможно точнее, сравнивая со своим ростом, который был ему хорошо известен. Герберт же нес за ним отвес, врученный ему инженером: просто камень, привязанный к концу веревки. Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса Затем он отошел от шеста на такое расстояние, чтобы, лежа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. эту точку он тщательно пометил колышком.
— Тебе знакомы начатки геометрии? — спросил он Герберта, поднимаясь с земли.
— Помнишь свойства подобных треугольников?
— Их сходственные стороны пропорциональны. — Правильно. Так вот: сейчас я построю два подобных прямоугольных треугольника. У меньшего одним катетом будет отвесный шест, другим — расстояние от колышка до основания шеста; гипотенуза же — мой луч зрения. У другого треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же — мол луч зрения, совпадающий с направлением гипотенузы первого треугольника.
— Понял!—воскликнул юноша.—Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены. — Да. И следовательно, если мы измерим два первых расстояния, то, зная высоту шеста, сможем вычислить четвертый, неизвестный член пропорции, т. е. высоту стены. Mы обойдемся, таким образом, без непосредственного измерении этой высоты. Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее — 500 футам. По окончании измерений инженер составил следующую запись:
15 : 500 = 10:х, 500 X 10 = 5000, 5000 : 15 = 333,3.
4.3 Определение высоты с помощью высотомера
Высоту можно измерить специальным прибором — высотомером. Для изготовления данного прибора потребуется: Плотный белый картон, линейка, ручка, карандаш, ножницы, нитка, грузик, игла.
1. Из картона чертим и вырезаем квадрат размером 15х15см.
2. Делим квадрат на два прямоугольника: 5х15 см, 10х15 см.
3. Прямоугольник 10х15 см делим на две части: 5 см и 10 см.
4. На большей части с длиной 10 см, наносим сантиметровые деления и обозначаем их десятичной дробью, то есть 0,1;0,2 и т.д.
5. В точке Е иглой делаем отверстие и протаскиваем нитку с грузиком, а затем закрепляем нитку сзади.
6. Для того, чтобы было удобнее смотреть, отгибаем верхний прямоугольник от основания.
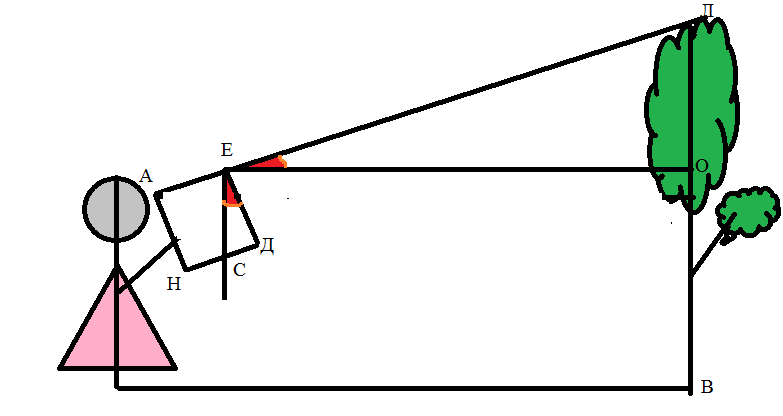
7. На нём с боков отгибаем два прямоугольника размером 3х5 см и прорезаем два отверстия с разным диаметром: одной поменьше — у глаза, другой побольше – для того, чтобы навести на вершину дерева. Итак, я решила провести эксперимент и проверить данный способ измерения высоты предмета. В качестве измеряемого объекта я выбрала дерево, растущее возле школы.
Я отошла от измеряемого предмета на 21 шаг, то есть EO =6,3 м. Я измерила показания прибора, он показывал 0,7. Мой рост 1,6 м. Требуется найти высоту дерева.
Для этого построим геометрическую модель данной задачи:
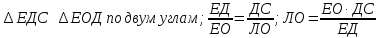
Прибавим к полученной величине мой рост и получим: ЛВ=ЛО+ОВ=3,71
1,6=5,31 – высота дерева.
Также, я могла допустить ошибки в использовании прибора Ошибки в использовании и изготовлении прибора:
1.Если не отгибать верхний прямоугольник от основания, то вы неправильно определите высоту.
2.При измерении высоты предмета, грузик должен быть направлен на конкретную величину разметки.
3.Расстояние от измеряемого объекта должно быть точным.
4.Точно наносить разметку в 1 см.
Эксперимент показал, что метод определения высоты предмета с помощью прибора «высомера» является более точным и удобным.
Выполнив свою работу я узнала о том, что существуют много различных способов определения высоты предмета. Я провела эксперимент по определению высоты предмета по его тени. Испытание я проделала в домашних условиях на модели пирамиды и фигурки, а также на улице при измерении высоты столба. Также, я рассмотрела способ Жюля Верна для определения высоты. Я изучила понятие высотометра и изготовила прибор высотометр, который применила на практике для измерения высоты выбранного объекта. Самым удобным способом измерения высоты для меня пришлось использование высотометра. Таким образом, цели моей работы достигнуты. Можно смело утверждать, что подобие треугольников применяется в реальной жизни при измерительных работах на местности.
1. Глейзер Г.И. История математики в школе. – М.:Издательство «Просвещение», 1964.
2.Перельман Я. И. Занимательная геометрия.– М.:Государственное издательство технико-теоретической литературы, 1950.
3.Ж.Верн. Таинственный остров.- М: Издательство « Детская литература», 1980.
4. Геометрия, 7 – 9: учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 18-е изд. – М.: Просвещение, 2010 Использованные материалы и интернет-ресурсы .
5. Перельман Я. И. Занимательная геометрия.– М.:Государственное издательство технико-теоретической литературы, 1950
Измерять высоту дерева можно 3-мя способами.