Подобные треугольники в природе

Класс: 8

Презентации к уроку

Природа говорит языком математики:
буквы этого языка — круги, треугольники
и иные математические фигуры.
Галилей

Цели и задачи урока:

Образовательные

• показать применение подобия треугольников при проведении измерительных работ на местности;
• показать взаимосвязь теории с практикой;
• познакомить учащихся с различными способами определения высоты предмета и расстояния до недоступного объекта;
• формировать умения применять полученные знания при решении разнообразных задач данного вида.

Развивающие

• повышать интерес учащихся к изучению геометрии;
• активизировать познавательную деятельность учащихся;
• формировать качества мышления, характерные для математической деятельности и необходимые для продуктивной жизни в обществе.

Воспитательные

• мотивироватьинтерес учащихся к предмету посредством включения их в решение практических задач.

Используемые ТСО:

• проектор, ноутбук, интерактивная доска.

Ход урока

Слайды 1-2 (Презентация 1)

Геометрия — одна из самых древних наук. Она возникла на основе практической деятельности людей и в начале своего развития служила преимущественно практическим целям. В дальнейшем геометрия сформировалась как самостоятельная наука, занимающаяся изучением геометрических фигур.

Геометрические знания широко применяются в жизни — в быту, на производстве, в науке. При покупке обоев надо знать площадь стен комнаты; при изготовлении технических чертежей — выполнять геометрические построения; при определении расстояния до предмета, наблюдаемого с двух точек зрения, нужно пользоваться известными вам теоремами.

Геометрия всегда решала те задачи, которые перед ней ставила жизнь. Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, многие детские игрушки подобны предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию. В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например футбольный и теннисный мячи, две фотографии разного формата.

Мы уже знаем, что в геометрии фигуры одинаковой формы принято называть подобными. Сегодня мы обсудим, как свойства подобных треугольников могут быть использованы для проведения различных измерительных работ на местности.

При помощи подобных треугольников можно измерить огромные расстояния и высоты используя подручные средства, т.е. мы будем решать две задачи:

• определение высоты предмета;
• определение расстояния до недоступного объекта.

Для начала в этом нам помогут герои известного мультфильма «Шрек».

Начнем мы со сказки День Рождения Шрека или Практическое применение подобия треугольников. (Презентация 2)

Слайд 3 (Презентация 1)

Уже в XVI в. В России нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как землю верстать». Оно является частью «Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сводятся к определенным приемам решения задач на нахождение расстояний.

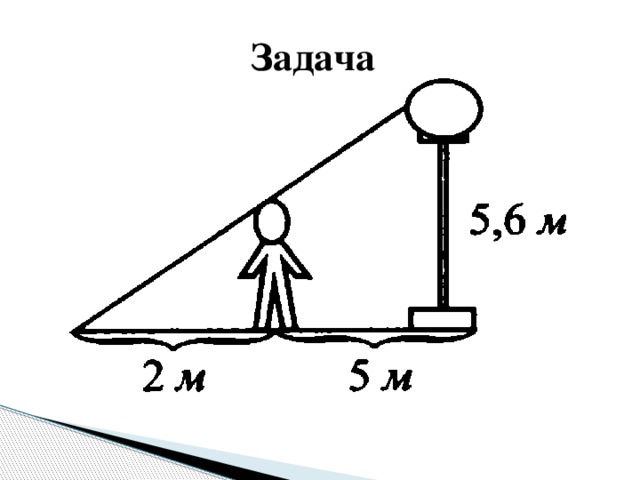
Слайд 4 (Презентация 1) Вот один пример.Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнемуконцужезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка З пересечения другого катета (или его продолжения) с землей. Тогда расстояние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Дляудобства расчетов и измерений жезл был разделен на 1000 равных частей.

Рассмотрим несколько случаев из истории и литературы.

1. Определение высоты предмета по длине его тени.

Слайд 5-7 (Презентация 1)

Греческие ученые решили множество практических задач, которые до них люди не умели решать. Например, за шесть веков до нашей эры греческий мудрец Фалес Милетский научил египтян определять высоту пирамиды по длине ее тени.

Как это было, рассказывается в книге Я.И. Перельмана «Занимательная геометрия».Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени.

Слайд 8 (Презентация 1)

Я хочу прочитать вам эту маленькую притчу.

«Усталый северный чужеземец пришел в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона и что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы.

— Кто ты? — спросил верховный жрец.

— Зовут меня Фалес. Родом я из Милета.

Жрец надменно продолжал:

— Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на нее? — жрецы согнулись от хохота.

— Будет хорошо, — насмешливо продолжал жрец, — если ты ошибешься не более, чем на сто локтей.

— Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.

Лица жрецов потемнели. Какая наглость! Этот чужестранец утверждает, что может вычислить то, чего не могут они — жрецы Великого Египта.

— Хорошо, сказал фараон. — Около дворца стоит пирамида, мы знаем ее высоту. Завтра проверим твое искусство».

Слайд 9-11 (Презентация 1)

На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Он измерил тень от палки и тень от пирамиды. Сравнивая соотношения высот реальных предметов с длинами их теней, Фалес нашел высоту пирамиды.

Определение высоты пирамиды по длине ее тени.

ВС — длина палки, DE — высота пирамиды.

АВС подобен D СDE (по двум углам):

ВСА= СED=90°;

АВС= СDЕ, т. к. соответственные при АВ || DС и секущей АС (солнечные лучи падают параллельно)

В подобных треугольниках сходственные стороны пропорциональны:

.

Таким образом, Фалес нашел высоту пирамиды.

Вопрос классу: Однако, способ предложенный Фалесом, применим не всегда. Почему?

Преимущества способа Фалеса:

• не требуются вычисления.

Недостатки:

• нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени.

2. Определение высоты предмета по шесту.

Слайд 12-15 (Презентация 1)

При отсутствии тени в пасмурную погоду можно воспользоваться способом измерения, которыйживописнопредставлен у Жюль Верна в известном романе «Таинственный остров».

Читаем отрывок из романа.

«:- Сегодня нам надо измерить высоту площадки скалы Дальнего вида, — сказал инженер.

— Вам понадобится для этого инструмент? — спросил Герберт.

— Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу.

Юноша, стараясь научиться, возможно, большему, последовал за инженером, который спустился с гранитной стены до окраины берега.

Взяв прямой шест, длиной 10 футов, инженер измерил его возможно точнее, сравнивая со своим ростом, который был хорошо ему известен. Герберт нёс за ним отвес, вручённый ему инженером: просто камень, привязанный к концу верёвки.

Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно отметил колышком.

— Тебе знакомы зачатки геометрии? — спросил он Герберта, поднимаясь с земли.

— Помнишь свойства подобных треугольников?

— Их сходственные стороны пропорциональны.

— Правильно. Так вот: сейчас я построю 2 подобных прямоугольных треугольника. У меньшего одним катетом, будет отвесный шест, другим — расстояние от колышка до основания шеста; гипотенуза же — мой луч зрения. У другого треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же — мой луч зрения, совпадающий с направлением гипотенузы первого треугольника.

— Понял! — воскликнул юноша. — Расстояние от колышка до шеста так относится к расстоянию к расстоянию от колышка до основания стены, как высота шеста к высоте стены.

— Да, и, следовательно, если мы измерим два расстояния, то зная высоту шеста, сможем вычислить четвёртый неизвестный член пропорции, т.е. высоту стены. Мы обойдёмся, таким образом, без непосредственного измерения этой высоты.

Оба расстояния были измерены. Расстояние от колышка до палки равнялось 15 футам, а от палки до скалы 485 футам.

По окончании измерений инженер составил следующую запись:

Н 333,33

Значит, высота гранитной стены равнялась приблизительно 333 футам».

Преимущества способа Жюль Верна:

— можно производить измерения в любую погоду;

Недостатки:

• нельзя измерить, высоту предмета не испачкавшись, так как приходится ложиться на землю.

3. Определение высоты предмета.

Есть несколько простых способов определения высоты предметов. Например, такие способы приведены в настольной книге охотника-спортсмена.

Слайд 16 (Презентация 1)

По луже. Этот способ можно удачно применять после дождя, когда на земле появляется много лужиц. Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершина предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас.

Слайд 17-18 (Презентация 1)

Вместо лужицы можно пользоваться положенным горизонтально зеркальцем. Зеркало кладут горизонтально и отходят от него назад в такую точку, стоя в которой, наблюдатель видит в зеркале верхушку дерева. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека.

АВD подобен D EFD (по двум углам):

ВАD = FED=90°;

АDВ = EDF, т.к. угол падения равен углу отражения.

В подобных треугольниках сходственные стороны пропорциональны:

; .

Таким образом, найдена высота объекта.

4. Определение расстояния до недоступного объекта.

Рассмотрим применение подобия треугольников к определению расстояния до недоступного объекта. Слайд 19-25 (Презентация 1, с использованием Приложения 1).

5. Практическое задание. Слайд 26 (Презентация 1)

Предлагается решить задачу № 583.В ней предлагается, применив подобие треугольников, измерить ширину реки.Чертеж к задаче имеется в учебнике. Ученикам необходимо объяснить, как получен такой чертеж, доказать подобие треугольников и провести вычисления.

По построению АВС подобен АВ₁С₁ (по двум углам).

В подобных треугольниках сходственные стороны пропорциональны:

;;;

6. Рассмотрение и обсуждение примеров. Слайды 27-28 (Презентация 1).

7. Дополнительный материал. Слайд 29-30 (Презентация 1 с использованием Приложения 1)

Для «проведения» длинных отрезков на местности используют прием, называемый провешиванием прямой. Этот прием заключается в следующем: сначала отмечают какие-нибудь точки А и В. Для этой цели используют две вехи — шесты длиной около 2 м, заостренные на одном конце для того, чтобы их можно было воткнуть в землю. Третью веху (точка С) ставят так, чтобы вехи, стоящие в точках А и В, закрывали ее от наблюдателя находящегося в точке А. Следующую веху ставят так, чтобы ее закрывали вехи, стоящие в точках В и С, и т.д.

Измерение углов на местности можно провести с помощью специального прибора — астролябия. Астролябия состоит из двух частей: диска, разделенного на градусы, и вращающегося вокруг центра диска линейки (алидады). На концах алидады находятся два узких окошечка, которые используются для установки ее в определенном направлении. Для того чтобы измерить АОВ на местности, треножник с астролябией ставят так, чтобы отвес, подвешенный к центру диска, находился точно над точкой О. Затем устанавливают алидаду вдоль одной из сторон ОА или ОВ, и отмечают деление, против которого находится указатель алидады. Далее поворачивают алидаду, направляя ее вдоль другой стороны измеряемого угла, и отмечают деление, против которого окажется указатель алидады. Разность отсчета и дает градусную меру АОВ.

8. Подведение итогов.

Домашнее задание: пункт 64 параграфа 3, стр. 150-151, № 581, 582, придумать свои задачи на определение высоты предмета и определение расстояния до недоступной точки (оформить либо в виде презентации, либо в виде практической работы в формате А4).

9. Выступления учащихся на следующем уроке с домашним заданием по теме. Выбраны, как примеры, некоторые презентации учеников разных классов — 8 «А» историко-филологического и 8 «Г» физико-математического — в этих классах я работала в том учебном году, когда проходили данную тему. Сейчас эти ребята учатся в десятом классе. (Презентации 3-9).

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Применение подобия в реальной жизни (презентация)

Скажи мне и я забуду,

Покажи, и я запомню.

Дай мне действовать самому

Китайская мудрость

Урок, обучающий учащихся применять на практике подобия треугольников

Просмотр содержимого документа
«Применение подобия в реальной жизни (презентация)»

Скажи мне и я забуду,

Покажи, и я запомню.

Дай мне действовать самому

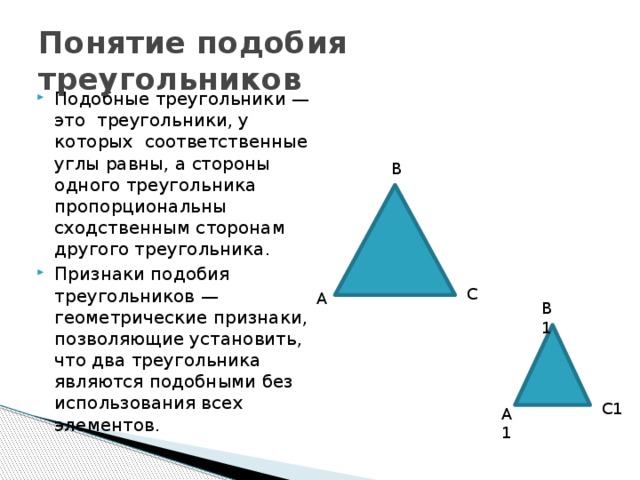
Понятие подобия треугольников

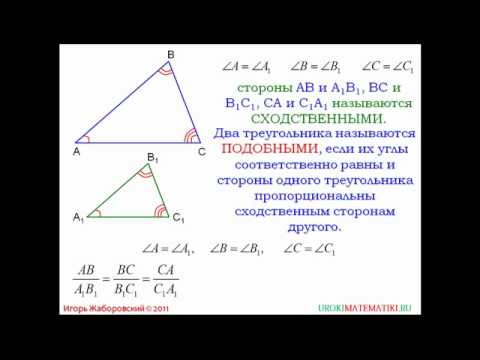
• Подобные треугольники —это треугольники, у которых соответственные углы равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
• Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов.

Применение в жизни

• В технике

В судоходном деле

Подобие в природе

Применение подобия треугольников в жизни

• Закрепить понятие подобия треугольников
• Узнать где применяется подобие в жизни

(ок. 624 — ок. 546 до н.э.)

Определение высоты пирамиды

по длине ее тени

Способ Жуль Верна

Нахождения четвертого неизвес неизвестного члена

Определение высоты предмета

Определение высоты предмета

 АВ D подобен  EFD (по двум углам) :

• А DВ =  EDF, т.к. угол падения равен углу отражения.

В подобных треугольниках сходственные стороны пропорциональны :

• Подобие треугольников применяется в повседневной жизни довольно часто. Мы выяснили на конкретных примерах, что с помощью подобия можно найти высоту до неизвестной нам точки.

1. Шла баба в Москву и повстречала трёх мужиков. Каждый из них нёс по мешку, в каждом мешке по кошке. Сколько существ направлялось в Москву?

• Летела стая гусей: один гусь впереди, а два позади, один позади, и два впереди; один между двумя и три в ряд. Сколько было гусей?

3. Две женщины отправились в Троице-Сергиеву Лавру. Обе они прошли 60 вёрст. Сколько вёрст прошла каждая, если шли они с одинаковой скоростью?

4. Какое число делится на все числа без остатка?

5.Электропоезд идёт с востока на запад, ветер дует с севера на юг. В какую сторону отклоняется дым?

6. На дереве сидело 10 птиц. Охотник выстрелил и подстрелил одну птицу. Сколько птиц осталось на дереве? *

• Используя признаки подобия, вычислите высоту здания своей школы и высоту потолка в своей комнате.

• По желанию

Используя карточку определите ширину реки с помощью травинки.

• Я узнал…
• Я научился…
• Мне понравилось…
• Я затруднялся…
• Моё настроение…

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

«Подобие фигур в жизни»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ pril1.ppt

Описание презентации по отдельным слайдам:

Уже в XVI в. нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как землю верстать». Оно является частью «Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сводятся к определенным приемам решения задач на нахождение расстояний.

Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнему концу жезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка З пересечения другого катета (или его продолжения) с землей. Тогда расстояние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Для удобства расчетов и измерений жезл был разделен на 1000 равных частей. Вот один пример из «Устава ратных, пушечных и других дел, касающихся до военной науки»:

За шесть веков до нашей эры греческий мудрец Фалес Милетский вычислил высоту египетской пирамиды, измерив длину её тени. Как это было, рассказывается в книге Я.И.Перельмана «Занимательная геометрия». Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени. ПРИТЧА:

« Усталый чужеземец пришёл в страну Великого Хапи. Солнце уже садилось, когда он подошёл к великолепному дворцу фараона. Он что-то сказал слугам. По мановению руки распахнулись перед ним двери и провели его в приёмную залу. И вот он стоит в запылённом походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители великих тайн природы. — Кто ты? – спросил верховный жрец. — Зовут меня Фалес. Родом я из Милета. Жрец надменно продолжал: — Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на неё? – Жрецы согнулись от хохота. — Будет хорошо, — насмешливо продолжал жрец, — если ты ошибёшься не более чем на 100 локтей. — Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра. Лица жрецов потемнели. Какая наглость! Этот чужеземец утверждает, что может вычислить то, чего не могут они – жрецы великого Египта. — Хорошо, — сказал фараон. – Около дворца стоит пирамида, мы знаем её высоту. Завтра проверим твоё искусство».

На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту.

Когда тень от палки будет той же длины, что и сама палка, то длина тени от центра основания пирамиды до её вершины будет иметь ту же длину, что и сама пирамида. СЕ=ED, т.е. H=b Преимущества: не требуются вычисления. Недостатки: нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени.

«Таинственный остров» (фр. L’Île mystérieuse) — роман-робинзонада французского писателя впервые опубликованный в 1874 году. Является продолжением известных произведений Верна «20000 лье под водой» и «Дети капитана Гранта». В книге повествуется о событиях, происходящих на вымышленном острове, где остановился капитан Немо на своей подводной лодке «Наутилус». Основными персонажами являются пятеро американцев, которые оказываются на необитаемом острове в Южном полушарии.

Нахождения четвертого неизвестного члена пропорции. Преимущества: можно производить измерения в любую погоду; простота формулы. Недостатки: нельзя измерить высоту предмета не испачкавшись, так как приходится ложиться на землю.

 АВD подобен EFD (по двум углам):  ВАD= FED=90°; АDВ = EDF, т.к. угол падения равен углу отражения. В подобных треугольниках сходственные стороны пропорциональны: ; . ; . ; .

Преимущества: можно производить измерения в любую погоду; одежда будет чистой; простота формулы; Недостатки: нужно специальное приспособление: зеркало.

По построению  АВС подобен  А1В1С1 (по двум углам). В подобных треугольниках сходственные стороны пропорциональны: А В С А1 В1 С1

Нахождение ширины озера Длина тени земного шара

Выбранный для просмотра документ Природа говорит языком математики.doc

Природа говорит языком математики.

Природа говорит языком математики:
буквы этого языка — круги, треугольники
и иные математические фигуры.
Галилей

Геометрия — одна из самых древних наук. Она возникла на основе практической деятельности людей и в начале своего развития служила преимущественно практическим целям. В дальнейшем геометрия сформировалась как самостоятельная наука, занимающаяся изучением геометрических фигур.

Геометрические знания широко применяются в жизни — в быту, на производстве, в науке. При покупке обоев надо знать площадь стен комнаты; при изготовлении технических чертежей — выполнять геометрические построения; при определении расстояния до предмета, наблюдаемого с двух точек зрения, нужно пользоваться известными вам теоремами.

Геометрия всегда решала те задачи, которые перед ней ставила жизнь. Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, многие детские игрушки подобны предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию. В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например футбольный и теннисный мячи, две фотографии разного формата.

Мы уже знаем, что в геометрии фигуры одинаковой формы принято называть подобными. Сегодня мы обсудим, как свойства подобных треугольников могут быть использованы для проведения различных измерительных работ на местности.

При помощи подобных треугольников можно измерить огромные расстояния и высоты используя подручные средства, т.е. мы будем решать две задачи:

определение высоты предмета;

определение расстояния до недоступного объекта.

Уже в XVI в. В России нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как землю верстать». Оно является частью «Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сводятся к определенным приемам решения задач на нахождение расстояний.

Вот один пример. Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнему концу жезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка З пересечения другого катета (или его продолжения) с землей. Тогда расстояние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Для удобства расчетов и измерений жезл был разделен на 1000 равных частей.

Рассмотрим несколько случаев из истории и литературы.

1. Определение высоты предмета по длине его тени.

Греческие ученые решили множество практических задач, которые до них люди не умели решать. Например, за шесть веков до нашей эры греческий мудрец Фалес Милетский научил египтян определять высоту пирамиды по длине ее тени.

Как это было, рассказывается в книге Я.И. Перельмана «Занимательная геометрия».Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени.

Я хочу прочитать вам эту маленькую притчу.

«Усталый северный чужеземец пришел в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона и что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы.

— Кто ты? — спросил верховный жрец.

— Зовут меня Фалес. Родом я из Милета.

Жрец надменно продолжал:

— Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на нее? — жрецы согнулись от хохота.

— Будет хорошо, — насмешливо продолжал жрец, — если ты ошибешься не более, чем на сто локтей.

— Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.

Лица жрецов потемнели. Какая наглость! Этот чужестранец утверждает, что может вычислить то, чего не могут они — жрецы Великого Египта.

— Хорошо, сказал фараон. — Около дворца стоит пирамида, мы знаем ее высоту. Завтра проверим твое искусство».

На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Он измерил тень от палки и тень от пирамиды. Сравнивая соотношения высот реальных предметов с длинами их теней, Фалес нашел высоту пирамиды.

Определение высоты пирамиды по длине ее тени.

ВС — длина палки, DE — высота пирамиды.

АВС подобен D СDE (по двум углам):

ВСА= СED=90°;

АВС= СDЕ, т. к. соответственные при АВ || DС и секущей АС (солнечные лучи падают параллельно)

В подобных треугольниках сходственные стороны пропорциональны:

.

Таким образом, Фалес нашел высоту пирамиды.

Преимущества способа Фалеса:

не требуются вычисления.

нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени.

2. Определение высоты предмета по шесту.

При отсутствии тени в пасмурную погоду можно воспользоваться способом измерения, которыйживописнопредставлен у Жюль Верна в известном романе «Таинственный остров».

Читаем отрывок из романа.

«:- Сегодня нам надо измерить высоту площадки скалы Дальнего вида, — сказал инженер.

— Вам понадобится для этого инструмент? — спросил Герберт.

— Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу.

Юноша, стараясь научиться, возможно, большему, последовал за инженером, который спустился с гранитной стены до окраины берега.

Взяв прямой шест, длиной 10 футов, инженер измерил его возможно точнее, сравнивая со своим ростом, который был хорошо ему известен. Герберт нёс за ним отвес, вручённый ему инженером: просто камень, привязанный к концу верёвки.

Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно отметил колышком.

— Тебе знакомы зачатки геометрии? — спросил он Герберта, поднимаясь с земли.

— Помнишь свойства подобных треугольников?

— Их сходственные стороны пропорциональны.

— Правильно. Так вот: сейчас я построю 2 подобных прямоугольных треугольника. У меньшего одним катетом, будет отвесный шест, другим — расстояние от колышка до основания шеста; гипотенуза же — мой луч зрения. У другого треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же — мой луч зрения, совпадающий с направлением гипотенузы первого треугольника.

— Понял! — воскликнул юноша. — Расстояние от колышка до шеста так относится к расстоянию к расстоянию от колышка до основания стены, как высота шеста к высоте стены.

— Да, и, следовательно, если мы измерим два расстояния, то зная высоту шеста, сможем вычислить четвёртый неизвестный член пропорции, т.е. высоту стены. Мы обойдёмся, таким образом, без непосредственного измерения этой высоты.

Оба расстояния были измерены. Расстояние от колышка до палки равнялось 15 футам, а от палки до скалы 485 футам.

По окончании измерений инженер составил следующую запись:

Н 333,33

Значит, высота гранитной стены равнялась приблизительно 333 футам».

Преимущества способа Жюль Верна:

— можно производить измерения в любую погоду;

нельзя измерить, высоту предмета не испачкавшись, так как приходится ложиться на землю.

3. Определение высоты предмета.

Есть несколько простых способов определения высоты предметов. Например, такие способы приведены в настольной книге охотника-спортсмена.

По луже. Этот способ можно удачно применять после дождя, когда на земле появляется много лужиц. Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершина предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас.

Вместо лужицы можно пользоваться положенным горизонтально зеркальцем. Зеркало кладут горизонтально и отходят от него назад в такую точку, стоя в которой, наблюдатель видит в зеркале верхушку дерева. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека.

АВD подобен D EFD (по двум углам):

ВАD = FED=90°;

АDВ = EDF, т.к. угол падения равен углу отражения.

В подобных треугольниках сходственные стороны пропорциональны:

; .

Таким образом, найдена высота объекта.

4. Определение расстояния до недоступного объекта.

Рассмотрим применение подобия треугольников к определению расстояния до недоступного объекта. Слайд 19-25 (Презентация 1, с использованием Приложения 1 ).

6. Рассмотрение и обсуждение примеров. Слайды 27-28 (Презентация 1).

7. Дополнительный материал. Слайд 29-30

Для «проведения» длинных отрезков на местности используют прием, называемый провешиванием прямой. Этот прием заключается в следующем: сначала отмечают какие-нибудь точки А и В. Для этой цели используют две вехи — шесты длиной около 2 м, заостренные на одном конце для того, чтобы их можно было воткнуть в землю. Третью веху (точка С) ставят так, чтобы вехи, стоящие в точках А и В, закрывали ее от наблюдателя находящегося в точке А. Следующую веху ставят так, чтобы ее закрывали вехи, стоящие в точках В и С, и т.д.

Измерение углов на местности можно провести с помощью специального прибора — астролябия. Астролябия состоит из двух частей: диска, разделенного на градусы, и вращающегося вокруг центра диска линейки (алидады). На концах алидады находятся два узких окошечка, которые используются для установки ее в определенном направлении. Для того чтобы измерить АОВ на местности, треножник с астролябией ставят так, чтобы отвес, подвешенный к центру диска, находился точно над точкой О. Затем устанавливают алидаду вдоль одной из сторон ОА или ОВ, и отмечают деление, против которого находится указатель алидады. Далее поворачивают алидаду, направляя ее вдоль другой стороны измеряемого угла, и отмечают деление, против которого окажется указатель алидады. Разность отсчета и дает градусную меру АОВ.

🔥 Видео

Подобные треугольники с нуля до ОГЭ | Математика ОГЭ 2023 | УмскулСкачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

8 класс, 20 урок, Определение подобных треугольниковСкачать

Подобные треугольникиСкачать

Решение задач на тему "Подобные треугольники". 8 классСкачать

8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Подобные треугольники - 8 класс геометрияСкачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Подобные треугольникиСкачать

Геометрия 8 класс (Урок№15 - Признаки подобия треугольников.)Скачать

ПОДОБНЫЕ ТРЕУГОЛЬНИКИ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Подобные треугольникиСкачать

Задача на подобие треугольников 1частьСкачать

видеоурок "Определение подобных треугольников"Скачать

ПОДОБНЫЕ ТРЕУГОЛЬНИКИ 8 класс ЗАДАЧИ коэффициент подобияСкачать