Задание 8. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на π.
Найдем сначала длину образующей конуса из прямоугольного треугольника, в котором известны два катета (высота и радиус основания конуса). По теореме Пифагора получаем:

Площадь полной поверхности исходного конуса, равна

где l – длина образующей конуса; r – радиус основания конуса. Подставляя числовые значения, получаем:

или в виде 
§ 14. Конус (прямой круговой).
1. (Устно.) Радиус основания конуса 3 м, высота 4 м. Найти образующую.
2. (Устно.) Образующая конуса L наклонена к плоскости основания под углом в 30°. Найти высоту.
3. (Устно.) Радиус основания конуса R. Осевым сечением служит прямоугольный треугольник. Найти его площадь.
4. Отношение площади основания конуса к площади осевого сечения равно π. Найти угол наклона образующей к основанию.
5. Высота конуса H. На каком расстоянии от вершины надо провести плоскость параллельно основанию, чтобы площадь сечения была равна половине площади основания?
6. 1) Радиус основания конуса R. Через середину высоты проведена плоскость параллельно основанию. Найти площадь сечения.
2) Радиус основания конуса R. Определить площадь параллельного сечения, делящего высоту конуса в отношении т : п (от вершины к основанию).
7. Высота конуса 20, радиус его основания 25. Найти площадь сечения, проведённого через вершину, если его расстояние от центра основания конуса равно 12.
8. В равностороннем конусе (в осевом сечении—правильный треугольник) радиус основания R. Найти площадь сечения, проведённого через две образующие, угол между которыми равен 30°.
9. Высота конуса Н. Угол между высотой и образующей равен 60°. Найти площадь сечения, проведённого через две взаимно перпендикулярные образующие.
10. 1) В конусе, у которого высота равна радиусу основания R, проведена через вершину плоскость, отсекающая от окружности основания дугу в 90°. Определить площадь полученного сечения.
2) Через вершину конуса под углом в 45° к основанию проведена плоскость, отсекающая четверть окружности основания. Высота конуса равна 10 см. Определить площадь сечения.
11. Через середину высоты конуса проведена прямая параллельно образующей l. Найти длину отрезка прямой, заключённого внутри конуса.
12. Образующая конуса 13 см, высота 12 см. Конус этот пересечён прямой ММ, параллельной основанию; расстояние её от основания равно 6 см, а от высоты 2 см. Найти отрезок этой прямой, заключённый внутри конуса (черт. 23).
13. В конусе даны радиус основания R и высота Н. Определить ребро вписанного в него куба.
14. В конусе даны радиус основания R и высота Н. В него вписана правильная треугольная призма, у которой боковые грани—квадраты. Определить ребро этой призмы.
15. (Устно.) Высота конуса h = 6, радиус основания r = 8. Найти боковую поверхность.
16. (Устно.) Высота конуса h = 4, образующая а = 5. Найти полную поверхность.
17. Конусообразная палатка высотой в 3,5 м с диаметром основания в 4 м покрыта парусиной. Сколько квадратных метров парусины пошло на палатку?
18. Крыша силосной башни имеет форму конуса. Высота крыши 2 м. Диаметр башни 6 м. Сколько листов кровельного железа потребовалось для покрытия крыши, если лист имеет размеры 0,7×1,4 (м 2 ) и на швы пошло 10% требующегося железа?
19. Поверхность конического шпиля башни равна 250 м 2 , диаметр основания 9 м. Найти высоту шпиля.
20. 1) Определить величину поверхности, полученной вращением хорды около диаметра, выходящего из её конца, если диаметр равен 25 см, а хорда равна 20 см.
2) Из точки А на окружности радиуса r = 7 м проведена касательная АB = l = 24 м, а из её конца В — секущая ВОС через центр. Определить величину поверхности, которую описывает отрезок ВС секущей, вращаясь вокруг касательной.
21. Равнобедренный треугольник вращается вокруг своей высоты. Определить стороны этого треугольника, если его периметр равен 30 см, а полная поверхность тела вращения равна 60π см 2 .
22. Наибольший угол между образующими конуса равен 60°. Найти отношение боковой поверхности к площади основания конуса.
23. 1) Как относятся между собой площадь основания, боковая поверхность и полная поверхность в равностороннем конусе?
2) По высоте H равностороннего конуса определить его полную поверхность.
24. Как относится боковая поверхность равностороннего конуса к боковой поверхности равностороннего цилиндра, имеющего такую же высоту?
25. Найти зависимость между образующей и радиусом основания конуса, у которого боковая поверхность есть средняя пропорциональная между площадью основания и полной поверхностью.
26. 1) Какая должна быть зависимость между образующей конуса и радиусом основания, чтобы его полная поверхность была равновелика кругу, за радиус которого принята высота конуса?
2) Какая должна быть зависимость между образующей конуса и радиусом основания, чтобы его полная поверхность была равновелика кругу, радиус которого равен образующей конуса?
27. 1) Высота конуса 4, радиус основания 3; боковая поверхность конуса развёрнута на плоскость. Найти угол полученного сектора.
2) По радиусу основания R и образующей L определить угол в развёртке боковой поверхности конуса. (Рассмотреть особо случай равностороннего конуса.)
3) Вычислить угол в развёртке боковой поверхности конуса: а) если наибольший угол между образующими— прямой; b) если образующая составляет с плоскостью основания угол в 30°.
28. 1) Полукруг свёрнут в коническую поверхность. Найти угол между образующей и высотой конуса.
2) Радиус сектора равен 3 м; его угол 120°. Сектор свёрнут в коническую поверхность. Найти радиус основания конуса.
29. 1) Боковая поверхность конуса содержит 80 см 2 ; угол в её развёртке равен 112° 30′. Определить площадь основания.
2) Боковая поверхность конуса равна 10 см 2 и развёртывается в сектор с углом в 36°. Определить полную поверхность.
3) Боковой поверхностью конуса служит свёрнутая четверть круга. Определить полную поверхность этого конуса, если площадь его осевого сечения равна М.
Вписанный и описанный конус.
30. Если наибольший угол между образующими конуса равен 120°, то его боковая поверхность равновелика боковой поверхности цилиндра, имеющего те же самые основания и высоту. Доказать.
31. В равносторонний конус вписана правильная четырёхугольная пирамида. Как относятся боковые поверхности конуса и пирамиды?
32. В данном конусе радиус основания r = 39 см, а высота h = 52 см. В него вписан цилиндр такой высоты, что его боковая поверхность равновелика боковой поверхности малого конуса, стоящего на его верхнем основании. Определить высоту цилиндра.
33. В конус с высотой Н и образующей L вписан цилиндр, у которого боковая поверхность в п раз менее боковой поверхности конуса. Определить высоту цилиндра (L= l,5H; n = 4).
34. В конус вписан цилиндр, у которого полная поверхность равновелика боковой поверхности конуса. Наибольший угол между образующими конуса равен прямому. Доказать, что расстояние от вершины конуса до верхнего основания цилиндра равно половине образующей конуса.
Радиус основания конуса 3 м, высота 4 м. Найдите образующую l.
Задача из пособия: Погорелов А.В. 11 класс
21. Тела вращения
Решение
Видео:№534. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 120Скачать

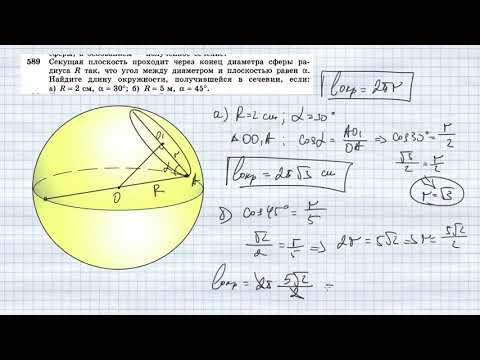
В конусе через его вершину под углом φ к плоскости основания проведена плоскость, отсекающая от окружности основания дугу а. Высота конуса равна
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Ваш ответ
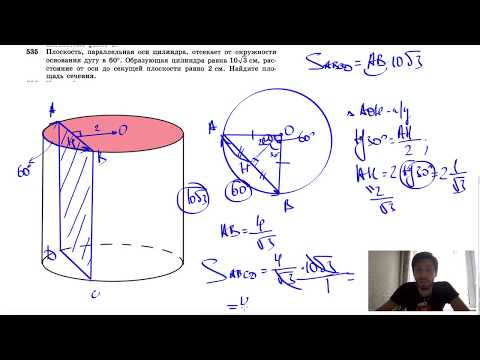
Видео:№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать
решение вопроса
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,857
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Плоскость отсекающая четверть окружности основания
рисунок 1 рисунок 2
Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга,— вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания (рис. 1) Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса. Поверхность конуса состоит из основания и боковой поверхности.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом. Наглядно прямой круговой конус можно представлять себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси (рис.2).
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту.
рисунок 3 рисунок 4
рисунок 5 рисунок 6
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 3). В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса (рис. 4).
Теорема. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность — по окружности с центром на оси конуса.
Доказательство. Пусть $$beta$$ — плоскость, параллельная плоскости основания конуса и пересекающая конус (рис.5). Преобразование гомотетии относительно вершины конуса, совмещающее плоскость $$beta$$ с плоскостью основания, совмещает сечение конуса плоскостью $$beta$$ с основанием конуса. Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности – окружность с центром на оси конуса. Теорема доказана.
Задача №1: Конус пересечен плоскостью, параллельной основанию, на расстоянии d от вершины. Найдите площадь сечения, если радиус основания конуса R, а высота H.
Решение. Сечение конуса получается из основания конуса преобразованием гомотетии $$k = frac$$ . Поэтому радиус круга в сечении $$r = R cdot frac$$ . Следовательно, площадь сечения $$S = pi r^ = R^cdot(frac)^$$.
Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом (рис. 6).
Пирамидой, вписанной в конус, называется такая пирамида, основание которой есть многоугольник, вписанный в окруж¬ность основания конуса, а вершиной является вершина конуса (рис. 7). Боковые ребра пирамиды, вписанной в конус, яв¬ляются образующими конуса.
 рисунок 7 рисунок 7 | Задача №2: У пирамиды все боковые ребра равны. Докажите, что она является вписанной в некоторый конус. Решение. Опустим перпендикуляр SO из вершины пирамиды на плоскость основания (рис. 7) и обозначим длину боковых ребер пирамиды через l. Вершины основания удалены от точки О на одно и то же расстояние. Отсюда следует, что наша пирамида вписана в конус, у которого вершиной является вершина пирамиды, а основанием — круг с центром О и радиусом R. |