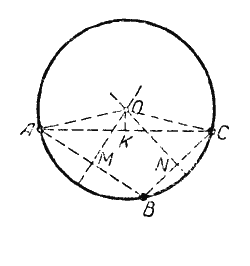
Пусть нам даны три точки А, В и С, не лежащие на одной прямой (см. рис.).
Соединим эти точки отрезками АВ и ВС. Чтобы найти точки равноудалённые от точек А и В разделим отрезок АВ пополам и через середину (точку М) проведём прямую перпендикулярную к АВ. Каждая точка этого перпендикуляра одинаково удалена от точек А и В.
Чтобы найти точки, равноудалённые от точек В и С, разделим отрезок ВС пополам и через его середину (точку N) проведемпрямую, перпендикулярную ВС. Каждая точка этого перпендикуляа одинаково удалена от точек В и С.
Точка О пересечения этих перпендикуляров будет находиться на одинаковом расстоянии от данных точек А, В и С (АО = ВО = СО). Если мы, приняв точку О за центр круга, радиусом, равным АО, проведём окружность, то она пройдёт через все данные точки А, В и С.
Точка О является единственной точкой, которая может служить центром окружности, проходящей через три точки А, В и С, не лежащие на одной прямой, так как два перпендикуляра к отрезкам АВ и ВС могут пересечься только в одной точке. Значит, задача имеет единственное решение.
Примечание. Если три точки А, В и С будут лежать на одной прямой, то задача не будет иметь решения, так как перпендикуляры к отрезкам АВ и ВС будут параллельны и не будет существовать точки, одинаково удаленной от точек А, В, С, т. е. точки, которая могла бы служить центром искомой окружности.
Если соединить отрезком точки А и С и середину этого отрезка (точку К) соединить с центром окружности О, то ОК будет перпендикулярна к АС (рис.), так как в равнобедренном треугольнике АОС ОК является медианой, поэтому ОК ⊥ АС.
Следствие. Три перпендикуляра к сторонам треугольника, проведённые через их середины пересекаются в одной точке.
Видео:Три точки, задающие окружностьСкачать
Please wait.
Видео:10 класс, 3 урок, Некоторые следствия из аксиомСкачать

We are checking your browser. mathvox.ru
Видео:Окружность. 7 класс.Скачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d8ec76e6c56169f • Your IP : 85.95.188.35 • Performance & security by Cloudflare
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Доказать что через три точки проходит только одна окружность
ОКРУЖНОСТЬ И КРУГ. ЦИЛИНДР.
§ 69. ПОСТРОЕНИЕ ОКРУЖНОСТИ ПО ТРЁМ ДАННЫМ ТОЧКАМ.
Задача. Через три точки, не лежащие на одной прямой, провести окружность.
Пусть нам даны три точки А, В и С, не лежащие на одной прямой (черт.311).
Соединим эти точки отрезками АВ и ВС. Чтобы найти точки равноудалённые от точек А и В разделим отрезок АВ пополам и через середину (точку М) проведём прямую перпендикулярную к АВ. Каждая точка этого перпендикуляра одинаково удалена от точек А и В (§ 27, п. 4).
Чтобы найти точки, равноудалённые от точек В и С, разделим отрезок ВС пополам и через его середину (точку N) проведем прямую, перпендикулярную ВС. Каждая точка этого перпендикуляа одинаково удалена от точек В и С.
Точка О пересечения этих перпендикуляров будет находиться на одинаковом расстоянии от данных точек А, В и С (АО = ВО = СО). Если мы, приняв точку О за центр круга, радиусом, равным АО, проведём окружность, то она пройдёт через все данные точки А, В и С.
Точка О является единственной точкой, которая может служить центром окружности, проходящей через три точки А, В и С, не лежащие на одной прямой, так как два перпендикуляра к отрезкам АВ и ВС могут пересечься только в одной точке. Значит, задача имеет единственное решение.
Примечание. Если три точки А, В и С будут лежать на одной прямой, то задача не будет иметь решения, так как перпендикуляры к отрезкам АВ и ВС будут параллельны и не будет существовать точки, одинаково удаленной от точек А, В, С, т. е. точки, которая могла бы служить центром искомой окружности.
Если соединить отрезком точки А и С и середину этого отрезка (точку К) соединить с центром окружности О, то ОК будет перпендикулярна к АС (черт. 311), так как в равнобедренном треугольнике АОС ОК является медианой, поэтому ОК _|_ АС.
Следствие. Три перпендикуляра к сторонам треугольника, проведённые через их середины пересекаются в одной точке.
📺 Видео
Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Как искать точки на тригонометрической окружности.Скачать

№5. Докажите, что через три данные точки, лежащие на прямой, проходит плоскость.Скачать

№3. Верно ли, что: а) любые три точки лежат в одной плоскости;Скачать

никакие три точки окружности не лежат на одной прямойСкачать
✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Стереометрия - это ПРОСТО! Урок 1. Аксиомы Теоремы Задачи. Геометрия 10 классСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

ЕГЭ Задание 16 Докажите, что три точки лежат на одной прямойСкачать