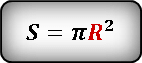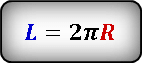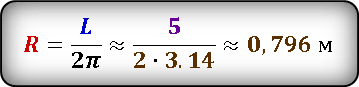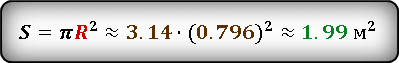Площадь окружности равна s найдите длину ограничивающей его окружности (6 видео)

Решение задач по материалу главы XII — ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА

Цели: закрепить знания и умения учащихся по изученному материалу главы; подготовить учащихся к контрольной работе.

I. Математический диктант (15 мин).

1. Площадь круга равна S. Найдите длину ограничивающей его окружности.

2. Найдите длину дуги окружности радиуса 9 м, если градусная мера дуги равна 120°.

3. Длина дуги окружности равна 3π, а ее радиус равен 8. Найдите градусную меру этой дуги.

4. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см.

5. Найдите площадь кругового сектора радиуса 4 см, если его центральный угол равен 45°.

6. Площадь кругового сектора равна 18π м2, а его центральный угол равен 40°. Найдите радиус сектора.

1. Длина окружности равна С. Найдите площадь ограниченного ею круга.

2. Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 25 и 24 см.

3. Найдите площадь кругового сектора радиуса 3 см, если его центральный угол равен 20°.

4. Площадь кругового сектора равна 10π м2, а его радиус равен 6 м. Найдите центральный угол сектора.

5. Найдите длину дуги окружности радиуса 6 дм, если ее градусная мера равна 120°.

6. Найдите радиус окружности, если длина дуги окружности равна 6π, а ее градусная мера равна 60°.

II. Решение задач.

1. Решить задачу 1. Докажите, что площадь S треугольника АВС вычисляется по формуле.

где Р – периметр треугольника, r – радиус вписанной окружности.

Пусть О – центр окружности, которая вписана в треугольник АВС и, следовательно, касается сторон треугольника в точках М, N и K.

Очевидно, что S = SАОС + SВОС + SАОВ. *

Так как ОМ, ОN и ОK – высоты треугольников АОС, ВОС и АОВ, то SАОС = АС · ОK, SВОС = ВС · ОМ и SАОВ = АВ · ОN.

Подставив эти значения в формулу *, получим: S = (AB + BC + CA) · r = P · r.

2. Решить задачу 2. даны стороны треугольника АВС – а, b, с и площадь S. Выразить радиусы окружностей, описанной около треугольника и вписанной в него, через а, b, с и S.

1) Используем результат задачи 1:

S = Pr, где Р – периметр треугольника, r – радиус вписанной окружности. Р = а + b + с; 2S = r (а + b + c), отсюда:

2) Радиус R описанной окружности вычисляется по формуле: R = , где  – угол, противолежащий стороне а.

Из формулы: S = bc · sin  получим sin  = , тогда 2sin  = . Следовательно, R = .

3. Решить задачу № 1099 на доске и в тетрадях.

Диагонали А3А7 и А4А8 четырехугольника А3А4А7А8 являются диаметрами окружности, в которую вписан данный восьмиугольник, поэтому они равны и точкой пересечения О делятся пополам. Следовательно, четырехугольник А3А4А7А8 – прямоугольник. Так как угол А3ОА4 = 45°, то согласно задаче 1059 площадь прямоугольника равна R2.

4. Решить задачу № 1105 (в) (объясняет учитель).

Пусть АВС – данный треугольник, угол С = 90°, угол В = , АВ = с, ВС = а, СА = b; Р = а + b + с, r – радиус вписанной окружности. Тогда а = с · cos , b = c · sin .

Воспользуемся двумя формулами для вычисления площади S треугольника АВС (метод площадей):

. Отсюда, получаем, r = , поэтому C = 2πr = .

Умножив числитель и знаменатель дроби на cos  + sin  – 1, после несложных преобразований получаем: c = πc (sin  + cos  – 1).

5. Решить задачу № 1117 (в).

Применим метод площадей, то есть воспользуемся двумя формулами для вычисления площади треугольника:

S = ab sin  и S = Pr, где а и b – длины сторон треугольника,  – угол между ними, Р – периметр, r – радиус вписанной окружности. Получим: S = a2 sin  и S = r · а .

Отсюда находим r, а затем площадь круга: Sкруга = .

6. Решить задачи № 1110, 1138, 1116 (в).

Примечание. решения некоторых из них полезно предварительно обсудить, а затем записать в тетрадях, остальные задачи учащиеся могут решить самостоятельно с последующей проверкой ответов или решений.

III. Проверочная самостоятельная работа.

Решить задачи №№ 1125, 1129 (в), 1132 (а), 1134 (а).

Решить задачи №№ 1128, 1129 (г), 1132 (б), 1134 (б).

IV. Итоги уроков.

Домашнее задание: подготовиться к контрольной работе, повторив материал пунктов 105–112 и ответив на вопросы 1–12, с. 290 учебника; решить задачи №№ 1104 (г, д), 1105 (б), 1116 (в).

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

Содержание

Задача: определить площадь круга, если известна длина окружности
Условие задачи:
Найти площадь круга: S
Ответ:
Длина окружности и площадь круга
Просмотр содержимого документа «Длина окружности и площадь круга»
📺 Видео

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Задача: определить площадь круга, если известна длина окружности

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Условие задачи:

Длина окружности 5 м. Найти площадь круга, ограниченного этой окружностью.

Дано:
Длина окружности, L = 5 м

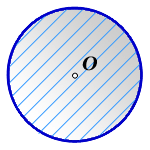
Пояснение к рисунку:
O — центр окружности

Видео:Площадь круга. Математика 6 класс.Скачать

Найти площадь круга: S

Используем формулу площади круга через радиус. Но нам пока не известен радиус, его надо найти.

Определить радиус, нам поможет формула длины окружности.

После преобразования, выразим радиус через длину окружности и подставим значения.

Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14

Получили значение радиуса окружности.

В формулу площади круга, подставляем найденное значение радиуса.

Видео:Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Ответ:

Если в формулу площади круга подставить выраженный радиус через длину окружности, то получим следующую формулу, в которой площадь круга сразу выражена через длину окружности. Проверим, подставив наше значение

Видео:КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Длина окружности и площадь круга

В презентации наглядно изложен материал §2 главы XII учебника Геометрия 7-9 Л.С.Атанасяна. Выведены формулы длины окружности и площади круга, длины дуги, площади сектора и сегментов, рассмотрены задачи по данной теме.

Просмотр содержимого документа
«Длина окружности и площадь круга»

Длина окружности и площадь круга

Автор – Софронова Наталия Андреевна, учитель математики МОУ «Упшинская основная общеобразовательая школа»

К учебнику «Геометрия 7-9» под редакцией Атанасяна

С 1 — длина первой окружности радиуса R 1

Р 1 – периметр вписанного в нее правильного

n-угольника со стороной а 1

С 2 — длина второй окружности радиуса R 2

Р 2 – периметр вписанного в нее правильного

n-угольника со стороной а 2

Найти длину окружности, радиус которой равен 10 см

Найти радиус окружности, длина которой равна 10 см

Длина дуги окружности в α 0 .

Найти длину дуги окружности, градусная мера которой 72 0 , если радиус окружности равен 3 см.

Найти градусную меру угла, соответствующего дуге, длина которой 10 см, если радиус окружности равен 5 см.

Найти радиус окружности, если длина ее дуги в 40 0 равна 8 см.

Длина хорды, стягивающей дугу в α 0 .

1 способ: По теореме косинусов

Найти длину хорды АВ окружности, стягивающей дугу в 140 0 , если радиус окружности равен 3 см.

Дан круг радиуса R, его площадь равна S

Впишем в него правильный n-угольник . Площадь n-угольника равна S n

Впишем в правильный n-угольник окружность радиуса r . Площадь этой окружности равна S /

Найти площадь круга радиуса 5 см.

Найти радиус круга, если его площадь равна 10 см 2

Площадь круга равна m. Найти длину ограничивающей его окружности.

Длина окружности равна m. Найти площадь круга, ограниченного этой окружностью

Найти площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13 см и 12 см .

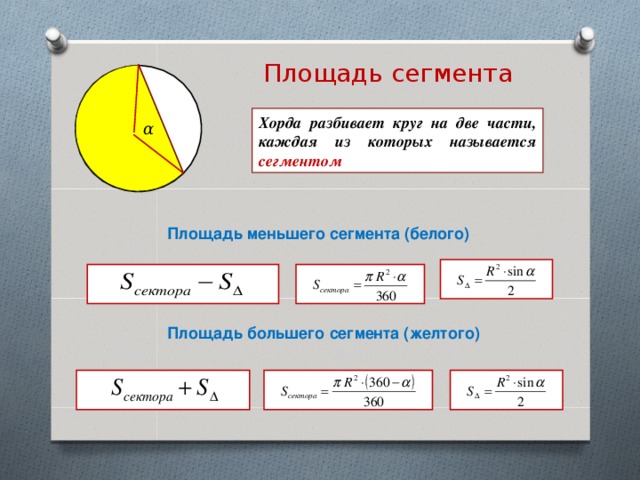
Площадь кругового сектора

Часть круга, ограниченная двумя радиусами и дугой, называется сектором

Найдите площадь кругового сектора радиуса 4 см, если его центральный угол равен 45 0 .

Площадь кругового сектора равна 18π, а его центральный угол равен 40 0 . Найдите радиус сектора.

Сторона правильного шестиугольника равна 1 см. Найдите длину описанной около шестиугольника окружности и площадь ограниченного этой окружностью круга.