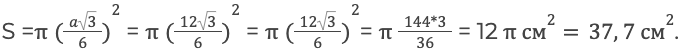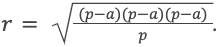Площадь круга внутри треугольника

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Площадь круга. Площадь круга вписанного в треугольник и квадрат (описанного около).

Скачайте удобный калькулятор — любые вычисления,
проценты, расчет по формулам, запись и печать результатов

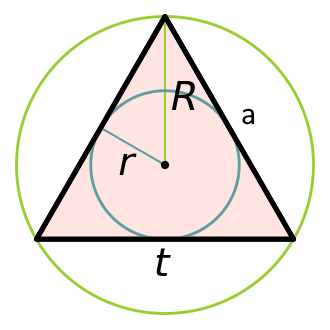
Обозначения:
A, B, C — углы,
a, b, c — стороны,
h — высота,
R — радиус,
S — площадь.
p — полупериметр.

Скачайте удобный калькулятор — любые вычисления,
проценты, расчет по формулам, запись и печать результатов

1. Площадь круга

Где S — площадь круга, R — радиус круга.

2. Площадь круга вписанного в квадрат.

Где a/2 — радиус круга, a — длина стороны квадрата.

3. Площадь круга описанного около квадрата.

Где a — длина стороны квадрата.

В этом случае радиус круга равен 0.5*a*√‾2, используя формулу 1, получаем формулу 3.

4. Площадь круга вписанного в треугольник.

Используя формулу радиуса вписанной окружности
R = (p-a)*tg(A/2)

Где a, A — сторона и противолежащий угол соответственно, p — полупериметр.

Можем записать формулу площади круга вписанного в треугольник:
S = пи * ((p-a)*tg(A/2))²

5. Площадь круга описанного около треугольника.

Используя формулу радиуса описанной окружности
R = a/(2*sin(A))

Где a, A — сторона и противолежащий угол соответственно.

Можем записать формулу площади круга описанного около треугольника:
S = пи * (a/(2*sin(A)))²

6. Формулы полезные в жизни

Часто возникают задачи пересчета объема в площадь или в длину и обратная задача — пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Площадь круга, вписанного в равносторонний треугольник: решение

Содержание:

В геометрии встречаются понятия описанной и вписанной геометрических фигур. Описанным будет треугольник, через вершины которого проходит окружность, вписанным – если его стороны соприкасаются с кругом. Такое построение в обоих случаях обладает рядом особенностей, которые применяются на практике и упрощают решение задач. Рассмотрим свойства и формулы для расчёта описанного 3-угольника.

Видео:Площадь круга. Математика 6 класс.Скачать

Особенности явления

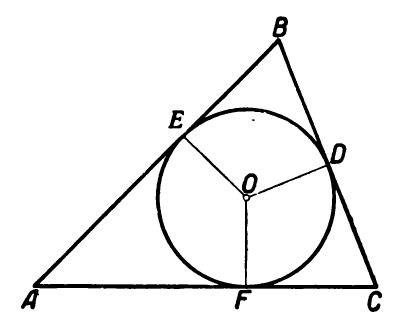
Окружность с центром O, проходящая через одну из точек: D, E либо F обязательно будет лежать и на двух остальных. Прямые, разделяющие углы пополам, или биссектрисы равностороннего треугольника пересекаются в общей точке – центре вписанной окружности, который находится на одинаковом удалении от сторон геометрической фигуры.

Из вышесказанного следуют свойства:

• В треугольник вписывается лишь один круг.
• Его центр находится на одинаковом расстоянии от ближайших точек на сторонах 3-угольника.
• Перпендикуляры, опущенные из центра O, и биссектрисы пересекаются в одной точке, называемой центром вписанной окружности.

Видео:Площадь круга. 9 класс.Скачать

Способ вычислить площадь круга, вписанного в треугольник

Для вычисления площади, если дан только размер стороны правильного треугольника, применяется ряд формул.
S=πr 2 .

a, где:

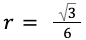
• a – длина стороны геометрической фигуры;
• r – радиус круга, расположенного внутри многоугольника с тремя равными сторонами.

После подстановки значения получается выражение для вычисления площади вписанной окружности:

.

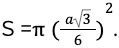
В задачах могут давать длину сторон, тогда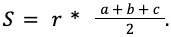
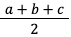
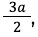
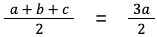
Выражение для равностороннего треугольника можно записать в виде так как 3-угольник равносторонний. С иной стороны – это полупериметр рассматриваемой геометрической фигуры – p.

Зная это, формула записывается в виде: S = r * p.

Видео:Площадь круга. Практическая часть - решение задачи. 6 класс.Скачать

Задачи

В формулу подставим длину сторон треугольника, после вычислений получим результат.

Вычислить занимаемое вписанным в 3-угольник кругом пространство, если его сторона равна 10 см.

Для вычислений необходимо найти радиус r.

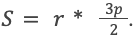
Известно, что он определяется по формуле:

После преобразований выражение упрощается до .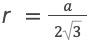

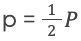
– полупериметр.

Начинаем проводить вычисления.

P = a + a + a = 10 +10 +10 или 10 * 3 = 30 см.

Видео:Площадь кругаСкачать

Треугольник вписанный в окружность

Видео:Лучший способ найти площадь кругаСкачать

Определение

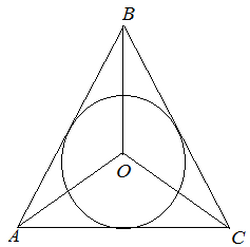
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:№1117. Найдите площадь круга, вписанного: а) в равносторонний треугольник со стороной а;Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Только для гениев. Геометрия квадрата, круга и треугольника. #математика #геометрия #площадь #кругСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

📹 Видео

КАК НАЙТИ ПЛОЩАДЬ КРУГА, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР? Примеры | МАТЕМАТИКА 6 классСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Олимпиадная геометрия ➜ Найдите площадь круга внутри квадратаСкачать

Урок 8. Вычисление площадей треугольнико четырехугольников. Площадь круга | МатематикаСкачать

Длина окружности. Площадь круга, 6 классСкачать

Найти площадь круга.Скачать

Как найти площадь круга?Скачать

КАК НАЙТИ ПЛОЩАДЬ КРУГА, ОПИСАННОГО ОКОЛО КВАДРАТА? Примеры | ГЕОМЕТРИЯ 9 классСкачать

Найдите площадь кругаСкачать

Площадь круга - Доказательство Архимеда πR²Скачать