Площадь и периметр ромба с вписанной окружностью (2 видео)

Ромб. Формулы, признаки и свойства ромба


Рис.1	Рис.2

Содержание

Признаки ромба
Основные свойства ромба
Сторона ромба
Формулы определения длины стороны ромба:
Диагонали ромба
Формулы определения длины диагонали ромба:
Периметр ромба
Формула определения длины периметра ромба:
Площадь ромба
Формулы определения площади ромба:
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
Площадь и периметр ромба с вписанной окружностью
Контакты
Ромб, свойства, признаки, формулы, площадь и периметр
Примеры решения задач
Видео
Площадь ромба
Формулы определения площади ромба:
Сторона ромба
Формулы определения длины стороны ромба:
Основные соотношения
Периметр и площадь
Нахождение стороны
Другие соотношения
Видео

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

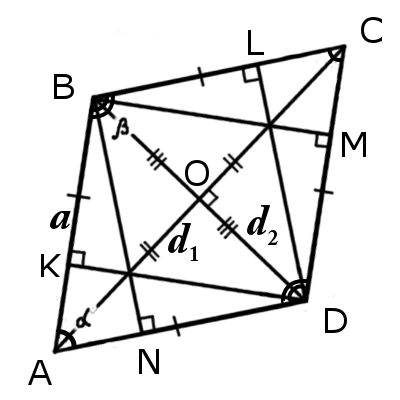
Признаки ромба

∠BAC = ∠CAD или ∠BDA = ∠BDC

Δ ABO = Δ BCO = Δ CDO = Δ ADO

Видео:Задача 6 №27914 ЕГЭ по математике. Урок 132Скачать

Основные свойства ромба

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

AC 2 + BD 2 = 4AB 2

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:

a =	S
	h_a

2. Формула стороны ромба через площадь и синус угла:

a =	√ S
	√ sinα

a =	√ S
	√ sinβ

3. Формула стороны ромба через площадь и радиус вписанной окружности:

a =	S
	2 r

4. Формула стороны ромба через две диагонали:

a =	√ d ₁ 2 + d ₂ 2
	2

5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):

a =	d ₁
	√ 2 + 2 cosα

a =	d ₂
	√ 2 — 2 cosβ

6. Формула стороны ромба через большую диагональ и половинный угол:

a =	d ₁
	2 cos ( α /2)

a =	d ₁
	2 sin ( β /2)

7. Формула стороны ромба через малую диагональ и половинный угол:

a =	d ₂
	2 cos ( β /2)

a =	d ₂
	2 sin ( α /2)

8. Формула стороны ромба через периметр:

a =	Р
	4

Видео:Радиус вписанной в ромб окружности (6701)Скачать

Диагонали ромба

Формулы определения длины диагонали ромба:

d ₁ = a √ 2 + 2 · cosα

d ₁ = a √ 2 — 2 · cosβ

d ₂ = a √ 2 + 2 · cosβ

d ₂ = a √ 2 — 2 · cosα

d ₁ = 2 a · cos ( α /2)

d ₁ = 2 a · sin ( β /2)

d ₂ = 2 a · sin ( α /2)

d ₂ = 2 a · cos ( β /2)

7. Формулы диагоналей через площадь и другую диагональ:

d ₁ =	2S
	d ₂

d ₂ =	2S
	d ₁

8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

d ₁ =	2 r
	sin ( α /2)

d ₂ =	2 r
	sin ( β /2)

Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Периметр ромба

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можно найти за формулами указанными выше.

Формула определения длины периметра ромба:

Видео:№493. Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.Скачать

Площадь ромба

Формулы определения площади ромба:

4. Формула площади ромба через две диагонали:

S =	1	d ₁ d ₂
	2

5. Формула площади ромба через синус угла и радиус вписанной окружности:

S =	4 r 2
	sinα

6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):

S =	1	d ₁ 2 · tg ( α /2)
	2

S =	1	d ₂ 2 · tg ( β /2)
	2

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

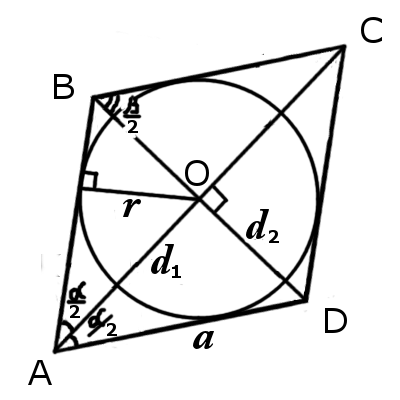
Окружность вписанная в ромб

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

r =	h
	2

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

r =	S
	2 a

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

r =	√ S · sinα
	2

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

r =	a · sinα
	2

r =	a · sinβ
	2

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

r =	d ₁ · sin ( α /2)
	2

r =	d ₂ · sin ( β /2)
	2

6. Формула радиуса круга вписанного в ромб через две диагонали:

r =	d ₁ · d ₂
	2√ d ₁ 2 + d ₂ 2

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

r =	d ₁ · d ₂
	4 a

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

Площадь и периметр ромба с вписанной окружностью

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Ромб, свойства, признаки, формулы, площадь и периметр

Видео:Геометрия Найдите периметр ромба, диагонали которого равны 24 см и 32 смСкачать

Примеры решения задач

Дано: ABCD — ромб. AC=24 ; BD=10 Найти: AB=? Решение: Составим уравнение исходя из третьего свойства ромба. AC2+BD2=4AB2 576+100=4AB2 676=4AB2 AB=6.5 Ответ: длина стороны AB=6.5

Дано: ABCD—ромб;∠A+∠C=120°;PABCD=68 Найти: BD = ? Решение: 1 способ — P=68=>AB=68:4=17=>AB=BC=DC=AD=17; 2 способ — ∠A=∠D (по свойствам ромба) ; ∠A=∠C=120:2=60° ∠B=∠D (по свойствам ромба) ; ∠B=∠D=(360-120):2=120° ▵ABO — прямоугольный (т.к. диагонали в ромбе пересекаются под прямым углом) ∠BAO=30° (т.к. диагонали в ромбе являются его биссектрисами) =>BO=8.5(т.к. сторона в прямоугольном треугольнике, лежащая напротив угла 30°, равна половине гипотенузы) BD=8.5×2=17 Ответ: длина стороны BD=17

Видео:Периметр ромба равен 180, а один из углов равен 30° | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Видео

Видео:Геометрия. Параллелограмм. Часть 3. Площадь и периметр.Скачать

Площадь ромба

Формулы определения площади ромба:

2. Формула площади ромба через сторону и синус любого угла:

4. Формула площади ромба через две диагонали:

Площадь и периметр ромба с вписанной окружностью

S =	1	d ₁ d ₂
2

5. Формула площади ромба через синус угла и радиус вписанной окружности:

S =	4 r 2
sinα

6. Формулы площади через большую диагональ и тангенс острого угла (tgα ) или малую диагональ и тангенс тупого угла (tgβ ): S = 1d 12 · tg (α /2)2 S = 1d 22 · tg (β /2)2

Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:

a =	S
h_a

2. Формула стороны ромба через площадь и синус угла:

a =	√ S
√ sinα

a =	√ S
√ sinβ

3. Формула стороны ромба через площадь и радиус вписанной окружности:

a =	S
2 r

4. Формула стороны ромба через две диагонали:

a =	√ d ₁ 2 + d ₂ 2
2

5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):

a =	d ₁
√ 2 + 2 cosα

a =	d ₂
√ 2 — 2 cosβ

6. Формула стороны ромба через большую диагональ и половинный угол:

a =	d ₁
2 cos ( α /2)

a =	d ₁
2 sin ( β /2)

7. Формула стороны ромба через малую диагональ и половинный угол:

a =	d ₂
2 cos ( β /2)

a =	d ₂
2 sin ( α /2)

8. Формула стороны ромба через периметр: a = Р4

Видео:ОКРУЖНОСТЬ (радиус окружности, вписанной в ромб) ЧАСТЬ 11Скачать

Основные соотношения

Для решения задач применяются формулы. Ромб не является исключением. Соотношения применяются для определения неизвестных параметров фигуры. Однако бывают случаи, когда недостаточно одной формулы, поскольку нужно связать несколько компонентов в единый процесс вычислений. Для корректного использования формул следует ввести класс некоторых обозначений:

Ромб обозначить набором латинских букв ABCD.
Стороны приравнять к некоторому числу, заданному в общей форме: AB = BC = CD = DA = a.
Диагонали: меньшая — m2 и большая = m1. Их точку пересечения следует обозначить литерой P.
Углы: ∠ABC = ∠ADC и ∠BAD = ∠BCD.
Характеристики вписанной окружности: диаметр D и радиус R.
Периметр и площадь (размерность): P и S соответственно.

Периметр и площадь

Периметр ромба — характеристика, которая эквивалентна значению алгебраической суммы всех ее сторон. Площадью называется параметр геометрической фигуры, показывающий ее размерность в определенном геометрическом пространстве. Следует отметить, что величина S существует только у фигуры в двумерном пространстве. В трехмерном нужно рассматривать объем геометрического тела. Кроме того, у объемного тела есть параметр площади поперечного сечения. Эта величина является двумерной.

Периметр вычисляется по следующей формуле: P = 4 * a. Следует отметить, что величину a можно выражать через диагонали, площадь и другие характеристики. Базовая формула площади ромба имеет такой вид: S = a * BP = a * DP = a * AP = a * CP. Кроме того, размерность можно найти по следующим соотношениям:

S = a 2 * sin (∠ABC) = a 2 * sin (∠BCD) (через синус острого угла).
S = 2 * a * R.
S = (m1 * m2) / 2.
S = (4 * R 2 ) / sin (∠BAD).
S = [(m1)^2 * tg (∠BAD / 2)] / 2 = [(m2)^2 * tg (∠ABC / 2)] / 2.

В последней формуле при большем значении диагонали m1 следует брать тангенс острого угла, а при m2 — тангенс тупого угла. На это нужно обратить особое внимание, поскольку на этом моменте новички делают много ошибок, путая диагонали и углы.

Нахождение стороны

Длина стороны находится очень просто, поскольку математики выполнили доказательства некоторых тождеств. Они предлагают готовые решения в виде формул, позволяющих правильно выразить одну величину через другую, и подставить необходимые числовые значения:

a = S / BP = S / DP = S / AP = S / CP.
a = S^(½) / (sin (∠BAD))^(½).
a = S / 2 * R.
a = [(m1)^2 + (m2)^2]^(½) / 2.
a = P / 4.

Необходимо обратить внимание, что используются в некоторых соотношения тригонометрические функции. Последнее соотношение является формулой определения периметра. Если он известен, то легко вычислить значение стороны, используя обратную формулу P.

Другие соотношения

Осталось еще два параметра ромба — диагонали. Специалисты рекомендуют воспользоваться готовыми соотношениями для нахождения ее длины:

m1 = 2 * a * cos (∠BAD/2).
m2 = 2 * a * sin (∠BAD/2).

m1 = [4 * a 2 — (m2)^2]^(½) = [4 * S — (m2)^2]^(½).

m2 = [4 * a 2 — (m1)^2]^(½) = [4 * S — (m1)^2]^(½).

Следует также рассмотреть случай, когда окружность вписана в ромб. Такой прием применяется для расширения возможностей поиска неизвестной, что существенно позволит сэкономить время на расчетах. К формулам относятся следующие тождества:

R = S / 2 * a.
R = m1 * m2 / (2 * ((m1)^2 + (m2)^2)^(½)).
R = m1 * m2 / P = m1 * m2 / 4 * a.

Если нужно найти диаметр, то следует использовать такое соотношение: R = D / 2. Можно также выразить диагонали через стороны. Для этого следует подставить вместо m1 значение со стороной a.

Таким образом, математики предлагают специальный алгоритм, позволяющие без ошибок идентифицировать ромб, а затем применить соответствующие формулы для решения задачи.