Пирамида с вырезом треугольника

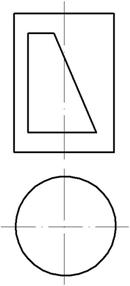
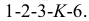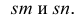Пример 1. Построить три проекции цилиндра с вырезом (рис. 147).

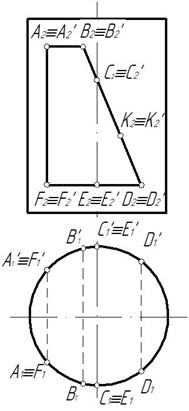
Отмечаем характерные точки выреза А, В, С, Д, Е, F, а также произвольную точку к для построения профильной проекции части эллипса. Горизонтальные проекции точек отмечаем на горизонтальном очерке цилиндра, так как горизонтальная проекция боковой поверхности цилиндра совпадает с горизонтальным очерком (рис .148)

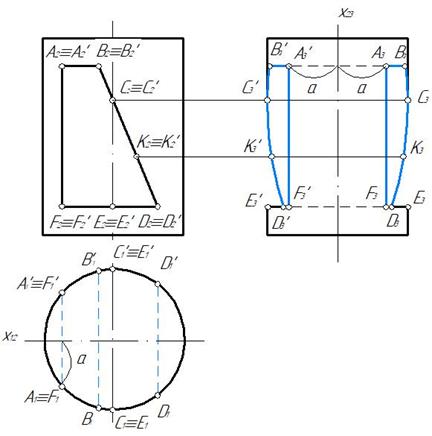
Построение профильной проекции выреза показано на рис. 149. Для этого целесообразно ось x ₁₂ провести через ось симметрии горизонтальной проекции,а ось x ₂₃ через профильную ось симметрии.

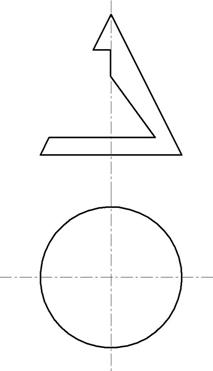
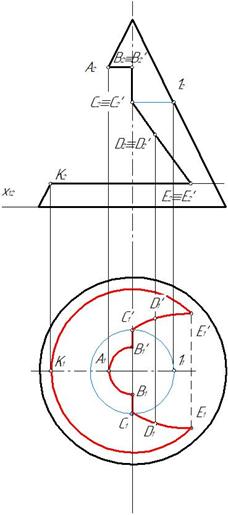
Пример 2. Построить три проекции конуса с вырезом (рис. 150).

Отмечаем характерные точки вареза А, В, С, Е, K, а также произвольную точку D для построения части эллипса. Горизонтальные проекции точек отмечаем на образующих конуса и вспомогательных окружностях (рис. 151).

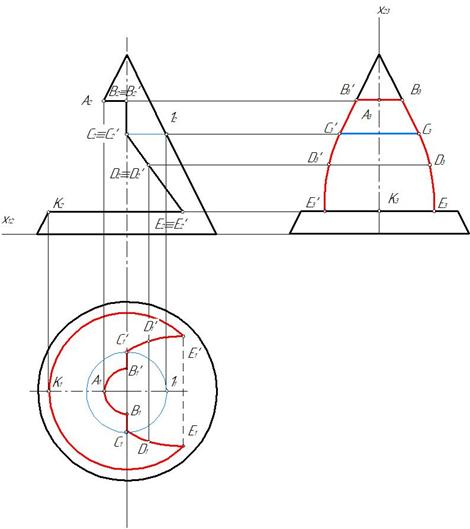
На рис. 152 показано построение профильной проекции конуса с вырезом.Для этого целесообразно ось x ₁₂ провести через ось симметрии горизонтальной проекции, а ось x ₂₃ через профильную ось симметрии.

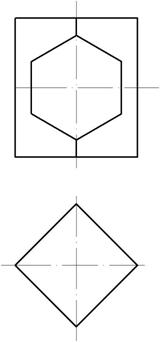
Пример 3. Построить три проекции вырезе на призме (рис. 153).

Решение показано на рис. 154

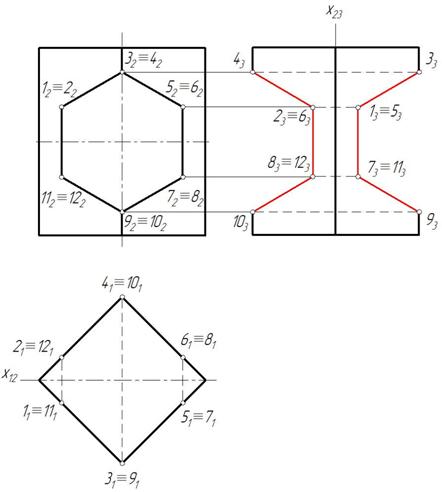
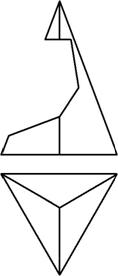
Пример 4. Построить три проекции выреза на пирамиде (рис. 155).

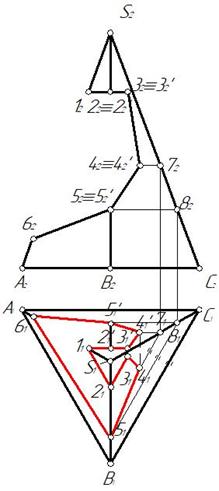
Отмечаем фронтальные проекции характерных точек выреза – это точки 1₂, 2₂, 3₂, 4₂, 5₂, 6₂. Для нахождения горизонтальных проекций точек 4 и 5 проводим по поверхности пирамиды две вспомогательные линии, параллельные основанию пирамиды ABC. Горизонтальные проекции этих линий являются треугольниками, параллельными горизонтальной проекции основания А₁В₁С₁. На этих треугольниках отмечаем горизонтальные проекции точек 4 и 5 (рис. 156).

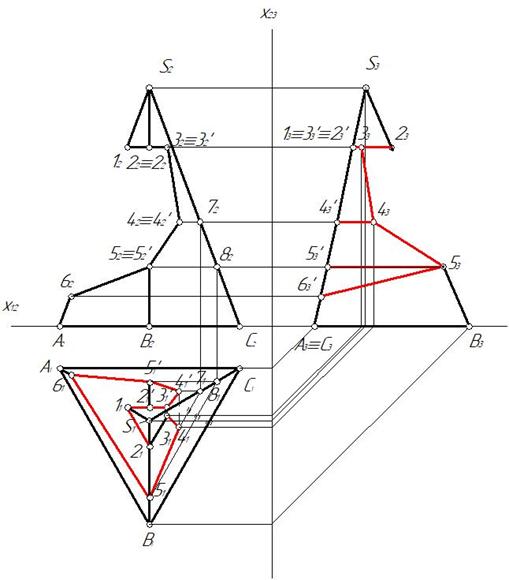
Затем строим профильную проекцию пирамиды и точек выреза. Для этого оси целесообразно провести как показано на рис. 157.

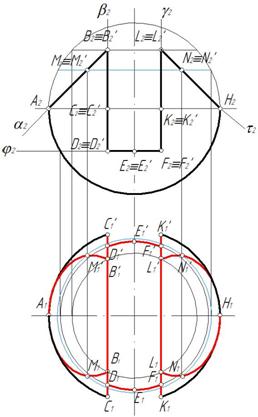
Пример 5. Построить три проекции выреза на сфере (рис. 158).

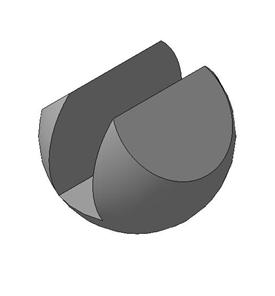
Вырез образован двумя фронтально-проецирующими плоскостями α и τ, горизонтальной плоскостью φ, двумя профильными плоскостями β и γ. Горизонтальная плоскость пересекает поверхность сферы по части окружности, ограниченной прямой. Фронтально-проецирующая плоскость пересекают поверхность сферы по окрухностям, которые на горизонтальной и профильной плоскости проецируются как части эллипсов. Профильная плоскость пересечет поверхность сферы по части окружности, которая на профильной плоскости спроецируется как часть окружности (рис. 159).

Построение профильной проекции показано на рис. 160

Видео:Пирамида с вырезомСкачать

Лекция 6. Многогранники

Видео:Лекция 5 Задача 4Скачать

6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды

Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.

Грани, пересекаясь, образуют ребра .
Ребра, пересекаясь, образуют вершины .
Рассмотрим два основных вида многогранников:

Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.

Видео:Пересечение многогранников. Пирамида с призматическим вырезом.Скачать

Упражнение

Дана пирамида, основание которой параллельно π₁. Основание представляет собой некоторый треугольник.

S – вершина пирамиды (Рисунок 6.1).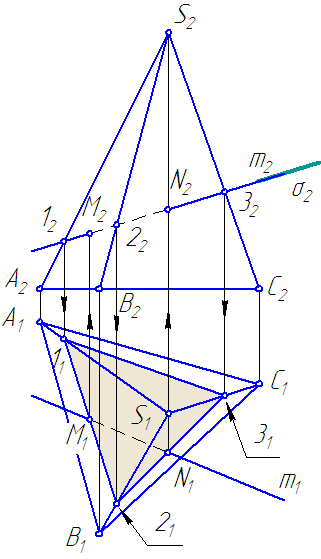

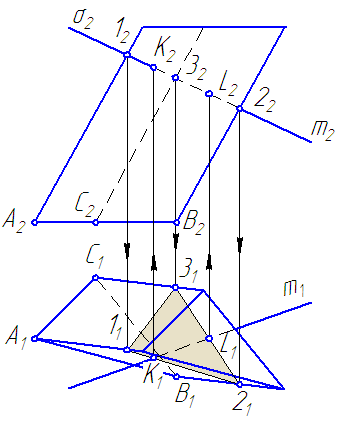
Рисунок 6.1 – Пересечение поверхности пирамиды прямой

Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.

1. Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
2. Строим сечение ∆ (123) поверхности пирамиды с плоскостью σ.

Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость σ).

Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции необходимо выполнять при помощи пропорционального деления отрезка.

1. В сечении находим точки M и N принадлежащие прямой m.
2. Определяем видимость прямой m.

Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.

Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.

Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.

Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).

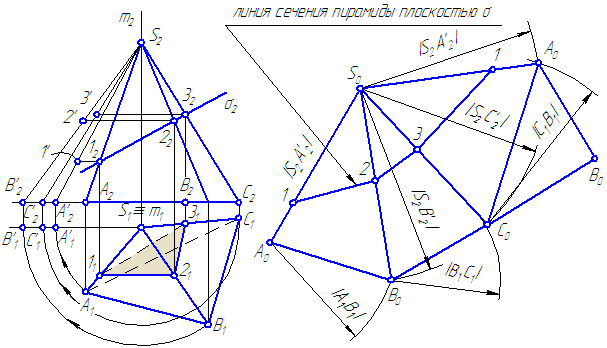
Рисунок 6.2 – Построение развёртки пирамиды

В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки overline,overline,overline , проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.

Видео:ПИРАМИДА в ИЗОМЕТРИИСкачать

6.2. Призма. Развертка призмы

Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.

Видео:Развертка пирамидыСкачать

Упражнение

Дана призма, основания которой параллельны плоскости проекций π₁.

Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).

Рисунок 6.3 – Построение «точек встречи» прямой с поверхностью наклонной призмы

1. Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
2. Строим сечение поверхности призмы с плоскостью σ →(∆(123)).
3. В сечении находим точки K и L принадлежащие прямой m.
4. Определяем видимость прямой m. Если грань АВ на π₂ видна, то точка К на π₂ видима, грань ВС невидима, следовательно, точка Lневидима.

Рассмотрим наклонную призму. Пусть основание призмы параллельно π₁, а ребра параллельны π₂.

Построим нормальное сечение, то есть сечение плоскостью σ, перпендикулярной ребрам призмы (Рисунок 6.4).

Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.

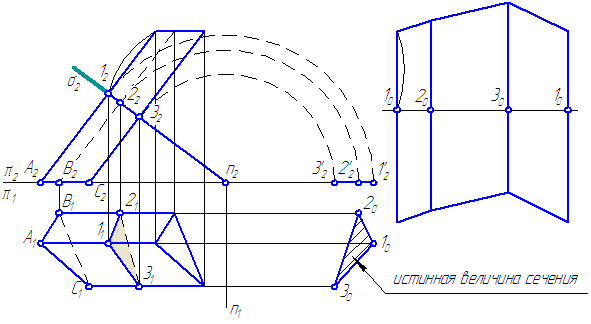
Рисунок 6.4 – Построение развёртки призмы
Порядок построения :

1. Найдем истинную величину сечения – (1₀2₀3₀), для чего повернём сечение (123) вокруг оси n⊥π₂, (можно ввести ДПП π₃//σ).
2. Проведём горизонтальную линию на свободном месте листа. Отложим на ней отрезки:
   /1₀-2₀/; /2₀-3₀/; /3₀-1₀/.

1. Проведём направления рёбер перпендикулярно этой линии через точки: 1₀; 2₀; 3₀ и отмерим вверх и вниз расстояния от нормального сечения (на π₂) до верхнего и нижнего основания, откладывая их на линиях-ребрах.

Видео:Лекция 4. Многогранники. Часть 4.Скачать

6.3. Взаимное пересечение многогранников

В результате пересечения многогранников получим ломаную линию.

Возможны два случая пересечения многогранников (Рисунок 6.5):

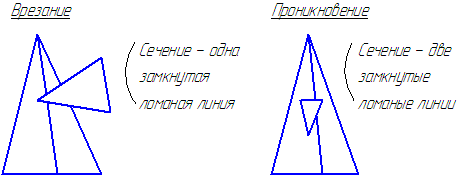
Рисунок 6.5 – Варианты пересечения многогранников

Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.

Звенья ломаной – линии пересечения граней.

Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.

Построенные точки соединить.

Видео:Треугольная пирамида. Проекции точек на гранях. Сечение. Урок23.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Упражнение

Построить линии пересечения призмы с пирамидой (Рисунок 6.6).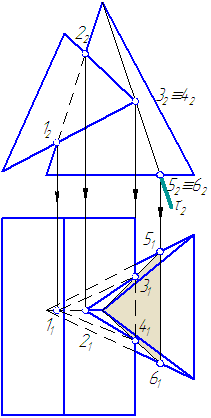

Рисунок 6.6. Построение линии пересечения призмы с пирамидой
Решение

1. Находим на π₂ проекции точек пересечения ребра пирамиды с проецирующими гранями призмы (точки 1₂ и 2₂). Находим их горизонтальные проекции.
2. Строим точки пересечения ребра призмы с боковыми гранями пирамиды (точки 3₂ и 4₂), для чего используем вспомогательную плоскость τ⊥π₂.
3. Полученные на π₁ точки 3, 2, 4, 1 соединяем отрезками прямых. Причем отрезки 1₁-3₁, 1₁-2₁, 1₁-4₁ невидимы. Получили замкнутую линию пересечения пирамиды с призмой.

Видео:Как начертить КОНУС С ВЫРЕЗОМ (чертеж + аксонометрия)Скачать

Упражнение

остроить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).

1. По двум проекциям построить третью;
2. На всех трех проекциях построить проекции линии пересечения призматического выреза с пирамидой;
3. Невидимые участки линии пересечения и участки рёбер многогранников показывать штриховой линией;
4. Построить развёртку пирамиды с нанесением линии пересечения.

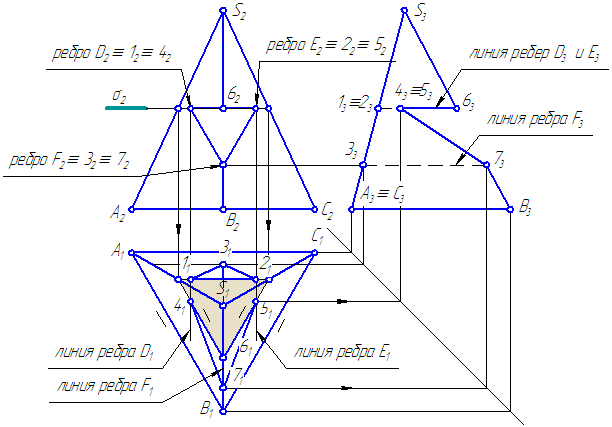
Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки
Решение :

1. Проводим линии рёбер призмы на всех проекциях.
2. Введём плоскость σ⊥π₂, σ//π₁:

• σ//АВС – основанию пирамиды;
• σ пересекает пирамиду ’ сечение подобно ΔА₁В₁С₁.

Это сечение пересекается:

— с ребром D в двух точках 1 и 4;

— с ребром Е в двух точках 2 и 5.

Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.

Построение развертки рассмотрено ранее.

Видео:Я СДЕЛАЛ СВОЙ ДОМ ТРЕУГОЛЬНЫМ В МАЙНКРАФТ | Компот MinecraftСкачать

6.4. Задачи для самостоятельной работы

1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).

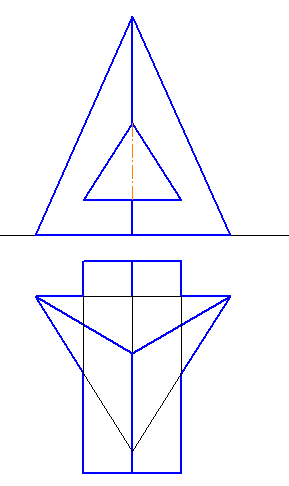
Рисунок 6.8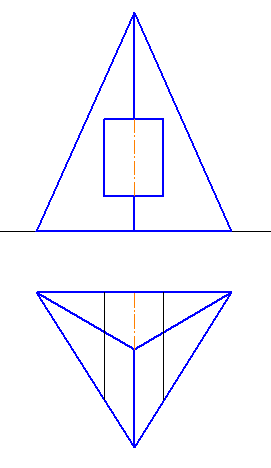

Рисунок 6.9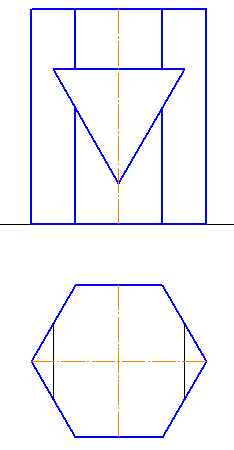

Рисунок 6.10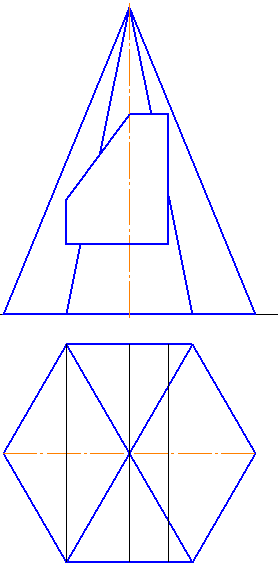

Рисунок 6.11

Видео:1.2 ПИРАМИДА. Геометрические тела.Скачать

Пирамида с вырезом в начертательной геометрии с примером

Пирамида с вырезом:

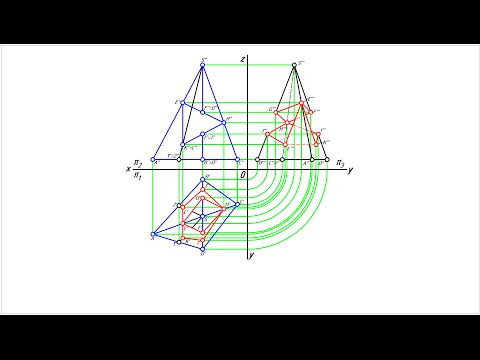
В качестве примера построения сечений многогранника несколькими плоскостями рассмотрим построение пирамиды с вырезом. Вырез образован тремя плоскостями —

Плоскость Р параллельна горизонтальной плоскости проекций. Она пересекает поверхность пирамиды по пятиугольнику

Фронтально-проецируюшая плоскость R пересекает пирамиду по пятиугольнику 1-2-7-8-9. Чтобы найти горизонтальные проекции точек 8 и 9, проведем через них дополнительные образующие SM и SN, сначала на фронтальной проекции — 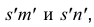а затем на горизонтальной —

Фронтально-проецирующая плоскость Т пересекает пирамиду по пятиугольнику 5-4-8-9-10. Построив горизонтальную проекцию выреза, строим его профильную проекцию.

• Коническая и цилиндрическая поверхности
• Построение проекций линии пересечения цилиндра плоскостью
• Развертка поверхности цилиндра
• Построение проекций линий пересечения конуса плоскостью
• Пересечение многогранников плоскостями
• Развертка поверхности призмы
• Развертка поверхности правильной пирамиды
• Развертка поверхности неправильной пирамиды

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

📹 Видео

Построение проекции пирамиды в трех плоскостях и построение точек 1 и 2, свободно расположенных в ееСкачать

Комплексный чертеж усеченной 5-гранной пирамидыСкачать

Пирамида с призматическим вырезом. КОМПАС-3D.Скачать

Пересечение пирамиды с призмойСкачать

Теория строительства пирамиды ХеопсаСкачать

Построение недостающих проекции сквозного отверстия в сфереСкачать

Интересный гидравлический домкрат. Сибталь LJ.Скачать

Построение линии пересечения поверхности пирамиды с проецирующей плоскостьюСкачать

Конус с вырезомСкачать

Ойығы бар пирамида - ДиметрияСкачать