Пирамида – многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.
По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д.
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
- Некоторые свойства пирамиды
- Виды пирамид
- Геометрические фигуры. Прямоугольная пирамида.
- Свойства пирамиды.
- Формулы для определения объема и площади прямоугольной пирамиды.
- Пирамида основание которой прямоугольный треугольник
- Особые случаи пирамиды
- Правильная пирамида
- Прямоугольная пирамида
- Усечённая пирамида
- 🌟 Видео
Видео:№251. Основанием пирамиды DABC является прямоугольный треугольник с гипотенузой ВС. БоковыеСкачать

Некоторые свойства пирамиды
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Верно и обратное.
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр
Верно и обратное.
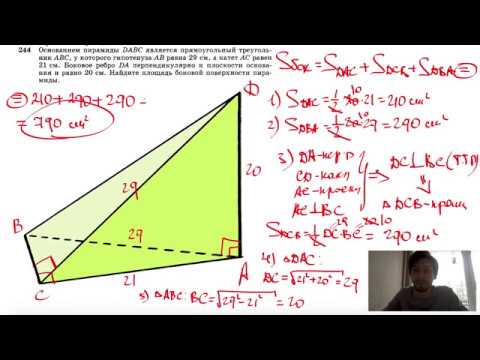
Видео:№244. Основанием пирамиды DABC является прямоугольный треугольник ABC, у которого гипотенузаСкачать
Виды пирамид
Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Видео:Построение проекции пирамиды. Метод прямого треугольника.Скачать

Пирамида называется прямоугольной , если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Видео:Стереометрия на ЕГЭ Найти объём пирамиды, основанием которой является правильный шестиугольникСкачать

Геометрические фигуры. Прямоугольная пирамида.
Прямоугольная пирамида — это пирамида, в которой одно из боковых рёбер перпендикулярно основанию.
В этом случае, это ребро и будет высотой пирамиды.
Видео:🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Свойства пирамиды.
1. Когда все боковые ребра имеют одинаковую величину, тогда:
- около основания пирамиды легко описать окружность, при этом вершина пирамиды будет проецироваться в центр этой окружности;
- боковые ребра образуют с плоскостью основания одинаковые углы;
- кроме того, верно и обратное, т.е. когда боковые ребра образуют с плоскостью основания равные углы, либо когда около основания пирамиды можно описать окружность и вершина пирамиды будет проецироваться в центр этой окружности, значит, все боковые ребра пирамиды имеют одинаковую величину.
2. Когда боковые грани имеют угол наклона к плоскости основания одной величины, тогда:
- около основания пирамиды легко описать окружность, при этом вершина пирамиды будет проецироваться в центр этой окружности;
- высоты боковых граней имеют равную длину;
- площадь боковой поверхности равняется ½ произведения периметра основания на высоту боковой грани.
3. Около пирамиды можно описать сферу в том случае, если в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы станет точка пересечения плоскостей, которые проходят через середины ребер пирамиды перпендикулярно им. Из этой теоремы делаем вывод, что как около всякой треугольной, так и около всякой правильной пирамиды можно описать сферу;
4. В пирамиду можно вписать сферу в том случае, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в 1-ной точке (необходимое и достаточное условие). Эта точка станет центром сферы.
5. Конус будет вписанным в пирамиду, когда вершины их совпадут, а основание конуса будет вписанным в основание пирамиды. При этом вписать конус в пирамиду можно лишь в том случае, если апофемы пирамиды имеют равные величины (необходимое и достаточное условие);
6. Конус будет описанным около пирамиды, если их вершины совпадут, а основание конуса будет описано около основания пирамиды. При этом описать конус около пирамиды можно лишь в том случае, если все боковые ребра пирамиды имеют одинаковые величины (необходимое и достаточное условие). Высоты у этих конусов и пирамид одинаковы.
7. Цилиндр будет вписанным в пирамиду, если 1-но его основание совпадет с окружностью, которая вписана в сечение пирамиды плоскостью, параллельной основанию, а второе основание будет принадлежать основанию пирамиды.
8. Цилиндр будет описанным около пирамиды, когда вершина пирамиды будет принадлежать его одному основанию, а второе основание цилиндра будет описано около основания пирамиды. При этом описать цилиндр около пирамиды можно лишь в том случае, если основанием пирамиды служит вписанный многоугольник (необходимое и достаточное условие).
Видео:Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Формулы для определения объема и площади прямоугольной пирамиды.
V — объем пирамиды,
S — площадь основания пирамиды,
h — высота пирамиды,
Sb — площадь боковой поверхности пирамиды,
a — апофема (не путать с α) пирамиды,
P — периметр основания пирамиды,
n — число сторон основания пирамиды,
b — длина бокового ребра пирамиды,
α — плоский угол при вершине пирамиды.
Видео:№243. Основанием пирамиды DABC является треугольник ABC, у которого АВ = АС= 13 см, ВС=10 см; реброСкачать
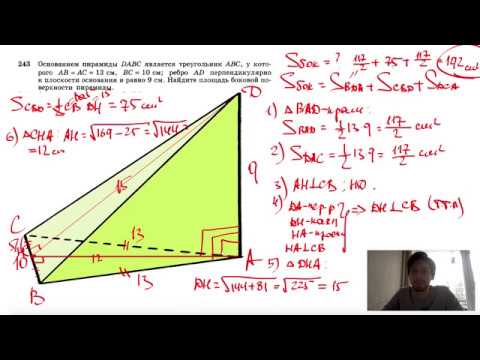
Пирамида основание которой прямоугольный треугольник
Пирамида — (от греч. pyramis, род. п. pyramidos), многогранник,
основание которого многоугольник, а остальные грани треугольники, имеющие
общую вершину. По числу углов основания различают пирамиды треугольные,
четырехугольные и т. д.
Общая вершина боковых граней называется вершиной пирамиды. Высотой
пирамиды называется перпендикуляр, опущенный из вершины пирамиды на
плоскость основания.
– многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса .
Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основани
Если все боковые ребра равны, то:
- около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр;
- боковые ребра образуют с плоскостью основания равные углы.
- также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом, то:
- в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;
- высоты боковых граней равны;
- площадь боковой поверхности равна половине произведения периметра
- Объём пирамиды может быть вычислен по формуле:
где
— площадь основания и
— высота;
- Боковая поверхность — это сумма площадей боковых граней:
- Полная поверхность — это сумма площади боковой поверхности и площади основания:
- Для нахождения боковой поверхности в правильной пирамиде можно использовать формулы:
где
— апофема ,
— периметр основания,
— число сторон основания,
— боковое ребро,
— плоский угол при вершине пирамиды.
Видео:Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать
Особые случаи пирамиды
Правильная пирамида
Пирамида называется правильной, если основанием её является правильный многоугольник , а вершина проецируется в центр основания. Тогда она обладает такими свойствами:
- боковые ребра правильной пирамиды равны;
- в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
- в любую правильную пирамиду можно как вписать, так и описать около неё сферу;
- если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна
, а каждый из них соответственно
, где n — количество сторон многоугольника основания [6] ;
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Прямоугольная пирамида
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.
Усечённая пирамида
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
🌟 Видео
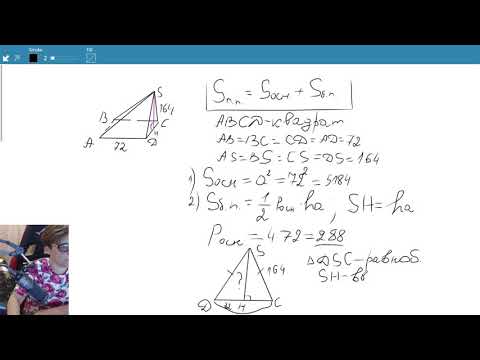
№239. Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналейСкачать
Делаем модель пирамиды для решения задачи по стереометрииСкачать
Трехгранный угол в пирамидеСкачать
10 класс, 32 урок, ПирамидаСкачать
10 класс, 33 урок, Правильная пирамидаСкачать
№234. Основанием прямой призмы является прямоугольный треугольник. Через середину гипотенузыСкачать
🔴 В основании прямой призмы лежит прямоугольный ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать
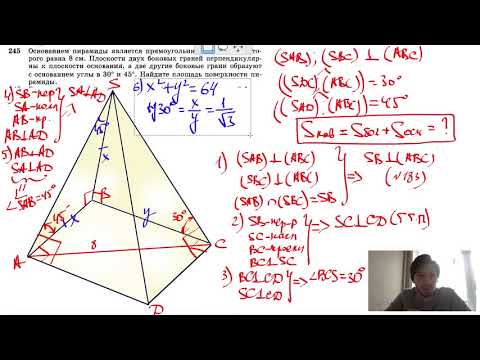
№245. Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. ПлоскостиСкачать
КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать
ВСЕ О ПИРАМИДАХ! ЧАСТЬ II #shorts #егэ #огэ #математика #геометрия #пирамида #профильныйегэСкачать
10 класс — Разбор задач по теме "Пирамида"Скачать
НЕОБЫЧНАЯ ПИРАМИДА / как найти объем? #74895Скачать













 где
где  — площадь основания и
— площадь основания и  — высота;
— высота;

 где
где  — апофема ,
— апофема ,  — периметр основания,
— периметр основания,  — число сторон основания,
— число сторон основания,  — боковое ребро,
— боковое ребро,  — плоский угол при вершине пирамиды.
— плоский угол при вершине пирамиды.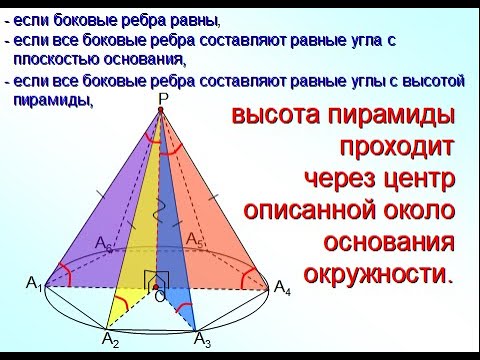
 , а каждый из них соответственно
, а каждый из них соответственно  , где n — количество сторон многоугольника основания [6] ;
, где n — количество сторон многоугольника основания [6] ;