Первая окружность с центром а касается второй

Первая окружность с центром O, вписанная в равнобедренный треугольник KLM, касается боковой стороны KL в точке B, а основания ML — в точке A. Вторая окружность с центром O₁ касается основания ML и продолжений боковых сторон.

а) Докажите, что треугольник OLO₁ прямоугольный.

б) Найдите радиус второй окружности, если известно, что радиус первой равен 15 и AK = 32.

а) Пусть окружность с центром O₁ касается продолжения боковой стороны KL в точке C. Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому LO и LO₁ — биссектрисы смежных углов KLM и CLM. Следовательно, ∠OLO₁ = 90°.

б) Прямоугольные треугольники KBO и KAL подобны, поэтому

Пусть радиус окружности с центром O₁ равен r₁. Треугольник KLM

равнобедренный, поэтому окружности с центрами O и O₁ касаются основания ML в одной и той же точке A. Значит, точка A лежит на отрезке OO₁, причём LA — высота прямоугольного треугольника OLO₁, проведённая из вершины прямого угла. Следовательно,

Видео:Окружность с центром на стороне AС треугольника ABC проходит через вершину С и касается прямой AB вСкачать

Первая окружность с центром а касается второй

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Разделы

Видео:Касательные к окружности с центром O в точках A и B ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Дополнительно

Задача по математике — 6823

На стороне $AB$ выпуклого четырёхугольника $ABCD$ отмечены точки $E$ и $F$, на стороне $BC$ — точки $K$ и $L$, на стороне $CD$ — точки $M$ и $N$, на стороне $AD$ — точки $P$ и $Q$. При этом $AE=EF=FB$, $BK=KL=LC$, $CM=MN=ND$ и $DP=PQ=QA$.
а) Докажите, что отрезки $KQ$ и $LP$ делят отрезок $FM$ на три равных отрезка.
б) Известно, что площадь четырёхугольника $ABCD$ равна 18. Найдите площадь четырёхугольника, вершины которого — точки пересечения прямых $EN$, $FM$, $KQ$ и $LP$.

Задача по математике — 6824

Общие внутренние касательные к двум окружностям перпендикулярны. Одна из них касается окружностей в точках $A$ и $C$, вторая — в точках $B$ и $D$ (точки $A$ и $B$ лежат на одной окружности).
а) Докажите, что отрезок $AC$ равен сумме радиусов окружностей.
б) Найдите площадь четырёхугольника $ABCD$, если известно, что $AB=6$, $CD=8$.

Задача по математике — 6825

Окружность с центром $O$ касается боковой стороны $AB$ равнобедренного треугольника $ABC$, продолжения боковой стороны $AC$ и продолжения основания $BC$ в точке $N$. Точка $M$ — середина основания $BC$.
а) Докажите, что $AN=OM$.
б) Найдите $OM$, если стороны треугольника $ABC$ равны 10, 10 и 12.

Задача по математике — 6826

Окружность с центром $O$, вписанная в треугольник $ABC$, касается стороны $BC$ в точке $M$. Окружность с центром $O_$ касается стороны $BC$ в точке $N$, а также касается продолжений сторон $AC$ и $AB$.
а) Докажите, что около четырёхугольника $BOCO_$ можно описать окружность.
б) Найдите площади четырёхугольников $BOCO_$ и $NOMO_$, если известно, что $AC=6$, $BC=8$, $AB=10$.

Задача по математике — 6827

Окружность с центром $O$ и окружность вдвое меньшего радиуса касаются внутренним образом в точке $A$. Хорда $AB$ большей окружности пересекает меньшую окружность в точке $M$.
а) Докажите, что $M$ — середина $AB$.
б) Луч $OM$ пересекает большую окружность в точке $P$. Найдите расстояние от центра большей окружности до хорды $AP$, если радиус большей окружности равен 13, а $OM=5$.

Задача по математике — 6828

Окружности с центрами $O_$ и $O_$ касаются внешним образом в точке $C$. К окружностям проведены общая внешняя касательная и общая внутренняя касательная. Эти касательные пересекаются в точке $D$.
а) Докажите, что треугольник $O_DO_$ прямоугольный.
б) Найдите радиусы окружностей, если известно, что $DO_=sqrt$ и $DO_=2sqrt$.

Задача по математике — 6829

В треугольник $ABC$ помещены две касающиеся окружности с центрами $O_$ и $O_$, причём первая из них касается сторон $AB$ и $AC$, а вторая — сторон $AB$ и $BC$.
а) Докажите, что прямые $AO_$ и $BO_$ пересекаются в центре окружности, вписанной в треугольник $ABC$.
б) Найдите радиусы окружностей, если известно, что они равны, а $AB=AC=10$ и $BC=12$.

Задача по математике — 6830

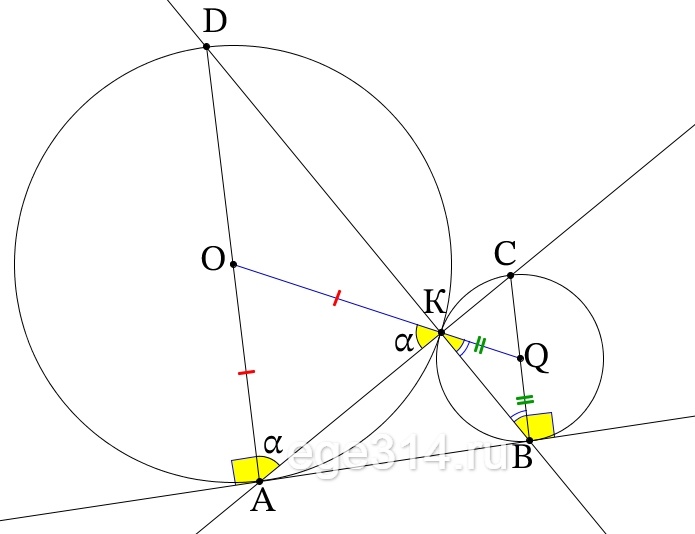
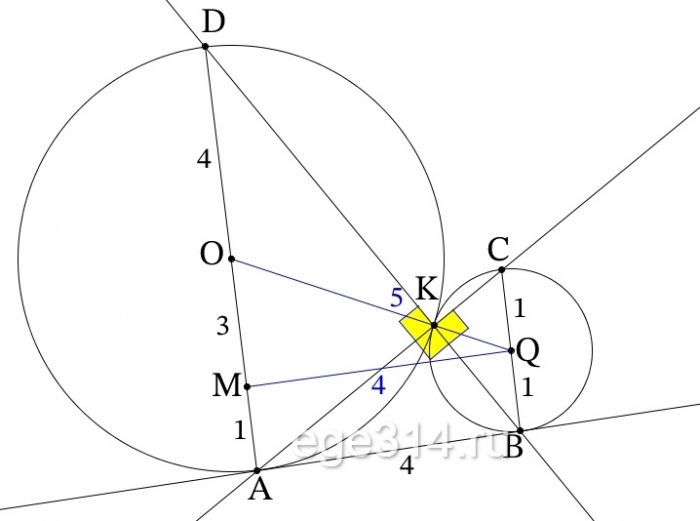
Две окружности касаются внешним образом в точке $K$. Прямая касается первой окружности в точке $A$, а второй — в точке $B$. Прямая $BK$ пересекает первую окружность в точке $D$, прямая $AK$ пересекает вторую окружность в точке $C$.
а) Докажите, что $ADparallel BC$.
б) Найдите площадь треугольника $DKC$, если известно, что радиусы окружностей равны 1 и 4.

Задача по математике — 6831

В равнобедренной трапеции $ABCD$ с основаниями $AD$ и $BC$ расположены две окружности, каждая из которых касается другой окружности, двух боковых сторон и одного из оснований. Пусть $P$ и $Q$ — точки касания окружностей с боковой стороной $AB$, а общая касательная окружностей, проходящая через их точку касания, пересекает боковые стороны в точках $M$ и $N$.
а) Докажите, что $MN=PQ$.
б) Найдите площадь трапеции $ABCD$, если известно, что $AD=18$ и $BC=2$.

Задача по математике — 6832

Окружности, построенные на сторонах $AB$ и $AC$ треугольника $ABC$ как на диаметрах, пересекаются в точке $D$, отличной от $A$.
а) Докажите, что точка $D$ лежит на прямой $BC$.
б) Найдите угол $BAC$, если известно, что $angle ACB=30^$, а точка $D$ лежит на стороне $BC$, причём $DB:DC=1:3$.

Задача по математике — 6833

Окружность с центром $O$ вписана в угол, равный $60^$. Окружность большего радиуса с центром $O_$ также вписана в этот угол и проходит через точку $O$.
а) Докажите, что радиус второй окружности вдвое больше радиуса первой.
б) Найдите длину общей хорды этих окружностей, если известно, что радиус первой окружности равен $2sqrt$.

Задача по математике — 6834

Две окружности пересекаются в точках $P$ и $Q$. Прямая, проходящая через точку $P$, второй раз пересекает первую окружность в точке $A$, а вторую — в точке $D$. Прямая, проходящая через точку $Q$ параллельно $AD$, второй раз пересекает первую окружность в точке $B$, а вторую — в точке $C$.
а) Докажите, что четырёхугольник $ABCD$ — параллелограмм.
б) Найдите отношение $BP:PC$, если радиус первой окружности вдвое больше радиуса второй.

Задача по математике — 6835

Окружности с центрами $O_$ и $O_$ разных радиусов пересекаются в точках $A$ и $B$. Хорда $AC$ большей окружности пересекает меньшую окружность в точке $M$ и делится этой точкой пополам.
а) Докажите, что проекция отрезка $O_O_$ на прямую $AC$ в четыре раза меньше $AC$.
б) Найдите $O_O_$, если известно, что радиусы окружностей равны 5 и 17, а $AC=16$.

Задача по математике — 6836

На диагоналях трапеции как на диаметрах построены окружности.
а) Докажите, что их общая хорда перпендикулярна основаниям трапеции.
б) Найдите длину этой хорды, если известно, что основания трапеции равны 1 и 11, а диагонали — 6 и 8.

Задача по математике — 6837

Две равные окружности с центрами $O_$ и $O_$ пересекаются в точках $M$ и $N$. Лучи $O_M$ и $O_N$ вторично пересекают окружность с центром $O_$ в точках $A$ и $B$ соответственно, причём $M$ — середина $O_A$.
а) Докажите, что точки $A$, $B$ и $O_$ лежат на одной прямой.
б) Окружности пересекают отрезок $O_O_$ в точках $C$ и $D$. Найдите отношение отрезка $CD$ к радиусу окружностей.

Видео:На окружности с центром O отмечены точки A и B так ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Решение №1957 Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй – в точке B.

Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй – в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

Источники: Демо 2022, Демо 2021, Демо 2020, Досрочная волна (Резерв) 2018, Демо 2019, Демо 2018, Демо 2017, Демо 2016, Демо 2015, Демо 2014

а)

ОА и QB радиусы к касательной АВ, значит ОА⊥АВ, QB⊥АВ, отсюда ОА||QB. Соединим центры окружностей ОQ, точка касания окружностей К∈ОQ.
ОАВQ – прямоугольная трапеция. Треугольник АОК равнобедренный, т.к. АО = ОК, как радиусы, углы при основании равны, обозначим их как α, ∠ОАК = ∠АКО = α, зная, что сумма углов треугольника равна 180°, найдём третий угол треугольника:

∠АОК = 180° – α – α = 180° – 2α

∠АОК и ∠ВQО углы при боковой стороны трапеции их сумма равна 180°, найдём ∠ВQО:

∠ВQО = 180 – (180° – 2α) = 180 – 180° + 2α = 2α

Треугольник КQB равнобедренный KQ = QB, как радиусы, углы при основании равны, найдём ∠QKB:

Угол ОКQ развёрнутый он равен 180°, состоит из трёх углов, найдём ∠АКВ:

∠АКВ = 180° – α – (90 – α) = 180° – α – 90° + α = 90°

∠АКВ = 90°, тогда ∠АКD тоже равен 90°, как смежный ему. Треугольник АКD прямоугольный, вписанный в окружность, значит АD – диаметр окружности с центром О.
∠АКD = ∠ВКС = 90°, как вертикальные, тогда ΔСКВ прямоугольный вписанный в окружность с центром Q, значит ВС – диаметр.
Т.к. радиусы ОА||QB, являющиеся частью диаметров АD и ВС, значит АD||ВС.
Что и требовалось доказать.
б) Проведём высоту QM прямоугольной трапеции, QM||AB, M∈DА.

QB = QK = 1, как радиусы меньшей окружности. ОК = ОА = 4, как радиусы большей окружности. Рассмотрим ΔОQM, он прямоугольный, ОQ = OK + KQ = 4 + 1 = 5, QB = MA = 1, как противоположные стороны прямоугольника. ОМ = ОА – МА = 4 – 1 = 3. Тогда MQ = 4, как сторона египетского треугольника (или по т.Пифагора). MQ = AB = 4, как противоположные стороны прямоугольника.
ΔАКD подобен ΔВСК (∠АКD = ∠ВКС = 90°, ∠АDK = ∠KBC, как накрестлежащие углы) с коэффициентом подобия:

Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.

Обозначим S_ΔBCK как S, тогда:

ΔАКD подобен ΔАКB (АК высота в прямоугольном ΔВАD, делит его на два подобных треугольника) с коэффициентом подобия:

Найдём S_ΔАВС:

S_ΔАKB = 4S, S_ΔBCK = S, тогда S_ΔABC = SΔАKB + S_ΔBCK = 4S + S = 5S:

S_ΔАKB = 4S = 4·0,8 = 3,2

🌟 Видео

Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

№639. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать

ЕГЭ задание 16Скачать

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Найдите угол АСО, если сторона СА касается окружностиСкачать

🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

№638. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать

Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать

НУ, ОЧЕНЬ КРАСИВЫЙ ОТВЕТ!Скачать

ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

№676. Стороны угла А касаются окружности с центром О радиуса r. Найдите: а) ОА,Скачать

Радиус окружности с центром в точке O равен 85 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать