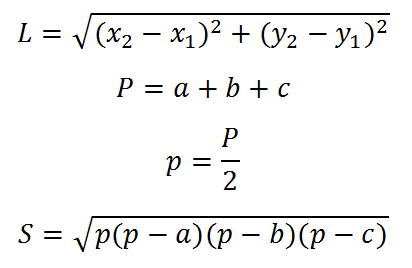Здравствуйте, дорогие читателинашего сайта. На этой недели счетчик посещаемости наконец-то сдвинулся с мертвой точки. Это не может не радовать. Если вы новоиспеченный постоянный посетитель этого сайта, оставьте комментарий к любому посту, чтобы мы не думали, что на нашем сайте обитают только боты 🙂 Ну что ж, приступим к решению задач Begin21-30.
Begin21. Даны координаты трех вершин треугольника: (x1, y1), (x2, y2), (x3, y3). Найти его периметр и площадь, используя формулу для расстояния между двумя точками на плоскости (см. задание Begin20). Для нахождения пло щади треугольника со сторонами a, b, c использовать формулу Герона: S = √(p ⋅ ( p − a) ⋅ ( p − b) ⋅ ( p − c)), где p — полупериметр.
На первый взгляд задача может показаться весьма и весьма трудной, и для того, чтобы не заблудиться в решении, составим план наших действий:
- Для того, чтобы найти периметр треугольника, находим расстояния между всеми вершинами (ведь расстояния между вершинами это и есть стороны) по формуле √((x2 — x1) 2 +(y2 — y1) 2 ), а затем суммируем их.
- Для того, чтобы найти площадь, используем формулу Герона.
Begin22°. Поменять местами содержимое переменных A и B и вывести новые значения A и B.
Эта классическая задача является основой более сложных алгоритмов. Представьте, у Вас есть два кувшина: первый наполнен водой, второй — соком. Требуется поменять жидкости местами, то есть, перелить воду во второй кувшин, а сок — в первый. Как Вы решите данную проблему? Скорее всего, Вы возьмете третий кувшин и временно перельете в него содержимое одного из кувшинов. Так и в Паскале: сначала мы присваиваем значение любой из двух переменных третьей, а уже потом перемещаем значения переменных.
Вода и персиковый сок
Begin23. Даны переменные A, B, C. Изменить их значения, переместив содер жимое A в B, B — в C, C — в A, и вывести новые значения переменных A, B, C.
И снова мы используем дополнительную переменную.
Begin24. Даны переменные A, B, C. Изменить их значения, переместив содержимое A в C, C — в B, B — в A, и вывести новые значения переменных A, B, C.
Задача, противоположная предыдущей.
Begin25. Найти значение функции y = 3·x 6 – 6·x 2 – 7 при данном значении x.
И снова мы прибегаем к помощи функций power и sqr .
Begin26. Найти значение функции y = 4·(x–3) 6 – 7·(x–3) 3 + 2 при данном значе нии x.
Begin27°. Дано число A. Вычислить A 8 , используя вспомогательную перемен ную и три операции умножения. Для этого последовательно находить A 2 , A 4 , A 8 . Вывести все найденные степени числа A.
В данной задачи требуется использовать вспомогательную переменную и три операции умножения, поэтому мы не можем использовать функцию power.
Begin28. Дано число A. Вычислить A 15 , используя две вспомогательные пере менные и пять операций умножения. Для этого последовательно находить A 2 , A 3 , A 5 , A 10 , A 15 . Вывести все найденные степени числа A.
Эта задача аналогична предыдущей, но немного сложнее .
Begin29. Дано значение угла α в градусах (0 этого же угла в радианах, учитывая, что 180° = π радианов. В качестве зна чения π использовать 3.14.
Две следующие задачи является актуальными для нас. Ведь функции sin, cos, arctan работают только с радианами. И программа, которая быстро переводит градусы в радианы или радианы в градусы, очень ценна. А теперь формула: Радианы = Градусы * pi / 180.
Begin30. Дано значение угла α в радианах (0 этого же угла в градусах, учитывая, что 180° = π радианов. В качестве зна чения π использовать 3.14.
Формула нахождения градусов следует из предыдущей формулы : Градусы = Радианы * 180 / pi. Кстати, в решении данной задачи я использую стандартное значение Pi = 3.14159265358979
На сегодня все! Мы с вами решили целых десять задач. Конечно, они не очень сложные, но ведь цель этих задач познакомить вас с основными функциями, вводом и выводом и показать вам то, как легко и интересно программировать на любом из языков программирования.
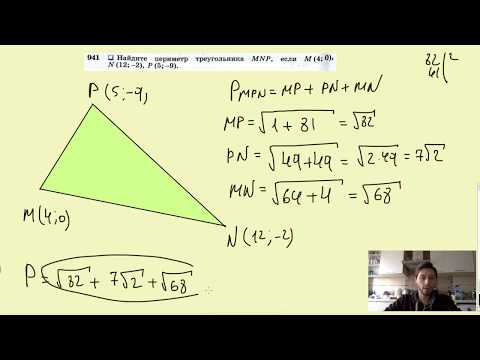
Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Заданы координаты трех вершин треугольника
Для решения данной задачи необходимо вспомнить формулы длины прямой, заданной координатами, периметра и полупериметра треугольника, а также площади треугольника по трем сторонам:
Формулы длины прямой по координатам, периметра, полупериметра и площади треугольника
Далее пишем простейшую программу:
Автор: Александр Чернышов
Оцените статью, это очень поможет развитию сайта.
Видео:Как найти площадь треугольника, зная координаты его вершины.Скачать

Периметр многоугольника по его координатам
| Координаты многоугольника, разделенные пробелами в формате x+iy | |
| Вы ввели следующие координаты многоугольника |
| Периметр многоугольника (в условных единицах) |