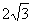- Ваш ответ
- решение вопроса
- Похожие вопросы
- Периметр треугольника АВС, описанного около окружности, равен 52 см?
- В треугольник с углами 50 и 70 вписана окружность?
- В треугольнике АВС биссектриса угла А делит высоту, проведенную из вершины В, в отношении 13 : 12, считая от точки В?
- В треугольнике АВС биссектриса угла А делит высоту, проведенную из вершины В, в отношении 13 : 12, считая от точки В?
- В треугольнике АВС биссектриса угла А делит высоту, проведенную из вершины В, в отношении 13 : 12, считая от т?
- Точка касания вписанной окружности делит сторону равностороннего треугольника на два отрезка?
- Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, проттиволежищей основанию?
- Вариант 4 № 23?
- Точки касания сторон треугольника с окружностью, вписанной в него, делят окружность на дуги в отношении 10 : 11 : 15?
- 1. Два угла треугольника равны 60 и 20 градусов?
- Боковая сторона равнобедренного треугольника, основание которого равно 6, делится точкой касания вписанной в него окружности в отношении 4 : 3, считая от вершины?
- Как найти периметр треугольника описанного около окружности
- Премиум
- Получи пятерку
- Как пользоваться?
- 📸 Видео
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Ваш ответ
Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

решение вопроса
Видео:Решение задачи №1 из ЕГЭ математикаСкачать
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,929
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Нафиг теорему синусов 3 задание проф. ЕГЭ по математике (часть I)Скачать

Периметр треугольника АВС, описанного около окружности, равен 52 см?
Геометрия | 5 — 9 классы
Периметр треугольника АВС, описанного около окружности, равен 52 см.
Т очка касания со стороной АВ делит эту сторону в отношении 2 : 3, считая от вершины А.
Точка касания со стороной ВС удалена от вершины С на 6 см.
Найдите стороны треугольника.
Помогиииииите плииииииииииииииииииииииз, пожалуйстаааааааааааа((((((((((.
Отрезки касательных к окружности, проведенные из одной точки, равны))).
Видео:Геометрия Радиус окружности описанной около треугольника ABC равен 6 см Найдите радиус окружностиСкачать

В треугольник с углами 50 и 70 вписана окружность?
В треугольник с углами 50 и 70 вписана окружность.
Найдите углы треугольника вершинами которого являются точки касания окружности со сторонами треугольника.
Видео:2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

В треугольнике АВС биссектриса угла А делит высоту, проведенную из вершины В, в отношении 13 : 12, считая от точки В?
В треугольнике АВС биссектриса угла А делит высоту, проведенную из вершины В, в отношении 13 : 12, считая от точки В.
Найдите длину стороны ВС треугольника, если радиус описанной около него окружности равен 26 см.
Видео:Задача 6 №27922 ЕГЭ по математике. Урок 139Скачать

В треугольнике АВС биссектриса угла А делит высоту, проведенную из вершины В, в отношении 13 : 12, считая от точки В?
В треугольнике АВС биссектриса угла А делит высоту, проведенную из вершины В, в отношении 13 : 12, считая от точки В.
Найдите длину стороны ВС треугольника, если радиус описанной около него окружности равен 26 см.
Видео:Задача 6 №27921 ЕГЭ по математике. Урок 138Скачать

В треугольнике АВС биссектриса угла А делит высоту, проведенную из вершины В, в отношении 13 : 12, считая от т?
В треугольнике АВС биссектриса угла А делит высоту, проведенную из вершины В, в отношении 13 : 12, считая от т.
В. Найдите длину стороны ВС треугольника, если радиус описанной около него окружности равен 26 см.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Точка касания вписанной окружности делит сторону равностороннего треугольника на два отрезка?
Точка касания вписанной окружности делит сторону равностороннего треугольника на два отрезка.
Один из которых на15 сантиметров меньше от периметра треугольника.
Найдите сторону треугольника.
Видео:Построить описанную окружность (Задача 1)Скачать

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, проттиволежищей основанию?
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 1, считая от вершины, проттиволежищей основанию.
Найдите периметр треугольника.
Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

Вариант 4 № 23?
В треугольнике АВС биссектриса угла А делит высоту проведенную из вершины В в отношении 13 : 12 считая от точки В .
Найдите длину стороны ВС треугольника если радиус описанной около него окружности равен 26см.
Видео:10 класс, 2 урок, Аксиомы стереометрииСкачать

Точки касания сторон треугольника с окружностью, вписанной в него, делят окружность на дуги в отношении 10 : 11 : 15?
Точки касания сторон треугольника с окружностью, вписанной в него, делят окружность на дуги в отношении 10 : 11 : 15.
Найдите углы этого треугольника.
Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

1. Два угла треугольника равны 60 и 20 градусов?
1. Два угла треугольника равны 60 и 20 градусов.
А) определите, в каком отношении вершины треугольника делят описанную окружность.
Б) найдите углы треугольника, вершинами которого являются точки касания вписанной окружности со сторонами данного треугольника.
Видео:№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать

Боковая сторона равнобедренного треугольника, основание которого равно 6, делится точкой касания вписанной в него окружности в отношении 4 : 3, считая от вершины?
Боковая сторона равнобедренного треугольника, основание которого равно 6, делится точкой касания вписанной в него окружности в отношении 4 : 3, считая от вершины.
Найдите периметр треугольника.
Вопрос Периметр треугольника АВС, описанного около окружности, равен 52 см?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Как найти периметр треугольника описанного около окружности
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.
Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.
Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:
Ты нашел то, что искал? Поделись с друзьями!
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.
По теореме синусов,
Получаем, что . Угол — тупой. Значит, он равен .
. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
Обучающее видео
БЕСПЛАТНО
Техническая поддержка:
help@ege-study.ru (круглосуточно)
Полный онлайн-курс подготовки к ЕГЭ по математике. Структурировано. Четко. Без воды. Сдай ЕГЭ на 100 баллов!
Для нормального функционирования и Вашего удобства, сайт использует файлы cookies. Это совершенно обычная практика.Продолжая использовать портал, Вы соглашаетесь с нашей Политикой конфиденциальности.
Все поля обязательны для заполнения
Видео:1 2 4 сопряжение окружностейСкачать

Премиум
Вся часть 2 на ЕГЭ по математике, от задачи 13 до задачи 19. То, о чем не рассказывают даже ваши репетиторы. Все приемы решения задач части 2. Оформление задач на экзамене. Десятки реальных задач ЕГЭ, от простых до самых сложных.
Видеокурс «Премиум» состоит из 7 курсов для освоения части 2 ЕГЭ по математике (задачи 13-19). Длительность каждого курса — от 3,5 до 4,5 часов.
- Уравнения (задача 13)
- Стереометрия (задача 14)
- Неравенства (задача 15)
- Геометрия (задача 16)
- Финансовая математика (задача 17)
- Параметры (задача 18)
- Нестандартная задача на числа и их свойства (задача 19).
Здесь то, чего нет в учебниках. Чего вам не расскажут в школе. Приемы, методы и секреты решения задач части 2.
Каждая тема разобрана с нуля. Десятки специально подобранных задач, каждая из которых помогает понять «подводные камни» и хитрости решения. Автор видеокурса Премиум — репетитор-профессионал Анна Малкова.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Получи пятерку
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Сразу после оплаты вы получите ссылки на скачивание видеокурсов и уникальные ключи к ним.
Задачи комплекта «Математические тренинги — 2019» непростые. В каждой – интересные хитрости, «подводные камни», полезные секреты.
Варианты составлены так, чтобы охватить все возможные сложные задачи, как первой, так и второй части ЕГЭ по математике.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Как пользоваться?
- Не надо сразу просматривать задачи (и решения) всех вариантов. Такое читерство вам только помешает. Берите по одному! Задачи решайте по однойи старайтесь довести до ответа.
- Если почти ничего не получилось – начинать надо не с решения вариантов, а с изучения математики. Вам помогут книга для подготовки к ЕГЭи Годовой Онлайн-курс.
- Если вы правильно решили из первого варианта Маттренингов 5-7 задач – значит, знаний не хватает. Смотри пункт 1: Книгаи Годовой Онлайн-курс!
- Обязательно разберите правильные решения. Посмотрите видеоразбор – в нем тоже много полезного.
- Можно решать самостоятельно или вместе с друзьями. Или всем классом. А потом смотреть видеоразбор варианта.
Стоимость комплекта «Математические тренинги – 2019» — всего 1100 рублей. За 5 вариантов с решениями и видеоразбором каждого.
Разделы: Математика
На итоговых уроках по геометрии времени на то, чтобы прорешать задачи по всему курсу в целом практически не остается. А в КИМы ЕГЭ традиционно включаются задачи, решение которых требует знаний планиметрии по теме «Вписанные и описанные окружности». Поэтому предложенный материал поможет не только вспомнить данную тему, но и систематизировать ранее полученные знания по решению планиметрических задач на вписанные и описанные окружности, а также подготовиться к решению подобных задач в ЕГЭ. При этом предполагается, что ученик хотя бы на минимальном уровне владеет всем курсом школьной геометрии (планиметрии).
Первым и важнейшим этапом решения геометрической задачи является построение чертежа. Нельзя научиться решать достаточно содержательные задачи, не выработав прочных навыков по изготовлению «хороших» чертежей, не выработав привычки (даже рефлекса) – не начинать решать задачу, пока не сделан «большой и красивый» чертеж. В качестве основного метода решения геометрических задач выдвигается алгебраический метод с составлением последующего алгоритма. Ставя во главу угла алгебраический метод, необходимо предостеречь от чрезмерного увлечения алгеброй и счетом, не забывать о том, что речь идет все же о геометрических задачах, а поэтому, работая над задачей, следует искать геометрические особенности, учиться смотреть и видеть геометрию. Выделив два слагаемых, определяющих умение решать геометрические задачи, – чертеж плюс метод, добавим сюда третье – владение определенными теоремами и опорными задачами, известными геометрическими фактами.
I. Необходимые теоремы и опорные задачи для окружности, вписанной в треугольник и четырехугольник, и окружности, описанной около треугольника и четырехугольника. (Приложение 1)
II. Решение задач по готовым чертежам (удобно воспользоваться кодоскопом).
При этом ученики устно объясняют ход решения задач, формулируют теоремы и опорные задачи, применяемые при решении задач по готовым чертежам.
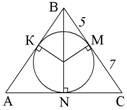
AB = BC = 12
MC = CN = 7, AC = 14, AK = AN = 7,
PABC = 12 + 12 + 14 = 38
Ответ: PABC = 38
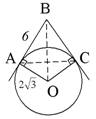
AB = 6,
АО =
1)
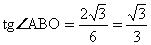 ,
, 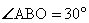
2) АВ = ВС,
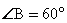 , т.к. ВО – биссектриса
, т.к. ВО – биссектриса 3)
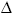 АВС – равносторонний, PABC = 6 • 3 = 18
АВС – равносторонний, PABC = 6 • 3 = 18 Ответ: PABC = 18
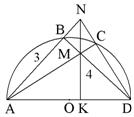
АВ = 3,
ВД = 4
1. Доказать: NM
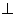 AD
AD 2. R = ?
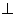 AN и AC
AN и AC 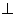 DN, т.е. AC и DB – высоты
DN, т.е. AC и DB – высоты 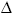 АND, тогда NK – высота, т.к. они пересекаются в одной точке.
АND, тогда NK – высота, т.к. они пересекаются в одной точке. Значит NM
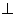 AD.
AD. 2. AD =
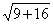 = 5, R =
= 5, R = 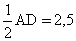
Ответ: R = 2,5
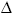 АВС, R =
АВС, R = 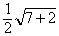 = 1,5
= 1,5 Ответ: R = 1,5
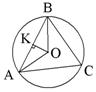
ОК = 5
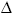 .
. 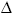 BKO – прямоугольный, ВК = AK = 12,
BKO – прямоугольный, ВК = AK = 12, КО = 5, ВО =
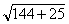 = 13 = R
= 13 = R Ответ: R = 13
III. Решение задач.
1. Найти периметр прямоугольного треугольника, если радиус вписанной окружности 2 см, а гипотенуза 13 см.
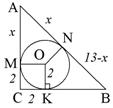 | Пусть AM = AN = x, тогда AC = x + 2, CB = 2 + 13 – x = 15 – x (x + 2) 2 + (15 – x) 2 = 169 x 2 – 13x + 30 = 0 x1 = 10, x2 = 3; AC = 6, CB = 12; P = 30 см Ответ: P = 30 см. |
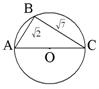
2. Радиус вписанной в прямоугольный треугольник окружности 3 см, О – центр вписанной окружности, 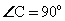
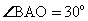
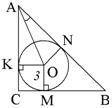 | АО – биссектриса,  AKO – прямоугольный, AKO – прямоугольный, sin 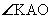 = sin 30 о = = sin 30 о = 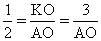 , АО = 6, , АО = 6, AN = AK = 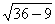 = 3 = 3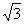 , AC = 3 + 3 , AC = 3 + 3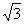 , , tg 60 о = 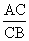 , CB = , CB =  SABC = 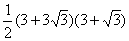 = = 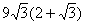 Ответ: S = 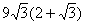 см2. см2. |
3. Периметр треугольника 84. Точка касания вписанной окружности делит одну из сторон на отрезки 12 и 14. Найти радиус вписанной окружности и площадь 
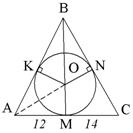 | P = 84, KB = BN = 16, ON = 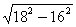 = = 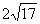 = r = r AB = 28, BC = 30, AC = 26 По формуле Герона: SABC = 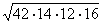 = 336 = 336 Ответ: r = 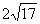 ; S = 336. ; S = 336. |
4. В равнобедренном треугольнике расстояние от центра вписанной окружности до вершины не равного угла 5 см. Большая сторона 10 см. Найти радиус вписанной окружности.
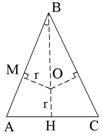 | OB = 5, 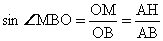 , , OM = OB . 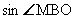 = =  , BH = 5 + r, , BH = 5 + r, AH = 2r, 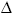 AHB – прямоугольный, AHB – прямоугольный,  4r 2 = 100 – (5 + r) 2 , r 2 + 2r – 15 = 0, r1 = – 5, r2 = 3 Ответ: r = 3 см. |
5. Основание равнобедренного треугольника, вписанного в окружность радиуса 5 см, равно 6 см. Найти периметр треугольника.
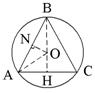 | 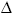 AHO – прямоугольный: OH = 4, BH = 4 + 5 =9, AHO – прямоугольный: OH = 4, BH = 4 + 5 =9, AB = BC = 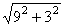 = = 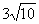 P = 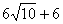 Ответ: P = 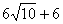 см. см. |
6. Периметр треугольника АВС равен 72 см. AB = BC, AB:AC = 13:10. Найти радиус описанной около треугольника окружности.
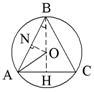 | AB + BC + AC = 72, 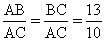 , , 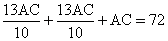 AC = 20, AB = BC = 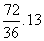 = 26, BH = = 26, BH = 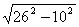 = 24 = 24 BN = NA = 13, 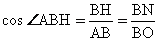 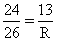 , R = , R = 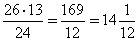 Ответ: R = 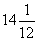 см. см. |
7. Основание тупоугольного равнобедренного треугольника равно 24 см, а радиус описанной окружности 13 см. Найти боковую сторону треугольника.
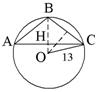 | OC = 13, AC = 24, HC = 12 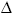 HOC – прямоугольный, OH = HOC – прямоугольный, OH = 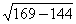 = 5 = 5 BH = BO – OH =13 – 5 = 8 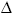 BHC – прямоугольный, BC = BHC – прямоугольный, BC = 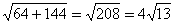 Ответ: 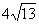 см. см. |
8. Окружность, диаметром которой служит АС треугольника АВС, проходит через точку пересечения медиан этого треугольника. Найти отношение длины стороны АС к длине проведенной к ней медианы.
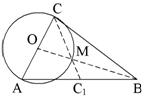 | AO = OC = R = OM, BM = 2R, BO = 3R, 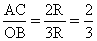 Ответ: 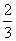 . . |
9. Найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
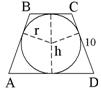 | SABCD = 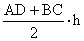 Т.к. окружность вписанная, то AB + CD = AD + BC = 20 h = 2r = 8, 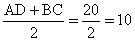 , SABCD = 10 • 8 = 80 , SABCD = 10 • 8 = 80 Ответ: 80. |
10. Дан ромб ABCD. Окружность, описанная около треугольника ABD, пересекает большую диагональ ромба AC в точке E. Найдите CE, если AB = 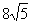
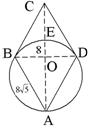 | 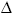 AOB – прямоугольный: AO = AOB – прямоугольный: AO = 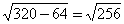 = 16 = 16 AD = 32 По теореме об отрезках пересекающихся хорд: BO • OD = AO • OE, 8 • 8 = 16 • OE, OE = 4, CE = 16 – 4 = 12 Ответ: 12. |
IV. Задачи для самостоятельного решения.
1. Радиус окружности, вписанной в прямоугольный треугольник, равен 2 см, а радиус описанной окружности равен 5 см. Найдите больший катет треугольника.
2. Около равнобедренного треугольника с основанием АС и углом при основании 75о описана окружность с центром О. Найдите ее радиус, если площадь треугольника ВОС равна 16.
3. Найдите радиус окружности, вписанной в остроугольный треугольник АВС, если высота BH равна 12 и известно, что 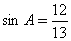
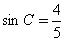
4. Один из катетов прямоугольного треугольника равен 15, а проекция второго катета на гипотенузу равна 16. Найдите диаметр окружности, описанной около этого треугольника.
5. В равнобедренный треугольник АВС вписана окружность. Параллельно его основанию АС проведена касательная к окружности, пересекающая боковые стороны в точках D и E. Найдите радиус окружности, если DE = 8, AC = 18.
6. Около треугольника ABC описана окружность. Медиана треугольника AM продлена до пересечения с окружностью в точке K. Найдите сторону AC, если AM= 18, MK = 8, BK = 10.
7. Окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.
8. Угол В треугольника АВС равен 60 о , радиус окружности, описанной около АВС, равен 2. Найти радиус окружности, проходящей через точки А и С и центр окружности, вписанной в АВС.
9. Стороны треугольника равны 5, 6 и 7. Найти отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.
10. Радиус окружности, вписанной в прямоугольный треугольник, равен полуразности его катетов. Найти отношение большего катета к меньшему.
Ответ: (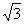
11. Диагонали четырехугольника ABCD, вписанного в окружность, пересекаются в точке М, прямые AB и CD пересекаются в точке N. Известно, что 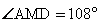
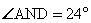
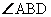
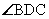
12. Высоты AH и BK остроугольного треугольника ABC пересекаются в точке M, 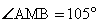
13. Около окружности описана равнобочная трапеция с основаниями 5 и 3. Найти радиус окружности.
Ответ: (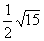
14. В равнобедренный 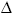
15. Дан прямоугольный треугольник ABC с прямым углом C. Через центр O вписанной в треугольник окружности проведен луч BO, пересекающий катет AC в точке M. Известно, что AM = 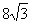
Окружность вписана в треугольник. В данной статье собрал для вас задачи, в которых даётся треугольник с вписанной в него или описанной около него окружностью. В условии ставится вопрос о нахождении радиуса окружности или стороны треугольника.
Данные задания удобно решать используя представленные формулы. Рекомендую их выучить, бывают очень полезны не только при решении этого типа заданий. Одна формула выражает связь радиуса вписанной в треугольник окружности с его сторонами и площадью, другая радиус описанной около треугольника окружности также с его сторонами и площадью:
где a, b, c – стороны треугольника
S – площадь треугольника
27900. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120 0 . Найдите диаметр описанной окружности этого треугольника.
Здесь окружность описана около треугольника.
Диаметр мы сможем найти, если будет известен радиус. Используем формулу радиуса описанной около треугольника окружности:
где a, b, c – стороны треугольника
S – площадь треугольника
Две стороны нам известны (боковые стороны равнобедренного треугольника), третью мы можем вычислить используя теорему косинусов:
Теперь вычислим площадь треугольника:
*Использовали формулу (2) из этой статьи .
Таким образом диаметр будет равен 2.
Это устные вычисления. Для тех кто имеет навык решения заданий с вписанным в окружность шестиугольником, тот сразу определит, что стороны треугольника АС и ВС «совпадают» со сторонами вписанного в окружность шестиугольника (угол шестиугольника как раз равен 120 0 , как и в условии задачи). А далее на основании того, что сторона вписанного в окружность шестиугольника равна радиусу этой окружности не сложно сделать вывод о том, что диаметр будет равен 2АС, то есть двум.
Подробнее о шестиугольнике посмотрите информацию в этой статье (п.5).
Воспользуемся формулой радиуса окружности вписанной в треугольник:
где a, b, c – стороны треугольника
S – площадь треугольника
Нам неизвестны ни стороны треугольника, ни его площадь. Обозначим катеты как х, тогда гипотенуза будет равна:
А площадь треугольника будет равна 0,5х 2 .
Таким образом, гипотенуза будет равна:
В ответе требуется записать:
Воспользуемся формулой радиуса окружности вписанной в треугольник:
где a, b, c – стороны треугольника
S – площадь треугольника
Две стороны известны (это катеты), можем вычислить третью (гипотенузу), также можем вычислить и площадь.
По теореме Пифагора:
Воспользуемся формулой радиуса окружности вписанной в треугольник:
где a, b, c – стороны треугольника
S – площадь треугольника
Известны все стороны, вычислим и площадь. Её мы можем найти по формуле Герона:
27624. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
27625. Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.
27626. Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.
27923. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.
27932. Катеты равнобедренного прямоугольного треугольника равны 
Если в условии дан треугольник и вписанная или описанная окружность, и речь идёт о сторонах, площади, радиусе, то сразу вспомните об указанных формулах и пробуйте использовать их при решении. Если не получается, то тогда уже ищите другие способы решения.
📸 Видео
Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

ЕГЭ математика 2023 Вариант 2 задача 1Скачать