Пересечение цилиндра с треугольникам (8 видео)

Инженерная графика

Содержание

Пересечение поверхностей геометрических тел
Линии пересечения и перехода
Построение линии пересечения тел методом секущих плоскостей
Взаимное пересечение поверхностей тел с примерами и образцами выполнения
Пересечение прямой линии с поверхностями тел
Линии пересечения и перехода
Общие правила построения линий пересечения поверхностей
Пересечение поверхностей цилиндра и призмы
Пересечение цилиндрических поверхностей
Пересечение поверхностей многогранников
Пересечение поверхностей цилиндра и конуса
Пересечение поверхностей сферы и цилиндра
Пересечение поверхностей тора и цилиндра
Построение линий пересечения поверхностей способом вспомогательных сфер
Взаимное пересечение поверхностей геометрических тел
ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
ГЕОМЕТРИЧЕСКИХ ТЕЛ
Учебное пособие
💡 Видео

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Пересечение поверхностей геометрических тел

Линии пересечения и перехода

В предыдущей статье рассмотрены методы построения линий пересечения поверхностей многогранных геометрических тел, при этом опорные точки таких линий лежат на ребрах и гранях, что позволяет достаточно легко определить позицию проекций точек на том или ином виде.

Детали, составляющие различные технические конструкции, нередко имеют сложную форму, в которой можно выделить сочетание геометрических тел – цилиндра, конуса, сферы, а также различных тел, содержащих плоские грани. Пересекаясь определенным образом, эти тела образуют общую линию, принадлежащую их поверхностям, которая называется линией пересечения.
На чертежах линии пересечения поверхностей изображаются сплошной основной линией.

Линии пересечении поверхностей некоторых тел, например — литых или штампованных деталей, невозможно показать на чертеже четко из-за плавного перехода одной поверхности в другую. В этом случае воображаемая линия пересечения указывается на чертеже сплошной тонкой линией, которая начинается и заканчивается в точках пересечения продолжения контура взаимно пересекающихся поверхностей.

Встречаются и детали, имеющие всевозможные линии пересечения и перехода поверхностей. Особенно много линий перехода бывает у деталей, изготовленных литьем.

Построение линий пересечения и перехода поверхностей при выполнении чертежей различных технических деталей требует знания основных приемов начертательной геометрии, применяемых при взаимном пересечении поверхностей геометрических тел.
Для нахождения линий пересечения геометрических тел наиболее часто используют способ секущих плоскостей , а в некоторых случаях – способ вспомогательных сфер.

При выполнении машиностроительных чертежей наиболее часто встречаются случаи пересечения двух цилиндрических поверхностей, а также поверхностей многогранников, цилиндра и конуса, сферы с цилиндром, многогранником или конусом.

Построение линии пересечения тел методом секущих плоскостей

Этот метод заключается в проведении вспомогательных секущих плоскостей через взаимно пересекающиеся геометрические тела, и нахождении общих точек, составляющих линию пересечения поверхностей данных геометрических тел. Построение линии пересечения поверхностей тел начинают с нахождения очевидных точек.
Например, на рис. 1, где изображены линии пересечения призмы с конусом, такими точками являются точки А и В.

Затем определяют характерные точки, расположенные, например, на очерковых образующих поверхностей вращения или крайних ребрах, отделяющих видимую часть линий перехода от невидимой. На рис. 1 это точки С и D. Они располагаются на крайних ребрах верхней горизонтальной грани призмы.

Все остальные точки линии пересечения называются промежуточными (например, точки Е и F на рис. 1). Обычно для их определения используют вспомогательные параллельные секущие плоскости (рис. 1, а).

В качестве вспомогательных плоскостей выбирают такие плоскости, которые пересекают обе заданные поверхности по простым линиям – прямым или окружностям, причем окружности должны располагаться в плоскостях, параллельных плоскостям проекций.

В примере, показанном на рис. 1, в, плоскость Р рассекает конус по окружности, с помощью которой находят горизонтальные проекции точек e и f.

Во всех случаях перед тем, как строить линию пересечения поверхностей на чертеже, необходимо представить себе эту линию в пространстве (рис. 1, б).

На рисунках 2 и 4 показаны примеры построения линии пересечения треугольной призмы и цилиндра, а также конуса и цилиндра с помощью вспомогательных горизонтальных секущих плоскостей.
На рисунках 3 и 5 показаны примеры построения линии пересечения двух цилиндров, а также цилиндра и тора с использованием вспомогательных вертикальных секущих плоскостей.

Видео:Задание 54. Аксонометрия ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 2Скачать

Взаимное пересечение поверхностей тел с примерами и образцами выполнения

Содержание:

Взаимное пересечение поверхностей. Поверхности могут взаимно пересекаться. При этом линии одной поверхности пересекаются с другой поверхностью и образуют точки, которые в совокупности представляют линию пересечения.

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Пересечение прямой линии с поверхностями тел

Конструкции деталей можно рассматривать как сочетание различных геометрических тел. Необходимо уметь строить линии пересечения поверхностей этих тел. Пример, где требуется подобное построение, показан на рис. 195, на котором изображен бункер, ограниченный цилиндрической поверхностью А, пересекающейся с конической поверхностью Б и поверхностью пирамиды В.

В зависимости от вида поверхностей тел линии пересечения могут быть лекальными кривыми или ломаными.

Для решения задач на построение линий пересечения поверхностей необходимо предварительно усвоить построение точек пересечения прямой с поверхностями различных геометрических тел.

Если прямая пересекается с поверхностью тела, получаются две точки, одновременно принадлежащие как поверхности тела, так и прямой линии. Такие точки называются точками входа и выхода (рис. 196. а; точки N и М). Для нахождения этих точек выполняются построения в следующем порядке.

Через данную прямую проводят вспомогательную плоскость (обычно проецирующую). Например, на рис. 196, а, где изображено пересечение прямой АВ с поверхностью пирамиды, через прямую проведена вспомогательная горизонтально-проецирующая плоскость Р. Затем находят линии пересечения вспомогательной плоскости с поверхностью данного геометрического тела (линии КС и ЕD). На пересечении полученных линий с заданной прямом находят искомые точки (точки N и М).

На комплексном чертеже точки входа и выхода определяют следующим образом (рис. 196. б). Горизонтальные проекции kс и ed прямых КС и ED совпадают с горизонтальным следом плоскости Р_H. Фронтальные проекции точек k‘, с’, е’ и d‘ определяют, пользуясь вертикальными линиями связи, проведенными из точек k, с, е и d до пересечения с фронтальными проекциями основания пирамиды. Соединяют точки k‘ с с’ и е’ с d‘ прямыми. На пересечении фронтальных проекций найденных прямых с проекцией а’Ь’ данной прямой получают фронтальные проекции n‘ и т’ искомых точек входа и выхода. Проведя через них вертикальные линии связи, находят горизонтальные проекции п и т этих точек.

В некоторых частных случаях можно обойтись без применения вспомогательной плоскости. Например, точки входа и выхода прямой АВ с поверхностью прямого кругового цилиндра (рис. 197, а) определяют следующим образом.

Горизонтальная проекция цилиндрической поверхности представляет собой окружность, поэтому горизонтальные проекции всех точек, расположенных на цилиндрической поверхности, в том числе и двух искомых точек, будут расположены на этой окружности (рис. 197, а).

Фронтальные проекции n‘ и m‘ искомых точек определяют, проводя через точки n и m вертикальные линии связи до встречи с данной фронтальной проекцией а’Ь’ прямой АВ.

На рис. 197, б, в показано построение точек входа и выхода прямой АВ и поверхности прямого кругового конуса. Через прямую АВ проводят вспомогательную плоскость Р, проходящую через вершину конуса. Плоскость Р пересечет конус по образующим SH₃ SH_4.

На комплексном чертеже изображение плоскости Р строят следующим образом. На прямой АВ берут произвольную точку К и соединяют ее с вершиной S конуса прямой линией. Две пересекающиеся прямые АВ и SK определяют плоскость Р.

Чтобы найти точки входа и выхода, необходимо построить горизонтальные проекции образующих SH₃ и SH₄. Для этого продолжим s’k’ и а’b‘ до пересечения с осью х в точках h‘₂ и h‘₁. Опустим линию связи из точки k‘ до пересечения с ab, полученную точку k соединим с s. Продлим горизонтальную проекцию прямой SK до пересечения с линией связи, опушенной из точки h‘₂, получим точку h₂. Из точки h‘₁ проведем линию связи до пересечения с продолжением прямой ab, получим точку h₁. Через следы h₁ и h₂ пройдет горизонтальный след плоскости Р. Точки h₁ и h₂ соединим прямой и получим горизонтальный след Р_Н плоскости Р.

Основание конуса является горизонтальным следом конической поверхности. Поэтому, определив точки пересечения этого следа со следом Р_Н плоскости Р, можно найти и те две образующие, по которым коническая поверхность пересекается вспомогательной плоскостью Р. На комплексном чертеже горизонтальная проекция основания конуса (окружность) пересекается со следом Р_Н в точках h₃ и h₄. Эти точки соединяют с вершиной s и получают следы sh₃ и sh₄ образующих SH₃ и SH₄.

На пересечении найденных образующих с данной прямой АВ находят искомые точки М и N — точки входа и выхода прямой АВ с конической поверхностью.

Горизонтальные проекции точек т и n находят на пересечении горизонтальных проекций образующих sh₃ и sh₄ с горизонтальной проекцией прямой ab. Через точки m и n проводят вертикальные линии связи до пересечения а’b‘ и находят фронтальные проекции т‘ и n‘ точек входа и выхода.

Точки входа и выхода прямой АВ с поверхностью сферы (рис. 198) находят, проведя через прямую АВ вспомогательную фронтально-проецирующую плоскость Р.

Вспомогательная плоскость Р пересекает сферу по окружности, которая проецируется на плоскость Н в виде эллипса, что затрудняет построение. Поэтому в данном случае необходимо применить способ перемены плоскостей проекций. Новую плоскость проекций выбирают так, чтобы вспомогательная плоскость Р была бы ей параллельна, т.с. следует провести новую ось проекций x₁ так. чтобы она была параллельна фронтальной проекции а’b‘ прямой АВ (для упрощения построении на рис. 198 ось x₁ проведена через проекцию а’b‘).

Затем необходимо построить новую горизонтальную проекцию a₁b₁ прямой АВ и новую горизонтальную проекцию окружности диаметра D, по которой плоскость Р пересекает сферу. На пересечении новых горизонтальных проекций двух искомых точек m_> и n_> Обратным построением определяем фронтальные т’ и n‘ и горизонтальные т и п проекции точек входа и выхода.

Видео:85КБ. Пересечение поверхностей цилиндра и полусферы. Определение видимости.Скачать

Линии пересечения и перехода

Многие детали машин представляют собой конструкции из пересекающихся геометрических тел. Общая линия пересекающихся поверхностей называется линией пересечения.

На чертежах линии пересечения поверхностей изображаются сплошной основной линией (рис. 199, а). В местах перехода поверхностей литых и штампованных деталей нет четкой линии пересечения. Воображаемая линия пересечения называется линией перехода и условно изображается на чертежах сплошной тонкой линией. Эта линия начинается и заканчивается в точках пересечения продолжения контура взаимно пересекающихся поверхностей (рис. 199. б).

Встречаются детали, имеющие всевозможные линии пересечения и перехода поверхностей. Особенно много линий перехода у поверхностей деталей, изготовленных литьем.

На рис. 200, а на приборе для испытания твердости видны линии переходов различных поверхностей.

Кожух и крышка смесительного аппарата (рис. 200. б) имеют разнообразные линии перехода. Здесь можно видеть линии взаимного пересечения цилиндрических и других поверхностей.

Построение линий пересечения и перехода поверхностей при выполнении чертежей трубопроводов, вентиляционных устройств, резервуаров, кожухов машин, станков требует точности.

Видео:Построение линии пересечения поверхности цилиндра с проецирующей плоскостиСкачать

Общие правила построения линий пересечения поверхностей

Метод построения линий пересечения поверхностей тел заключается в проведении вспомогательных секущих плоскостей и нахождении отдельных точек линий пересечения данных поверхностей в этих плоскостях.

Построение линии пересечения поверхностей тел начинают с нахождения очевидных точек. Например, на рис. 201, где изображены линии пересечения призмы с конусом, такими точками являются точки А и В. Затем определяют характерные точки, расположенные, например, на очерковых образующих поверхностей вращения или крайних ребрах, отделяющих видимую часть линий перехода от невидимой. На рис. 201 это точки С и D. Они располагаются на крайних ребрах верхней горизонтальной грани призмы.

Все остальные точки линии пересечения называются промежуточными (например, точки Е и F). Обычно их определяют с помощью вспомогательных параллельных секущих плоскостей (рис. 201, а).

В качестве вспомогательных плоскостей выбирают такие плоскости, которые пересекают обе заданные поверхности по простым линиям — прямым или окружностям, причем окружности должны располагаться в плоскостях, параллельных плоскостям проекций.

В данном примере плоскость Р рассекает конус по окружности (рис. 201, в), с помощью которой находят горизонтальные проекции точек е и f.

Во всех случаях. перед тем как строить линию пересечения поверхностей на чертеже, необходимо представить себе эту линию в пространстве (рис. 201, б).

Видео:Задание 54. Чертеж ЛИНИИ ПЕРЕСЕЧЕНИЯ цилиндра и призмы трехгранной Часть 1Скачать

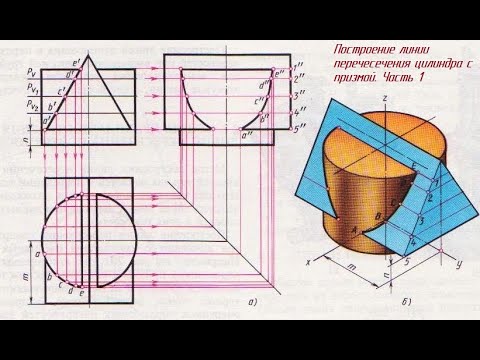
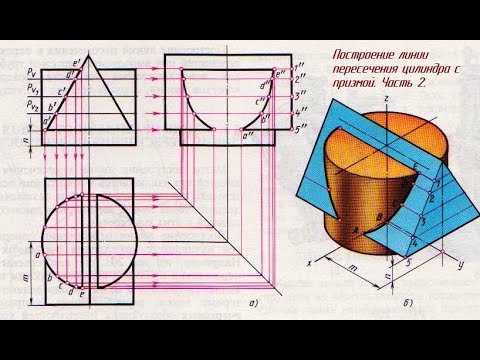
Пересечение поверхностей цилиндра и призмы

На рис. 202 показано построение проекции линий пересечения поверхности треугольной призмы с поверхностью прямого кругового цилиндра. Боковые грани призмы перпендикулярны плоскости V (рис. 202, а), поэтому фронтальная проекция линий пересечения поверхностей этих тел совпадает с фронтальной проекцией основания призмы. Горизонтальные проекции линий пересечения поверхностей совпадают с горизонтальной проекцией цилиндра и являются окружностью. Профильные проекции точек А и Е находим по горизонтальным и фронтальным проекциям с помощью линий связи. Для построения проекций промежуточных точек В, С, D используем вспомогательные секущие плоскости Р_V, Р_V1 и Р_V2, c помощью которых находим фронтальные проекции b‘, с’. d‘ точек B, С. D.

В данном примере можно обойтись без вспомогательных секущих плоскостей, намечая произвольно на фронтальной проекции точки b‘, с’, d‘.

Опуская линии связи на горизонтальную проекцию, находим горизонтальные проекции с, Ь, d точек С, В, D. На профильной проекции с помощью линий связи находим проекции Ь», с”, d«.

На рис. 202, б показано построение изометрической проекции. После построения изометрической проекции цилиндра, используя размеры т и п (рис. 202, а), строят изометрическую проекцию основания призмы, на котором находят точки 1, 2. 3. 4. 5. От этих точек откладывают расстояния 1«е». 2“d« и т.п., взятые с профильной проекции комплексного чертежа, и находят точки А, В. С, D. Е

На изометрической проекции линия пересечения поверхностей цилиндра и призмы получается соединением точек А, В. С, D, Е, которые строятся но координатам, взятым с комплексного чертежа.

Видео:Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

Пересечение цилиндрических поверхностей

При выполнении машиностроительных чертежей наиболее часто встречается случай пересечения двух цилиндрических поверхностей, оси которых расположены под углом 90 0 .

Разберем пример построения линии пересечения поверхностей двух прямых круговых цилиндров. оси которых перпендикулярны к плоскостям проекций (рис. 203, а).

В начале построения, как известно, находим проекции очевидных точек 1, 7 и 4.

Построение проекций промежуточных точек показано на рис. 203, б. Если в данном примере применить общий способ построения линий пересечения с помощью вспомогательных взаимно параллельных плоскостей, пересекающих обе цилиндрические поверхности по образующим, то на пересечении этих образующих будут найдены искомые промежуточные точки линии пересечения (например, точки 2, 3, 5 на рис. 203, а). Однако в данном случае выполнять такое построение нет необходимости по следующим соображениям.

Горизонтальная проекция искомой линии пересечения поверхностей совпадает с окружностью — горизонтальной проекцией большого цилиндра. Профильная проекция линии пересечения также совпадает с окружностью — профильной проекцией малого цилиндра. Таким образом, фронтальную проекцию искомой линии пересечения легко найти по общему правилу построения кривой линии по точкам, когда две проекции точек известны. Например, по горизонтальной проекции точки 3 (рис. 203, б) находят профильную проекцию 3″. Но двум проекциям 3 и 3″ определяют фронтальную проекцию 3′ точки 3. принадлежащей линии пересечения цилиндров.

Построение изометрической проекции пересекающихся цилиндров начинают с построения изометрической проекции вертикального цилиндра. Далее через точку а₁ параллельно оси х проводят ось горизонтального цилиндра. Положение точки О₁ определяется величиной h₁, взятой с комплексного чертежа (рис. 203, б). Отрезок, равный h, откладываем от точки О вверх по оси z (рис. 203, в). Откладывая от точки О₁ по оси горизонтального цилиндра отрезок l, получим точку О₂ — центр основания горизонтального цилиндра.

Изометрическая проекция линии пересечения поверхностей строится по точкам с помощью трех координат. Однако в данном примере искомые точки можно построить иначе.

Так, например, точки 3 и 2 строят следующим образом. От центра О₂ (рис. 203, в) вверх, параллельно оси z, откладывают отрезки т и п, взятые с комплексного чертежа. Через концы этих отрезков прямые, параллельные оси у, до пересечения с основанием горизонтального цилиндра в точках 3₁ и 2₁. Затем из точек 1. 3 проводят прямые, параллельные оси х, и на них откладывают отрезки, равные расстоянию от основания горизонтального цилиндра до линии пересечения, взятые с фронтальной или горизонтальной проекции комплексного чертежа. Конечные точки этих отрезков будут принадлежать линии пересечения. Через полученные точки проводят по лекалу кривую, выделяя се видимые и невидимые части.

Пример взаимного пересечения цилиндрических поверхностей с осями, перпендикулярными друг к другу, приведен на рис. 204, а. Одна цилиндрическая поверхность корпуса имеет вертикальную ось, а другая (половина цилиндра) — горизонтальную.

Если диаметры пересекающихся цилиндрических поверхностей одинаковы. то профильная проекция линии пересечения представляет собой две пересекающиеся прямые (рис. 204, б).

Если пересекающиеся цилиндрические поверхности имеют оси, расположенные под углом, отличным от прямого угла, то линию их пересечения строят с помощью вспомогательных секущих плоскостей или другими способами (например, способом сфер).

Видео:Задание 50. Построение ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ЦИЛИНДРОВСкачать

Пересечение поверхностей многогранников

При пересечении двух многогранников линия пересечения поверхностей представляет собой ломаную линию.

Если ребра двух призм взаимно перпендикулярны (рис. 205, а), то линия пересечения призм строится следующим образом.

Горизонтальная и профильная проекции линии пересечения совпадают соответственно с горизонтальной проекцией пятиугольника (основания одной призмы) и с профильной проекцией четырехугольника (основания другой призмы). Фронтальную проекцию ломаной линии пересечения строят по точкам пересечения ребер одной призмы с гранями другой.

Например, взяв горизонтальную 1 и профильную 1″ проекции точки 1 пересечения ребра пятиугольной призмы с гранью четырехугольной (рис. 205, а) и пользуясь известным приемом построения, с помощью линии связи можно легко найти фронтальную проекцию 1′ точки 1, принадлежащей линии пересечения призм.

Изометрическая проекция двух пересекающихся призм (рис. 205, б) может быть построена по координатам соответствующих точек.

Например, изометрическую проекцию двух точек 5 и 5₁, симметрично расположенных на левой грани пятиугольной призмы, строят так. Принимая для удобства построений за начало координат точку О, лежащую на верхнем основании пятиугольной призмы, откладываем влево от О по оси х отрезок ОЕ, величину которого берут с комплексного чертежа на фронтальной или горизонтальной проекции. Далее из точки Е вниз параллельно оси z откладываем отрезок EF, равный а, и, наконец, от точки F влево и вправо параллельно оси у откладываем отрезки F5 и F5_1, равные с/2.

Далее от точки F параллельно оси х откладываем отрезок n, взятый с комплексного чертежа. Через его конец проводим прямую, параллельную оси у, и откладываем на ней отрезок, равный с. Вниз параллельно оси z откладываем отрезок, равный Ь, и параллельно у — отрезок, равный k. В результате получаем изометрию основания четырехугольной призмы.

Точки 1 и 4 на ребрах пятиугольной призмы можно построить, используя только одну координату z.

Примеры, где требуются подобные построения, показаны на рис. 206, на которых видны линии пересечения поверхностей призм.

Линию пересечения поверхностей четырехугольной призмы с четырехугольной пирамидой (рис. 207, а) строят по точкам пересечения ребер одного многогранника с гранями другого многогранника.

Например, проекции точек 1 и 3 искомой линии пересечения находят следующим образом. Фронтальные проекции 1‘ и 3′ очевидны. Профильные проекции 1“ и 3“ и горизонтальные 1 и 3 находят с помощью линий связи. Аналогично находят точки 2 и 4.

На рис. 207, б и в показана последовательность построения диметрической проекции. Сначала строят пирамиду. Для построения призмы от точки О откладывают отрезок ОО₁, взятый с фронтальной проекции комплексного чертежа (О’ О’₁ ). и получают точку О₁ (рис. 207, б). Через точку О₁ проводят параллельно оси х ось симметрии призмы и по ней от точки откладывают вправо и влево половины высоты призмы. Через точки О₂ и О₃ проводят прямые, параллельные осям у и z, на которых откладывают соответственно половину и целую длину диагоналей четырехугольника основания призмы. Соединив концы диагоналей прямыми, получают диметрическую проекцию основания призмы.

Диметрические проекции точек пересечения 2. 4, б. 8 ребер призмы и пирамиды получаются без дополнительных построений (рис. 207, в).

Диметрические проекции точек пересечения 1, 3, 5. 7 ребер пирамиды с гранями призмы находят по координатам известным способом.

В этом примере диметрические проекции точек 1, 3, 5 и 7 можно построить иначе. От середины левого основания призмы — точки О₂ — откладываем вверх и вниз по оси z соответственно отрезки т и n, взятые с комплексного чертежа. Через концы отрезков т и n проводят прямые, параллельные оси у, до пересечения с контуром основания призмы в точках А, В, С и D. Через эти точки проводят прямые, параллельные оси х, до пересечения с ребрами пирамиды. В результате получают искомые точки 1, 3, 5 и 7.

На рис. 208 показан корпус оптического компаратора, который имеет элементы пересечения поверхностей пирамид и призм. На рисунке видна линия пересечения поверхностей этих тел.

Видео:Линия пересечения плоскостейСкачать

Пересечение поверхностей цилиндра и конуса

Пример пересечения поверхностей цилиндра и конуса показан на рис. 209, б. Построение линии пересечения поверхностей прямого кругового усеченного конуса, имеющего вертикальную ось, с цилиндром, расположенным горизонтально, показано на рис. 209, а. Оси цилиндра и конуса пересекаются в точке О₁ и лежат в одной плоскости.

Как и ранее, сначала определяют проекции очевидных 1, 7 и характерных 4, 10 точек линии пересечения.

Для определения промежуточных точек проводят вспомогательные горизонтальные секущие плоскости Р₁…Р₅. (рис. 209, а). Они будут рассекать конус по окружности, а цилиндр по образующим (рис. 209, б). Искомые точки линии пересечения находятся на пересечении образующих с окружностями.

Для определения горизонтальных проекций точек пересечения из центра O₁ проводят горизонтальные проекции дуг окружностей (рис. 209, а), по которым вспомогательные плоскости Р₁…Р₅ пересекают конус. Размеры радиусов этих дуг окружностей взяты с профильной проекции.

Так как профильные проекции точек 1“… 12“ известны, то, проводя линии связи до пересечения с соответствующими дугами окружностей, находят горизонтальные проекции точек 1… 12. Используя линии связи, по двум имеющимся проекциям, профильной и горизонтальней, находим фронтальные проекции точек пересечения 1‘. 12’.

Полученные на фронтальной и горизонтальной проекциях точки, принадлежащие к линии пересечения. обводят по лекалу.

На горизонтальной проекции часть линии пересечения будет видимой, а часть — невидимой. Границу этих частей линии пересечения определяют с помощью вспомогательной секущей плоскости Р₃, проведенной через ось цилиндра. Точки, расположенные над плоскостью Р₃ (см. профильную проекцию), будут на плоскости Н видимы, а точки, расположенные под плоскостью Р₃_,— невидимы.

Изометрическую проекцию пересекающихся поверхностей цилиндра и конуса вычерчивают в такой последовательности. Вначале выполняют изометрическую проекцию конуса (рис. 209, в). Затем от центра О нижнего основания конуса по его оси вверх откладывают координату ОО₁ = h и получают точку О₁, через которую проводят ось цилиндра параллельно изометрической оси х. От точки О₁ по этой оси откладывают координату х = О₁О₂ точки О₂ — центра окружности основания цилиндра.

Для построения линии пересечения находят изометрические проекции точек этой линии с помощью их координат, взятых с комплексного чертежа. За начало координат принимается точка О₂ (центр основания цилиндра). Параллельно оси у проводят до пересечения с овалом следы плоскостей сечения с координатами по оси z, взятых с профильной проекции. Из полученных точек А, В, С. параллельно оси х проводят прямые — образующие цилиндра, на них откладывают координаты Al, В2, . взятые с фронтальной проекции комплексного чертежа, и получают точки 2. 12, принадлежащие искомой линии пересечения.

Через найденные точки проводят кривую линию по лекалу.

На рис. 210 показана деталь. Линию пересечения конической поверхности с цилиндрической строят описанным выше способом.

Построение линии пересечения поверхностей цилиндра и конуса, оси которых параллельны (рис. 211), аналогично построению, рассмотренному на рис. 209.

Выбирают вспомогательные горизонтальные плоскости, например Р₁, Р₂ и Р₃, которые пересекают конус и цилиндр по окружностям (рис. 211, б). Диаметр окружностей, образованных в результате пересечения этих плоскостей с цилиндрам, одинаков и равен D; диаметры окружностей, полученных в результате пересечения плоскостей с конусом, — различные. Взаимное пересечение горизонтальных проекций этих окружностей дают искомые горизонтальные проекции точек 1. 9 линии пересечения (рис. 211, а). Фронтальные проекции 1′. 9′ этих точек находят с помощью линий связи на фронтальных следах Р_V1, Р_V₂, Р_V₃вспомогательных плоскостей. Профильные проекции точек строят по двум их известным проекциям.

Характерными точками в данном примере являются: высшая точка линии пересечения — точка 5, нахождение проекций которой начинают с имеющейся горизонтальной проекции, и точки 1, 9

Точки 1 и 9 получились от пересечения оснований цилиндра и конуса.

Построение изометрической проекции пересекающихся конуса и цилиндра (рис. 211, в) выполняется по этапам, подробно описанным в предыдущем примере (см. рис. 209, в). Построение начинается проведением изометрических осей конуса и цилиндра, затем их оснований (эллипсов) с центрами на расстоянии друг от друга, определяемом координатой n₃. Для построения линий пересечения находят изометрические проекции точек этой линии с помощью координат, взятых с чертежа.

На рис. 212 показана деталь, имеющая форму двух цилиндров, пересекающихся с конусом. Оси цилиндра и конуса параллельны.

Примеры пересечения поверхностей даны на рис. 213. Линии пересечения показаны красным цветом.

Видео:Задание 51. Как начертить ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПРИЗМ.Скачать

Пересечение поверхностей сферы и цилиндра

Прямой круговой цилиндр, расположенный перпендикулярно плоскости Н, пересекается с шаром, центр которого расположен на оси цилиндра, по окружности, которая изображается на фронтальной проекции отрезком прямой (рис 214). Проводя через точки А и В пересечения контурных образующих цилиндра и очерка шара вспомогательную горизонтальную плоскость Р, заметим следующее. Плоскость Р пересечет как цилиндр, так и шар по окружности одинакового диаметра, которая расположена в проецирующей плоскости. Следовательно, се фронтальная проекция будет изображаться в виде прямой а’b’.

При пересечении поверхности конуса или поверхности вращения с шаром, центр которого расположен на оси этих поверхностей, также получается окружность (рис. 214, а).

Если центр шара расположен вне оси цилиндра (рис. 214, б), то для построения линии пересечения применяют вспомогательные горизонтальные плоскости. Например, вспомогательная горизонтальная плоскость Р пересекает цилиндр по окружности радиуса r, а шар — по окружности радиуса R. Точки пересечения а и b горизонтальных проекций этих окружностей принадлежат горизонтальной проекции линии пересечения. Фронтальные проекции а’ и b‘ строят, используя линии связи.

Одной из характерных точек данной линии пересечения является верхняя точка D. Горизонтальная проекция этой точки находится на пересечении прямой, соединяющей центры окружностей радиусов r и R с горизонтальной проекцией основания цилиндрической поверхности. Для построения фронтальной проекции точки D через точку d проводят дугу радиуса r₁, строят фронтальную проекцию дуги (отрезок прямой, параллельной оси х) и с помощью линии связи находят точку d’.

Видео:РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Пересечение поверхностей тора и цилиндра

Патрубок, форма которого образована пересекающимися поверхностями тора и цилиндра, показан на рис. 215. Выполнен комплексный чертеж с построением линии пересечения поверхностей и тора, и цилиндра. В этом примере очевидные точки 1 и 5. Для определения проекций промежуточных точек используют вспомогательные плоскости Р_Н и P_Н1, параллельные фронтальной плоскости проекции. Например, плоскость Р_Н пересекает поверхность тора по окружности радиуса R, а поверхность цилиндра — по двум образующим Взаимное пересечение этих образующих с дугою окружности радиуса R дает на фронтальной проекции две точки 2′ и 4′, принадлежащие искомой линии пересечения.

Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Построение линий пересечения поверхностей способом вспомогательных сфер

Для построения линии пересечения поверхностей вместо вспомогательных секущих плоскостей при определенных условиях удобно применять вспомогательные сферические поверхности.

В отличие от метода вспомогательных секущих плоскостей метод вспомогательных сфер имеет преимущество, так как при построении фронтальной проекции линии пересечения поверхностей не используются две другие проекции пересекающихся поверхностей (рис. 216).

Вспомогательные сферические поверхности для построения линий пересечения поверхностей тел можно применять лишь при следующих условиях:

а) пересекающиеся поверхности должны быть поверхностями вращения;

б) оси поверхностей вращения должны пересекаться; точка пересечения осей является центром вспомогательных сфер;

в) оси поверхностей вращения должны быть параллельны какой-либо плоскости проекций.

Примеры применения вспомогательных сферических поверхностей показаны на рис. 216, а и б.

На рис. 216, а дано построение фронтальных проекций линии пересечения поверхностей двух цилиндров, оси которых пересекаются под острым углом.

Вспомогательные сферические поверхности проводят из точки О’ пересечения осей цилиндров.

Построим, например, фронтальную проекцию некоторой промежуточной точки линии пересечения. Для этого из точки О’ проводят сферическую поверхность радиуса R, которая на данной проекции изобразится в виде окружности этого же радиуса. Окружность радиуса R пересечет горизонтальный цилиндр по окружностям диаметра АС и ВD, а наклонно расположенный цилиндр — по окружностям диаметра АВ.

В пересечении полученных проекций окружностей — отрезков а’b’ и c‘d‘— находят проекцию 2′ промежуточной точки линии пересечения.

Вводя еще целый ряд вспомогательных сферических поверхностей, можно построить необходимое число точек линии пересечения.

Пределы радиусов сферических поверхностей находят следующим образом (рис. 216, а и б): наибольшая окружность сферической поверхности должна пересекаться с контурными образующими 1—1 и II— II цилиндра и наименьшая должна быть касательной к одной из данных пересекающихся поверхностей и пересекаться с образующими другой поверхности.

Если поверхности двух конусов (рис. 217, а) описаны около шара, то они касаются шара по двум окружностям; эти окружности пересекаются в двух точках, которые проецируются на фронтальную плоскость проекций в точку р’. Плоскости, в которых лежат эти окружности, пересекаются по прямой, соединяющей точки пересечения линий касания конусов с шаром. Окружности проецируются на фронтальную плоскость проекций в виде прямых линий.

Соединив очевидную точку s’ пересечения конусов с точкой р‘, получим линию пересечения конусов с шаром, которая представляет собой фронтальную проекцию эллипса.

Разберем второй подобный пример. Если два прямых круговых цилиндра с осями, пересекающимися в точке О’ (рис. 217, б), описаны около шара с центром в точке О, то фронтальная проекция шара будет окружностью, касательной к контурным образующим цилиндров. Линии пересечения поверхностей этих цилиндров представляют собой эллипсы, фронтальные проекции которых изображаются в виде прямых линий а’b‘ и c’d’.

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Как начертить цилиндр в объемеСкачать

Взаимное пересечение поверхностей геометрических тел

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)

ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО УНИВЕРСИТЕТА

Допущено учебно-методическим объединением Совета директоров средних специальных учебных заведений Волгоградской области в качестве учебного пособия для образовательных учреждений среднего профессионального образования Волгоградской области

Рецензенты: директор филиала Камышинские электрические сети, к. т. н. ; преподаватель высшей квалификационной категории Камышинского технического колледжа

Деманова пересечение поверхностей геометрических тел: Учеб. пособие / ВолгГТУ, Волгоград, 2007. – 32 с.

Содержит теоретические основы способов построения линии пересечения поверхностей и примеры построения линии пересечения поверхностей различными способами. На рисунках к каждой задаче изометрическая проекция и наглядная модель позволяют облегчить понимание изложенного материала для построения линии пересечения.

Предназначено для студентов всех форм обучения специальностей 1004 (ОКСО 140212) «Электроснабжение (по отраслям)», 1201 (ОКСО 151001) «Технология машиностроения», 2802 (ОКСО 260704) «Технология текстильных изделий».

Ил. 11. Библиогр.: 4 назв.

Печатается по решению редакционно-издательского совета

Волгоградского государственного технического университета

ISBN -4 © Волгоградский

университет, 2007

На чертежах линии пересечения поверхностей изображаются сплошной основной линией, которая строится по точкам пересечения элементарных геометрических тел.

Способы определения точек линии пересечения элементарных геометрических тел изложены в данном учебном пособии.

Существует воображаемая линия пересечения, которая называется линией перехода и условно изображается сплошной тонкой линией. Эта линия начинается и заканчивается в точках пересечения продолжения контура взаимно пересекающихся поверхностей литых и штампованных деталей.

В машиностроении встречаются детали, имеющие всевозможные линии пересечения и перехода поверхностей.

1. линии пересечения поверхностей

Конструкцию деталей можно рассматривать как сочетание различных геометрических тел. Необходимо уметь строить линии пересечения этих тел. Например, на рис. 1 изображен бункер, ограниченный цилиндрической поверхностью А, пересекающийся с конической поверхностью Б и поверхностью пирамиды В.

В зависимости от вида поверхностей тел линии могут быть лекальными, кривыми или ломаными.

При пересечении поверхности тел можно получить: 1) полное пересечение (проницание), в этом случае линия пересечения представляет собой два замкнутых контура (рис. 9, 10, 11); 2) неполное пересечение (врезка), когда линия пересечения представляет собой один замкнутый контур (рис. 2, 3, 4, 5).

Для построения линии пересечения используют два метода: метод вспомогательных секущих плоскостей и метод вспомогательных сфер.

2. ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ СПОСОБОМ ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХ ПЛОСКОСТЕЙ

2.1. Общие положения

Построение линии пересечения поверхностей начинают с очевидных точек. Например, на рис. 2, где изображена линия пересечения призмы с конусом, такими точками являются точки А и В. Затем определяют характерные точки, расположенные, например, на очерковых образующих поверхностей вращения или крайних ребрах, определяющих видимую и невидимую части линии пересечения. На рисунке это точки С и D. Они располагаются на верхней горизонтальной грани призмы.

Все остальные точки называются промежуточными. Обычно их определяют методом вспомогательных секущих плоскостей.

Последовательность построения линий пересечения этим методом следующая:

· выбирают вид вспомогательных плоскостей;

· строят линию пересечения вспомогательных плоскостей с заданными поверхностями;

· находят точки пересечения построенных линий и соединяют их между собой.

Вспомогательные секущие плоскости должны быть параллельны между собой и пересекать обе заданные поверхности по простым линиям: прямым и окружностям, причем окружности должны располагаться в плоскостях, параллельных плоскости проекций. В примере на рис. 2а плоскость Р рассекает конус по окружности, а призму – по прямым линиям.

Рис. 2б показывает изометрическую проекцию, а рис. 2в – ортогональный чертеж пересекающихся тел. Построение очевидных точек А и В начинаем с фронтальной проекции, точек С и D – с профильной проекции, а промежуточные точки Е и F получаем посредством вспомогательной плоскости уровня – плоскости Р (рис. 2в).

2.2. Примеры построения линии пересечения поверхностей

вращения с применением секущих плоскостей

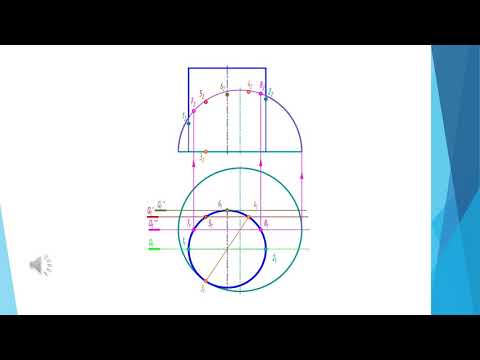
2.2.1. Пересечение поверхностей цилиндра и призмы

На рис. 3 показано построение проекции линии пересечения поверхности треугольной призмы с поверхностью прямого кругового цилиндра. Боковые грани призмы перпендикулярны плоскости проекций V (рис. 3а), поэтому фронтальная проекция линии пересечения поверхностей этих тел совпадает с фронтальной проекцией боковых граней призмы. Горизонтальная проекция линии пересечения поверхностей совпадает с горизонтальной проекцией цилиндра и является окружностью. Профильные проекции точек А и Е находим по горизонтальным и фронтальным проекциям при помощи линий связи. Для построения проекций промежуточных точек В, С, D используем вспомогательные секущие плоскости Рv, Рv1 и Рv2, которые рассекают поверхность цилиндра по окружности, а поверхность призмы по прямым линиям. Окружности и прямые, пересекаясь между собой, дают точки В, С и D.

В данном примере можно обойтись без вспомогательных секущих плоскостей, помечая произвольно на фронтальной проекции линии пересечения точек b¢, c¢, d¢. Опуская линии связи на горизонтальную проекцию, находим горизонтальные проекции точек b, c, d.

На рис. 3б показано построение изометрической проекции. После построения изометрической проекции цилиндра, используя размеры m и n, строят изометрическую проекцию основания призмы, а затем достраивают ее до конца. На рис. 3а изображена модель пересекающихся тел и определены точки линии пересечения с применением секущих плоскостей.

Точки А, В, С, D, Е и им симметричные точки строятся по координатам, взятым с комплексного чертежа. Соединяются точки линии пересечения с помощью лекала.

2.2.2. Пресечение цилиндрических поверхностей

При выполнении машиностроительных чертежей наиболее часто встречается случай пересечения двух цилиндрических поверхностей, оси которых взаимно перпендикулярны.

На рис. 4 показано построение линии пересечения поверхностей двух прямых круговых цилиндров, оси которых перпендикулярны к плоскостям проекций.

В начале построения, как известно, находят проекции очевидных точек 1, 7 и 4 .

Построение проекций промежуточных точек показано на рис. 4а. Если в данном случае принять общий способ построения линии пересечения с помощью вспомогательных взаимно параллельных плоскостей, пересекающих обе цилиндрические поверхности по образующим, то на пересечении этих образующих будут найдены искомые промежуточные точки линии пересечения: точки 2, 3, 5.

Однако в данном случае выполнять такое построение нет необходи-

мости по следующим соображениям.

Горизонтальная проекция линии пересечения поверхностей совпадает с окружностью – горизонтальной проекцией большого цилиндра. Профильная проекция линии пересечения также совпадает с окружностью – профильной проекцией малого цилиндра. Таким образом, фронтальную проекцию искомой линии пересечения легко найти по общему правилу построения кривой линии по точкам, когда две проекции точек известны (рис. 4б).

Например, по горизонтальной проекции точки 3 находят профильную проекцию 3². По двум проекциям 3 и 3² определяют фронтальную проекцию 3¢. Полученные точки соединяют плавной кривой с помощью лекала.

Построение изометрической проекции (рис. 4в) пересекающихся цилиндров выполняется в следующей последовательности:

строят изометрическую проекцию вертикального цилиндра;

О1

О2

строят основание горизонтального цилиндра – овал, параллельный профильной плоскости проекций;

строят точки, принадлежащие линии пересечения при, помощи координат и соединяют их, используя лекало;

проводят очерковые образующие горизонтального цилиндра.

2.2.3. Пресечение поверхностей цилиндра и конуса

Построение линии пересечения поверхностей прямого кругового усеченного конуса, имеющего вертикальную ось, с цилиндром, расположенным горизонтально, показано на рис. 5. Оси цилиндров и конуса пересекаются в точке О1 и лежат в одной плоскости.

Как и в предыдущих примерах, сначала определяют проекции очевидных (1, 7) и характерных (4, 10) точек линии пересечения.

Для определения промежуточных точек проводят вспомогательные горизонтальные секущие плоскости Р1… Р5 (рис. 5б). Они будут рассекать конус по окружности, цилиндр – по образующим. Искомые точки линии пересечения поверхностей цилиндра и конуса находятся на пересечении образующих с окружностями.

Для определения горизонтальных проекций точек пересечения из центра О1 (рис. 5а) проводят горизонтальные проекции дуг окружностей, по которым вспомогательные плоскости Р1… Р5 пересекают конус. Размеры радиусов этих дуг взяты с профильной проекции.

Так как профильные проекции точек 1²… 12″ известны, то проводя ломаные линии связи до пересечения с соответствующими дугами окружностей, находят горизонтальные проекции точек 1…12. Применяя линии связи по двум имеющимся проекциям, профильной и горизонтальной, находят фронтальные проекции точек 1¢… 12′.

Полученные на горизонтальной и фронтальной проекциях точки соединяют по лекалу.

На горизонтальной проекции часть линии пересечения будет видимой, а часть – невидимой. Границу этих частей линии пересечения определяют при помощи плоскости Р3, проведенной через ось цилиндра. Точки, расположенные над плоскостью Р3, будут на горизонтальной плоскости видимы, а точки расположенные под плоскостью Р3 – невидимы.

Изометрическую проекцию пересекающихся поверхностей цилиндра и конуса вычерчивают в такой же последовательности, что и изометрическую проекцию пересекающихся поверхностей цилиндров (рис. 5в).

На рис. 6 показано построение линии пересечения поверхностей цилиндра и конуса, оси которых параллельны.

В качестве вспомогательных секущих плоскостей выбирают горизонтальные плоскости, которые пересекают конус и цилиндр по окружностям (рис. 6б). Диаметр окружностей, образованных в результате пересечения этих плоскостей с цилиндром, одинаков и равен D; диаметры окружностей, полученных от пересечения плоскостей с поверхностью конуса, различны. Взаимное пересечение горизонтальных проекций этих окружностей дает искомые горизонтальные проекции точек 1 … 9 линии пересечения. Фронтальные проекции точек 1¢… 9¢ (рис. 6а) находят при помощи линий связи на следах Рv1, Рv2, Рv3 вспомогательных плоскостей. Профильные проекции точек строят по двум их известным проекциям.

Характерными точками в данном примере являются: высшая точка линии пересечения (точка 5) и низшие точки (1 и 9). Построение проекций этих точек начинается с имеющихся горизонтальных проекций.

Построение изометрической проекции пересекающихся конуса и цилиндра (рис. 6в) выполняется по этапам, описанным в предыдущих примерах.

2.2.4. Пересечение поверхностей тора и цилиндра

Пересечение поверхностей тора и цилиндра показано на рис. 7. Комплексный чертеж пересекающихся поверхностей с построением линии пересечения выполнен на рис. 7а.

В этом примере очевидные точки К и S, характерные – L и Р. Для определения проекций промежуточных точек используют вспомогательные плоскости Рv1, Рv2, Рv3, параллельные фронтальной плоскости проекций.

Вспомогательная плоскость (например Р2) пересекает поверхность тора по окружности радиуса R, а поверхность цилиндра – по двум образующим M и N. Пересечение этих образующих с окружностью радиуса R дает две точки m и n, принадлежащие искомой линии пересечения. Наглядное изображение линии пересечения дано на рис. 7б.

Рис. 7.

3. ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ СПОСОБОМ

3.1. Общие положения

Известно, что если ось поверхности вращения проходит через центр сферы и сфера пересекает эту поверхность, то линия пересечения сферы и поверхности вращения – окружность, плоскость которой перпендикулярна оси поверхности вращения. При этом, если ось поверхности вращения параллельна плоскости проекций, то линия пересечения на эту плоскость проецируется в отрезок прямой линии. На рис. 8 показана фронтальная проекция пересечения сферой радиуса R поверхностей вращения – конуса, тора, цилиндра, сферы, оси которых проходят через центр сферы радиуса R и параллельны фронтальной плоскости. Окружности, по которым пересекаются указанные поверхности с поверхностью сферы, проецируются на фронтальную плоскость в виде отрезков прямых. Это свойство используют для построения линии взаимного пересечения двух поверхностей вращения с помощью вспомогательных сфер.

В данном пособии рассмотрен способ вспомогательных концентрических сфер с постоянным центром – сфер с постоянным центром.

Способ секущих сфер с постоянным центром применяют при следующих условиях:

обе пересекающиеся поверхности – поверхности вращения;

· оси поверхностей вращения пересекаются, точку пересечения принимают за центр вспомогательных концентрических сфер;

· оси поверхностей вращения должены быть параллельны одной из плоскостей проекций.

3.2. Примеры построения линии пересечения поверхностей

вращения способом вспомогательных сферических поверхностей

3.2.1. Пересечение двух цилиндров, цилиндра и усеченного конуса

На рис. 9а дано построение фронтальной проекцией линии пересечения поверхностей двух цилиндров, оси которых пересекаются под острым углом.

Вспомогательные сферические поверхности проводятся из точки пересечения осей цилиндров, точки О¢.

Построим, например, фронтальную проекцию некоторой промежуточной точки. Для этого из точки О¢ проведём сферическую поверхность радиуса R, которая на данной проекции изобразится окружностью того же радиуса. Окружность радиуса R пересекает горизонтальный цилиндр по окружностям диаметра СD, а наклонно расположенный цилиндр – по окружностям диаметра АВ.

Пересекаясь между собой, проекции окружностей, отрезки с¢d¢ и a¢b¢ дают проекцию 2¢ промежуточной точки линии пересечения.

Пределы радиусов сферических поверхностей находят следующим образом: наибольшая окружность сферической поверхности должна пересекаться с контурными образующими I-I и II-II, а наименьшая должна быть касательной к одной из данных поверхностей и пересекаться с образующими другой поверхности.

На рис. 9б при помощи сфер с постоянным центром аналогично предыдущему примеру построена фронтальная проекция линии пересечения усеченного конуса и горизонтального цилиндра.

4. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ МНОГОГРАННИКОВ

4.1. Общие положения

В общем случае линия пересечения поверхностей многогранников представляет собой пространственную замкнутую ломаную линию, которая в некоторых частных случаях может оказаться плоской.

Построение линии пересечения поверхностей двух многогранников сводится к построению точки пересечения ребер одного многогранника с ребрами или гранями другого.

4.2. Примеры построения линии пересечения многогранников

4.2.1. Пересечение поверхностей призм

В рассматриваемом примере ребра призм взаимно перпендикулярны (рис. 10). Горизонтальная и профильная проекции линии пересечения совпадают соответственно с горизонтальной проекцией пятиугольной призмы и с профильной проекцией части четырехугольной призмы. Фронтальную проекцию ломаной линии пересечения строят по точкам пересечения ребер одной призмы с гранями другой.

Например, взяв горизонтальную 1 и профильную 1² проекции точки 1 пересечения ребра пятиугольной призмы с гранью четырехугольной и пользуясь известным приемом построения, с помощью линий связи можно легко найти фронтальную проекцию 1¢ точки 1 (рис. 10а).

Изометрическая проекция двух пересекающихся призм (рис. 10б) строится в следующей последовательности:

· Строят изометрическую проекцию вертикальной призмы.

· Строят изометрическую проекцию линии пересечения, используя координаты точек, принимая за начало координат точку О, лежащую на верхнем основании пятиугольной призмы.

· Строят основание четырехугольной призмы. Для этого от точки F параллельно оси х откладывают отрезок n, взятый с комплексного чертежа. Через его конец проводят прямую, параллельную оси y и откладывают на ней отрезок С. Вниз параллельно оси z откладывают отрезок, равный К.

· Параллельно оси у проводят видимые части боковых ребер четырехугольной призмы.

· Соединяют концы боковых ребер, проводят видимые ребра второго основания четырехугольной призмы.

4.2.2 Пересечение поверхностей призмы и пирамиды

Построение линии пересечения поверхностей четырехугольной призмы и четырехугольной пирамиды показано на рис. 11.

Фронтальная проекция линии пересечения совпадает с проекцией призмы.

Горизонтальную и профильную проекции линии пересечения строят по точкам пересечения ребер одного многогранника с ребрами или гранями другого (рис. 11а).

Точки 1, 3, 5 и 7 являются точками пересечения боковых ребер пирамиды с боковыми гранями призмы. Фронтальные проекции их очевидны, горизонтальные и профильные проекции этих точек находятся на соответствующих проекциях ребер пирамиды.

Точки 2, 4, 6 и 8 являются точками пересечения ребер пирамиды с ребрами призмы. Фронтальные и профильные проекции их очевидны, горизонтальные проекции находят на пересечении линий связи.

Последовательность построения аксонометрической (диметрической) проекции следующая (рис. 11б):

· Строят диметрическую проекцию пирамиды.

· Строят основание призмы. Для этого с помощью координат z и х строят точки О1 и О3, проводя прямые параллельные у и z, на которых откладывают соответственно половину и целую длину диагонали четырехугольника, основания призмы. Концы диагоналей соединяют.

· Строят диметрическую проекцию линии пересечения. Диметрические проекции точек пересечения ребер призмы и пирамиды 2, 4, 6, 8 получаются без дополнительных построений (рис. 11б). Диметрические проекции точек 1, 3, 5, 7 строят по их координатам (рис. 11в).

Рис. 11.

5. СОДЕРЖАНИЕ ГРАФИЧЕСКОЙ РАБОТЫ

Выполнить ортогональный чертеж пересекающихся тел в трех проекциях. Показать все вспомогательные построения тонкими линиями. Обозначить все точки линии пересечения. Показать и обозначить вспомогательные секущие плоскости. Выполнить аксонометрическую (диметрическую или изометрическую) проекцию пересекающихся тел с нанесением точек линии пересечения.

6. ОФОРМЛЕНИЕ ГРАФИЧЕСКОЙ РАБОТЫ

Б.

А.

7. ПОРЯДОК ВЫПОЛНЕНИЯ

Ознакомиться с рекомендуемой литературой, а также соответствующим разделом данного пособия. Распланировать изображения чертежа по габаритным размерам, оставляя место для выполнения изометрической проекции.

8. ВАРИАНТЫ ЗАДАНИЙ

В соответствии с приложением Б.

9. КОНТРОЛЬНЫЕ ВОПРОСЫ

Как располагаются виды на комплексном чертеже? В виде каких фигур проецируются основные геометрические тела: цилиндр, конус, шар, куб, призма и пирамида? Какова последовательность построения линии пересечения тел? В какой последовательности определяют три проекции точки, заданной на поверхности предмета одной из своих проекций? Как строится вспомогательная прямая на чертеже? В чем состоит суть способа вспомогательных секущих плоскостей? Когда его применяют? В чем состоит суть способа вспомогательных секущих сфер? Когда его применяют? Когда не требуется дополнительных построений для определения точек линии пересечения? В каких случаях поверхности вращения пересекаются по плоским кривым линиям?

10. Список использованной ЛИТЕРАТУРы

1. , Миронов графика: Учебник. – 2-е изд., испр. и доп. – М.: ВШ; Издательский центр «Академия», 2001. – 288 с.

2. , Миронов заданий по инженерной графике: Учеб. пособие. – 2-е изд., испр. – М.: ВШ; Изд. центр «Академия», 2000. – 263 с.

3. Боголюбов : Учебник для средних специальных учебных заведений. – 2-е изд., испр. – М.: Машиностроение, 1989. – 336 с.

4. Лагерь графика: Учебник. – М.: ВШ, 2003. – 272 с.